Professional Documents
Culture Documents
Chapter 5 Applications of Definite Integral: 5-1 Area Between Curves
Uploaded by
Afiqah ZainuddinOriginal Description:
Original Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Chapter 5 Applications of Definite Integral: 5-1 Area Between Curves
Uploaded by
Afiqah ZainuddinCopyright:
Available Formats
1
dx
Chapter 5 Applications of Definite Integral
5-1 Area between Curves:
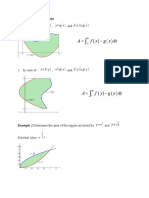
Let ) (x f y = and ) (x g y = are continuous functions such that ) ( ) ( x g x f for all x in the interval
] , [ b a . Then the area A bounded by the two curves ) (x f , ) (x g and the two lines a x = , b x = is given
by
) (x f y
top
=
= = =
b
a
bot top
b
a
dx y y dx x g x f dA A ] [ )] ( ) ( [ dA
where
= dA The area element dx y y
bot top
] [ =
The last formula can be interpreted as a sum of area ) (x g y
bot
=
Elements dA of vertical strips of height )] ( ) ( [ x g x f dx
and width dx from a x = to b x = , i.e.
= dA A
where (
) for sum.
Example: Find the area bounded by the graph of x y = 3 and 9
2
= x y .
Solution:
[ ] [ ]
= = =
b
a
bot top
b
a
dx y y dx x g x f A ) ( ) (
b a & are the intersection points.
x y = 3 , 9
2
= x y , then
9 3
2
= x x 0 12
2
= + x x , then
0 ) 3 )( 4 ( = + x x 4 = x , 3 = x
[ ] [ ]dx x x dx x x A
+ = =
3
4
2
3
4
2
) 12 ( ) 9 ( ) 3 (
6
343
)] 4 )( 12 (
2
) 4 (
3
) 4 (
[ )] 3 )( 12 (
2
3
3
3
[ ) 12
2 3
(
2 3 2 3
3
4
2 3
= +
+ =
(
x
x x
2
1
A
2
A
L
x
R
x
dy
dA
L
x
R
x
Example: Find the area bounded by the parabolas
2
x y =
2
2 x y = for 2 0 x .
Solution:
The Intersection points y
2
x y = ,
2
2 x y = , then
2 2
2 x x = 2 2
2
= x 1
2
= x 1 = x
Then
2 1
A A A + =
[ ] [ ]
= + =
2
1
2 2
1
0
2 2
4 ) 2 ( ) 2 ( dx x x dx x x A
Determine the area by integrating with respect to y :
Some region are best treated by regarding x as a function of y .
If the region is bounded by the two continuous curves ) ( y f x = , ) ( y g x = and the two lines c y = ,
d y = and ) ( ) ( y g y f for all y in the interval ] , [ d c , then the area is given by
= = =
d
c
L R
d
c
dy x x dy y g y f dA A ] [ )] ( ) ( [
where
= dA The area element dy x x
L R
] [ =
3
dA
dy
Example: Find the area bounded by the parabola
2
x y = , the line x y = 2 and 0 = y .
Solution:
Intersection points
2
x y = , x y = 2 , then
x x = 2
2
0 2
2
= + x x , then
0 ) 1 )( 2 ( = + x x 2 = x , 1 = x
Then
6
5
3
2
2
2 ] ) 2 [(
1
0
2 / 3
2 1
0
=
(
= = =
y
y
y dy y y dA A
If we need to integrate with respect to x , then the area will be given by
2 1
A A A + =
[ ] [ ]
+ =
2
1
1
0
2
0 ) 2 ( 0 dx x dx x A
6
5
2
2
3
2
1
2
1
0
3
=
|
|
\
|
+
|
|
\
|
=
x
x
x
4
5-2 Volume: Slicing Disks and Washers
Volume by Slicing (method of cross sections)
Assume a solid S of variable cross section ) (x A (the area varies with x ) from a x = to b x = .
) (x A ) (a A ) (x A ) (b A ) (x A
x
dx ] ) ( [ dx x A dV = dx
We slice the solid perpendicular to x axis. Each slice will be approximated by a cylinder of cross
section ) (x A and height dx . The volume of the slice element dV is
= = dx x A dV ) ( The volume element
The total volume can be obtained by summing the volume of all slices (
for sum), i.e.
] y
= =
b
a
dx x A dV V ) ( ) (d A
d
If the cross section ) ( y A varies with y axis from
c y = to d y = , then the volume element dV becomes
) ( [ y A
= = dy y A dV ) ( The volume element
and the total volume will be dy [
] ) ( [ dy y A dV =
= =
d
c
dy y A dV V ) ( c ) (c A
5
Example: Find the Volume of a pyramid whose base is a square with side ft h 600 = and a height is
ft w 320 = .
Solution:
The cross section area is variable of y , then the volume element becomes
dy y A dV ) ( =
where ) ( y A is a square of length x 2 at any distance y .
ft h 320 =
2 / w
x
h
y h
=
, then ) ( y A
dy x
y
y
h
y h w
x
16
15
300 )
320
320
)(
2
600
( ) )(
2
( =
= , then
y
2 2
)
16
15
300 ( 4 4 ) 2 )( 2 ( ) ( y x x x y A = = =
Then the total volume
ft w 600 =
= = =
= =
=
320
0
2
320
0
)
16
15
300 ( 4 ) ( dy y dy y A dV V
h y
y
3
320
0
3
000 , 400 , 38 )
16
15
300 ( )
3
1
)(
15
16
)( 4 ( ft y = =
6
) (x A
) (x f r =
dx
The Method of Disks (Volume of Solid of Revolution):
Solids of revolution are solids whose shapes can be generated by revolving plane region about
axis.
Assume a region bounded by the curve 0 ) ( = x f y and x axis for b x a and revolve it
about x axis. We can find the volume of this solid by slicing it perpendicular to x axis with
cross section is a circular disk of radius ) (x f y r = = .
) (x f y r = =
dx
Revolve about x axis
dx r dx x A dV
2
) ( = =
Solid of revolution
Then, the volume of slice circular disk is
dx y dx r dx x A dV
2 2
) ( = = =
The total volume of solid of revolution can be obtained by summing the volume of all slices
(
for sum), i.e.
dx x f dx r dV V
b
a
b
a
= = =
2 2
)] ( [
7
) ( y A
In a similar way, let the region is bounded by the curve 0 ) ( = y g x and y axis, for
d y c and revolve it about y axis, then
) (x g r =
r
dy dy
Revolve about the y axis Solid of revolution
Then, the volume of slice circular disk is
dy x dy r dy y A dV
2 2
) ( = = =
The total volume of solid of revolution can be obtained by summing the volume of all slices
(
for sum), i.e.
dy y g dy r dV V
d
c
d
c
= = =
2 2
)] ( [
8
dx
r
dx
dy dy
Example: Revolve the region under the curve x y = on the interval ] 4 , 0 [ about x axis and find the
volume of the resulting solid of revolution.
Solution:
= = = = =
4
0
4
0
2
4
0
2
8 ) ( dx x dx x dx r dV V
Example: Find the volume of the solid resulting from revolving the region bounded by the curve
2
4 x y = and 1 = y , 0 = x , 3 = x about y -axis.
Solution: If 0 = x , then 4 = y
y y
4
r
y x r = = 4
1
x
= = = = =
4
1
4
1
2
4
1
2
2
9
) 4 ( ) 4 (
dy y dy y dy r dV V
9
) (x f r
in
=
) (x f r
out
=
) (x g r
in
=
) (x f
) (x g
) (x f r
out
=
dx
r
dy
The Method of Washers:
If the region we revolve to generate a solid does not border on or cross the axis of rotation, the
solid has a hole in it. The cross sections perpendicular to the axis of revolution are washers instead
of disks.
If the rotation about x axis, so ) (x f r
out
= , ) (x g r
in
= , and
dx r r dV
in out
) (
2 2
= , then
= =
b
a
in out
dx r r dV V ) (
2 2
Example: Let R be the region bounded by
2
4 x y = and 0 = y . Find the volume of the solids
obtained by revolving R about each of the following: (a) the y axis, (b) the line 3 = y , (c)
the line 7 = y , (d) the line 3 = x .
Solution:
(a) The radius of the disk is y x r = = 4 , then
= = =
4
0
4
0
2 2
dy x dy r dV V
8 ) 4 ( ) 4 (
4
0
4
0
2
= = =
dy y dy y
10
dx
3
2
4 x y =
2
4 x y =
dx
y
(b) 3 =
I
r ,
2 2
7 3 ) 4 ( x x r
O
= + =
= = =
2
2
2
2
2 2 2 2 2
] 3 ) 7 ([( ) ( dx x dx r r dV V
I O
15
1472
=
(c) 7 =
O
r ,
2 2
3 ) 4 ( 7 x x r
I
+ = =
+ = = =
2
2
2
2
2 2 2 2 2
] ) 3 ( ) 7 [( ) ( dx x dx r r dV V
I O
5
576
=
11
y x = 4 y x + = 4
x r
O
=
3
x r
I
=
dx
3 / 1
y r
O
=
dy
2
y r
I
=
dy
(d) y r
O
+ = 4 3 , y r
I
= 4 3
= = =
4
0
2 2
) ( dy r r dV V
I O
= + =
4
0
2 2
64 ] ) 4 3 ( ) 4 3 [( dy y y
Example: Find the volume of the solid formed by revolving the plane region bounded by the two curves
2
y x = ,
3
x y = around: (a) the x axis, (b) the y axis, (c) the line 1 = x , (d) the
line 2 = y .
Solution:
(a) x r
O
= ,
3
x r
I
=
= =
1
0
2 2
) ( dx r r dV V
I O
14
5
] ) ( ) [(
1
0
2 3 2
=
dx x x
(b)
3 / 1
y r
O
= ,
2
y r
I
=
= =
1
0
2 2
) ( dy r r dV V
I O
5
2
] ) ( ) [(
1
0
2 2 2 3 / 1
= =
dy y y
12
1 = x
1
3 / 1
+ = y r
O
dy
1
2
+ = y r
I
2 = y
3
2 x r
O
= x r
I
= 2
(c) 1
3 / 1
+ = y r
O
, 1
2
+ = y r
I
= =
1
0
2 2
) ( dy r r dV V
I O
30
37
] ) 1 ( ) 1 [(
1
0
2 2 2 3 / 1
= + + =
dy y y
(d)
3
2 x r
O
= , x r
I
= 2
= =
1
0
2 2
) ( dx r r dV V
I O
21
4
] ) 2 ( ) 2 [(
1
0
2 2 3
= =
dx x x
13
1
r
2
r
t
r
x r =
= h
= t
h =
r =
= t
5.3 Volume by Cylindrical Shells:
Let a cylindrical shell of inner radius
1
r and outer radius
2
r and height h. The volume of the cylinder
is given by
h r r r r h r r V ) )( ( ) (
1 2 1 2
2
1
2
2
+ = =
let = = t r r ) (
1 2
The thickness shell
= =
+
r
r r
2
) (
1 2
The average radius
Then
) )( )( 2 ( ) 2 )( ( t h r h r t V = =
) 2 ( = x (the average radius) x (height) x (thickness)
=(Perimeter) x (height) x (thickness)
So, suppose that the plane region R bounded by ) (x f y = , x axis, a x = , b x = rotated about
y axis.
Cylindrical Shell of infinitesimal Thickness
The volume of a thin cylindrical shell dV of radius x r = , height ) (x f h = , and thickness dx t = is
given by
) ( ) ( ) 2 ( dx x f x dV =
=(Perimeter) x (height) x (thickness)
Then the total volume is the sum of such volumes (
for sum), i.e.
= =
b
a
dx x f x dV V ) ( ) 2 (
14
Revolving between two curves:
The region revolved about y axis.
If the plane region bounded by ) (x f y = , ) (x g y = ,
) ( ) ( x g x f , a x = , b x = revolved about y axis,
then
) )]( ( ) ( )[ 2 ( ) )( )( 2 ( dx x g x f x dx h r dV = =
=(Perimeter) x (height) x (thickness)
and the total volume becomes
= = =
b
a
b
a
dx x g x f x dx h r dV V )] ( ) ( [ ) 2 ( ) )( 2 (
The region revolved about x axis.
If the plane region bounded by ) ( y f x = , ) ( y g x = ,
) ( ) ( y g y f , c y = , d y = revolved about x axis,
then
) )]( ( ) ( )[ 2 ( ) )( )( 2 ( dy y g y f y dy h r dV = =
=(Perimeter) x (height) x (thickness)
and the total volume becomes
= = =
d
c
d
c
dy y g y f y dy h r dV V )] ( ) ( [ ) 2 ( ) )( 2 (
15
dx
y y h = ) 2 (
Example: Using the cylindrical shell method to find the volume of the solid formed by revolving the
region bounded by the graph of
2
4 x y = and the x axis about 3 = x .
Solution:
= =
2
2
) ( ) 2 ( dx h r dV V
64 ) 4 ( ) 3 ( 2
2
2
2
= =
dx x x
Example: Let R be a region bounded by the graphs x y = , x y = 2 , and 0 = y . Compute the volume
of the solid by revolving R about the lines: (a) 2 = y , (b) 1 = y , (c) 3 = x .
Solution:
Using cylindrical method
(a) Revolve about 2 = y
= =
1
0
) ( ) 2 ( dy h r dV V
3
10
] ) 2 [( ) 2 ( 2
1
0
= =
dy y y y
16
y y h = ) 2 (
1 + = y r
dx dx
1
r
2
r
2
h
1
h
dy
(b) Revolve about 1 = y
= =
1
0
) ( ) 2 ( dy h r dV V
3
8
] ) 2 [( ) 1 ( 2
1
0
= + =
dy y y y
(c) Revolve about 3 = x 3 = x
To use cylindrical shell, we would need to break
the region Rinto two pieces, since the height of
the cylindrical shells would be different for
] 1 , 0 [ x than for ] 2 , 1 [ x .
+ =
1
0
2 2
2
1
1 1
) ( ) 2 ( ) ( ) 2 ( dx h r dx h r V
4 ) ( ) 3 ( 2 ) 2 ( ) 3 ( 2
1
0
2
1
= + =
dx x x dx x x
Using the method of washers
= =
1
0
2 2
) ( dy r r dV V
I O
4 ] )) 2 ( 3 ( ) 3 [(
1
0
2 2
= =
dy y y
17
x
dx
h
Example: Using the cylindrical shells method to find the volume of the solid obtained by rotating the
region between x y = ,
2
x y = about the y axis.
Solution:
= =
1
0
) ( ) 2 ( dx h r dV V
6
] [ 2
1
0
2
= =
dx x x x
Example: Use the method of cylindrical shells to find the volume of the solid obtained by revolving the
region bounded by the curves x y =
2
,
3
x y = about 1 = x
Solution:
= =
1
0
) ( ) 2 ( dx h r dV V
30
37
] [ ) 1 ( 2
1
0
3
= + =
dx x x x
18
s
x
y
i
s
5-4 Arc Length and Surface Area
Arc Length:
By calculating the differential length element ds for the smooth curve ) (x f y = from a x = to b x = ,
then the total length will be given by
= ds s .
We first approximate the curve with several line segments ) ( s joining together as shown in the figure.
2 2 2
) ( ) ( ) ( y x s + =
2
2
2
2
) (
) (
1
) (
) (
x
y
x
s
+ =
2
2
) (
) (
1
) (
) (
x
y
x
s
+ =
By taking the limit 0 x we will have
2
2
0 0
) (
) (
1 lim
) (
) (
lim
x
y
x
s
x x
+ =
,
2
) ( 1
dx
dy
dx
ds
+ = ,
Then differential of length element dx
dx
ds
ds = is given by
dx
dx
dy
ds
(
+ =
2
) ( 1 , then dx
dx
dy
ds s
b
a
(
+ = =
2
) ( 1
Similarly,
2
) ( 1
dy
dx
dy
ds
+ = , dy
dy
dx
dy
dy
ds
ds
(
+ = =
2
) ( 1 , then
dy
dy
dx
ds s
b f
a f
(
+ = =
2
) (
) (
) ( 1
19
ds
ds
dx
y
Example: Find the arc length of the curve
2 / 3
x y = on ] 5 , 0 [ .
Solution:
2 / 3
x y = Q , then
2 / 1
2
3
x
dx
dy
= , then
5
0
2 / 3
5
0
5
0
2
2 / 1
4
9
1 )
3
2
( )
9
4
(
4
9
1
2
3
1
|
\
|
+ = + =
|
\
|
+ =
x dx x dx x s
27
335
1 ) 5 (
4
9
1
27
8
2 / 3
=
(
(
\
|
+ =
Example: Find the arc length of the curve
y
y x
2
1
6
1
3
+ = for 2 1 y .
Solution:
y
y x
2
1
6
1
3
+ = Q , then
2
2
2
1
2
1
y
y
dy
dx
= , then
dy
y
y dy
y
y s
+ + =
|
|
\
|
+ + =
2
1
4
4
2
1
2
2
2
4
1
4
1
2
1
2
1
2
1
1 1
12
17
2
1
2
1
2
1
2
1
2
1
2
1
2
2
2
2
2
=
|
|
\
|
+ =
|
|
\
|
+ =
dy
y
y dy
y
y
Surface Area:
The surface area of revolution that generated by revolving an arc around an axis can be obtained by
calculating the sum of the surface element area dA due to revolve the arc element length ds around the
axis, i.e.
= dA S
Let the arc graph ) (x f y = revolved about x axis from a x = to b x = to generate the surface of
revolution S shown in the figure.
Portion of a right circular cone
20
We decompose the surface S into small sections whose areas dA can be approximated by the surface
areas of frustum of a cone (portion of a right circular cone).
Since the surface area of the right cone with base radius r and
slant height L is given by
L r A =
Then the surface area of the frustum cone with slant height l
and upper and lower radii
1
r and
2
r can be obtained by
subtracting the two areas of the right cones shown in the figure.
i.e.
1 1 1 2 1 2
) ( l r l l r A A A + = =
l r l r r
2 1 1 2
) ( + =
Since
l l
l
r
r
+
=
1
1
2
1
, l r r l r ) (
1 2 1
= , then
l r r A ) (
2 1
+ = , ) 2 ( 2 = = l r A x (average radius) x (slant height)
where
2
2 1
r r
r
+
= is the average radius. If l is the differential ds then
1
r and
2
r would be y r = . Then
the surface area element dA will be given by
ds y dA 2 =
Then the total surface area will be given by
(
+ = = =
b
a
dx
dx
dy
x f ds y dA S
2
1 ) ( 2 2 , about x axis
Or,
(
+ =
) (
) (
2
1 2
b f
a f
dy
dy
dx
y , about x axis
If the curve revolved about y axis then the surface area becomes
= = ds x dA S 2 , about y axis
21
y
3
x y =
ds
)
`
y
x
0 2
y
2
x y =
ds
4 4 4 3 4 4 4 2 1
x
x
Example: Find the surface area of the surface that generated by revolving the curve
3
x y = for
2 0 x about x axis.
Solution:
ds y dA 2 = , dx x dx
dx
dy
ds
2 2
2
) 3 ( 1 1 + =
|
\
|
+ =
Then
dx x x dx
dx
dy
y S
+ =
|
\
|
+ =
2
0
2
0
4 3
2
9 1 ) ( 2 1 2
( ) 04 . 203 ) 2 ( 9 1
108
4 2 / 3
4
= + =
Example: Find the surface area of the surface that generated by revolving the curve
2
x y = about y
axis for 2 0 x .
Solution:
= + =
|
\
|
+ =
2
0
2
2
0
2
3
13
) 2 ( 1 2 1 2 dx x x dx
dx
dy
x S
You might also like
- Unit5 HPPDocument29 pagesUnit5 HPPRanjan NayakNo ratings yet
- Biology CellsDocument12 pagesBiology CellsGift ag bruhNo ratings yet
- Pure M Ath - Geom Etric Applications of Definite Integrals: Area of Plane FiguresDocument4 pagesPure M Ath - Geom Etric Applications of Definite Integrals: Area of Plane FiguresFrancis WongNo ratings yet
- Group 11: Areas and VolumesDocument32 pagesGroup 11: Areas and VolumesLuxemberg NgNo ratings yet
- Name:: Math 142.009 Exam 3 SolutionsDocument5 pagesName:: Math 142.009 Exam 3 SolutionsАрхи́пNo ratings yet
- Notes Shell MethodDocument5 pagesNotes Shell MethodvikasNo ratings yet
- Lecture 2 Calculus of Multi Variables 2011Document22 pagesLecture 2 Calculus of Multi Variables 2011Yiauw ShenqNo ratings yet
- Volumes by Cylindr Ical ShellsDocument7 pagesVolumes by Cylindr Ical ShellssantiagoNo ratings yet
- Volumes by Cylindrical ShellsDocument7 pagesVolumes by Cylindrical ShellsAneesh Amitesh ChandNo ratings yet
- Updated - Tutorial On Unit IIDocument4 pagesUpdated - Tutorial On Unit IItejas chikhlikarNo ratings yet
- Areas (Part 1)Document7 pagesAreas (Part 1)Sachin KumarNo ratings yet
- Lecture in CalculusDocument36 pagesLecture in CalculusJovelynBrozasBihisNo ratings yet
- Volumes by Cylindrical ShellsDocument7 pagesVolumes by Cylindrical Shellseomer1968No ratings yet
- Integration PDFDocument8 pagesIntegration PDFAre Peace El MananaNo ratings yet
- Applications of IntegrationDocument75 pagesApplications of IntegrationweglisotterNo ratings yet
- Calculus Cheat Sheet Integrals ReducedDocument3 pagesCalculus Cheat Sheet Integrals ReducedShahnaz GazalNo ratings yet
- Chap 3 ApplicationsDocument14 pagesChap 3 ApplicationsGrace HeNo ratings yet
- CHAPTER 2 - Integration Part 4 DNDDocument30 pagesCHAPTER 2 - Integration Part 4 DNDmuhdkamal11No ratings yet
- 2.2 Volumes by Washers&Disks - NotesDocument8 pages2.2 Volumes by Washers&Disks - NotesKelseyNo ratings yet
- AOD1Document8 pagesAOD1nalini7723No ratings yet
- Lecture 21 - MTH101 IIT KanpurDocument3 pagesLecture 21 - MTH101 IIT KanpurAsish MahapatraNo ratings yet
- Integrals DoubledDocument16 pagesIntegrals DoubledsabbysamuraNo ratings yet
- Lecture 8Document7 pagesLecture 8Vikas PandeyNo ratings yet
- MATH 2300 - Review Problems For Exam 2: Corrected AnswersDocument8 pagesMATH 2300 - Review Problems For Exam 2: Corrected Answersammar_harbNo ratings yet
- 02-Applications of The IntegralsDocument32 pages02-Applications of The IntegralsGeeta MNo ratings yet
- 15.1 Double Integrals Over RectanglesDocument16 pages15.1 Double Integrals Over RectanglesHebatallah Mujahed Mohmoud KanaNo ratings yet
- H2 Mathematics Cheat Sheet by Sean LimDocument27 pagesH2 Mathematics Cheat Sheet by Sean LimGale HawthorneNo ratings yet
- Areas of Bounded Regions: B Fxdxor Ydx A D Fydyor Xdy CDocument1 pageAreas of Bounded Regions: B Fxdxor Ydx A D Fydyor Xdy CRaja KushwahNo ratings yet
- Schaumcalculus p2Document131 pagesSchaumcalculus p2plokplokplokNo ratings yet
- Calculus I: Unit 10: Applications of Definite IntegralsDocument63 pagesCalculus I: Unit 10: Applications of Definite IntegralsTÂN NGUYỄN DUYNo ratings yet
- K03052 - 20200424155900 - 6.2 Applications of Integration - Volumes of RevolutionDocument22 pagesK03052 - 20200424155900 - 6.2 Applications of Integration - Volumes of Revolutionhariz syazwan100% (1)
- Calculus Cheat Sheet Integrals ReducedDocument3 pagesCalculus Cheat Sheet Integrals ReducedFadzilah YayaNo ratings yet
- 1 Double Integrals in Cartesian CoordinatesDocument4 pages1 Double Integrals in Cartesian Coordinatesjurilyn alvadorNo ratings yet
- 7.3 V W K C S: Olumes ITH Nown Ross EctionsDocument10 pages7.3 V W K C S: Olumes ITH Nown Ross EctionsdonaldbistriNo ratings yet
- Cbse - Areas Differential EquationsDocument11 pagesCbse - Areas Differential EquationsSankar AnanthyaNo ratings yet
- Lecture 11 - Area Between CurvesDocument26 pagesLecture 11 - Area Between CurvesbananaNo ratings yet
- Functions of Several Variables2Document5 pagesFunctions of Several Variables2ngothaiquynhNo ratings yet
- Advanced Technology M7 "Fields and Waves" Vector Field TheoryDocument8 pagesAdvanced Technology M7 "Fields and Waves" Vector Field TheorysFDfdsNo ratings yet
- Calculus Reference (SparkCharts)Document2 pagesCalculus Reference (SparkCharts)www_webb100% (1)
- Chapter 5 Applications of Definite IntegDocument12 pagesChapter 5 Applications of Definite IntegAbdul MajidNo ratings yet
- Sec-1.1 SolDocument11 pagesSec-1.1 SolaltwirqiNo ratings yet
- CC Calculus Chapter 6 AnswersDocument23 pagesCC Calculus Chapter 6 AnswersAganon AristotleNo ratings yet
- Double IntegralsDocument13 pagesDouble IntegralsArvind MeenaNo ratings yet
- Martin, Vector, WhaleDocument10 pagesMartin, Vector, WhaleMartin Moltke WozniakNo ratings yet
- 6 Applications of The Definite IntegralDocument4 pages6 Applications of The Definite IntegralBruce ChiarelliNo ratings yet
- Pertemuan 2Document17 pagesPertemuan 2Syarifah Humaira Al'mudhirNo ratings yet
- Calculus Ich 13Document29 pagesCalculus Ich 13nqnghia22No ratings yet
- Triple SubstitutionDocument4 pagesTriple SubstitutionTinaNo ratings yet
- Mth301 Mid Fall 2010Document8 pagesMth301 Mid Fall 2010Prince IslamabadNo ratings yet
- Guc - Math203: Lecture # 5Document17 pagesGuc - Math203: Lecture # 5Amr Ashraf KhalilNo ratings yet
- Handout IIDocument5 pagesHandout IIMarian Galvez-LuisNo ratings yet
- Calculus Cheat Sheet IntegralsDocument5 pagesCalculus Cheat Sheet Integralsapi-322359712No ratings yet
- Calculus Cheat Sheet IntegralsDocument5 pagesCalculus Cheat Sheet Integralstasos_rex31390% (1)
- Centroids and Centre of GravityDocument11 pagesCentroids and Centre of GravityJoshua ReynoldsNo ratings yet
- Area and Differterterterterential EquationsDocument8 pagesArea and Differterterterterential EquationsPrithviraj NetkeNo ratings yet
- Transformation of Axes (Geometry) Mathematics Question BankFrom EverandTransformation of Axes (Geometry) Mathematics Question BankRating: 3 out of 5 stars3/5 (1)
- Free Printable Calendar 20163Document12 pagesFree Printable Calendar 2016333ndgrNo ratings yet
- Maurice Nicoll The Mark PDFDocument4 pagesMaurice Nicoll The Mark PDFErwin KroonNo ratings yet
- Daily To Do Lists PDFDocument1 pageDaily To Do Lists PDFAfiqah ZainuddinNo ratings yet
- Maurice Nicoll The Mark PDFDocument4 pagesMaurice Nicoll The Mark PDFErwin KroonNo ratings yet
- $Xwrqrprxv1Dyljdwlrqri0Reloh5Rerw8Vlqj - Lqhfw6Hqvru: 5th International Conference On Computer & Communication EngineeringDocument4 pages$Xwrqrprxv1Dyljdwlrqri0Reloh5Rerw8Vlqj - Lqhfw6Hqvru: 5th International Conference On Computer & Communication EngineeringAfiqah ZainuddinNo ratings yet
- 2 Features Selection For Multi-Camera TrackingDocument4 pages2 Features Selection For Multi-Camera TrackingAfiqah ZainuddinNo ratings yet
- Basic Concepts of Electricity - Electronics TextbookDocument2 pagesBasic Concepts of Electricity - Electronics TextbookAfiqah ZainuddinNo ratings yet
- Sains Tingkatan 1 (Bab 1)Document4 pagesSains Tingkatan 1 (Bab 1)JeyShidaNo ratings yet
- Writing An Academic Journal Article PDFDocument87 pagesWriting An Academic Journal Article PDFKarenJohanaGarayNo ratings yet
- Form 3 Chapter 9Document3 pagesForm 3 Chapter 9naza9775100% (5)
- CVPR2013Document8 pagesCVPR2013Afiqah ZainuddinNo ratings yet
- Lec 1 Introduction To Power ElectronicsDocument38 pagesLec 1 Introduction To Power ElectronicsAfiqah Zainuddin100% (1)
- Form 3 Chapter 10Document4 pagesForm 3 Chapter 10naza977575% (4)
- Basic Concepts of Electricity - Electronics TextbookDocument2 pagesBasic Concepts of Electricity - Electronics TextbookAfiqah ZainuddinNo ratings yet
- Chapter 6 (Integration Techniques) : DX X XDocument27 pagesChapter 6 (Integration Techniques) : DX X XAfiqah ZainuddinNo ratings yet
- Form 3 Chapter 1Document6 pagesForm 3 Chapter 1naza977590% (29)
- Chap 2Document48 pagesChap 2Afiqah ZainuddinNo ratings yet
- Derivatives & Integrals FormulasDocument8 pagesDerivatives & Integrals Formulasdragon55knightNo ratings yet
- Lecture #19: Moments of InertiaDocument19 pagesLecture #19: Moments of InertiaAfiqah ZainuddinNo ratings yet
- Lecture #19: Moments of InertiaDocument19 pagesLecture #19: Moments of InertiaAfiqah ZainuddinNo ratings yet