Solution

Week 71

(1/19/04)

Maximum trajectory length

Let be the angle at which the ball is thrown. Then the coordinates are given by
x = (v cos )t and y = (v sin )t gt2 /2. The ball reaches its maximum height at
t = v sin /g, so the length of the trajectory is
L = 2
= 2

Z v sin /g

Z v sin /g q
0

= 2v cos

dx
dt

dx
dt

dt

(v cos )2 + (v sin gt)2 dt

Z v sin /g

gt
1 + tan
v cos

dt.

(1)

Letting z tan gt/v cos , we obtain

L=

2v 2 cos2
g

Z 0

1 + z 2 dz.

tan

(2)

Letting z tan , and switching the order of integration, gives

L=

2v 2 cos2
g

Z
0

d
.
cos3

(3)

You can either look up this integral, or you can derive it (see the remark at the end
of the solution). The result is

L =
=

2v 2 cos2 1 sin
1 + sin

+ ln
2
g
2 cos
cos

2
v
sin + 1
sin + cos2 ln
.
g
cos

(4)

As a double-check, you can verify that L = 0 when = 0, and L = v 2 /g when

= 90 . Taking the derivative of eq. (4) to find the maximum, we obtain

0 = cos 2 cos sin ln

1 + sin
cos

+ cos2

cos
1 + sin

This reduces to
1 = sin ln

1 + sin
.
cos

cos2 + (1 + sin ) sin

.
cos2
(5)
(6)

Finally, you can show numerically that the solution for is 0 56.5 .
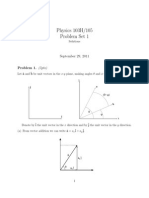
A few possible trajectories are shown below. Since it is well known that = 45
provides the maximum horizontal distance, it follows from the figure that the 0
yielding the arc of maximum length must satisfy 0 45 . The exact angle, however,
requires the above detailed calculation.
1

= 45
path

Remark: Lets now show that the integral in eq. (3) is given by

Z
d
1 sin
1 + sin
=
+ ln
.
cos3
2 cos2
cos

(7)

Letting c cos and s sin for convenience, and dropping the d in the integrals, we
have
Z
Z
1
c
=
c3
c4
Z
c
=
(1 s2 )2
2
Z
1
1
1
=
c
+
4
1+s 1s

Z
Z
1
c
c
1
c
=
+
+
4
(1 + s)2
(1 s)2
2
(1 s2 )

Z
1
1
1
1
c
c
=
+
+
+
4 1+s 1s
4
1+s 1s

s
1
=
+
ln(1
+
s)

ln(1

s)
2(1 s2 ) 4

s
1
1+s
=
+
ln
2c2
4
1s

1 s
1+s
=
+
ln
,
(8)
2 c2
c
as we wanted to show.