Professional Documents
Culture Documents
BTEC HNC - Science - Application of DC and AC Theory
Uploaded by
Brendan BurrCopyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
BTEC HNC - Science - Application of DC and AC Theory
Uploaded by
Brendan BurrCopyright:
Available Formats
Application of DC & AC Theory
Engineering Science By Brendan Burr
Brendan Burr BTEC Higher National Certificate in Electronics
Application of DC & AC Theory
Table of Contents
TABLE OF CONTENTS...........................................................2 TASK 1................................................................................5 1.1 Two storage batteries, A and B, are connected in parallel for charging from a DC source having an open circuit voltage of 14V and an internal resistance of 0.15 Ohms. The opencircuit voltage of A is 11V and that of B is 11.5V; the internal resistances are 0.06 Ohms and 0.05 Ohms respectively. Calculate the initial charging currents. ................................5 Solution:-.........................................................................................5 Check:-.............................................................................................7 1.2 In the diagram below find the current through the 8 Ohm resistor. ............................................................................8 Solution (Circuit 1):-.........................................................................8 Check (Circuit 1):-..........................................................................10 Solution (Circuit 2):-.......................................................................11 Check (Circuit 2):-..........................................................................13 Solution (Overall Circuit):-..............................................................14 Check (Overall Circuit):-.................................................................14 TASK 2..............................................................................15 2.1 Explain how complex waveforms are produced from sinusoidal waveforms........................................................15 Solution:-.......................................................................................15 2.2 Synthesise the following complex waveform graphically using a spreadsheet: .......................................................15 Solution:-.......................................................................................15 2.3 Plot a minimum of 100 points at intervals of (Periodic Time T)/100 Seconds.......................................................15 Solution:-.......................................................................................15 2.4 Produce a print out of the graph and data.....................15 Solution:-.......................................................................................15 2.5 Describe how electrical and electronic devices produce complex waveforms...........................................................16 Solution:-.......................................................................................16 2.6 Describe the effects of complex waveforms on electrical and electronic systems......................................................16 Solution:-.......................................................................................16
Brendan Burr BTEC Higher National Certificate in Electronics
Application of DC & AC Theory
TASK 3..............................................................................17 A circuit consists of three branches in parallel. Branch A is a 10 Ohm resistor, Branch B is a coil of resistance 4 Ohms and inductance of 0.02H, and Branch C is an 8 Ohm resistor in series with a 200uF capacitor. The combination is connected to a 100V, 50Hz supply. Find the various branch currents and then, by resolving into in-phase and quadrature components, determine the total current taken from the supply..............17 Solution:-.......................................................................................17 Check:-...........................................................................................20 A 31.8uF capacitor, a 127.5mH inductor of resistance 30 Ohms and a 100 Ohms resistor are all connected in parallel to a 200V, 50 Hz supply. Find the various branch currents and the, by resolving into in-phase and quadrature components, determine the total current taken from the supply..............22 Solution:-.......................................................................................22 Check:-...........................................................................................25 TASK 4..............................................................................27 4.1 A 1kOhm resistor is connected across the secondary windings of an ideal transformer whose secondary voltage is 100 Volts. The current in the primary windings is 10mA......27 (a) Draw a circuit diagram.................................................27 Solution:-.......................................................................................27 (b) Determine the secondary current..................................27 Solution:-.......................................................................................27 (c) Determine the primary voltage......................................28 Solution:-.......................................................................................28 (d) Determine the transformer turns ratio..........................28 Solution:-.......................................................................................28 Check (Overall Circuit):-.................................................................29 4.2 An ideal transformer has 1000 primary turns and 100 secondary turns. If the primary winding is connected to a 230V AC supply the secondary is connected to a 100 Ohms resistive load:...................................................................30 (a) Draw a circuit diagram.................................................30 Solution:.........................................................................................30 (b) Determine the secondary voltage..................................30 Solution:.........................................................................................30 (c) Determine the secondary current..................................31 Solution:.........................................................................................31 3
Brendan Burr BTEC Higher National Certificate in Electronics
Application of DC & AC Theory
(d) Determine the power supplied in the primary circuit......31 Solution:.........................................................................................31 Check:-...........................................................................................31 Check (Overall Circuit):-.................................................................32 APPENDIX 1......................................................................33 EVALUATION.....................................................................34 CONCLUSION.....................................................................35 Books...............................................................................36 Catalogues........................................................................36 Websites...........................................................................36
Brendan Burr BTEC Higher National Certificate in Electronics
Application of DC & AC Theory
Task 1
1.1 Two storage batteries, A and B, are connected in parallel for charging from a DC source having an open circuit voltage of 14V and an internal resistance of 0.15 Ohms. The open-circuit voltage of A is 11V and that of B is 11.5V; the internal resistances are 0.06 Ohms and 0.05 Ohms respectively. Calculate the initial charging currents.
Solution:-
IO C
= A + B u to I I E ai n q
_1
Loop A: EOC I OC ROC I A RA E A = 0 14 0.15 I OC 0.06 I A 11 = 0 3 0.15 I OC 0.06 I A = 0 0.15 I OC + 0.06 I A = 3 Multiply _ both _ sides _ by _
2.5 I O + A =0 u to I 5 E ai n q C
50 3
_ 2
Loop B: EB + I B RB I A RA E A = 0 11.5 + 0.05 I B 0.06 I A 11 = 0 0.5 + 0.05 I B 0.06 I A = 0 0.05 I B 0.06 I A = 0.5 Multiply _ both _ sides _ by _
5 25 IB I A = Equation 6 3
50 3
_3
Brendan Burr BTEC Higher National Certificate in Electronics
Application of DC & AC Theory
I A shows up in Equations 2 and 3, therefore substituting Equation 1 into Equations 2 and 3, as follows, gives: I A = I OC I B Equation _ 1 2.5 I OC + ( I OC I B ) = 50 Equation _ 4 5 25 I B ( I OC I B ) = Equation _ 5 6 3 Simplifying Equations 4 and 5 leaves:
3.5I OC I B = 50 Equation _ 4 I OC + 11 25 IB = Equation _ 5 6 3
Multiply Equation 4 by 77 11 275 I OC I B = 12 6 3 Then add Equation 5: 77 11 275 I OC I B = 12 6 3 + 11 25 I OC + I B = 6 3 = 65 250 I OC = 12 3 I OC =
IO C
11 : 6
200 13 Amps
= 5 .3 4 1 3 1 8658
Brendan Burr BTEC Higher National Certificate in Electronics
Application of DC & AC Theory
Substituting I OC into Equation 5, gives: 200 11 25 + IB = 13 6 3 11 200 25 IB = 6 13 3 11 275 IB = 6 39 275 11 IB = 39 6 IB = 50 13 Amps
I B = .8 6 5 8 6 3 413 4
Substituting I OC and I B into Equation 1, gives: IA = 200 50 13 13 150 13 Amps
IA =
I A =1 .5 8 6 5 1 3414
Check:-
Brendan Burr BTEC Higher National Certificate in Electronics
Application of DC & AC Theory
1.2
In the diagram below find the current through the 8 Ohm resistor.
Solution (Circuit 1):Redraw the circuit with one Voltage Source:
Alternative Circuit:
1 1 1 5 = + = R A R5 R4 24 R A = 4.8 1 1 1 149 = + = RB R2 R3 + R A 1110 RB = 7.44966443 RT = R1 + RB RT = 12.44966443 I1 = E1 4 = RT 12.44966443
A
I1 = .3 19 8 0 0 2 23 0 5
Brendan Burr BTEC Higher National Certificate in Electronics
Application of DC & AC Theory
Voltage drop across R1 is represented by: V1 = I1 R1 V1 = 0.3212938005 5
V1 = .6 6 6 0 3 1 0 4 90 V
Voltage drop across R2 is represented by: V2 = E1 V1 V2 = 4 1.606469003
V2 = .33 3 97 2 9 50 9 V
I2 =
V2 2.392530997 = R2 15
A
I 2 = .19 6 73 0 5 58 31
I 3 = I1 I 2 I 3 = 0.3212938005 0.1595687331
I 3 = .1 1 2 0 7 0 67564 A
Voltage drop across R3 is represented by: V3 = I 3 R3 V3 = 0.1617250674 10
V 3 = .6 7 5 6 4 1 1207 V
Voltage drop across R4 is represented by: V4 = V2 V3 V4 = 2.393530997 1.617250674
V 4 = .7 6 8 3 3 0 72 0 2 V
Brendan Burr BTEC Higher National Certificate in Electronics
Application of DC & AC Theory
I5 =
V4 0.776280323 = R5 12
2A
I 5 = .0 4 9 0 6 0 66029
I4 =
V4 0.776280323 = R4 8
8A
I 4 = . 07 3 0 0 0 90 5 43
Check (Circuit 1):Therefore, I1 = I 2 + I 4 + I 5 :
I1 = 0.1595687331 + 0.0970350403 8 + 0.0646900269 2 I1 = 0.3212938005 A
10
Brendan Burr BTEC Higher National Certificate in Electronics
Application of DC & AC Theory
Solution (Circuit 2):Redraw with second Voltage Source:
Alternative Circuit:
1 1 1 4 = + = R A R1 R2 15 R A = 3.75 1 1 1 87 = + = RB R4 R3 + R A 440 RB = 5.057471264 RT = R5 + RB RT = 17.05747126 I5 = E2 6 = RT 17.05747126
A
I 5 = .3 1 5 0 1 0 57226
11
Brendan Burr BTEC Higher National Certificate in Electronics
Application of DC & AC Theory
Voltage drop across R5 is represented by: V1 = I 5 R5 V1 = 0.3517520216 12
V1 = .21 2 2 9 4 2 04 5 V
Voltage drop across R4 is represented by: V4 = E2 V1 V4 = 6 4.221024259
V4 = .78 7 7 1 1 7954 V
I4 =
V4 1.778975741 = R4 8
A
I 4 = .2 2 7 9 7 0 2316 6
I3 = I5 I4 I 3 = 0.3517520216 0.2223719676
I 3 = .1 9 8 0 4 0 2305 A
Voltage drop across R3 is represented by: V3 = I 3 R3 V3 = 0.129380054 10
V3 = .2 3 0 5 1 9804 V
Voltage drop across R2 is represented by: V2 = V4 V3 V2 = 1.778975741 1.29380054
V2 = .4 57 2 1 0 8150 V
12
Brendan Burr BTEC Higher National Certificate in Electronics
Application of DC & AC Theory
I1 =
V2 0.485175201 = R1 5
A
I1 = .0 7 30 0 0 9 05 4 2
I2 =
V2 0.485175201 = R1 15
A
I 2 = .0 2 4 0 3 0 3351 4
Check (Circuit 2):Therefore, I 5 = I1 + I 2 + I 4 :
I 5 = 0.0970350402 + 0.0323450134 + 0.2223719676 I 5 = 0.3517520216 A
13
Brendan Burr BTEC Higher National Certificate in Electronics
Application of DC & AC Theory
Solution (Overall Circuit):By merging the two circuits together we get: I1 = I1( Circuit1) I1(Circuit 2) I1 = 0.3212938005 0.0970350402
I 1 = .2 45 70 0 2 28 6 3 A
I 2 = I 2 ( Circuit1) + I 2 ( Circuit 2 ) I 2 = 0.1595687331 + 0.0323450134
I 2 = .1 11 7 6 0 99 34 5 A
I 3 = I 3( Circuit1) I 3( Circuit 2) I 3 = 0.1617250674 0.129380054
I 3 = .0 2 4 0 3 0 33514 A
I 4 = I 4 ( Circuit1) + I 4 (Circuit 2 ) I 4 = 0.0970350403 8 + 0.2223719676
I 4 = .3 9 0 0 8 0 1 470 A
I 5 = I 5( Circuit1) I 5( Circuit 2 ) I 5 = 0.0646900269 2 0.3517520216
I 5 = 0.2 7 6 9 4 80197 A
Check (Overall Circuit):-
14
Brendan Burr BTEC Higher National Certificate in Electronics
Application of DC & AC Theory
Task 2
2.1 Explain how complex waveforms are produced from sinusoidal waveforms.
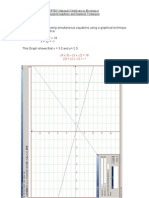
Solution:Complex waveforms are comprised of a fundamental component together with a number of harmonic components, each of which have a specific amplitude and phase relative to the fundamental. When a fundamental signal receives a harmonic they are added together. This deforms the shape of the overall waveform which is directly related to the sum of the two waveforms. 2.2 Synthesise the following complex waveform graphically using a spreadsheet: v = 200 sin t + 30 sin t .
Solution:See Appendix 1 2.3 Plot a minimum of 100 points at intervals of (Periodic Time T)/100 Seconds.
Solution:See Appendix 1 2.4 Produce a print out of the graph and data.
Solution:See Appendix 1
15
Brendan Burr BTEC Higher National Certificate in Electronics
Application of DC & AC Theory
2.5
Describe how electrical and electronic devices produce complex waveforms.
Solution:Electrical and electronic devices can produce complex waveforms (due to creating Harmonics), in many different ways. The main cause of harmonics being created is due to the mechanical properties of the device, for example tooth ripple in AC Generators, caused by the effect of the slots that accommodate the windings, or because of the non-sinusoidal air-gap flux distribution. For a rectifier to create a half cycle the waveform needs to be removed of its negative cycle, due to the low impedance in one direction and a high impedance in the opposite, diodes create complex waveforms. Harmonics are produced in devices that have a non-linear response to their inputs. Non-linear circuit element (i.e. those in which the current flowing through them is not proportional to the applied voltage) include rectifiers and any large-signal electronic amplifier in which diodes, transistors, valves or iron-cored inductors are used. 2.6 Describe the effects of complex waveforms on electrical and electronic systems.
Solution:If a complex waveform is fed into electrical and electronic devices then the device may fail to work correctly. This is because the amplitude of the waveform is altered, so may damage the device if too much voltage/current is fed into it. The input waveform will also have a possible phase shift which will mean that the device may not operate to the required time response and affect output. The output would also be irregular as the components will produce even more of a complex waveform, as explained above, and therefore the overall effect could be something that is extremely difficult to calculate/predict.
16
Brendan Burr BTEC Higher National Certificate in Electronics
Application of DC & AC Theory
Task 3
A circuit consists of three branches in parallel. Branch A is a 10 Ohm resistor, Branch B is a coil of resistance 4 Ohms and inductance of 0.02H, and Branch C is an 8 Ohm resistor in series with a 200uF capacitor. The combination is connected to a 100V, 50Hz supply. Find the various branch currents and then, by resolving into in-phase and quadrature components, determine the total current taken from the supply. Solution:-
BRANCH A =
ZA = 0 1
BRANCH B = Z B = 4 + j ( 2 50 0.02 )
Z B = +j 2 4
1 BRANCH C = Z C = 8 j 2 50 200 10 6
Z C = j1 .9 5 9 3 8 5 1 4 41
Current, I =
V Z
Impedance, Z, for the three branch parallel circuit: 1 1 1 1 = + + Z Z A Z B ZC 1 =Y Z
17
Brendan Burr BTEC Higher National Certificate in Electronics
Application of DC & AC Theory
Admittance, Y1 = 1 10
1 : ZA
Y1 =
Y1 = 0.1
Siemens (Rectangular) Siemens (Polar) 1 : ZB
OR
Y1 =0.1 O 0
Admittance, Y2 = 1 4 + j 2
Y2 =
Y2 =
1 4 j 2 4 + j 2 4 j 2 4 j 2 2 42 + ( 2 ) 4 j 2 55.4784176
9 0.1 3 5 5 7 j 1 2 48 6
Y2 =
Y2 =
Y2 = .0 2 0 1 9 0 7 10 07
Siemens (Rectangular)
OR
Y2 = .1 4 5 3 8 0 32 7 1 5 .5 8 6 4 7 1 3 3
O
Siemens (Polar)
18
Brendan Burr BTEC Higher National Certificate in Electronics
Application of DC & AC Theory
Admittance, Y3 =
1 : ZC
Y3 =
1 8 j15.91549431 1 8 + j15.91549431 8 j15.91549431 8 + j15.91549431 8 + j15.91549431 82 + 15.915494312 8 + j15.91549431 317.3029591
+ 0.00569 j 51866 3
Y3 =
Y3 =
Y3 =
Y3 = .05147 0 22293
Siemens (Rectangular)
OR
Y3 = .0 6 3 7 5 0 51879 .3 3 8 8 6 3 1 398
O
Siemens (Polar)
Current for BRANCH A, is given by: I A = V Y1 I A = 1000O 0.10O
I A = 0 +j 0 1
) (
Amps (Rectangular) Amps (Polar)
OR
IA = 0 O 1 0
Current BRANCH B, is given by: I B = V Y2 I B = 1000O 0.134257318 57.5183634 O
I B = .2 01 98 7 1 0 07 1 .35 5 7 j 1 24 8 6
) (
Amps (Rectangular)
OR
I B =3 .45 38 1 271 5 .5 8 6 4 7 1 3 3
O
Amps (Polar)
19
Brendan Burr BTEC Higher National Certificate in Electronics
Application of DC & AC Theory
Current BRANCH C, is given by: I C = V Y3 I C = 1000O 0.0561387758 63.31338988 O
I C = .5 1 47 6 2 2 29 2 + 5.0 5 6 9 4 j 1865
) (
Amps (Rectangular)
O
OR
I C = .6 3 7 5 5 1878 .3 3 8 8 6 3 1398
Amps (Polar)
Total Admittance, Y = Y1 + Y2 + Y3 : Y = ( 0.1) + ( 0.0721001097 9 j 0.1132545876 ) + ( 0.0252124973 + j 0.0501586696 3) Y = .17167 0 93201 0.03997 j 60519 7 Siemens (Rectangular) OR Y = .27540 0 01501 7 .7352 1 3009 Siemens (Polar)
O
Total Current is given by: Total Current, I = V = VY Z I = 1000O 0.2071554001 17.73305029 O
) (
I = .7167 1 9 3201
6.39976 j 0519
Amps (Rectangular)
O
OR
I = .7540 2 0 1501 7 .7352 1 3009
Amps (Polar)
Check:I = I A + I B + I C = (10 + j 0 ) + ( 7.210010978 j11 .32545876
+ ( 2.521249726 + j 5.015866954
)
O
I = 19 .73126072 j 6.309591806 20 .71554002 17 .73305031
On the following Graph: The Red Waveform represents Total Current ( I ) in Polar. The Blue Waveform represents BRANCH A ( I A ) in Polar. The Magenta Waveform represents BRANCH B ( I B ) in Polar. The Dark Green Waveform represents BRANCH C ( I C ) in Polar.
20
Brendan Burr BTEC Higher National Certificate in Electronics
Application of DC & AC Theory
21
Brendan Burr BTEC Higher National Certificate in Electronics
Application of DC & AC Theory
A 31.8uF capacitor, a 127.5mH inductor of resistance 30 Ohms and a 100 Ohms resistor are all connected in parallel to a 200V, 50 Hz supply. Find the various branch currents and the, by resolving into in-phase and quadrature components, determine the total current taken from the supply. Solution:-
1 BRANCH A = Z A = 0 j 2 50 31.8 10 6
= 10 .0745 0 j 0 948
BRANCH B = Z B = 30 + j 2 50 127.5 10 3
Z B =0 + 4 .0503 3 j 0 5363
))
BRANCH C= Current, I = V Z
ZC = 0 10
Impedance, Z, for the three branch parallel circuit: 1 1 1 1 = + + Z Z A Z B ZC 1 =Y Z
22
Brendan Burr BTEC Higher National Certificate in Electronics
Application of DC & AC Theory
Admittance, Y1 =
1 : ZA
Y1 =
1 0 j100.0974485 1 0 + j100.0974485 0 j100.0974485 0 + j100.0974485 0 + j100.0974485 02 + 100.0974485 2 0 + j100.0974485 10019 .4992
3 3
Y1 =
Y1 =
Y1 =
Y1 = +j 0.09924 0 09066
Siemens (Rectangular) Siemens (Polar)
OR
Y = .0 9 9 2 4 0 0 90 66 1 3 3 9 0
O
Admittance, Y2 =
1 : ZB
Y2 =
1 30 + j 40.05530633 1 30 j 40.05530633 30 + j 40.05530633 30 j 40.05530633 30 j 40.05530633 30 2 + 40.05530633 2 30 j 40.05530633 2504.427565
6 0.05977 j 19391
Y2 =
Y2 =
Y2 =
Y2 = .01775 0 19882
Siemens (Rectangular)
O
OR
Y2 = .09833 0 19 2 1 2 5 .1895 3 6046
Siemens (Polar)
23
Brendan Burr BTEC Higher National Certificate in Electronics
Application of DC & AC Theory
Admittance, Y1 = 1 100
1 : ZA
Y3 =
Y3 = 0.01
Siemens (Rectangular) Siemens (Polar)
OR
Y3 =0.0 O 1 0
Current for BRANCH A, is given by: I A = V Y1 I A = 2000O 0.0099902646 3390O
I A = + 1.98596 0 j 9022
) (
Amps (Rectangular)
9 0
O
OR
I A = .9 8 5 9 6 1 9022
Amps (Polar)
Current BRANCH B, is given by: I B = V Y2 I B = 2000O 0.0199823132 53.16809456 O
I B = .20198 7 1007 1 .3557 j1 2486
) (
Amps (Rectangular)
O
OR
I B = .96 6 6 3 94 2 4 5 .1 8 9 5 3 6 0 4 6
Amps (Polar)
Current BRANCH C, is given by: I C = V Y3 I C = 2000O 0.010O
IC = 2
) (
Amps (Rectangular) Amps (Polar)
OR
I C = 2 O 0
24
Brendan Burr BTEC Higher National Certificate in Electronics
Application of DC & AC Theory
Total Admittance, Y = Y1 + Y2 + Y3 : Y = ( 0 + j 0.0099902646 33) + ( 0.0119787852 6 j 0.0159937971 ) + ( 0.01)
Y = .01775 0 29882 6 0.06052 j 00334 6 3
Siemens (Rectangular)
OR
Y = .02892 0 27375 5 .2721 1 7763
O
Siemens (Polar)
Total Current is given by: Total Current, I = V = VY Z I = 2000O 0.0227839725 15.27772613 O
) (
I = .35509 4 8774
1.20043 j 0769
Amps (Rectangular)
O
OR
I = .5695 4 574 5 .2721 1 7763
Amps (Polar)
Check:On the following Graph: The Red Waveform represents Total Current ( I ) in Polar. The Blue Waveform represents BRANCH A ( I A ) in Polar. The Magenta Waveform represents BRANCH B ( I B ) in Polar. The Dark Green Waveform represents BRANCH C ( I C ) in Polar.
25
Brendan Burr BTEC Higher National Certificate in Electronics
Application of DC & AC Theory
26
Brendan Burr BTEC Higher National Certificate in Electronics
Application of DC & AC Theory
Task 4
4.1 A 1kOhm resistor is connected across the secondary windings of an ideal transformer whose secondary voltage is 100 Volts. The current in the primary windings is 10mA. Draw a circuit diagram
(a)
Solution:-
(b)
Determine the secondary current
Solution:V2 = i2 RL i2 = V2 RL 100 1,000 Amps
i2 =
i2 = 0.1
27
Brendan Burr BTEC Higher National Certificate in Electronics
Application of DC & AC Theory
(c)
Determine the primary voltage
Solution:V1 N1 = V2 N 2 N1 1,000 = = 10 N2 100 V1 = 10 100 V1 = 10 100
V1 =1,0 0 0
Volts
(d)
Determine the transformer turns ratio
Solution:i2 N1 = =N i1 N 2 0.1 = 10 0.01 N = 10
N = 1 :1 0
28
Brendan Burr BTEC Higher National Certificate in Electronics
Application of DC & AC Theory
Check (Overall Circuit):-
29
Brendan Burr BTEC Higher National Certificate in Electronics
Application of DC & AC Theory
4.2
An ideal transformer has 1000 primary turns and 100 secondary turns. If the primary winding is connected to a 230V AC supply the secondary is connected to a 100 Ohms resistive load: Draw a circuit diagram
(a)
Solution:
(b)
Determine the secondary voltage
Solution: V1 N1 = V2 N 2 230 1,000 = V2 100 V2 = 230 10 Volts
V2 = 23
30
Brendan Burr BTEC Higher National Certificate in Electronics
Application of DC & AC Theory
(c)
Determine the secondary current
Solution: V2 = i2 RL 23 = i2 100
i 2 =0.2 3
Amps
(d)
Determine the power supplied in the primary circuit
Solution: POUT = PIN V2 i2 = V1 i1 23 0.23 = 230 i1 i1 = 23 0.23 230
i1 = 0.023 PIN = V1 i1 PIN = 230 0.023
P =5.2 9 IN
Watts
Check:PIN = POUT PIN = 230 0.023 = 5.29 POUT = 23 0.23 = 5.29
31
Brendan Burr BTEC Higher National Certificate in Electronics
Application of DC & AC Theory
Check (Overall Circuit):-
32
Brendan Burr BTEC Higher National Certificate in Electronics
Application of DC & AC Theory
Appendix 1
33
Brendan Burr BTEC Higher National Certificate in Electronics
Application of DC & AC Theory
Evaluation
This assignment required me to use existing knowledge of AC and DC Theories, to establish the answers when circuits are at certain conditions. Beginning with Task 1.1 with the two storage batteries, I felt that this Task went reasonably well. The question, for some reason appeared difficult at first as it was difficult to understand what the circuit looked like and what actually needed calculating. After much consideration I realised how the circuit should be put together and that the currents between the two batteries and the open circuit equivalent battery were required. Using Kirchhoffs Voltage and Current Laws, along with a general understanding of the circuit, I worked out equations for the two loops. I also worked out an equation for the currents, and using both, through superimposing and transposition, worked out the values for the currents. I checked Task 1.1 on Croc Clips and identical values for the currents were presented. This gave me the assurance that my answers were correct. For Task 1.2 I had to work out a specific current flowing through R4 (8 Ohms Resistor). This was done by splitting the original circuit into two and calculating each circuit with only one voltage source. I could then superimpose the two circuits onto one another and come up with an overall circuit diagram with each relevant current. I also checked Task 1.2 using Croc Clips, and the value for the current flowing through the 8 Ohms resistor was 319mA, which is exactly the same as I calculated. Moving onto Complex Waveforms, which we have been covering in other units, I found that Task 2 was relatively straight forward. It is very easy to generate a complex waveform when you know the equation, as you can enter it into Graphmatica, however this Task required me to use Microsoft Excel. This dragged the Task out for longer than was actually required as there was a lot of messing around required to get a waveform that can be generated in seconds elsewhere. The only thing that I can think of that is beneficial by doing it on Microsoft Excel is that you can see in the formula that you are adding the Harmonics to the Fundamental Waveform. I began to face a few problems when completing Task 3. This was mainly because of the AC condition and that the Check was difficult to follow because the waveforms were constantly moving and always out of phase with one another. For Task 3.1, I managed to get the individual Branch Currents and then using this I could calculate Overall Current being drawn from the supply. I done this by calculating the overall admittance and then multiplying it by the voltage, but this could also be done by adding the three currents together. For Task 3.2, this wasnt as simple. By calculating the overall admittance and then multiplying by the voltage I managed to get the Overall Current, which was represented in my check. However by adding the three currents, I did not receive the same result. I am still not sure why this is, but my guess would be that Branch A has zero resistance, which isnt realistic, therefore theoretically the overall calculation would be wrong, but through simulation you get the correct answer. I am confident my answers are correct, as my workings tie in extremely closely to the simulated results from Croc Clips. 34
Brendan Burr BTEC Higher National Certificate in Electronics
Application of DC & AC Theory
Finishing the assignment with Task 4, I felt that this Task went very quickly. I have already done similar problems to this through the EEP Unit and therefore could understand it immediately. I worked out each answer and checked them accordingly by using Croc Clips, this method was also used for my overall check as shown above.
Conclusion
To conclude, I am pleased with the outcome of this assignment. I am confident that I have correctly and appropriately answered the Tasks, due to my extensive checking methods. This assignment has also taken a lot of time to ensure it is accurate and I feel it meets the standard of my other two assignments in this Unit. I have received absolutely no help on this assignment, and will therefore be looking to achieve a good mark. I have one assignment left for this unit which is entirely research based and is already underway.
35
Brendan Burr BTEC Higher National Certificate in Electronics
Application of DC & AC Theory
Bibliography
Through guidance from my lecturer, the following text books, catalogues and websites I was able to complete this assignment: Books BTEC National Engineering (Mike Tooley & Lloyd Dingle) ISBN: 978-0-7506-8521-4 Success in Electronics (Tom Duncan & John Murray) ISBN: 0-7195-4015-1 Higher Engineering Mathematics (John Bird) ISBN: 0-7506-8152-7 Engineering Science (John Bird) ISBN: 0-7506-4991-7 Catalogues N/A Websites N/A
36
You might also like
- Volumetric Efficiency For Reciprocating CompressorDocument2 pagesVolumetric Efficiency For Reciprocating CompressorKrishna PATELNo ratings yet
- Applied CalculasDocument15 pagesApplied Calculasmohammad rashid tkNo ratings yet
- DC Generator CharacteristicsDocument10 pagesDC Generator CharacteristicsGideon MoyoNo ratings yet
- Coordinate Measuring MachineDocument7 pagesCoordinate Measuring MachineDivyanshuNo ratings yet
- BTEC HNC - Microprocessor Systems - Investigate Microprocessor Based SystemsDocument16 pagesBTEC HNC - Microprocessor Systems - Investigate Microprocessor Based SystemsBrendan BurrNo ratings yet
- Modelling and Finite Element Analysis of Elevator Buckets: January 2016Document9 pagesModelling and Finite Element Analysis of Elevator Buckets: January 2016Arief RachmanNo ratings yet
- OBJ + CONCLUSION BeltDocument1 pageOBJ + CONCLUSION BeltFattihiEkhmalNo ratings yet
- BTEC HNC - Electrical and Electronic Principles - Investigate Two Port NetworksDocument26 pagesBTEC HNC - Electrical and Electronic Principles - Investigate Two Port NetworksBrendan Burr100% (2)
- Theory of Machines Experiments Student ManualDocument28 pagesTheory of Machines Experiments Student ManualHoneyNo ratings yet
- MQA Lab ReportDocument15 pagesMQA Lab ReportMuhammad Waleed TariqNo ratings yet
- Mechanisms Report AnalysisDocument44 pagesMechanisms Report AnalysisOmar SaleemNo ratings yet
- BTEC HNC - Engineering Project - AllDocument155 pagesBTEC HNC - Engineering Project - AllBrendan Burr100% (5)
- Scissor LiftDocument8 pagesScissor LiftSiew Hiong JongNo ratings yet
- Problemas de EngranesDocument18 pagesProblemas de EngranesStratowarionNo ratings yet
- Electrical Measuring InstrumentsDocument25 pagesElectrical Measuring Instrumentsusman_uet08100% (1)
- Belt & Rope DrivesDocument26 pagesBelt & Rope Drivesarpit089100% (1)
- Mec 211 Autocad 1Document74 pagesMec 211 Autocad 1VietHungCao100% (1)
- BTEC HNC - Combinational and Sequential Logic - Design and Build Circuits Using Combinational LogicDocument16 pagesBTEC HNC - Combinational and Sequential Logic - Design and Build Circuits Using Combinational LogicBrendan BurrNo ratings yet
- FLUID POWER SYSTEMS Theory and PracticeDocument31 pagesFLUID POWER SYSTEMS Theory and PracticeRAMAR MNo ratings yet
- Metrology & Measurement: Anand K Bewoor & Vinay A KulkarniDocument23 pagesMetrology & Measurement: Anand K Bewoor & Vinay A KulkarniKuwer ThakurNo ratings yet
- Measurement of Length, Height & Diameter by Vernier Calipers, MicrometerDocument2 pagesMeasurement of Length, Height & Diameter by Vernier Calipers, MicrometerSarath TejaNo ratings yet
- Zeiss Ultra OptimeterDocument13 pagesZeiss Ultra OptimeterLokesh kumar MeenaNo ratings yet
- CAM-FOLLOWER MECHANICS AND DESIGNDocument61 pagesCAM-FOLLOWER MECHANICS AND DESIGNNauman KhanNo ratings yet
- Degree: B.E. Regulation: 2008 Branch: Mechanical Engineering Semester: 05 Duration: 3 Hours Max. Marks: 100Document48 pagesDegree: B.E. Regulation: 2008 Branch: Mechanical Engineering Semester: 05 Duration: 3 Hours Max. Marks: 100kaliappan45490No ratings yet
- Assemment BTEC HNDDocument11 pagesAssemment BTEC HNDaviNo ratings yet
- Electronics 1 Lab Manual PDFDocument30 pagesElectronics 1 Lab Manual PDFAnonymous 7y7TeR0% (1)
- Two Wheel Drive Forklift For Indusrial WarehousesDocument31 pagesTwo Wheel Drive Forklift For Indusrial WarehousesKalai SelvanNo ratings yet
- Alexander CH 03 Final R 1Document24 pagesAlexander CH 03 Final R 1GdeKomangFmoNo ratings yet
- Electric Vehicle Motor TypesDocument20 pagesElectric Vehicle Motor TypesRahulNo ratings yet
- Lect 1Document19 pagesLect 1Kong DuiDuiNo ratings yet
- SegmentationDocument51 pagesSegmentationAlbin Robin100% (1)
- ADJUST AND CALIBRATE HOME POSITION OF MECHANICAL ARMSDocument15 pagesADJUST AND CALIBRATE HOME POSITION OF MECHANICAL ARMSpauloNo ratings yet
- ME6701 Power Plant Engineering SyllabusDocument2 pagesME6701 Power Plant Engineering SyllabusSrinivasan Surendran100% (2)
- Security Lock ProjectDocument13 pagesSecurity Lock Projecttaha199No ratings yet
- Fluid StaticsDocument57 pagesFluid StaticsTaha Zafar100% (1)
- Micro ActuatorsDocument10 pagesMicro ActuatorsEyad A. FeilatNo ratings yet
- Internal Attachment Technical Report 2021-1Document22 pagesInternal Attachment Technical Report 2021-1Josline Muriiki100% (1)
- DC Motor ArduinoDocument40 pagesDC Motor ArduinoBodo De La BuernoNo ratings yet
- Polyphase Ac CircuitsDocument18 pagesPolyphase Ac CircuitsRay YudaNo ratings yet
- Electronics Lab Manual: Schedule & Experiment No. (Title) Tentative WeekDocument6 pagesElectronics Lab Manual: Schedule & Experiment No. (Title) Tentative Weekabubakarsha100% (1)
- Project ReportDocument15 pagesProject ReportPrakhar AgrawalNo ratings yet
- Coulomb's Law MC Questions PDFDocument7 pagesCoulomb's Law MC Questions PDFLynn Hollenbeck BreindelNo ratings yet
- BTEC HNC - Science - Analyse Dynamic Engineering SystemsDocument15 pagesBTEC HNC - Science - Analyse Dynamic Engineering SystemsBrendan BurrNo ratings yet
- Group 15 EMD332 Machine Design Report - 2D Camera SliderDocument33 pagesGroup 15 EMD332 Machine Design Report - 2D Camera SliderMark SelvanNo ratings yet
- Kinematics of a slider-crank mechanism experimentDocument22 pagesKinematics of a slider-crank mechanism experimentSmart100% (1)
- Hoisting EquipmentDocument56 pagesHoisting EquipmentbroNo ratings yet
- Assignment: A and A Wheel WeighingDocument1 pageAssignment: A and A Wheel WeighingIshfaqurNo ratings yet
- 6 - Sequential Applications - TeoríaDocument71 pages6 - Sequential Applications - Teoríabob_892252733No ratings yet
- 2robot Applications Main8Document55 pages2robot Applications Main8saikumarNo ratings yet
- IJIRAE::Design and DMU Kinematic Analysis of Slider Crank Mechanism Using CATIA and MATLABDocument6 pagesIJIRAE::Design and DMU Kinematic Analysis of Slider Crank Mechanism Using CATIA and MATLABIJIRAE- International Journal of Innovative Research in Advanced EngineeringNo ratings yet
- Cim Automation Lab Manual 10me78Document57 pagesCim Automation Lab Manual 10me78chandrashekar mNo ratings yet
- Linear Induction Motor ExplainedDocument3 pagesLinear Induction Motor ExplainedMakkal ThalaivanNo ratings yet
- Explain Quick Return Mechanism PDFDocument2 pagesExplain Quick Return Mechanism PDFKelly0% (1)
- Adjust eight-wheel trolley wheels with ZPMC documentDocument3 pagesAdjust eight-wheel trolley wheels with ZPMC documenttest testtNo ratings yet
- GEARS FUNdaMENTALS of Design Topic 6 PDFDocument62 pagesGEARS FUNdaMENTALS of Design Topic 6 PDFCristina Andreea CrissyNo ratings yet
- Slider CrankDocument3 pagesSlider CrankAnonymous GGtvR65MR100% (1)
- BTEC HNC - Electronics - Investigate Circuits With FeedbackDocument23 pagesBTEC HNC - Electronics - Investigate Circuits With FeedbackBrendan BurrNo ratings yet
- Lab. 1: RLC Circuits: 1.1. List All The Resistance Values (Sorted in The Accending Order)Document6 pagesLab. 1: RLC Circuits: 1.1. List All The Resistance Values (Sorted in The Accending Order)Thịnh Lý HưngNo ratings yet
- Transformer Lab Experiment GuideDocument7 pagesTransformer Lab Experiment GuideOve KhanNo ratings yet
- Electromagnetic Compatibility (EMC) Design and Test Case AnalysisFrom EverandElectromagnetic Compatibility (EMC) Design and Test Case AnalysisNo ratings yet
- BTEC HNC - Electronics - Investigate Signals and NoiseDocument21 pagesBTEC HNC - Electronics - Investigate Signals and NoiseBrendan BurrNo ratings yet
- BTEC HNC - Engineering Project - AllDocument155 pagesBTEC HNC - Engineering Project - AllBrendan Burr100% (5)
- BTEC HNC - Engineering Design - Prepare A Design SpecificationDocument12 pagesBTEC HNC - Engineering Design - Prepare A Design SpecificationBrendan Burr100% (10)
- BTEC HNC - Control Systems and Automation - Equations To Determine System ParametersDocument37 pagesBTEC HNC - Control Systems and Automation - Equations To Determine System ParametersBrendan BurrNo ratings yet
- BTEC HNC - Control Systems and Automation - Use Laplace Transforms To Determine System ParametersDocument24 pagesBTEC HNC - Control Systems and Automation - Use Laplace Transforms To Determine System ParametersBrendan BurrNo ratings yet
- BTEC HNC - Control Systems and Automation - Use Analytical Techniques To Form Models of Systems and ProcessesDocument43 pagesBTEC HNC - Control Systems and Automation - Use Analytical Techniques To Form Models of Systems and ProcessesBrendan BurrNo ratings yet
- BTEC HNC - Business Systems - Financial Planning and ControlDocument13 pagesBTEC HNC - Business Systems - Financial Planning and ControlBrendan BurrNo ratings yet
- BTEC HNC - Control Systems and Automation - Examine Process Controllers Using Control PhilosophiesDocument13 pagesBTEC HNC - Control Systems and Automation - Examine Process Controllers Using Control PhilosophiesBrendan BurrNo ratings yet
- BTEC HNC - Electronics - Investigate Types of AmplifierDocument19 pagesBTEC HNC - Electronics - Investigate Types of AmplifierBrendan BurrNo ratings yet
- BTEC HNC - Business Systems - Select and Apply Costing Systems and TechniquesDocument11 pagesBTEC HNC - Business Systems - Select and Apply Costing Systems and TechniquesBrendan BurrNo ratings yet
- BTEC HNC - Science - Analyse Static Engineering SystemsDocument23 pagesBTEC HNC - Science - Analyse Static Engineering SystemsBrendan BurrNo ratings yet
- BTEC HNC - Business Systems - Manage Work Activities To Achieve Organisational ObjectivesDocument19 pagesBTEC HNC - Business Systems - Manage Work Activities To Achieve Organisational ObjectivesBrendan Burr50% (2)
- BTEC HNC - Business Systems - Applied Project Planning and Scheduling Methods For A ProjectDocument13 pagesBTEC HNC - Business Systems - Applied Project Planning and Scheduling Methods For A ProjectBrendan BurrNo ratings yet
- BTEC HNC - Electrical and Electronic Principles - Investigate Transients in RLC CircuitsDocument20 pagesBTEC HNC - Electrical and Electronic Principles - Investigate Transients in RLC CircuitsBrendan BurrNo ratings yet
- BTEC HNC - Science - Investigate Information and Energy Control SystemsDocument28 pagesBTEC HNC - Science - Investigate Information and Energy Control SystemsBrendan BurrNo ratings yet
- BTEC HNC - Science - Analyse Dynamic Engineering SystemsDocument15 pagesBTEC HNC - Science - Analyse Dynamic Engineering SystemsBrendan BurrNo ratings yet
- BTEC HNC - Analytical Methods - CalculusDocument43 pagesBTEC HNC - Analytical Methods - CalculusBrendan BurrNo ratings yet
- BTEC HNC - Electronics - Investigate Circuits With FeedbackDocument23 pagesBTEC HNC - Electronics - Investigate Circuits With FeedbackBrendan BurrNo ratings yet
- BTEC HNC - Electrical and Electronic Principles - Investigate Two Port NetworksDocument26 pagesBTEC HNC - Electrical and Electronic Principles - Investigate Two Port NetworksBrendan Burr100% (2)
- BTEC HNC - Electrical and Electronic Principles - Investigate Circuit TheoryDocument38 pagesBTEC HNC - Electrical and Electronic Principles - Investigate Circuit TheoryBrendan BurrNo ratings yet
- BTEC HNC - Electrical and Electronic Principles - Investigate Complex WavesDocument21 pagesBTEC HNC - Electrical and Electronic Principles - Investigate Complex WavesBrendan BurrNo ratings yet
- BTEC HNC - Analytical Methods - Trigonometric MethodsDocument34 pagesBTEC HNC - Analytical Methods - Trigonometric MethodsBrendan Burr100% (1)
- BTEC HNC - Analytical Methods - Algebraic MethodsDocument41 pagesBTEC HNC - Analytical Methods - Algebraic MethodsBrendan Burr100% (1)
- BTEC HNC - Combinational and Sequential Logic - Design and Build Circuits Using Combinational LogicDocument16 pagesBTEC HNC - Combinational and Sequential Logic - Design and Build Circuits Using Combinational LogicBrendan BurrNo ratings yet
- BTEC HNC - Analytical Methods - Statistics and ProbabilityDocument20 pagesBTEC HNC - Analytical Methods - Statistics and ProbabilityBrendan Burr50% (2)
- BTEC NC - Further Maths For Technicians - Applied Trigonometric TechniquesDocument5 pagesBTEC NC - Further Maths For Technicians - Applied Trigonometric TechniquesBrendan BurrNo ratings yet
- BTEC NC - Further Mathematics For Technicians - Applied Algebraic and Graphical TechniquesDocument14 pagesBTEC NC - Further Mathematics For Technicians - Applied Algebraic and Graphical TechniquesBrendan Burr100% (1)
- BTEC NC - Further Mathematics For Technicians - Applied CalculusDocument15 pagesBTEC NC - Further Mathematics For Technicians - Applied CalculusBrendan BurrNo ratings yet
- MM-Powerinfo Vol 1Document41 pagesMM-Powerinfo Vol 1ravi196No ratings yet
- CP 23: 2000 Formwork Design CodeDocument34 pagesCP 23: 2000 Formwork Design CodeShumei Zhou100% (1)
- Reynolds Tubing Parts List 2014Document9 pagesReynolds Tubing Parts List 2014Pato Patiño MuñozNo ratings yet
- ABAP Test 1. Full Buffering Would Be Appropriate ForDocument9 pagesABAP Test 1. Full Buffering Would Be Appropriate ForHemadri NaiduNo ratings yet
- Fiber Optic Cable GuideDocument5 pagesFiber Optic Cable GuideMaharudraMahajanNo ratings yet
- ID09011 B 0281290596Document76 pagesID09011 B 0281290596rajeshdod1No ratings yet
- 78DXXL: Unisonic Technologies Co., LTDDocument8 pages78DXXL: Unisonic Technologies Co., LTDSlava VanatNo ratings yet
- List Scs SadcDocument4 pagesList Scs SadcDhananjayan GopinathanNo ratings yet
- Gujarat Technological UniversityDocument2 pagesGujarat Technological UniversityRishabh TalujaNo ratings yet
- Google Advertising Fully Solved TestDocument10 pagesGoogle Advertising Fully Solved TestfanegarajNo ratings yet
- Harish Kumar Banga. Rajesh Kumar. Parveen Kalra. Rajendra M. Belokar - Additive Manufacturing With Medical Applications-CRC Press (2022)Document340 pagesHarish Kumar Banga. Rajesh Kumar. Parveen Kalra. Rajendra M. Belokar - Additive Manufacturing With Medical Applications-CRC Press (2022)Piotr JankowskiNo ratings yet
- Mistake-proofing techniques to avoid errorsDocument40 pagesMistake-proofing techniques to avoid errorssuresh84123No ratings yet
- Lecture14 ClusteringDocument50 pagesLecture14 ClusteringindiraNo ratings yet
- Box PushingDocument4 pagesBox PushingNArendra REddy100% (3)
- Motion Control Portfolio Overview Customer May2020 PDFDocument41 pagesMotion Control Portfolio Overview Customer May2020 PDFLuis Hoyos Bautista100% (1)
- Pos.14 - Hydrokraft Piston Pump - PVW - 2016Document73 pagesPos.14 - Hydrokraft Piston Pump - PVW - 2016Дмитрий МазуренкоNo ratings yet
- Technical Data: NPN Power Silicon TransistorDocument2 pagesTechnical Data: NPN Power Silicon TransistorJuan RamírezNo ratings yet
- Sigma-5 Positioner Manual: MH (T) - SeriesDocument60 pagesSigma-5 Positioner Manual: MH (T) - SeriesRex BernedoNo ratings yet
- Mil STD 781C PDFDocument136 pagesMil STD 781C PDFgiovannobgNo ratings yet
- Experiment 1-2 Three-Phase Half Controlled Converter PDFDocument2 pagesExperiment 1-2 Three-Phase Half Controlled Converter PDFRAJENDRA KUMAWATNo ratings yet
- Evaluation of Non-Chemical Treatment Technologies For Cooling Towers at Select California FacilitiesDocument68 pagesEvaluation of Non-Chemical Treatment Technologies For Cooling Towers at Select California FacilitiesCarlos GamarraNo ratings yet
- Scholar Peter Senge PresentationDocument29 pagesScholar Peter Senge PresentationShahmien SevenNo ratings yet
- Design of Left Hand Side Abutment for Bridge CalculationDocument53 pagesDesign of Left Hand Side Abutment for Bridge Calculationmanoj_structureNo ratings yet
- Energex Commercial and Industrial PMT App ADocument8 pagesEnergex Commercial and Industrial PMT App AdseugenioNo ratings yet
- PascalDocument3 pagesPascalsenthilgnmitNo ratings yet
- FieldGenius 7 SP1 Release NotesDocument2 pagesFieldGenius 7 SP1 Release NotesGabriel MendozaNo ratings yet
- ABAP Objects - Exercise 1 - Classes and Objects (Global)Document7 pagesABAP Objects - Exercise 1 - Classes and Objects (Global)Joyce Pereira0% (1)
- Manage Information SystemsDocument13 pagesManage Information SystemsNayra DizonNo ratings yet
- Catalogue - Single - Three - Phase LAFERTDocument101 pagesCatalogue - Single - Three - Phase LAFERTAleex RodriguezNo ratings yet
- Design Input - Pressure Reducing ValveDocument8 pagesDesign Input - Pressure Reducing ValvekausikrNo ratings yet