Professional Documents
Culture Documents
Chapter 13
Uploaded by
6951089Original Description:
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Chapter 13
Uploaded by
6951089Copyright:
Available Formats
Market Structure
Cartels (cooperative oligopoly models / collusion) Firms agree to restrict output & act like a monopoly illegal some cartels persist SA examples? incentives to (1) collude; (2) cheat on agreement. Firms gain by acting together like a monopoly (output & price). Only works if all act together The less elastic market DD, the higher p and benefits from forming the cartel.
Favourable conditions for emergence of cartels: small no. of large firms geographically close homogenous products difficult entry similar cost levels. Cartels will fail if: non-member firms can supply substitutes; member firms cheat. Noncooperative oligopoly: Cournot (firms act simultaneously) Stackelberg (one firm can act first) Cournot model non-cooperative simultaneous decisions imperfect info choose Q level Assume: 2 firms, & no others can enter Identical products One market period, & product cannot be stored for sale later. Each firms DD = total DD other firms output
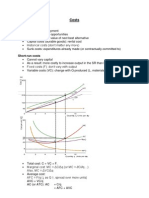
Graph a: If American were a monopoly, American demand curve would be the market demand curve D. To maximise profit : American would set output so that MR intersects MC Which is 96 thousand passengers per quarter & the monopoly price is $243(the price is read above). Graph b: Duopoly: An oligopoly with two firms. American demand curve is not the entire market demand curve as it needs to consider Uniteds actions. American is only concerned about and transports residual demand. Residual demand calculation: Q qu (Total quantity-united quantity) If the price is $211, total quantity is 128; united flies 64....therefore American would fly 64. To maximise its profit American sets its output so that MR corresponds to MC & residual = MC.
American will sell a monopoly number of tickets 96 if united flies no passengers. The negative slope shows that American sells fewer tickets the more people American thinks that united will fly. Counot equilibrium (qa =qu =64).
Graphical approach: (market DD, residual DD, best-response curves) Algebraic approach to Cournot: Market DD: Q = 339 p MC = AC = $147 Americans residual DD: qA = Q qU = 339 p qU p = 339 qA qU MRr = 339 2qA qU Americans best-response: MRr = MC MRr = 339 2qA qU = MC = 147 339 2qA qU = 147 qA = (339 147) qU qA = 96 qU Uniteds best-response: qU = 96 qA Cournot eqm: solve the eqns simultaneously: qA = 96 (96 qA) qA = 64 qU = 64 Total output Q = qA + qU = 128 Substing into Q = 339 p, p = $211. Comparisons of outcomes In the Stackelburg model the leader produces twice as much as the follower. In the Stackelburg model output is generally higher and prices are generally lower therefore consumers prefer the Stackelburg equilibrium to the Counot equilibrium. Total Stackelburg model profit is lower because the follower usually earns less profit.
Stackelberg model One firm (the leader) is able to set its output before its rival/s (the follower/s). (Leader works out followers best-response curve.)
Residual DD & best-response curves when firms can choose any output level. E.g. American Airlines is able to act first. Dr = market DD qU (see Uniteds best-response curve) MRr = MC to find eqm P & qA; United will then produce qU determined by qA. Note: Firms ability to move first is essential (just announcing intended output not a credible threat) Important for strategic trade policy in real world. Problems with intervention: If the government wants to subsidise a domestic firm to produce the same output as it would if it were a Stackelburg leader 5 conditions must hold: The government must be able to set its subsidy before firms choose their output level. Other governments must not retaliate. Governments actions must be credible. The governments must know enough about how firms behave to intervene. The government must know all relevant facts about firms, including whether they are setting quantities.
Bertrand price-setting model: Monop comp or oligopoly Firms set p & let consumers decide on Q. Bertrand eqm: set of prices such that no firm can obtain a higher profit by choosing a different price if the other firms continue to charge these prices. Eqm different to Cournot and depends on whether firms sell identical or differentiated products.
With identical products: p = MC. e.g. 2 firms, constant MC & AC of $5/unit. Firm 2 charges p = $10. What p should Firm 1 set? (Its best response?) For any p > MC & AC Firm 2 charges, best response for Firm 1 is to undercut it slightly. (If Firm 2 charges p < $5, Firm 1 wont produce at all.) Best-response curves With identical products, p = MC; Bertrand eqm = perf compettv eqm. Cournot eqm: p = MC/ 1 + 1/(n) = $5 / 1 + 1 / (n). If = -1 and n = 2, p = $10. Bertrand unrealistic with identical products: Small no. firms 0 profit? Price unaffected by DD or no. of firms.
Bertrand eqm with differentiated products:
Each firm doesnt have to match rivals price cut exactly. Best-response curves for Coke & Pepsi. Firms can charge p > MC because of product differentiation.
N.B. Diffn depends on consumers perceptions. Effects of diffn on price: higher (less substitutable less elastic DD) Effects on welfare: although p > MC, welfare is not necessarily lower; consumers value variety & may gain utility (CS) from new brands. Monopolistic competition Free entry LR, only normal profits Each firm faces downsloping residual DD, so p > MC, because relatively few firms, or differentiated products. No. of firms: Each firms elasticity = n EoS and size of market DD determine how many firms the market can accommodate. Differentiated products: Firm charging slightly higher p will not lose all customers (market power).
Monop comp eqm: MR = MC; p = AC (but p > MC) Smallest Q at which AC curve reaches its minimum: full capacity or minimum efficient scale (here firm is reaping max poss EoS). A monop comp firm always operates at less than full capacity in the LR. Fixed costs & the no. of firms: Larger FC smaller no. of firms With airline example: MC = $147 / passenger; AC = 147 + F/q; F = $2.3m.
You might also like
- Chapter 17Document5 pagesChapter 176951089No ratings yet
- Chapter 7Document5 pagesChapter 76951089No ratings yet
- Chapter 5Document9 pagesChapter 56951089No ratings yet
- Chapter 4Document6 pagesChapter 46951089No ratings yet
- Shoe Dog: A Memoir by the Creator of NikeFrom EverandShoe Dog: A Memoir by the Creator of NikeRating: 4.5 out of 5 stars4.5/5 (537)
- The Yellow House: A Memoir (2019 National Book Award Winner)From EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Rating: 4 out of 5 stars4/5 (98)
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeFrom EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeRating: 4 out of 5 stars4/5 (5794)
- The Little Book of Hygge: Danish Secrets to Happy LivingFrom EverandThe Little Book of Hygge: Danish Secrets to Happy LivingRating: 3.5 out of 5 stars3.5/5 (400)
- Grit: The Power of Passion and PerseveranceFrom EverandGrit: The Power of Passion and PerseveranceRating: 4 out of 5 stars4/5 (588)
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureFrom EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureRating: 4.5 out of 5 stars4.5/5 (474)
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryFrom EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryRating: 3.5 out of 5 stars3.5/5 (231)
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceFrom EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceRating: 4 out of 5 stars4/5 (895)
- Team of Rivals: The Political Genius of Abraham LincolnFrom EverandTeam of Rivals: The Political Genius of Abraham LincolnRating: 4.5 out of 5 stars4.5/5 (234)
- Never Split the Difference: Negotiating As If Your Life Depended On ItFrom EverandNever Split the Difference: Negotiating As If Your Life Depended On ItRating: 4.5 out of 5 stars4.5/5 (838)
- The Emperor of All Maladies: A Biography of CancerFrom EverandThe Emperor of All Maladies: A Biography of CancerRating: 4.5 out of 5 stars4.5/5 (271)
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaFrom EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaRating: 4.5 out of 5 stars4.5/5 (266)
- On Fire: The (Burning) Case for a Green New DealFrom EverandOn Fire: The (Burning) Case for a Green New DealRating: 4 out of 5 stars4/5 (74)
- The Unwinding: An Inner History of the New AmericaFrom EverandThe Unwinding: An Inner History of the New AmericaRating: 4 out of 5 stars4/5 (45)
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersFrom EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersRating: 4.5 out of 5 stars4.5/5 (345)
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyFrom EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyRating: 3.5 out of 5 stars3.5/5 (2259)
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreFrom EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreRating: 4 out of 5 stars4/5 (1090)
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)From EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Rating: 4.5 out of 5 stars4.5/5 (121)
- Her Body and Other Parties: StoriesFrom EverandHer Body and Other Parties: StoriesRating: 4 out of 5 stars4/5 (821)
- Auditing A Business Risk Approach 8th Edition Rittenberg Test BankDocument39 pagesAuditing A Business Risk Approach 8th Edition Rittenberg Test BankWilliamMcphersonmifzjNo ratings yet
- Commercial Law DigestsDocument4 pagesCommercial Law DigestsAnn SCNo ratings yet
- Regulation of Partition FencesDocument3 pagesRegulation of Partition FencesRobert MenschNo ratings yet
- Basel 1 NormsDocument12 pagesBasel 1 NormsamolreddiwarNo ratings yet
- FAA FOIA Logs For April and May 2013Document78 pagesFAA FOIA Logs For April and May 2013Trent SeibertNo ratings yet
- PaperforRecyclingQuality Control GuidelinesWITHANNEX - (Are La Baza EN643)Document14 pagesPaperforRecyclingQuality Control GuidelinesWITHANNEX - (Are La Baza EN643)Violeta&Florin GasparNo ratings yet
- The Reliance of External Audit On Internal Audit WorkDocument65 pagesThe Reliance of External Audit On Internal Audit WorkHassan ShataNo ratings yet
- Doctrine of CaveatDocument4 pagesDoctrine of CaveatShahjahan DashtiNo ratings yet
- Joining LetterDocument4 pagesJoining LetterHarshit TandonNo ratings yet
- Managing Cyber Security V1 (Level-3)Document20 pagesManaging Cyber Security V1 (Level-3)venky_akella100% (2)
- Personnel and Payroll Questionnaire: Yes No N/A RemarksDocument4 pagesPersonnel and Payroll Questionnaire: Yes No N/A RemarksMeghashyam RamanujamNo ratings yet
- Final Reviewer LegalDocument12 pagesFinal Reviewer LegalnairajaneNo ratings yet
- Draft - SOP - Scrap SalesDocument9 pagesDraft - SOP - Scrap SalesDeepak BabelNo ratings yet
- R03.3 Guidance For Standard IIDocument15 pagesR03.3 Guidance For Standard IIBảo TrâmNo ratings yet
- Definition of Securities Under Securities Contract Regulation ActDocument40 pagesDefinition of Securities Under Securities Contract Regulation ActYunus Worn Out'sNo ratings yet
- Divinagracia Vs Consolidated Broadcasting System, Inc., GR No. 162272, April 7, 2009Document27 pagesDivinagracia Vs Consolidated Broadcasting System, Inc., GR No. 162272, April 7, 2009Noreen Joyce J. Pepino100% (2)
- Vinnik FincenDocument20 pagesVinnik FincenAnonymous QbU0qGmoU5No ratings yet
- Saveetha School of Law Law Relating To Financial Marketing Regulation and Competition Law Question Bank PART - A (4 Marks)Document2 pagesSaveetha School of Law Law Relating To Financial Marketing Regulation and Competition Law Question Bank PART - A (4 Marks)Amudha MonyNo ratings yet
- Digested Cases in Taxation I, Part 1Document35 pagesDigested Cases in Taxation I, Part 1lonitsuaf89% (9)
- SurveyDocument2 pagesSurveyRhuejane Gay MaquilingNo ratings yet
- Indian Company Law Regulates The Corporations Formed Under The Section 2Document9 pagesIndian Company Law Regulates The Corporations Formed Under The Section 2nitin0010No ratings yet
- Notice: Agency Information Collection Activities Proposals, Submissions, and ApprovalsDocument2 pagesNotice: Agency Information Collection Activities Proposals, Submissions, and ApprovalsJustia.comNo ratings yet
- 5Document16 pages5abadi gebruNo ratings yet
- Form 301-General Information (Application For Registration of A Foreign For-Profit Corporation)Document7 pagesForm 301-General Information (Application For Registration of A Foreign For-Profit Corporation)wavy2gravyNo ratings yet
- Attorney Tax Business Editor in Portland OR Resume Lauren BotneyDocument2 pagesAttorney Tax Business Editor in Portland OR Resume Lauren BotneyLaurenBotneyNo ratings yet
- Guidelines On PD and LGD Estimation (EBA-GL-2017-16) - Chapters 1,2,3 (Only PD Estimation Part) PDFDocument200 pagesGuidelines On PD and LGD Estimation (EBA-GL-2017-16) - Chapters 1,2,3 (Only PD Estimation Part) PDFShankar RavichandranNo ratings yet
- Ivs 2017Document18 pagesIvs 2017Gunjan RajdevNo ratings yet
- Reblex AnswersDocument17 pagesReblex AnswersAerol BuenaventuraNo ratings yet
- Ashurst Global Guide To Public M and A 2020Document114 pagesAshurst Global Guide To Public M and A 2020Matias HermosillaNo ratings yet
- Finance and Economics Discussion Series Divisions of Research & Statistics and Monetary Affairs Federal Reserve Board, Washington, D.CDocument41 pagesFinance and Economics Discussion Series Divisions of Research & Statistics and Monetary Affairs Federal Reserve Board, Washington, D.CTBP_Think_TankNo ratings yet