Constitutive Models Relations between Stress and Strain

The equations listed in Chapter 2 are universal they apply to all deformable solids. They cant be solved, however, unless the deformation measure can be related to the internal forces. The constitutive model for a material is a set of equations relating stress to strain (and possibly strain history, strain rate, and other field quantities). Unlike the governing equations in the previous chapter, these equations cannot generally be calculated using fundamental physical laws (although people are trying to do this). Instead, constitutive models are fit to experimental measurements. Before discussing specific constitutive models, it is helpful to review the basic assumptions that we take for granted in developing stress-strain laws. They are listed below. A very small sample that is extracted from the solid has uniform properties; When the solid is deformed, initially straight lines in the solid are deformed into smooth curves (with continuous slope); This means that very short line segments (much shorter than the radius of curvature of the curves) are just stretched and rotated by the deformation. Consequently, the deformation of a sufficiently small volume element can be characterized by the deformation gradient; The stress at a point in the solid depends only on the change in shape of a vanishingly small volume element surrounding the point. It must therefore be a function of the deformation gradient or a strain measure that is derived from it. If we accept the preceding assumptions, it means that we can measure the relationship between stress and strain by doing an experiment that induces a uniform strain in a suitable sample of the material. According to our assumptions, the stress should also be uniform, and can be calculated from the forces acting on the specimen. These are clearly approximations. Materials are not really uniform at small scales, whether you choose to look at the atomic scale, or the microstructural scale. However, these features are usually much smaller than the size of the solid part or component, and the material can be regarded as statistically uniform, in the sense that if you cut two specimens with similar size out of the material they will behave in the same way. A continuum model then describes the average stress and deformation in a region of the material that is larger than microstructural features, but small compared with the dimensions of the part.

3.1 General requirements for constitutive equations

You may be called upon to develop a stress-strain law for a new material at some point of your career. If so, it is essential to make sure that the stress-strain law satisfies two conditions: (i) It must obeys the laws of thermodynamics. (ii) It must satisfy the condition of objectivity, or material frame indifference. In addition, it is a good idea to ensure that the material satisfies the Drucker stability criterion discussed in more detail below. Of course, your proposed law must conform to experimental measurements, and if possible should be based on some understanding of the physical processes that govern the response of the solid. Thermodynamic restrictions: The laws of thermodynamics impose two restrictions on stressstrain laws: 1. The first law requires that the work done by stresses must either be stored as recoverable internal energy in the solid, or be dissipated as heat (or a combination of both). 2. The second law requires that if a sample of the material is subjected to a cycle of deformation that starts and ends with an identical strain and internal energy (at constant temperature, or without heat exchange with the surroundings) the total work done must be positive or zero. Objectivity: Strictly speaking, the term objectivity or material frame independence is the condition that the tensor-valued functions that relate stress to deformation measure must transform correctly under a change of basis and change of origin for the coordinate system. A detailed mathematical derivation of the consequences of objectivity will not be given here (see for example Malvern Introduction to the Mechanics of a Continuous Medium, Prentice Hall). However, you can check whether a constitutive law is objective using the following simple (analytical) test: 1. Load the solid (quasi-statically) by subjecting its boundary to prescribed forces, to induce

a Cauchy stress in the solid. 2. Subject both the solid, and the loads acting on the solid, to a quasi-static rigid rotation, characterized by a rotation tensor . 3. The constitutive law must predict that after the rotation, the stress components change to new values given by To see this, note that since the loads rotate together with the solid, the components of traction acting normal and tangent to any interior material plane in the solid must remain constant. With this in mind: 1. Suppose that, just before the rotation is applied, denotes the traction acting on an interior material plane with normal . 2. The traction vector and the normal to the interior plane rotate with the solid, and have components after rotation.

therefore and

3.

By definition,

From (2), we see

therefore that 4. Multiply both sides of this equation by to see that and recall that

5.

Comparing this with (1), we conclude that . Finally, multiplying both sides of this equation by

we conclude that required result.

, giving the

Drucker Stability: For most practical applications, the constitutive equation must satisfy a condition known as the Drucker stability criterion, which can be expressed as follows. Consider a deformable solid, subjected to boundary tractions displacement field . Suppose that the tractions are increased to through the displacements resulting in an additional displacement sense of Drucker if the work done by the tractions is positive or zero for all : , which induce some ,

. The material is said to be stable in the

You can show that this condition is satisfied as long as the stress-strain relation obeys

where and

is

the

change

in

Kirchhoff

stress,

is an increment in strain resulting from an infinitesimal change in displacement .

This is not a thermodynamic law (the work done by the change in tractions is not a physically meaningful quantity), and there is nothing to say that real materials have to satisfy Drucker stability. In fact, many materials show clear signs that they are not stable in the sense of Drucker. However, if you try to solve a boundary value problem for a material that violates the Drucker stability criterion, you are likely to run into trouble. The problem will probably

not have a unique solution, and in addition you are likely to find that smooth curves on the undeformed solid develop kinks (and may not even be continuous) after the solid is deformed. This kind of deformation violates one of the fundamental assumptions underlying continuum constitutive equations. A simple example of a stress-strain curve for material that is not stable in the sense of Drucker is shown in the picture. The stability criterion is violated wherever the stress decreases with strain in tension, or increases with strain in compression. For the former we see that latter , while , while . ; for the

In the following chapter, we outline constitutive laws that were developed to approximate the behavior of a wide range of materials, including polycrystalline metals and nonmetals; elastomers; polymers; biological tissue; soils; and metal single crystals. A few additional material models, which account for material failure

3.2 Linear elastic material behavior

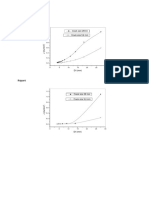
You are probably familiar with the behavior of a linear elastic material from introductory materials courses. 3.2.1 Isotropic, linear elastic material behavior If you conduct a uniaxial tensile test on almost any material, and keep the stress levels sufficiently low, you will observe the following behavior: The specimen deforms reversibly: If you remove the loads, the solid returns to its original shape. The strain in the specimen depends only on the stress applied to it it doesnt depend on the rate of loading, or the history of loading. For most materials, the stress is a linear function of strain, as shown in the picture above. Because the strains are small, this is true whatever stress measure is adopted (Cauchy stress or nominal stress), and is true whatever strain measure is adopted (Lagrange strain or infinitesimal strain). For most, but not all, materials, the material has no characteristic orientation. Thus, if you cut a tensile specimen out of a block of material, as shown in the figure, the the stress strain curve will be independent of the orientation of the specimen relative to the block of material. Such materials are said to be isotropic. If you heat a specimen of the material, increasing its temperature uniformly, it will generally change its shape slightly. If the material is isotropic (no preferred material orientation) and homogeneous, then the specimen will simply increase in size, without shape change.

3.2.2 Stress strain relations for isotropic, linear elastic materials. Youngs Modulus, Poissons ratio and the Thermal Expansion Coefficient. Before writing down stress strain relations, we need to decide what strain and stress measures we want to use. Because the model only works for small shape changes Deformation is characterized using the infinitesimal strain tensor defined in Section 2.1.7. This is convenient for calculations, but has the disadvantage that linear elastic constitutive equations can only be used if the solid experiences small rotations, as well as small shape changes. All stress measures are taken to be equal. We can use the Cauchy stress the stress measure. as

You probably already know the stress strain relations for an isotropic, linear elastic solid. They are repeated below for convenience.

Here, E and are Youngs modulus and Poissons ratio, is the coefficient of thermal expansion, and is the increase in temperature of the solid. The remaining relations can be deduced from the fact that both symmetric. The inverse relationship can be expressed as and are

HEALTH WARNING: Note the factor of 2 in the strain vector. Most texts, and most FEM codes use this factor of two, but not all. In addition, shear strains and stresses are often listed in a different order in the strain and stress vectors. For isotropic materials this makes no difference, but you need to be careful when listing material constants for anisotropic materials (see below). We can write this expression in a much more convenient form using index notation. Verify for yourself that the matrix expression above is equivalent to

The inverse relation is

The stress-strain relations are often expressed using the elastic modulus tensor or the elastic compliance tensor as

In terms of elastic constants,

and

are

3.2.3 Reduced stress-strain equations for plane deformation of isotropic solids For plane strain or plane stress deformations, some strain or stress components are always zero (by definition) so the stress-strain laws can be simplified.

For

plane

strain

deformation

. The stress strain laws are therefore

In index notation

where Greek subscripts For a plane stress deformation

can have values 1 or 2.

3.2.4 Representative values for density, and elastic constants of isotropic solids Most of the data in the table below were taken from the excellent introductory text `Engineering Materials, by M.F. Ashby and D.R.H. Jones, Pergamon Press. The remainder are from random web pages Note the units values of E are given in ; the G stands for Expansion coeft

Giga, and is short for . The units for density are in thats Mega grams. One mega gram is 1000 kg. Material Mass density Youngs Modulus Poisson Ratio

Tungsten Carbide Silicon Carbide Tungsten Alumina Titanium Carbide Silicon Nitride Nickel CFRP Iron Low alloy steels Stainless steel Mild steel Copper Titanium Silicon Silica glass

14 2.5

17 3.2

450 650 450 410 390 380 320 - 270 215 70 200 196 200 - 210 190 - 200 196 124 116 107 94

0.22 0.22 0.30 0.25 0.19 0.22 0.31 0.20 0.30 0.30 0.30 0.30 0.34 0.30 0.22 0.16

13.4 3.9 4.9 3.2 8.9 1.5-1.6 7.9 7.8 7.5-7.7 7.8 8.9 4.5 2.5-3.2 2.6

Aluminum & alloys Concrete

2.6-2.9 2.4-2.5

69-79 45-50

0.35 0.3

GFRP Wood, parallel grain Polyimides Nylon PMMA Polycarbonate Natural Rubbers

1.4-2.2 0.4-0.8 1.4 1.1 1.2 1.2 1.3 1.2

7-45 9-16 3-5 2 3.4 2.6 0.01-0.1 4 0.2 0.1-0.45 0.25 0.35-0.4 0.36 0.49

0.83-0.91

PVC

1.3-1.6

0.003-0.01

0.41

3.2.5 Other Elastic Constants

bulk, shear and Lame modulus.

Youngs modulus and Poissons ratio are the most common properties used to characterize elastic solids, but other measures are also used. For example, we define the shear modulus, bulk modulus and Lame modulus of an elastic solid as follows:

A nice table relating all the possible combinations of moduli to all other possible combinations is given below. Enjoy!

LAME MODULUS

SHEAR MODULUS

YOUNGS MODULUS

POISSONS RATIO

BULK MODULUS

Irrational

Irrational

Irrational

3.2.6 Physical Interpretation of elastic constants for isotropic solids It is important to have a feel for the physical significance of the two elastic constants E and . Youngs modulus E is the slope of the stress dimensions of stress ( strain curve in uniaxial tension. It has ) and is usually large for

steel, . You can think of E as a measure of the stiffness of the solid. The larger the value of E, the stiffer the solid. For a stable material, E>0.

is the ratio of lateral to longitudinal strain in uniaxial tensile stress. It is dimensionless and typically ranges from 0.2 0.49, and is around 0.3 for most metals. For a stable material, . It is a measure of the compressibility of the solid. If , the solid is incompressible its volume remains constant, no matter how it is deformed. If , then stretching a specimen causes no lateral contraction. Some bizarre materials have -- if you stretch a round bar of such a material, the bar increases in diameter!!
Poissons ratio Thermal expansion coefficient quantifies the change in volume of a material if it is heated in the absence of stress. It has dimensions of (degrees Kelvin) and is usually very
-1

small.

For

steel,

The bulk modulus quantifies the resistance of the solid to volume changes. It has a large value (usually bigger thanE). The shear modulus quantifies its resistance to volume preserving shear deformations. Its value is usually somewhat smaller than E.

3.2.7 Strain Energy Density for Isotropic Solids Note the following observations If you deform a block of material, you do work on it (or, in some cases, it may do work on you) In an elastic material, the work done during loading is stored as recoverable strain energy in the solid. If you unload the material, the specimen does work on you, and when it reaches its initial configuration you come out even. The work done to deform a specimen depends only on the state of strain at the end of the test. It is independent of the history of loading. Based on these observations, we define the strain energy density of a solid as the work done per unit volume to deform a material from a stress free reference state to a loaded state. To write down an expression for the strain energy density, it is convenient to separate the strain into two parts where, for an isotropic solid, represents the strain due to thermal expansion (known as thermal strain), and

is the strain due to mechanical loading (known as elastic strain). Work is done on the specimen only during mechanical loading. It is straightforward to show that the strain energy density is

You can also re-write this as

Observe that

3.2.8 Stress-strain relation for a general anisotropic linear elastic material stiffness and compliance tensors

the elastic

The simple isotropic model described in the preceding section is unable to describe the response of some materials accurately, even though the material may deform elastically. This is because some materials do have a characteristic orientation. For example, in a block of wood, the grain is oriented in a particular direction in the specimen. The block will be stiffer if it is loaded parallel to the grain than if it is loaded perpendicular to the grain. The same observation applies to fiber reinforced composite materials. Generally, single crystal specimens of a material will also be anisotropic this is important when modeling stress effects in small structures such as microelectronic circuits. Even polycrystalline metals may be anisotropic, because a preferred texture may form in the specimen during manufacture. A more general stress strain relation is needed to describe anisotropic solids. strain relation has the form

The most general linear stress

Here,

is a fourth order tensor (horrors!), known as the elastic stiffness tensor, is the thermal expansion coefficient tensor. The stress

and strain relation is invertible:

where

is known as the elastic compliance tensor

At first sight it appears that the stiffness tensor has 81 components. Imagine having to measure and keep track of 81 material properties! Fortunately, following symmetries must have the

This reduces the number of material constants to 21. The compliance tensor has the same symmetries as . , note that

To see the origin of the symmetries of

The stress tensor is symmetric, which is only possible if If a strain energy density exists for the material, the elastic stiffness tensor must satisfy The previous two symmetries imply since . To see that , note that by definition and ,

and recall further that the stress is the derivative of the strain energy density with respect to strain

Combining these,

Now, note that

so that These symmetries allow us to write the stress-strain relations in a more compact matrix form as

where , etc are the elastic stiffnesses of the material. The inverse has the form

where etc are the elastic compliances of the material.

To satisfy Drucker stability, the eigenvalues of the elastic stiffness and compliance matrices must all be greater than zero. HEALTH WARNING: The shear strain and shear stress components are not always listed in the order given when defining the elastic and compliance matrices. The conventions used here are common and are particularly convenient in analytical calculations involving anisotropic solids. But many sources use other conventions. Be careful to enter material data in the correct order when specifying properties for anisotropic solids.

3.2.9 Physical Interpretation of the Anisotropic Elastic Constants. It is easiest to interpret , rather than . Imagine applying a uniaxial stress, say , to an anisotropic specimen. In general, this would induce both extensional and shear deformation in the solid, as shown in the figure. The strain induced by the uniaxial stress would be

All the constants have dimensions a uniaxial compliance, (like

. The constant ), while the ratios

looks like

are generalized versions of Poissons ratio: they quantify the lateral contraction of a uniaxial tensile specimen. The shear terms are new in an isotropic material, no shear strain is induced by uniaxial tension. 3.2.10 Strain energy density for anisotropic, linear elastic solids The strain energy density of an anisotropic material is

3.2.11 Basis change formulas for anisotropic elastic constants The material constants or for a particular material are usually specified in a basis with coordinate axes aligned with particular symmetry planes (if any) in the material. When solving problems involving anisotropic materials it is frequently necessary to transform these values to a coordinate system that is oriented in some convenient way relative to the boundaries of the solid. Since tedious, unfortunately. is a fourth rank tensor, the basis change formulas are highly

Suppose that the components of the stiffness tensor are given in a basis , basis, tensor form with components and we wish to determine its components in a second

. We define the usual transformation , or in matrix

This

is

an

orthogonal

matrix

satisfying

. In practice, the matrix can be computed in terms of the angles between the basis vectors. It is straightforward to show that stress, strain, thermal expansion and elasticity tensors transform as

The basis change formula for the elasticity tensor in matrix form can be expressed as where the basis change matrix K is computed as

and the modulo function satisfies

Although these expressions look cumbersome they are quite convenient for computer implementation. The basis change for the compliance tensor follows as where

The proof of these expressions is merely tiresome algebra and will not be given here. Tings book `Anisotropic Elasticity: Theory and Applications OUP (1996) has a nice clear discussion. For the particular case of rotation through an angle the in a counterclockwise sense about

axes, respectively, the rotation matrix reduces to

where

The

inverse matrix can be obtained simply by changing the sign of the angle in each rotation matrix. Clearly, applying the three rotations successively can produce an arbitrary orientation change. For an isotropic material, the elastic stress-strain relations, the elasticity matrices and thermal expansion coefficient are unaffected by basis changes.

3.2.12 The effect of material symmetry on stress-strain relations for anisotropic materials A general anisotropic solid has 21 independent elastic constants. Note that in general, tensile stress may induce shear strain, and shear stress may cause extension. If a material has a symmetry plane, then applying stress normal or parallel to this plane induces only extension in direction normal and parallel to the plane For example, suppose the material contains a single symmetry plane, and let to this plane. Then matrix ( the components of the elastic be normal stiffnes

). (symmetrical terms also vanish, of course). This leaves 13 independent constants. Similar restrictions on the thermal expansion coefficient can be determined using symmetry conditions. Details are left as an exercise. In the following sections, we list the stress-strain relations for anisotropic materials with various numbers of symmetry planes.

3.2.13 Stress-strain relations for linear elastic orthotropic materials An orthotropic material has three mutually perpendicular symmetry planes. This type of material has 9 independent material constants. With basis vectors perpendicular to the symmetry plane, the elastic stiffness matrix has the form

This relationship is sometimes expressed in inverse form, in terms of generalized Youngs moduli and Poissons ratios (which have the same significance as Youngs modulus and Poissons ratio for uniaxial loading along the three basis vectors) as follows

Here the generalized Poissons ratios are not symmetric but instead satisfy that the stiffness matrix is symmetric. (no sums). This ensures

The engineering constants are related to the components of the compliance tensor by

or in inverse form

For an orthotropic material thermal expansion cannot induce shear (in this basis) but the expansion in the three directions need not be equal. Consequently the thermal expansion coefficient tensor has the form

3.2.14 Stress-strain relations for linear elastic Transversely Isotropic Material A special case of an orthotropic solid is one that contains a plane of isotropy (this implies that the solid can be rotated with respect to the loading direction about one axis without

measurable effect on the solids response). Choose plane. Then, transverse isotropy requires that , ,

perpendicular to this symmetry ,

, so that the stiffness matrix has the form

The engineering constants must satisfy

and the compliance matrix has the form

where Poissons ratios are not symmetric, but satisfy

. As before the

The engineering constants and stiffnesses are related by

For this material the two thermal expansion coefficients in the symmetry plane must be equal, so the thermal expansion coefficient tensor has the form

3.2.15 Representative values for elastic constants of transversely isotropic hexagonal close packed crystals Hexagonal close-packed crystals are an example of transversely isotropic materials. The axis must be taken to be perpendicular to the basal (0001) plane of the crystal, as shown in the picture. Since the plane perpendicular to the orientation of and is arbitrary. is isotropic

A table of values of stiffnesses (taken from Freund and Suresh, Thin Film Materials, CUP 2003) is listed below. F&S list the original sources for their data on page 163.

(GPa)
Be C 292.3 1160

(GPa)
336.4 46.6

(GPa) (GPa)
162.5 2.3 26.7 290

(GPa)
14 109

Cd Co Hf Mg Ti Zn Zr ZnO

115.8 307 181.1 59.7 162.4 161 143.4 209.7

51.4 358.1 196.9 61.7 180.7 61 164.8 210.9

20.4 78.3 55.7 16.4 46.7 38.3 32 42.5

39.8 165 77.2 26.2 92 34.2 72.8 121.1

40.6 103 66.1 21.7 69 50.1 65.3 105.1

The engineering constants can be calculated to be

( (GPa)
Be C Cd Co Hf Mg Ti Zn Zr ZnO 289.38 903.69 83.02 211.30 139.87 45.45 104.37 119.45 98.79 127.30

GPa)
335.17 30.21 30.21 313.15 163.07 50.74 143.27 35.28 125.35 144.12 0.09 0.04 0.09 0.49 0.35 0.36 0.48 -0.06 0.40 0.44 0.04 0.08 0.26 0.22 0.26 0.25 0.27 0.26 0.30 0.32 0.04 2.25 0.72 0.15 0.22 0.23 0.20 0.87 0.24 0.28

(GPa)
162.50 2.30 20.40 78.30 55.70 16.40 46.70 38.30 32.00 42.50

(GPa) 132.80 435.00 38.00 71.00 51.95 16.75 35.20 63.40 35.30 44.30

3.2.16 Linear elastic stress-strain relations for cubic materials A huge number of materials have cubic symmetry all the FCC and BCC metals, for example. The constitutive law for such a material is particularly simple, and can be parameterized by only 3 material constants. Pick basis vectors perpendicular to the symmetry planes, as shown. Then

or in terms of engineering constants

This is virtually identical to the constitutive law for an isotropic solid, except that the shear modulus is not related to the Poissons ratio and Youngs modulus through the usual relation given in Section 3.1.6. In fact, the ratio

provides a convenient measure of anisotropy. For

the material is isotropic.

For this material the thermal expansion coefficient matrix must be isotropic. The relationships between the elastic constants are

3.2.17 Representative values for elastic properties of cubic crystals and compounds A table of elastic constants for various cubic crystals and compounds (modified from Simmons and Wang Single Crystal Elastic Constants and Calculated Aggregate Properties MIT Press (1970)) is given below Material Ag Al Au Cu Ir Ni Pb Pd Pt Cr Fe K Li Mo Na Nb Ta V W (fcc) (fcc) (fcc) (fcc) (fcc) (fcc) (fcc) (fcc) (fcc) (bcc) (bcc) (bcc) (bcc) (bcc) (bcc) (bcc) (bcc) (bcc) (bcc)

(G (GPa)
124.00 107.30 192.90 168.40 580.00 246.50 49.50 227.10 346.70 339.80 231.40 4.14 13.50 440.80 6.15 240.20 260.20 228.00 522.40

(GPa) (GPa)
46.10 28.30 41.50 75.40 256.00 127.40 14.90 71.70 76.50 99.00 116.40 2.63 8.78 121.70 5.92 28.20 82.60 42.60 160.80 93.40 60.90 163.80 121.40 242.00 147.30 42.30 176.00 250.70 58.60 134.70 2.21 11.44 172.40 4.96 125.60 154.50 118.70 204.40

Pa)
43.75 63.20 42.46 66.69 437.51 136.31 10.52 73.41 136.29 322.56 132.28 2.60 3.00 343.86 1.72 153.95 145.08 146.72 407.43 0.43 0.36 0.46 0.42 0.29 0.37 0.46 0.44 0.42 0.15 0.37 0.35 0.46 0.28 0.45 0.34 0.37 0.34 0.28

(GP a)
46.10 28.30 41.50 75.40 256.00 127.40 14.90 71.70 76.50 99.00 116.40 2.63 8.78 121.70 5.92 28.20 82.60 42.60 160.80 3.01 1.22 2.85 3.21 1.51 2.57 4.14 2.81 1.59 0.70 2.41 2.73 8.52 0.91 9.95 0.49 1.56 0.78 1.01

C Ge Si GaAs GaP InP KCl LiF MgO NaCl TiC

(dc) (dc) (dc)

949.00 128.40 166.20 118.80 141.20 102.20 39.50 114.00 287.60 49.60 500.00

521.00 66.70 79.80 59.40 70.50 46.00 6.30 63.60 151.40 12.90 175.00

151.00 48.20 64.40 53.70 62.50 57.60 4.90 47.70 87.40 12.40 113.00

907.54 102.09 130.23 85.37 102.85 60.68 38.42 85.86 246.86 44.64 458.34

0.14 0.27 0.28 0.31 0.31 0.36 0.11 0.29 0.23 0.20 0.18

521.00 66.70 79.80 59.40 70.50 46.00 6.30 63.60 151.40 12.90 175.00

1.31 1.66 1.57 1.82 1.79 2.06 0.36 1.92 1.51 0.69 0.90