3

FIRDAUS BIN MAHAMAD | UNIVERSITI TEKNOLOGI MALAYSIA

2 LITERATURE REVIEW
2.1 Characteristics of Quasi-Continuous Method
Detailed description of QCM was already made by Lan for planar wigs. However, for
convenience, a brief explanation of the essential feature of QCM is repeated here. One of the
characteristics of QCM is in the treatment of the continuous loading in chordwise direction.
Since the spanwise loading distribution is assumed stepwise constant, we may explain at first the
numerical procedure of the chordwise integration by the case of two-dimensional wing. The
downwash integral is expressed as follow,
() =
1
2n
_
y(
i
)

i
J
i
1
0
. (1)
where () is vortex strength and is non-dimensional chordwise coordinate. Transforming the
-coordinate into -coordinate through the relation
=
1
2
(1 cos o) . . . . . . (2)
Eq. (1) can be written as
(o) =
1
2n
_
y(o
i
) sin o
i
cos o cos o
i
Jo
i
. . (S)
n
0

Denoting further
g(o) = y(o) sin o . . (4)
and eliminating the Cauchy singularity in the integrand, Eq. (3) is rewritten as
(o) =
1
2n
_
g(o
i
) g(o)
cos o cos o
i
n
0
Jo
i

g(o)
2n
_
Jo
i
cos o cos o
i
n
0

=
1
2n
_
g(o
i
) g(o)
cos o cos o
i
n
0
Jo
i
, . . (S)
4


FIRDAUS BIN MAHAMAD | UNIVERSITI TEKNOLOGI MALAYSIA
Since g() does not contain square root singularity at leading edge, the integrand in Eq. (5) is
infinite everywhere. Thus the integral can be reduced to a finite sum through midpoint
trapezoidal rule as follows.
(o)
1
2N

g(o
u
) g(o)
cos o cos o
u
N
u=1

=
1
2N

g(o
u
)
cos o cos o
u
N
u=1
+
g(o)
2N

1
cos o cos o
u
N
u=1
. . (6)
where
N = number of chordwise integration points,
o
u
=
(2
u
1)
2N
n, (u = 1, 2, , N) . . (7)
Control points, where flow tangency condition is to satisfied, are chosen so as to
eliminate the second term of Eq. (6) by using a characteristic of Chebychev polynomials as

1
cos o
]
cos o
u
N
u=1
= u . . (8)
where
o
]
=
]
N
n, (] = 1, 2, , N), . . . . (9)
Then the following equation is obtained
(o
]
) =
1
2N

g(o
u
)
cos o
]
coso
u
=
1
2N

y(o
u
) sin o
u
cos o
]
cos o
u
N
u=1
N
u=1
(1u)
As shown in the above, chordwise vortex distribution is treated as continuous in QCM,
but the resulting numerical formula Eq. (10) looks like that of VLM in which discrete and
5


FIRDAUS BIN MAHAMAD | UNIVERSITI TEKNOLOGI MALAYSIA
concentrated vortex distribution is used. In case of two-dimensional wing, vortex distribution
() obtained by QCM agree very well with analytical solution.
As for three-dimensional wing, the characteristics of QCM can be summarized as
follows;
1) Continuous vortex distribution over a wing is replaced with a quasi-continuous one, i.e.
continuous in chordwise direction and stepwise constant in spanwise direction. In the
surface integral over a chordwise vortex strip, spanwise integration is carried out
analytically, while chordwise integration is carried out numerically by the midpoint
trapezoidal rule. The square root singularity at leading edge and the Cauchy singularity
are properly accounted for as mention above.

2) Loading points (integration points) and control points over a wing are arranged according
to the semi-circle method as shown in Fig. 1. Chordwise arrangement is chosen so as to
eliminate the Cauchy singularity. Since control points are placed on trailing edge, Kutta
condition can be satisfied automatically, i.e. the flow is tangent to wing at the trailing
edge. In the spanwise direction, finer vortex strips are used toward wing tip where
sectional properties vary rapidly. Outermost loading sections do not coincide with wing
tips and it contributes to the quick convergence of calculation.

Fig. 1 Arrangement of loading and control points over a wing
6


FIRDAUS BIN MAHAMAD | UNIVERSITI TEKNOLOGI MALAYSIA
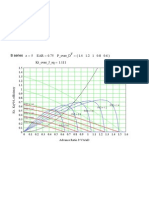
3) Accuracy in circulation is satisfactory. As an example, the results calculated for a planar
circular wing are shown in comparison with analytical solution in Fig. 2. Spanwise lift
distribution and chordwise loading distributions at center (=0.0) and at quarter-span
(=0.50) sections obtained by QCM agree very well with analytical solution. Sufficient
accuracy is retained also in the neighborhood of wing tip (=0.98). Geometry of the
propeller blade in tip region is similar to that of the circular wing. Then accurate solution
can be expected in the neighborhood of the propeller blade tip.
4) Quick convergence is attained. Fig. 3 shows the result calculated for a planar rectangular
wing of aspect ratio 2.0. The numbers of spanwise control points M and chordwise
control points N were varied systematically. Converged solution is obtained with a small
number of control points.



Fig. 2 Spanwise lift and chordwise loading distributions for a planar circular wing
7


FIRDAUS BIN MAHAMAD | UNIVERSITI TEKNOLOGI MALAYSIA

Fig. 3 Lift coefficient for a planar rectangular wing of aspect ratio 2.0

2.2 Formulation of Numerical Model of Propeller Lifting Surface
Propeller blades are represented by the distributions of vortices and sources on the mean
camber surface of blades together with the associated distribution of vortices shed into the wake.
The vortex system, i.e. the distribution of horseshoe vortices which consist of bound vortices and
free vortices shed from both edges of bound vortices, represents blade loading and wake, and the
source distribution represents blade thickness.
Continuous distributions of bound vortices and sources are replaced with quasi-
continuous ones according to QCM. Thus the blades are covered with a number or vortex strips
with associated free vortices and source strips.
Loading points and control points are arranged on the mean chamber surface of blade
according to QCM. In the radial direction, loading stations (radial coordinates of the edges of
each vortex/ source strip) and control stations (radial coordinates of control points) are chosen at
the radii defined as follows. For loading stations
r
L
=
1
2
(r
0
+ r
B
)
1
2
(r
0
r
b
) cos [

,
p = 1, 2, , H+1

8


FIRDAUS BIN MAHAMAD | UNIVERSITI TEKNOLOGI MALAYSIA
and for control stations
r
c
=
1
2
(r
0
+ r
B
)
1
2
(r
0
r
b
) cos [

,
i = 1, 2, , H,
where
ro = propeller radius,
rB = boss radius,
M = number of radial control points,
[

=
2p 1
2(H+1)
n, (p = 1, 2, , H+ 1)
[

=
i
H+1
n, (i = 1, 2, , H+1)
At the loading and control stations, chordwise loading and control points are arranged according
to QCM, i.e. for loading points
s
v
= s
L
(r
L
) +
1
2
c(r
L
)(1 cos o
v
),

v = 1, 2, , N,
and for control points
s
]
= s
L
(r
c
) +
1
2
c(r
c
)(1 cos o
]
),
] = 1, 2, , N,
where
N = number of chordwise control points,
o
v
=
(2v 1)
2N
n, (v = 1, 2, , N),
o
]
=
]
N
n, (] = 1, 2, , N),

9


FIRDAUS BIN MAHAMAD | UNIVERSITI TEKNOLOGI MALAYSIA
Then, loading points and control points are arranged on the same fraction-chord lines
respectively. An example of arrangement of loading lines and loading stations with control
points is shown in Fig. 4. Free vortices are shed only from the loading stations due to stepwise
distribution of vortices. The trailing vortex sheet (free vortex sheet in the wake) is, therefore
composed of (M+1) helical vortices.








Fig. 4 Arrangement of loading lines, and
loading stations and control points

Fig. 5 Vortex segment and horseshoe
vortex
2.3 Calculation of Induced Velocities
Induced velocity at a control point Pij due to a vortex segment of unit strength place
between loading point Q and Q + 1 is given by Biot-Savart law as
u
]v
v
=
1
4n

r
1
r
12

|r
1
r
12
|
2
_
r
2

|r
2
|

r
1

|r
1
|
_ . r
12
. (11)



10


FIRDAUS BIN MAHAMAD | UNIVERSITI TEKNOLOGI MALAYSIA
Consider a horseshoe vortex of unit strength, which consists of bound vortex placed at
Q and Q + 1 and two free vortices shed from Q and Q + 1 in the chordwise direction along
loading stations (see Fig.5). Induced velocity at a control point Pij due to this horseshoe vortex is
expressed by
u
]v
u
= u
]v
B
+ [u
]+1v
|
P
u
]v
|
P
+ u
]+1
1
u
]
1
N
v
|
= v

where
u
]v
B
= induced velocity at Pij due to vortex segment (bound vortex) of unit strength
placed between Q and Q +1,
u
]v
P
= induced velocity at Pij due to vortex segment (free vortex) of unit strength
placed between Q and Q +1,
u
]
1
= induced velocity at Pij due to trailing vortex of unit strength shed from
trailing edge at loading station r = rL,
u
]v
B
and u
]v
P
can be calculated by Eq.11 and u
]
1
also can be calculated with Eq. 11 by
replacing helical vortex line with vortex segments of appropriate length.
Let the strength of bound vortices in the - th vortex strip be (s), then induced velocity
at Pij due to horseshoe vortices on the vortex strip is expressed based on the procedure described
in the previous section, as
I

]
u
= _ y

s1
sL
(s
i
)u
]
u
(s
i
)Js
i

=
c

2
_ y

n
0
(o
i
)u
]
u
(o
i
) sin o
i
Jo
i


nc

2N
y

N
v=1
(o
v
)u
]
u
(o
v
) sin o
v

11


FIRDAUS BIN MAHAMAD | UNIVERSITI TEKNOLOGI MALAYSIA
=
nc

2N
y
v
N
v=1
u
]v
u
sin o
v
,
where
c

= c(y
c
), y
v
= y

(o
v
), u
]v
u
= u
]
u
(o
v
).
The induces velocity a control point Pij due to whole vortex system is obtained by the next
equation
I

]
u
= I

]k
u
M
=1
K
k=1

=
n
2N
c

M
=1
K
k=1
y
v
N
v=1
u
]vk
u
sin o
v
,
where the suffix k shows the contribution from the k-th blade.
Next, consider the induced velocity due to the source distribution. Induced velocity at a
control point Pij due to a source segment of unit strength placed between loading point Q and
Q + 1 (see Fig. 5) is given in a similar manner to that of vortex segment by
u
]v
s
=
1
4n

r
1
r
12

|r
1
r
12
|
2
_
r
2

|r
2
|

r
1

|r
1
|
_ . |r
12
|.
Denoting the source strength at the -th loading point in the -th source strip by , the induced
velocity at a control point Pij due to whole source distribution is expressed as
I

]
s
=
n
2N
c

M
=1
K
k=1
o
v
N
v=1
u
]vk
s
sin o.
2.4 Calculation of Thrust, Torque and Pressure Distribution
2.4.1 Potential Component
Force acting on a vortex/source segment placed between Q and Q+1 can be obtained from
Kutta-Joukowski theorem and Lagallys therorm as
F

v
= p I

v
y
v
p I

v
o
v
|t
v
|
12


FIRDAUS BIN MAHAMAD | UNIVERSITI TEKNOLOGI MALAYSIA
where
I

v
= I

v
u
+ I

v
s
+ I

v
I

= resultant flow velocity at the midpoint of segment
y
v
= y
v
t
v

= vortex segment vector
t
v
= segment vector
v

+1v

= fluid density
Then, thrust and torque acting on whole propeller are obtained by following equations,
I
0
= K_ Jr
i

B
_ F
x
s
T
s
L
Js
i

= K
nc

2N
M
=1
(F
x
)
v
N
v=1
sin o
v
,

0
= K_ Jr
i

B
_ (F

. z + F
z
. y)Js
i
s
T
s
L

= K
nc

2N
M
=1
j(F

)
v
z
v
+(F
z
)
v
y
v
[
N
v=1
sin o
v
,
where
(Fx), (Fy), (Fz)=x-, y- and z- components of F

v
, x, y, z = x-, y- and z- coordinate at the
midpoint of the segment, c

= cord length at r= (rL + rL+ 1).

In addition to the forces acting on vortex and source distributions mentioned in the above,
leading edge suction force must be taken into consideration. The leading edge suction force
results from leading edge singularity of vortex distribution under thin wing assumption. The
suction force per unit span is given by
F
s
=
1
4
npcC
s
2

13


FIRDAUS BIN MAHAMAD | UNIVERSITI TEKNOLOGI MALAYSIA
where
C
s
= lim
ssL
y(s)_
s s
L
c

and the coefficient Cs can be obtained directly in QCM then, trust and torque resulting from
leading edge suction force are expressed as
I
s
= K_ F
s
(r
i
) sin (

B
r
i
)Jr
i

= K
n(r
0
r
B
)
2H
F
s
(r
c
) sin (r
c
) sin [

M
=1


s
= K_ F
s
(r
i
) cos (

B
r
i
)r
i
Jr
i

= K
n(r
0
r
B
)
2H
F
s
(r
c
) cos (r
c
) r
c
sin [

M
=1

2.4.2 Viscous Component
Let the viscous drag coefficient of blade element at the radius r be CD (r) , then trust and torque
due to viscous drag are expressed as
I

= K
1
2
p _ C

(r
i
)w

B
(r
i
)I

x
(r
i
)c(r
i
)Jr
i

= Kp
n(r
0
r
B
)
4H
C

(r
c
) w

(r
c
). I

x
M
=1
(r
c
)c(r
c
) sin [

= K
1
2
p _ C

(r
i
)w

B
(r
i
)I

0
(r
i
)c(r
i
)r
i
Jr
i

= Kp
n(r
0
r
B
)
4H
C

(r
c
) w

(r
c
). I

0
M
=1
(r
c
)c(r
c
) sin [

14


FIRDAUS BIN MAHAMAD | UNIVERSITI TEKNOLOGI MALAYSIA
where
w

(r) = I

x
(r)
2
+ I

0
(r)
2
,
I

x
(r) = x-component of resultant flow velocity averaged in the chorwise direction.
I

0
(r) = -component of resultant flow velocity averaged in the chordwise direction.
The total thrust and torque are given by
T= T0+Ts+TD,
Q= Q0+Qs+QD,
The trust coefficient KT, torque coefficient KQ and propeller efficiency eP are defined by
K
1
=
1
pn
2

4
, K

pn
2

S
, cp =
]
2n
.
K
T
K
Q

where
D = propeller diameter,
n = propeller revolutions per unit time,
J = VA/nD : advance distribution
The result flow velocities on back and face at the control points Pij on the mean camber surface
are surface are expressed as
I

]_
= I

]
u
+I

]
S
+I

]
I
_
1
2
(y
]
.
]
+ o
]
. n
]
),
where
ij = vortex strength at Pij,
ij = source strength at Pij,

]
= unit chordwise tangent vector at Pij.




15


FIRDAUS BIN MAHAMAD | UNIVERSITI TEKNOLOGI MALAYSIA
Subscripts denote back (suction side) and face (pressure side) respectively. The pressure
coefficients at point Pij on back and face are expressed by Bernoullis theorem as
C
]_
=

]_

0
1
2
pw
0
2

= 1
|I

]_
|
2
w
0
2
,
where
P0 = ambient pressure in uniform flow,
W0 = I

2
+(r
c
)
2
.