Professional Documents
Culture Documents
HOW IS THE WEB LIKE A SNOWFLAKE ? by David Matthews
Uploaded by
Leslie CarrCopyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
HOW IS THE WEB LIKE A SNOWFLAKE ? by David Matthews
Uploaded by
Leslie CarrCopyright:
Available Formats
H OW IS THE W EB LIKE A SNOWFLAKE ?
D.Matthews dm1x07@soton.ac.uk Supervisors: Dr. J. Anderson, Dr. R. Carare Fractals
In the late 1600s Leibnitz studied structures that appear the same when we view them (or an appropriate substructure) at different length scales. An example from nature of such a structure is the fern which we would nd it difcult to distinguish from a magnied fern leaf or an extremely magnied fern leafs smaller leaf. Surprisingly it was not until the 1960s and arguably the development of computers that Benoit Mandelbrot coined the word "fractal" for these types of object and thrust fractals rmly into the public imagination. In mathematics models of random processes and geometry are fertile sources of fractals, Figure 1 below shows the Mandelbrot set which is a fractal arising from pure mathematics. Two reason that fractals became popular in the academic and wider world are: (i) They occur naturally, for example fern leaves and snowakes are very nearly fractals. (ii) They are beautiful and have inspired artists such as Jackson Pollock.
Properties of Graphs
We have seen that graphs or networks are built from nodes and edges and can be associated with a vast array of natural, social and technical phenomena. Remarkably this array includes examples as diverse as the Web, the cerebral arterial tree and the metabolism of E. Coli. What is even more astonishing is that all these networks, along with countless others exhibit the following two properties: (i) the small-world property Given a pair of nodes in the network there exists a path along edges and nodes which is incredibly short relative to the size of the network as a whole. (ii) scale free behaviour If we plot the degree of a node against the number of nodes with that degree we get a decreasing power law. We should note that scale free does not necessarily mean that we can consider these networks fractal but there is a close correspondence.
Current Research
In order to answer the question, "to what extent are these networks fractal?" we have conducted a survey of biological and technical graphs (particularly trees) with the aim of generating multidisciplinary questions pertaining to the structure of the Web graph and its various subgraphs. We focused our attention on Altzheimers disease since geometric features such as the average degree in the cerebral arterial tree (shown in Figure 2) plays a pivotal role in the progression of this disease. By designing and investigating models of Altzheimers Figure 2: disease we are able to draw parallels between the natural structure of the cerebral vasculature and the structure of an online social network. Murrays law of least work states that a natural process will evolve to minimize its energy loss has been cited as the force that drives the fractal structure of the cerebral vasculature [2]. This naturally begs the questions: what is the extent to which online social networks exhibit fractal properties and are there technological and social equivalents of Murrays law?
Figure 1: The Mandelbrot set
Graphs
Fractal structures also appear naturally in the study of random graphs. Loosely speaking a graph G consists of a set of nodes N and a set of edges E together with a function that assigns the two ends of each edge to a node. We write G = G(N, E). As well as being interesting of themselves graphs have successfully been used to represent a variety of real-world phenomena. For example we can represent the Web as a graph by assigning every webpage to a node and then linking two nodes if the associated webpages are linked. This model is so well established it has been named the Web graph. One way of modelling the Web, particularly the growth of the Web is by building a graph using a random process which adds nodes and edges over time. Representing phenomena like the Web by a graph is useful because properties of the graph such as the degree of each vertex (how many edges subtend a node) represent real world data such as the number of links that a webpage has. Given a graph G, we can construct a new graph by taking any subset, M , of N and all edges in E that have both ends assigned to a node in M . We calls such a graph a subgraph of G. A simplied social network site consisting of a set of webpages associated to people and links between them corresponding to social interaction can be thought of as a subgraph of the Web graph. A graph in which every two nodes are joined by following a unique sequence of edges from end to end is called a tree. Trees are easier to calculate with and the following theorem marries graphs with trees. Theorem 1. Every graph G = G(N1, E1) admits a spanning subgraph T = T (N2, E2) such that T is a tree. By a spanning tree we mean a tree T such that N1 = N2. Further, Goh et al. argue that spanning trees of the Web graph can be thought of as an information kernel of information motorways for the more complicated network they span [1].
Future Work
Confusion about the precise denition of fractal pervades the literature describing biological and technical networks and words such as "selfsimilar" are used without due regard for their mathematical denition. Essential further work includes making this literature more rigorous.
Figure 3: A graph with a spanning tree highlighted in blue
References [1] K.I. Goh, B. Salvi, B. Kahng, and D. Kim. "Skeleton and Fractal Scaling in Complex Networks". Physical Review Letter, 96, 018701, 2006. [2] C.D. Murray. "The Physiological Principle of Minimum Work: I. The Vascular System and the Cost of Blood Volume". Proc. Natl. Acad. Sci. U.S.A., 12(3):207-214, 1926.
You might also like
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryFrom EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryRating: 3.5 out of 5 stars3.5/5 (231)
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)From EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Rating: 4.5 out of 5 stars4.5/5 (121)
- Grit: The Power of Passion and PerseveranceFrom EverandGrit: The Power of Passion and PerseveranceRating: 4 out of 5 stars4/5 (588)
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaFrom EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaRating: 4.5 out of 5 stars4.5/5 (266)
- The Little Book of Hygge: Danish Secrets to Happy LivingFrom EverandThe Little Book of Hygge: Danish Secrets to Happy LivingRating: 3.5 out of 5 stars3.5/5 (399)
- Never Split the Difference: Negotiating As If Your Life Depended On ItFrom EverandNever Split the Difference: Negotiating As If Your Life Depended On ItRating: 4.5 out of 5 stars4.5/5 (838)
- Shoe Dog: A Memoir by the Creator of NikeFrom EverandShoe Dog: A Memoir by the Creator of NikeRating: 4.5 out of 5 stars4.5/5 (537)
- The Emperor of All Maladies: A Biography of CancerFrom EverandThe Emperor of All Maladies: A Biography of CancerRating: 4.5 out of 5 stars4.5/5 (271)
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeFrom EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeRating: 4 out of 5 stars4/5 (5794)
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyFrom EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyRating: 3.5 out of 5 stars3.5/5 (2259)
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersFrom EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersRating: 4.5 out of 5 stars4.5/5 (344)
- Team of Rivals: The Political Genius of Abraham LincolnFrom EverandTeam of Rivals: The Political Genius of Abraham LincolnRating: 4.5 out of 5 stars4.5/5 (234)
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreFrom EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreRating: 4 out of 5 stars4/5 (1090)
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceFrom EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceRating: 4 out of 5 stars4/5 (895)
- Her Body and Other Parties: StoriesFrom EverandHer Body and Other Parties: StoriesRating: 4 out of 5 stars4/5 (821)
- MetaphysicsDocument148 pagesMetaphysicsMonizaBorges100% (3)
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureFrom EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureRating: 4.5 out of 5 stars4.5/5 (474)
- The Book of Alignment (Updated)Document165 pagesThe Book of Alignment (Updated)Max KlostermannNo ratings yet
- The Unwinding: An Inner History of the New AmericaFrom EverandThe Unwinding: An Inner History of the New AmericaRating: 4 out of 5 stars4/5 (45)
- Level 3 Health and Social Care PackDocument735 pagesLevel 3 Health and Social Care PackGeorgiana Deaconu100% (4)
- Types of Tests Used in Special EducationDocument5 pagesTypes of Tests Used in Special EducationCbrc CebuNo ratings yet
- The Yellow House: A Memoir (2019 National Book Award Winner)From EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Rating: 4 out of 5 stars4/5 (98)
- Timothy Leary - Space Migration SMIILE PDFDocument53 pagesTimothy Leary - Space Migration SMIILE PDFRichard Woolite100% (1)
- On Fire: The (Burning) Case for a Green New DealFrom EverandOn Fire: The (Burning) Case for a Green New DealRating: 4 out of 5 stars4/5 (73)
- Plato's Theory of ImitationDocument2 pagesPlato's Theory of ImitationAnkitRoy82% (17)
- Chaining and Knighting TechniquesDocument3 pagesChaining and Knighting TechniquesAnaMaria100% (1)
- Auden's The Age of Anxiety in A Jungian and Spiritual ContextDocument18 pagesAuden's The Age of Anxiety in A Jungian and Spiritual ContextBdod6No ratings yet
- Haves Without Have-Nots - Mortimer J. AdlerDocument377 pagesHaves Without Have-Nots - Mortimer J. AdlerA100% (1)
- Plato's Sophist Non-Being and The BeardDocument15 pagesPlato's Sophist Non-Being and The BeardPhilip Reynor Jr.No ratings yet
- Jalal Al-Din Rumi, Maulana, 1207-1273 - Shams-I Tabrizi, D. 1246 - Nicholson, Reynold Alleyne, 1868-1945, Ed - Divani Shamsi TabrizDocument132 pagesJalal Al-Din Rumi, Maulana, 1207-1273 - Shams-I Tabrizi, D. 1246 - Nicholson, Reynold Alleyne, 1868-1945, Ed - Divani Shamsi Tabrizalex_neumann_15No ratings yet
- The Problem of EvilDocument13 pagesThe Problem of Evilroyski100% (2)
- 2) - William Grabe PDFDocument11 pages2) - William Grabe PDFJalal Zbirat67% (3)
- Organizational Development InterventionsDocument57 pagesOrganizational Development InterventionsAmr YousefNo ratings yet
- Format of Debate: Position Paper Four Reason Why Rizal RetractedDocument3 pagesFormat of Debate: Position Paper Four Reason Why Rizal RetractedBrianPlayz100% (1)
- Lesson Exemplar in English 6Document4 pagesLesson Exemplar in English 6Vicmyla Mae A. Cabonelas50% (2)
- Web Science DTC Industry Forum: Opportunities and Challenges 2013Document18 pagesWeb Science DTC Industry Forum: Opportunities and Challenges 2013Leslie CarrNo ratings yet
- Online Collaborative Learning For Mathematics Education by Mandy LoDocument1 pageOnline Collaborative Learning For Mathematics Education by Mandy LoLeslie CarrNo ratings yet
- Is The Web Corrupting The Values of Our Youth? by Huw DaviesDocument1 pageIs The Web Corrupting The Values of Our Youth? by Huw DaviesLeslie CarrNo ratings yet
- The Virtual Body: Video Game Avatars As Self, Cipher, and Sex Object by Elzabi RimingtonDocument1 pageThe Virtual Body: Video Game Avatars As Self, Cipher, and Sex Object by Elzabi RimingtonLeslie CarrNo ratings yet
- Use of Mobile Technology To Support Dyslexic Learning in Higher Education by Katie SpiresDocument1 pageUse of Mobile Technology To Support Dyslexic Learning in Higher Education by Katie SpiresLeslie CarrNo ratings yet
- Classifying Policing Social Machines by Maire Byrne-EvansDocument1 pageClassifying Policing Social Machines by Maire Byrne-EvansLeslie CarrNo ratings yet
- Memory Institutions and The Web - Nicole Beale - University of Southampton Web Science Institute Research Week, Royal Society.Document1 pageMemory Institutions and The Web - Nicole Beale - University of Southampton Web Science Institute Research Week, Royal Society.Nicole BealeNo ratings yet
- Alison Knight Poster Industry Forum 2013 LatestDocument1 pageAlison Knight Poster Industry Forum 2013 LatestLeslie CarrNo ratings yet
- Research Dissemination and Disaggregation by Will FysonDocument1 pageResearch Dissemination and Disaggregation by Will FysonLeslie CarrNo ratings yet
- A Public Health Approach To Cybersecurity by Huw FryerDocument1 pageA Public Health Approach To Cybersecurity by Huw FryerLeslie CarrNo ratings yet
- Enhancing Engagement With Online Museums by Javier PeredaDocument1 pageEnhancing Engagement With Online Museums by Javier PeredaLeslie CarrNo ratings yet
- The Web and Internet Piracy by Keiran RonesDocument1 pageThe Web and Internet Piracy by Keiran RonesLeslie CarrNo ratings yet
- Ontological Representation of Ancient Sumerian Literature Granularity Ontology Structure Formalise CONTENT Express Domain Knowledge Entities Relationships by Terhi NurmikkoDocument1 pageOntological Representation of Ancient Sumerian Literature Granularity Ontology Structure Formalise CONTENT Express Domain Knowledge Entities Relationships by Terhi NurmikkoLeslie CarrNo ratings yet
- The Web & Post-Conflict Governance Building in Fragile States by Jen WelchDocument1 pageThe Web & Post-Conflict Governance Building in Fragile States by Jen WelchLeslie CarrNo ratings yet
- Privacy Choices and Informed Consent by Richard GomerDocument1 pagePrivacy Choices and Informed Consent by Richard GomerLeslie CarrNo ratings yet
- Web Forecasting by Lawrence GreenDocument1 pageWeb Forecasting by Lawrence GreenLeslie CarrNo ratings yet
- Visual Analytics by Paul BoothDocument1 pageVisual Analytics by Paul BoothLeslie CarrNo ratings yet
- The Role of Internet Intermediaries in Enhancing Cybersecurity by Evangelia PapadakiDocument1 pageThe Role of Internet Intermediaries in Enhancing Cybersecurity by Evangelia PapadakiLeslie CarrNo ratings yet
- Towards A Taxonomy For Web Observatories by Ian BrownDocument1 pageTowards A Taxonomy For Web Observatories by Ian BrownLeslie CarrNo ratings yet
- Open Innovation Measurement and Optimisation by Gareth BeestonDocument1 pageOpen Innovation Measurement and Optimisation by Gareth BeestonLeslie CarrNo ratings yet
- Personal Data and Transparency by Reuben BinnsDocument1 pagePersonal Data and Transparency by Reuben BinnsLeslie CarrNo ratings yet
- Predicting Stock Prices With Online Information by Paul GaskellDocument1 pagePredicting Stock Prices With Online Information by Paul GaskellLeslie CarrNo ratings yet
- A Multi-Dimensional Framework of The ICT Innovation System by Chris HughesDocument1 pageA Multi-Dimensional Framework of The ICT Innovation System by Chris HughesLeslie CarrNo ratings yet
- Skim Reading: An Adaptive Strategy For Reading On The Web by Gemma FitszimmonsDocument1 pageSkim Reading: An Adaptive Strategy For Reading On The Web by Gemma FitszimmonsLeslie CarrNo ratings yet
- MOOCS in Higher Education Perspectives From HE Educators by Manual UrrutiaDocument1 pageMOOCS in Higher Education Perspectives From HE Educators by Manual UrrutiaLeslie CarrNo ratings yet
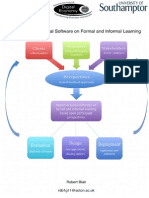
- The Impact of Social Software On Informal and Formal Learning by Robert BlairDocument1 pageThe Impact of Social Software On Informal and Formal Learning by Robert BlairLeslie CarrNo ratings yet
- Web For Environmental Sustainability: Identifying The Emerging Markets of The Cleanweb by Jack TownsendDocument1 pageWeb For Environmental Sustainability: Identifying The Emerging Markets of The Cleanweb by Jack TownsendLeslie CarrNo ratings yet
- Orienting Within Complex Digital Environments Bridging The Gap Between The Inside and Out To Reduce Disorientation by Craig AllisonDocument1 pageOrienting Within Complex Digital Environments Bridging The Gap Between The Inside and Out To Reduce Disorientation by Craig AllisonLeslie CarrNo ratings yet
- Charitable Use of Social Media by Christopher PhetheanDocument1 pageCharitable Use of Social Media by Christopher PhetheanLeslie CarrNo ratings yet
- By Caroline HalcrowDocument1 pageBy Caroline HalcrowLeslie CarrNo ratings yet
- Warnier Jean-Pierr Marching The Devotional Bodily Material K ReligionDocument16 pagesWarnier Jean-Pierr Marching The Devotional Bodily Material K Religioncristian rNo ratings yet
- Critique of "Ali Mirza The Heretic:Refutation of Allegations of Heretic Ali Mirza On Saiyiduna Uthman RD:and His Governors RD:.Document11 pagesCritique of "Ali Mirza The Heretic:Refutation of Allegations of Heretic Ali Mirza On Saiyiduna Uthman RD:and His Governors RD:.AHLUSSUNNAHVSALIMIRZANo ratings yet
- Faulkner Sound and FuryDocument3 pagesFaulkner Sound and FuryRahul Kumar100% (1)
- Succession Under Muslim Law 2Document12 pagesSuccession Under Muslim Law 2Z_JahangeerNo ratings yet
- NGOTips - Fostering Effective NGO GovernanceDocument5 pagesNGOTips - Fostering Effective NGO GovernanceKakak YukaNo ratings yet
- Naess Arne The Shallow and The Deep Long Range Ecology MovementDocument6 pagesNaess Arne The Shallow and The Deep Long Range Ecology MovementGoutam karmakarNo ratings yet
- CrucibleDocument48 pagesCrucibleShaista BielNo ratings yet
- Module 12 - Evaluation TechniquesDocument14 pagesModule 12 - Evaluation TechniqueserikriyaNo ratings yet
- The MountDocument6 pagesThe Mountcrazykate000No ratings yet
- 10.1007/978 3 642 30668 6Document427 pages10.1007/978 3 642 30668 6Atul ChauhanNo ratings yet
- Master of Education (Instructional Technology)Document2 pagesMaster of Education (Instructional Technology)Abel Jason PatrickNo ratings yet
- Grade 1 Syllabus 2019-2020Document15 pagesGrade 1 Syllabus 2019-2020SiiJuliusKhoNo ratings yet
- Boscombe Valley MisteryDocument20 pagesBoscombe Valley Misteryronie1988No ratings yet
- Decalogues and Principles PDFDocument31 pagesDecalogues and Principles PDFهؤلاء الذين يبحثونNo ratings yet