Probability Theory, Math 170b, Winter 2013, Toni Antunovi - Homework 2 c c

From the textbook solve the problems 17, 18, 19, 22, 23 and 24 from the Chapter 4. Solve the problems 21, 22, 24, 30 from the Chapter 4 additional exercises at http://www.athenasc.com/prob-supp.html And also the problems below: Problem 1. Show that for random variables X, Y and Z we have E[E[E[X|Y ]|Z]] = E[X]. Apply this formula to the following problem: Roll a far 6-sided die and observe the number Z that came up. Then toss a fair coin Z times and observe the number of heads Y . Then let X be a number uniformly chosen in the interval [0, Y ]. Find E[X]. Solution: We apply Law of repeated expectation twice to get E[E[E[X|Y ]|Z]] = E[E[X|Y ]] = E[X]. In the example given E[X|Y ] = Y /2, E[E[X|Y ]|Z] = E[Y /2|Z] = Z/4 and E[X] = E[E[E[X|Y ]|Z]] = E[Z/4] = 1 + + 6 5 = . 46 8

Problem 2. A machine prints out the number 1, 2, or 3 with equal probabilities. A machine starts printing numbers independently one after another and stops the rst time it prints 1. Let X denote the number of 2s it printed. Compute E[X] and var(X). Solution: Let Y be the rst time the machine prints 1, so Y is geometric with parameter 1/3 and E[Y ] = 3 and var(Y ) = (1 1/3)/(1/3)2 = 6. Given the value Y we have Y 1 preceding tosses each of which can be either 2 or 3 with equal probabilities. Thus, given Y the random variable X is just binomial with parameters Y 1 and 1/2 and so E[X|Y ] = (Y 1)/2 and var(X|Y ) = (Y 1)/4. Then E[X] = E[E[X|Y ]] = E[(Y 1)/2] = (3 1)/2 = 1 var(X) = E[var(X|Y )] + var(E[X|Y ]) = E[(Y 1)/4] + var((Y 1)/2) = (3 1)/4 + var(Y )/4 = 1/2 + 6/4 = 2.

Problem 3. Break a stick of length 1 at a uniform location and then choose either of the two parts with equal probabilities. If X denotes the length of the part you choose, compute E[X] and var(X). Solution: If Y is the location of the break point, then Y is uniform in the interval [0, 1]. Given Y we either choose Y or 1 Y each with probability 1/2 and so E[X|Y ] = Y /2 + (1 Y )/2 = 1/2,

E[X 2 |Y ] = Y 2 /2 + (1 Y )2 /2 = Y 2 Y + 1/2 and

1

var(X|Y ) = E[X 2 |Y ] (E[X|Y ])2 = Y 2 Y + 1/2 1/4 = Y 2 Y + 1/4.

var(X) = E[var(X|Y )] + var(E[X|Y ]) = E[Y 2 Y + 1/4] + var(1/2) =

0

t2 t + 1/4 dt = 1/12,

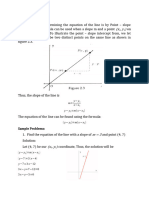
since var(1/2) = 0. Problem 4. Consider the triangle with vertices (0, 0), (1, 0) and (0, 1). Let Z be a uniform random variable in the interval [0, 1]. Draw a vertical line that intersects the x axis at Z. This line divides the triangle in two pieces. Select a point (X, Y ) uniformly at random from the right piece. Find the expectation E[X] of the x coordinate of the selected point. Hint: You might have to integrate an ugly looking function. Factor the numerator, cancel stu and simplify the function. Solution: Given the value of Z the expected x coordinate of chosen point is 2 E[X|Z] = (1 Z)2 Now factor 1/3 Z 2 +
2Z 3 3 1 Z 0 1x

1/3 Z 2 + 2Z 3 x dydx = . (1 Z)2

= (1 Z)2 (1/3 + 2Z/3) and so E[X|Z] = 1/3 + 2Z/3.

Then E[E[X|Z]] = E[1/3 + 2Z/3] = 2/3.