CHAPTER 2.

PRESSURE TRANSIENT ANALYSIS IN DRAWDOWN AND BUILDUP

EPS Training
40

CHAPTER 2. PRESSURE TRANSIENT ANALYSIS IN DRAWDOWN AND BUILDUP......................................39
2.1. Background to Transient Pressure Analysis .........................................................................................41
2.1.1. Introduction .............................................................................................................................41
2.1.2. Development of Pressure Testing .......................................................................................42
2.1.3. Exploration Well Testing........................................................................................................43
2.2. Radial Flow Theory....................................................................................................................................49
2.2.1. The Basic Flow Equations .....................................................................................................49
2.2.2. Fluid of Constant Compressibility........................................................................................50
2.2.3. Further Development of the Accumulation Term...............................................................51
2.2.4. Linearisation of the Radial Flow Equation...........................................................................52
2.2.5. Initial and Boundary Conditions...........................................................................................53
2.2.6. Dimensionless Form of the Diffusivity Equation ...............................................................55
2.2.7. The Line Source Analytical Solution in an Infinite Reservoir..........................................58
2.2.8. Well-bore Damage and Improvement Effects .....................................................................60
2.2.9. Analytical Solution for the Case of a Bounded Circular Reservoir .................................62
2.2.10. Analytical Solution for a Constant Pressure Outer Boundary .......................................65
2.2.11. SPE Field Units ......................................................................................................................66
2.2.12. The Depth of Investigation and Radius of Drainage.......................................................66
2.2.13. The Dynamics of Reservoir Pressure Response..............................................................71
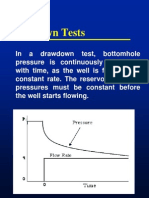
2.3. Pressure Drawdown Testing ....................................................................................................................72
2.3.1. Introduction .............................................................................................................................72
2.3.2. Pressure Drawdown Analysis in Infinite-Acting Reservoirs ...........................................73
2.4. The Principle of Superposition.................................................................................................................76
2.4.1. Introduction .............................................................................................................................76
2.4.2. Multiple-Well Situations........................................................................................................76
2.4.3. Variable Rate Situations .........................................................................................................77
2.5. Pressure Build-Up Testing........................................................................................................................78
2.5.1. Introduction .............................................................................................................................78
2.5.2. Pressure Build-Up Test Analysis during the Infinite-Acting Period ..............................79
2.5.3. After Production......................................................................................................................81
2.5.4. Determination of Reservoir Parameters................................................................................82
2.5.5. Peaceman Probe Radius .........................................................................................................86

EPS Training
41

2.1. Background to Transient Pressure Analysis

2.1.1. Introduction

One of the greatest problems facing the petroleum engineer is that of characterising the physical nature of
the subterranean reservoir from which the crude oil or gas is produced. The significance which can be put on
the results of sophisticated numerical simulations of reservoir performance is entirely dependent on the quality
of reservoir description inherent in the model. The difficulty in obtaining a reliable description stems from the
large scale and heterogeneous nature of the reservoir and the very limited number of points, i.e. wells, at which
observations can be made. In the case of an offshore reservoir this difficulty is compounded by the fact that
the well spacing is much larger than that typical of onshore operation. There are several ways by which it is
possible to gain information about the reservoir characteristics; the most important are:

(a) Seismic and associated geological studies

(b) Information obtained during t he well drilling programme; this comprises:

(1) the analysis of cuttings and cores
(2) the interpretation of various logs

(c) Wireline formation testing

(1) virgin reservoir (exploration and appraisal wells)
(2) produced reservoir (new development wells)

(d) Transient pressure testing of wells (including production logging)

(e) Analysis of reservoir performance, e.g. through history matching a simulator


A consistent description of the reservoir can only be generated by collating and assessing all the available
information from these different sources and synthesising a coherent physical model of the system which
minimises inconsistencies in the data. Note that in the reservoir development stage only items (a), (b) and (c)
are applicable and important engineering decisions will be made on the basis of rather sparse and sometimes
conflicting evidence. It is the subject of transient pressure testing of wells which will be dealt with here.
The pressure behaviour of an oil or gas well is both a readily measurable and a very useful entity. In the
context of pressure testing it is the pressure at the bottom of the well adjacent to the producing formation,
referred to as the bottom-hole pressure (BHP), which is of significance. The pressure analysis of wells
essentially concerns the dynamic relation between the producing rate, the BHP and the reservoir pressure in
the vicinity of the well under consideration. Knowledge of this relation from field tests, combined with a
realistic model for fluid flow in the reservoir rock surrounding the well, allows parameters of the flow system
such as permeability to be established by inference. In fact pressure transient analysis is simply a parameter
estimation technique in which one or more of the parameters of a differential equation are computed from a
measured solution. Parameter estimation is the inverse of simulation and is a well known procedure in systems
engineering. The relation between producing rate, the BHP and the pressure at the well head, referred to as the
top-hole pressure (THP), is known as the vertical lift characteristic of the well and is an entirely separate issue
which is not treated here.
Although the topic is referred to as the pressure testing of wells it is important to appreciate that it is
information about the reservoir which is obtained from such tests. Moreover the information gained is not
restricted in scope to the immediate vicinity of the well-bore as is the case for data from logs. One of the
advantages of transient pressure testing is that it yields average values of permeability taken over substantial
volumes of rock. Since the theory of pressure testing is basically that of unsteady-state, radial flow in the
vicinity of the well bore the reservoir engineering aspects of radial flow will also be covered.


EPS Training
42

2.1.2. Development of Pressure Testing

The technological progress of transient pressure testing is very much linked to the development of sub-
surface measuring instruments for recording bottom-hole pressures. Instruments for measuring maximum
pressures in wells were developed and applied in the United States in the 1920's. However the utility of early
bottom-hole pressure instruments was greatly increased by the development of continuously recording
instruments such as the Amerada gauge; this of course allowed transient pressure changes to be monitored
and laid the foundation for the modern techniques. In the Amerada and similar systems the whole assembly
comprising the pressure element (Bourdon tube), mechanical recording system (based on scribing with a
needle on a tin chart), clock and thermometer are lowered down-hole in a bomb for the period of the test.
Although the Amerada type gauges are still used such mechanical systems have inherent limitations with
regard to accuracy and reproducibility. There is nothing more annoying than to run an expensive pressure test
(in terms of lost oil production or rig time) and then discover, on retrieving the bomb by wireline, that the
internal clock had stopped during the test. However in deep wells, where exceptionally high temperatures are
encountered, the only viable pressure recording instrument may be the purely mechanical Amerada system and
one or two service companies specialise in calibrating gauges and reading Amerada charts with high precision.
The weak link of electronic systems is the batteries used to power the circuitry and memory devices.
There is no doubt that the introduction of the bottom-hole recording system was the spur to the
development of modern, transient well testing as a practical and useful engineering technique. The
measurement of wellhead pressure alone requires that the downhole pressure be deduced using some form of
vertical flow model and there is simply far too much uncertainty in this process. Some success in the testing of
gas wells has been achieved using wellhead pressure measurement only, since in single phase conditions it is
possible to make a much more reliable prediction of the vertical flow characteristics and a commercial device
called the "Spider", which simultaneously measures surface flow-rate and pressure and uses a computer
program to deduce bottomhole pressure, is available. The development of technology which would allow the
accurate measurement of downhole flow-rate, of comparable quality to the extremely accurate detection of
pressure now routinely available, would constitute a further major advance in the subject. At least two service
companies are developing bottom-hole venturi meters, which have the advantage of no moving parts, and may
help to facilitate a good in-situ rate measurement especially in single phase flow. At the present time downhole
flow measurement is limited to the use of conventional production logging tools based on spinner devices and
the accuracy in multiphase conditions is problematic to say the least.
The last two decades have seen a further technological breakthrough with the introduction of very precise
surface recording pressure tools. These were first introduced by the Hewlett-Packard company and are based
on a quartz crystal pressure transducer with accurate temperature compensation; the signal can be transmitted
to the surface where it is displayed and recorded on a digital data logging system. These instruments have
been pioneered in the North Sea and, despite their high cost, have become something of an offshore industry
standard. In deep wells with highly permeable formations it is necessary to accurately measure fairly small
changes in the down-hole pressure at a high pressure level; this demands instrumentation of correspondingly
high sensitivity.
In the early days the usual type of measurement was the determination of the so-called 'static' pressure; this
was done by lowering a pressure-measuring device to the bottom of a well which had been closed-in for a
period of time, say 72 hours. These static measurements sufficed to indicate the pressure in permeable, high-
productivity reservoirs. However petroleum engineers soon recognised that in most formations the static
pressure measurements were very much a function of closed-in time. The lower the permeability, the longer the
time required for the pressure in a well to equalise at the prevailing reservoir pressure. Thus it was realised
very early that the rapidity with which pressure build-up occurred when a well was closed in was a reflection of
the permeability of the reservoir rock around that well. This qualitative observation was an important step in
developing an understanding of well pressure behaviour and led to the other basic type of measurement called
transient pressure testing. In this technique, which is the basis of modern well testing, the pressure variation
with time is recorded after the oil flow-rate of the well is changed.
A stimulus for developing a quantitative interpretation of pressure data came with the introduction of the
material balance method of calculating the original oil in place (OOIP) in a reservoir. This procedure requires
knowledge of the static reservoir pressure and, rather than closing in the wells for long periods of time, the
question naturally arose as to whether flowing transient pressure measurements could be extrapolated in some
way to give a reliable estimate of the pressure that would exist in the reservoir if all fluid motion ceased.
EPS Training
43
The first attempt to present an extrapolation theory and to relate the change in pressure with time to the
parameters of the reservoir was presented in 1937 by Muskat
(1)
. He deduced mathematically a method for
extrapolating the measured well pressure to a true static pressure. At the time Muskat stated that his theory
only had a qualitative application and, in a sense, this was true since the analysis did not take into account the
important aspect of fluid compressibility. However it should be pointed out that in 1935 a French hydrologist,
Charles Theis
(2)
, had presented the theory of pressure buildup analysis now associated with the name of
Horner in the petroleum literature. The first comprehensive treatment of pressure behaviour in oil wells to
include the effects of compressibility was that of Miller, Dyes and Hutchinson
(3)
in 1950. The following year
Horner
(4)
presented a somewhat different treatment. These two papers still furnish the fundamental basis for
the modern theory and analysis of oil well pressure behaviour. Subsequent works have brought a multitude of
refinements and a deeper understanding of the subject. The procedure for extrapolation to static reservoir
pressure was perfected by Matthews, Brons and Hazebroek
(5)
while Ramey
(6)
has extended the theory of
pressure behaviour to cover gas reservoirs. Recent developments have been concerned with the detection of
faults and fractures within the reservoir and with the investigation of the degree of continuity between wells.
This latter aspect is known as interference testing and the state-of-the-art in this area has been radically
improved by the introduction of the new, highly sensitive pressure transducers.
The excellent monograph by Matthews and Russell of Shell Oil entitled 'Pressure Build-up and Flow Tests in
Wells' and published by the SPE in 1967 gives a thorough review of the subject as it stood at that time.

2.1.3. Exploration Well Testing

In broad terms the subject of well testing may be divided into two broad categories, namely, the testing of
exploration or appraisal wells and the testing of development wells. For offshore reservoirs the exploration and
appraisal wells are tested from a semi-submersible rig and the methodology involves down-hole shut-in with
some form of annulus pressure operated testing string as illustrated in Figure 2.1.1. The three principal
elements of the test string are:

- the packer which is usually set by weight on the tail pipe

- the testing valve which is operated by annulus pressure

- the bottom-hole pressure transducer which records the response


1
Muskat, M.:"Use of Data on the Build-Up of Bottom-Hole Pressures",Trans AIME(1937), 123, 44-48
2
Theis, C.V.:"The Relation between the Lowering of the Piezometric Surface and the Rate and Duration
of Discharge of a Well Using Ground Water Storage", Trans AGU (1935), 519-524
3
Miller, C.C, Dyes, A.B. and Hutchinson, C.A.:"The Estimation of Permeability and Reservoir Pressure
from Bottom-Hole Pressure Build-Up Characteristics", Trans AIME (1950), 189, 91-104
4
Horner, D.R.:"Pressure Build-Up in Wells", Third World Petroleum Congress, The Hague (1951), Sec
II, 503-523
5
Matthews, C.S., Brons, F. and Hazebroek,P.:"A Method for Determination of Average Pressure in a
Bounded Reservoir", Trans AIME (1954), 201, 182-191
6
Al-Hussainy, R., Ramey, H.J. and Crawford, P.B.:"The Flow of Real Gases through Porous Media",
JPT (May 1966), 624-636
EPS Training
44
Downhole
Memory
Surface
Recording
Casing
Tubing
Testing Valve
(operated by
annulus pressure)
Packer
(set by weight on
string)
Pressure
Transducer
Tailpipe
Figure 2.1.1
Drillstem
Testing
Assembly
Well Test Surface Hardware
Choke
Gas
Oil
Surface Choke provides
Rate Control
Orifice Plate
Flow Measurement
q
o
Q
Test Rate Limited by
Separator Capacity
Fig 2.1.1b
Test
Separator

A well test conducted with such a system is commonly referred to as a drill stem test (DST) although this
nomenclature is somewhat out of date since in modern practice the test string is not set on drill pipe but on
special tubing. Historically drill stem tests were carried out in open-hole conditions but again in modern
practice the well will have been cased, cemented and perforated before the DST is performed. The important
point about a DST is that the testing valve is downhole and that it is the first test on a new well and hence the
pressure will normally already have been determined by a wireline formation tester (WFT) survey prior to
casing. In the exploration - appraisal well situation the reservoir is unproduced and all layers of the tested
interval are likely to be at the same potential i.e. pressure corrected to datum level. In a typical test the well is
flowed and then shut in by opening and closing the testing valve and the downhole pressure response
recorded by the transducer. The flowrate is normally measured at the surface where the produced fluids are
passed through a separator and the flow-rates of oil, water and gas are individually registered as illustrated in
Figure 2.1.1b. Very recently service companies have introduced a downhole venturi flowmeter which
complements the downhole pressure measurement with downhole flow measurement.
With a modern quartz pressure transducer it is possible to measure pressure to approximately five decimal
places of accuracy. However the rate measurement of the flow-rate of the single-phase fluids from the
separator is not nearly so precise; in fact the error is of the order of t10% which is very disappointing indeed.
Given this poor quality of rate surface measurement it is really only possible to determine permeability within
this error range i.e. t10%. The error in rate measurement also crucially affects the validity of a recombination
sample of the single-phase streams which has been one of the principal sampling techniques. In many
exploration well tests the capacity of the test separator is much lower than the potential flow-rate from the well
in a production system. Therefore the surface choke is used to limit the test rate to a value which can be
handled by the test separator. The oil-field choke in critical (two-phase) flow is not an ideal control device
since the rate still depends on the upstream pressure. A recent innovation is to utilise a muliphase surface
flowmeter and send a feed-back signal to a process engineering pressure control valve (PCV) which will give
much better rate control than a manually variable choke. Test design is based on achieving essentially
constant rate in the flow periods of a test.
The first quartz pressure transducer introduced by Hewlett-Packard was a surface read-out device and this
was welcomed because the pressure data could be analysed in real time as the test proceeded. However in
most DSTs currently being carried out the pressure data is recorded downhole using electronic memory
devices which are retrieved at the end of the test; this is cheaper and intrinsically more safe than the surface
read-out option which requires a cable connection to bypass the testing valve. The determination of reservoir
parameters depends on both pressure and rate being accurately measured. As the testing string is introduced
into the well, the mud or completion fluid is displaced and on setting the packer the pressure in the sealed
volume beneath attains reservoir pressure. When the valve is opened the pressure immediately changes to the
pressure in the tubing above. In order to limit the pressure differential on the formation a cushion or liquid
column is placed in the tubing as it is being run in. This cushion may be diesel oil or a heavy aqueous
solution. In some cases the whole tubing may be filled with liquid which means that the well rate is under
choke control from the start of the first flow period. When a partial cushion is used this is displaced by the
formation fluid as the well starts to flow once the testing valve is opened. Hence there is a period of rising
liquid level until liquid reaches the surface. During this period the rate of gas issuing from the well used to be
assessed by placing a hose in a bucket of water and observing the "strength of the blow". However modern
safety regulations usually prohibit such ad hoc procedures. In some tests the reservoir pressure is not
sufficient for fluids to reach the surface and the DST data is confined to a period of rising liquid level followed
by a shut-in; this is known as a slug test and special methods, which account for the rapidly decreasing rate
EPS Training
45
as the back pressure due to the rising liquid column increases, are required for interpretation. In shallow
reservoirs with competent formations the well may be tested dry i.e. with no cushion. Some operators require
that the duration of the initial, short flow period be such that, say, four times the tubing volume of reservoir
fluid be produced at the surface; this is to ensure complete displacement of the cushion from the well.
However if a heavy cushion has been employed even this precaution may not guarantee displacement.
The objectives of testing exploration or appraisal wells can be summarised as:

1. Determine the nature of the formation fluids

2. Measure well productivity

3. Measure reservoir temperature and pressure

4. Obtain samples for laboratory PVT analysis

5. Obtain information on reservoir description (permeability, heterogeneity )

6. Estimate completion efficiency i.e. skin factor

However it must be stressed that all these objectives must be subordinate to the issue of safety.
A schematic of a typical drillstem test is shown
in Figure 2.1.2 in which a dual flow period and
dual shutin are present. The purpose of the
initial short flow period - typically only five
minutes - is to relieve any supercharging (excess
pressure due to mud filtrate invasion in low
permeability formations) present and establish
communication with the reservoir. The very
short flow period ensures that negligible
depletion of the reservoir will occur even if a
small compartment is being investigated The
well is then shutin for the first buildup to
determine the initial reservoir pressure, denoted
p
i
, and the duration of this first buildup is long
enough for the pressure to essentially stabilise
so that no, or very little, extrapolation is required to fix p
i
. The well is then flowed for a long period - the
second drawdown - and shut-in for the second or final buildup. As shown in Figure 2.1.2 the rate may be
brought up in steps; this may be to investigate any sanding tendency of the formation and an acoustic sand
monitor can be installed to register the concentration of sand particles in the flowing stream. The main
objective of the second flow period is to achieve a sustained period of constant rate production prior to the
final buildup and the last flowing pressure before shutin, denoted p
wf
(t
p
), must be accurately known to allow
proper interpretation of the ensuing buildup. If the data obtained in the (second) drawdown period is analysed
the initial pressure, p
i
, is known. The design of a well test principally revolves round the decision as to how
long the major flow period should last and the question of depth of investigation of the pressure disturbance is
usually the main issue from a reservoir engineering point of view. However in the context of offshore
operations, where the expense of rig time is an important issue, there is an obvious incentive to curtail the
duration of the test. The final decision must reflect a compromise between cost and the value of additional
information gained from prolonging the test time. The issue of depth of investigation will be treated at length
later in this chapter. The duration of the final buildup should be approximately 1 times that of the preceding
flow period.
In an exploration or appraisal well test the
choice of flow-rate is governed by several
factors. For an oil well, in a prolific reservoir, the
limiting consideration is often the capacity of the
separator which will be rated, say, at 5000 or
10,000 bbl/day. In a gas well test on a
semisubmersible rig the capacity of the flare
system may well decide the maximum rate. The
Initial
Flow
I ni t i al
Shut i n
Afterflow
Final
Shutin
Final Flow
Time
Prod.
Rate
Initial Res. Pressure
Drawdown Buildup BHP
Time Figure 2.1.2
Dual Flow - Dual Shutin Test
Fig 2.1.3
4 k h
q B
s

Transient Well Testing
Buildup Analysis - Horner (Theis) Plot
Semilog Analysis
l n
t + t
p

t
Buildup
Affected
by
Wellbore
Storage Intercept
gives
skin
factor
S
Affected
by
Boundaries
ETR MTR LTR
slope =
p*
p
ws
Nomenclature
due to
D. Pozzi (EPR)
EPS Training
46
highest recorded gas well test rate offshore probably occurred in the testing of a Troll field well in Norwegian
waters where 160 million SCFD was achieved generating a drawdown of about 2 psi in the extremely permeable
and thick formation. The buildup took place over a period of about two minutes. In the testing of very high
pressure and temperature gas condensate wells in the central area of the North Sea basin, the limiting rate is
controlled by the wellhead temperature which cannot be allowed to exceed the rating of elastomers used in the
BOP stack. The well must be flowed at a low enough rate that heat loss to the surrounding rock, at geothermal
temperature, sufficiently reduces the temperature of the flowing stream as it progresses up the tubing. The
surface choke is, of course, used to limit the well rate to an acceptable value. In tight formations the rate is
controlled by the reservoir deliverability and in extreme cases no transient test is possible because a constant
stable rate cannot be sustained; this is a problem with prefracture tests in very low permeability reservoirs.
An important part of the design of a well test is to use a production engineering nodal analysis software
package to simulate the flow behaviour of the proposed system viz. tubing , choke and formation based on
estimates of the likely permeabilities which may be encountered; this exercise also requires estimates of the
PVT properties of the produced fluid.
The final buildup is usually analysed using the Horner plot illustrated diagrammatically in Figure 2.1.3; here
the bottomhole shut-in pressure, p
ws
, recorded by the transducer is plotted against a logarithmic time
function i.e.:

ln
t
p
+ t
t
. . . . . (1.1)

where t
p
is the production time and t is time measured from the moment where the well was shut in. The
theory of this interpretation method will be given later. The slope and intercept of the middle time region of the
semilog graph yield, respectively, the average permeability of the formation, k , and the skin factor, S . The
physical meaning of the skin factor has been discussed at length in Chapter 1 and is a combination of
formation damage and perforation effects as illustrated in Figure 2.1.4.
altered
zone
p
w
p
wf
p
s
Unaltered
Permeability
k
r
w
r
s
r
e
wellbore
radius
altered zone
radius
external
radius
p = I ncrement al Ski n
Pressure Drop
s
Fig
2.1.4a
k
s
Near Wellbore Altered Zone
Fig 2.1.4b
n = Number of perforations
per foot
l = Length of penetration
= Phase angle
s
p

r
w
r
s
k
s
l
p
Altered Zone
k
Combined Skin
Damage + Perforation
Perforated
Completion
S f n l k r k
s p s s
, , , , , e j

When an exploration or appraisal well is drilled the mud system will not be optimised with respect to
formation damage; for example water based muds are often employed for the appraisal wells whereas the
eventual development wells will be drilled with oil based mud which minimises alteration in water sensitive
formations. In addition exploration and appraisal wells are often drilled with a substantial overbalance which
again will result in significant mud filtrate loss promoting damage. The most important feature of transient well
testing is that the interpretation allows the independent assessment of formation average permeability, k, and
the skin factor, S. Thus even if the skin effect in the exploration/appraisal well is high the productivity index of
the future development wells can be predicted using a formula of the form:

J
sss
=
2kh
B

_
ln
r
e
r
w

3
4
+ S
. . (1.2)

where the permeability is taken from the appraisal well test and the skin factor is an estimate of what can be
achieved with optimised drilling and perforation in the future development wells. For example, in the case of
tubing conveyed perforation (TCP) in an underbalanced condition, it is possible to obtain a negative skin of
EPS Training
47
the order of -1.5. The drainage area radius, r
e
, used in this formula is related to the well spacing but it should
be noted that J
sss
is quite insensitive to the value of r
e
since it enters a logarithmic term. The important point
is that the dynamics of the transient pressure response allows a discrimination between near wellbore effects -
the skin - and the formation permeability. A simple determination of steady-state or semi-steady-state
productivity index using the defining equation:

q
s
= J
sss
(p

p
wf
) . . . . (1.3)

only requires measurement of the well flow rate, q
s
, and the corresponding flowing bottomhole pressure, p
wf
,
assuming the reservoir pressure, p

, is known. However the contributions to the resultant J

sss
due to
permeability and skin cannot be resolved without transient information i.e. a pressure buildup. The
development of pressure transient testing and, in particular, buildup analysis has been primarily motivated by
this feature of dynamic discrimination between the effects of intrinsic formation permeability and near wellbore
alteration and perforation on well productivity.
In the routine testing of development wells which have been flowing for a considerable time the main
objectives of the buildup is to determine the
current well skin factor and reservoir pressure;
this is referred to as reservoir monitoring. Again
the analysis will usually be carried out on a
Horner plot as shown on Figure 2.1.5 but using a
synthetic flowing time denoted t
sia
and the slope
may be forced to the known permeability since
this will have been determined in the first test on
the well when it was drilled. Forcing the
permeability to a known value means that the
skin factor is evaluated on a common basis and it
is possible to make a comparison between the
original and present skin factor i.e. monitor any
deterioration in well performance due to scale
deposition, fines migration, asphaltene
precipitation or any other such mechanism. The adjustment of the extrapolation of the straight line, p*, to the
reservoir pressure is known as the MBH correction and requires knowledge of any no-flow boundaries present
in the vicinity of the well. Again the theory of this approach will be given in subsequent chapters. The Horner
(semilog) buildup plot is the vehicle for such an interpretation. In the case of development wells the valve
used to shut-in the system for a buildup is located at the wellhead and the possibility of wellbore storage
effects, due to the capacity of the compressible fluid mixture in the well at the moment it is closed, must be
expected. The mechanism of wellbore storage and methods of modelling the phenomenon will be treated in
Chapter 3.
If a well is located in a closed drainage area, such as a fault block with perfectly sealing boundaries, and it is
flowed at constant rate three principle flow regimes are encountered in an extended drawdown test; these are
illustrated in Figure 2.1.6 which shows a
Cartesian plot of flowing bottom-hole
pressure versus time. The period in which
the propagating pressure disturbance has not
yet encountered any boundaries is known as
the infinite-acting or transient flow regime. It
is this data which yields a straight line on the
semilog plot, i.e. the pressure is varying with
the log of time, and it is also referred to as the
middle time region (MTR). Once the
pressure behaviour of the well is influenced
by boundaries the late time region (LTR) is
entered and in a closed system produced at
constant rate a state of semi -steady-state
(SSS) depletion as described in Chapter 1 is
eventually attained. In this flow regime the
bottom-hole flowing pressure, p
wf
, varies
E T R MT R LTR
sl ope
p*
q
4 kh
m =
l n
t + t
si a

t
p
p
ws
p
MBH
Fig
2.1.5
Horner
Plot
0
Determination of Average Pressure
WELL PRESSURE
STARTS TO BE
AFFECTED BY
BOUNDARIES
MTR LTR
TRANSIENT
I.A. FLOW TRANSITION
LATE
TRANSIENT
SEMI-STEADY-STATE
FLOW
p
i
p
wf
0
TIME
SCHEMATIC PLOT OF PRESSURE DECLINE AT
PRODUCING WELL
CONSTANT RATE WELL BOUNDED RESERVOIR
Figure 2.1.6
dp
d t
q B
c r h
s
t e

2
Cartesian Plot
Flow Regimes
MTR LTR
ln
t + t
p

depletion
buildup
drawdown
Horner
Plot
p
ws
p*
p**
Closed "tank" of
pore volume, V
Figure 2.1.7
p
i
0
Time, t
q
Detection of Depletion
EPS Training
48
linearly with time as shown in Figure 2.1.6. A well test in which the flowing period is sufficiently long for this
flow regime to be attained is termed a reservoir limit test since the size i.e. pore volume of the closed drainage
area may be found from the slope of the Cartesian plot in the SSS regime. The interval of transition between the
end of infinite-acting flow and the beginning of semi -steady-state depletion is known as the late transient
period. This transition is very short when the well is at the centre of an approximately square or circular
drainage area but becomes significant when the well is asymmetrically located or the reservoir compartment is
rectangular or triangular. Well test interpretation becomes very difficult when the infinite-acting regime is
masked, say, by wellbore storage effects. These flow regimes refer to constant rate drawdown (CRD); when a
buildup follows a period of constant rate production it is referred to as a constant rate buildup (CRB).
One of the main objectives of a drillstem test is the identification of any depletion as illustrated in Figure
2.1.7. Here the pressure attained in the final buildup is less than the initial pressure, p
i
, indicating a closed
system of finite volume. The detection of depletion depends on the correct extrapolation of the buildup to the
final stabilised pressure.
The prescription that the shut-in time, t
max
, should be 1 times the flowing time, t
p
, has the objective of
reducing the uncertainty in the extrapolation process so that it is feasible to detect any significant depletion.
In recent times the objectives of well testing have developed from the straightforward determination of an
average permeability and skin factor, to be used in the expression for productivity index, to sophisticated
approaches aimed at defining the parameters of more complex reservoir models. The progression from the
basic methodology to fuller reservoir description has been possible because of the improvements in pressure
gauge resolution allowing the use of derivative techniques and the use of interactive software packages based
on type curve matching and non-linear regression. For what might be termed category I well test interpretation
a simple model of a homogeneous reservoir
containing a vertical well with skin is sufficient;
this canonical model is illustrated in Figure 2.1.8.
Interpretation using a homogeneous model
implies that an average permeability will be
obtained when data from a heterogeneous system
is processed. The form of average e.g. arithmetic
or geometric depends on the nature of the
Skin
r
e
k
Homogeneous Finite
Reservoir
d d
Well
Image
No Flow
Boundary
k
1
k
2
r
1
Composite Infinite
Reservoir
d
2
d
1
Single Linear Fault Multiple Faults

Some Well Test Models

Fig
2.1.8
T(t=0)
x
x
Heated Bar
Thermocouples in thermowells
Transient Heat
Conduction Equation
Inner B.C.
i.e.
. . . specified
gradient
(2 kind BC)
nd
Linear Flow
t
Penetration Depth
Initial Temp.
T
Face
Temp.
Dynamic Temperature Distribution
Fig 2.1.9

T
t
k
C
T
x
p

2
2
q
A
k
T
x
x

T
x
q
kA
x

0
Constant
heat
flux
EPS Training
49
heterogeneity in the system. The integration of core analysis data with well test interpretation results
essentially revolves around the definition of such averages and the modern approach to geostatistics is giving
new insights into this activity. In a layered system for example the arithmetic average is the appropriate
method of treating core data.
In what might be classified as category II well test interpretation the methodology is extended to include the
determination of reservoir description parameters related to:

heterogeneity
boundaries
layering
anisotropy

and more complex models are required some of which are also illustrated in Figure 2.1.8.
In the 19
th
century the mathematical theory of transient heat conduction was developed based on Fouriers
equation. A temperature transient propagating in a metallic bar with constant rate heat injection at one end is
illustrated diagrammatically in Figure 2.1.9

2.2. Radial Flow Theory

2.2.1. The Basic Flow Equations

The mathematical foundation of transient pressure analysis is the theory of unsteady-state, single-phase,
one-dimensional radial flow in a porous medium. This is based on the following assumptions concerning flow
in the vicinity of the well-bore.

(1) The formation is homogeneous and isotropic with respect to both the porosity and permeability
which are also considered to be constants and thus independent of pressure.

(2) The producing well is completed across the entire formation thickness thus ensuring fully radial flow.

(3) The formation is completely saturated with a single fluid and is uniformly thick.

In certain circumstances it is necessary to partly relax these assumptions and allow for the effects of such
phenomena as non-uniform or two-phase flow or the porosity being a function of pressure. When these
effects are significant, allowance will be made by applying appropriate correction factors to the basic theory.
The basic homogeneous, radial system is illustrated in Figure 2.2.1 where the following nomenclature applies:

h = formation thickness
k = average permeability
r = general radius
r
e
= external radius of drainage area
r
w
= wellbore radius
p = pressure
q = in-situ volumetric flow-rate
t = time
u
r
= superficial velocity
= porosity
viscosity
= fluid density

The equations of motion governing the flow
follow from the principles of the conservation
of mass and momentum; the assumption is also made that the flow is isothermal. For the present purpose the
momentum equation takes the form of D'Arcy's law and the effect of turbulent or non-D'Arcy flow, which is
usually only of importance in gas reservoirs, will be taken up later. Thus the basic flow equations, in radial co-
ordinates, expressing the symmetry of the flow system, are:
h
r
e
r
w
q
Well in the
Centre of a
Ci rcul ar
Reservoi r
Radial
Flow
Fig 2.2.1
Model Reservoir
EPS Training
50

Continuity equation:
1
r

(ru
r
)
r
=

t
. . . (2.1)

Darcy's Law: u
r
=
k

p
r
. . . (2.2)

D'Arcy's law is employed as a quasi-steady approximation to the general momentum equation, i.e. a form in
which the momentum accumulation term has been discarded. This is perfectly valid provided information is not
sought concerning pressure disturbances moving at the velocity of sound in the fluid. All pressure variations
predicted by the model are associated with local pressure gradients due to laminar fluid flow. Although the
fluid compressibility will be introduced into the model sonic effects are still neglected.
In pressure analysis the flow is assumed to be horizontal and hence the pressure, p, appears in D'Arcy's law
rather than the flow potential; thus gravity forces are neglected. The superficial radial velocity, u
r
, may be
eliminated between (2.1) and (2.2) giving:


1
r

,
_
rk

p
r
r
=

t
. . . (2.3)

This is the basic partial differential equation (PDE) describing the unsteady-state flow of a single-phase fluid in
a porous medium, provided the flow is laminar. Equation (2.3) represents a general form for the combination of
the continuity equation and D'Arcy's law or the momentum equation. The PDE is non-linear because the
density, , and the viscosity, , are pressure dependent. As it stands the equation involves two dependent
variables, pressure and density, and another equation is necessary to yield a determinate system; this of
course is the equation of state relating these t wo quantities, = (p) , in an isothermal system.

2.2.2. Fluid of Constant Compressibility

The occurrence of pressure transients only takes place because the reservoir fluid is compressible to some
extent and local accumulation or depletion of fluid in the reservoir occurs. Although liquid compressibility
effects can safely be neglected in most fluid flow situations, this is not true in an oil reservoir where very large
volumes of liquid at high pressure are involved. In the case of single phase liquids the thermodynamic
equation of state is adequately represented by the model of a fluid of constant compressibility. The definition
of the compressibility, c , of a fluid is:

c =
1
V

,
_
V
p
T,m
. . . (2.4)

i.e. the relative change in the volume of the fluid per unit change in pressure; it has the dimensions of
reciprocal pressure. Equation (2.4) may be put in terms of fluid density as follows; for a constant mass of fluid,
m:

=
m
V
or V =
m

hence:
c =
1
V

V
p
=

'

;
m

p

.

_

1

p


i.e. c =
1

p
. . . . (2.5)

EPS Training
51
Not surprisingly the compressibility is also the relative change in density per unit change in pressure;
naturally if the volume decreases the density increases. For a fluid of constant compressibility equation (2.5)
may be integrated to yield:


i
e
c(p p
i
) . . . . (2.6)


where
i
is the liquid density at some reference pressure, p
i
.
Differentiating equation (2.5) with respect to time gives:

c
p
t
=

t
. . . . (2.7)

which on substitution in (2.3) results in:


1
r

.

]
1
kr

p
r
r
= c
p
t
. . (2.8)

which has achieved a partial elimination of the density from (2.3). The assumption of constant compressibility
is always valid for liquids, provided of course no gas comes out of solution, and is sometimes approximately
valid for gases at high pressures. The theory of the unsteady-state flow of real gases will be considered later.

2.2.3. Further Development of the Accumulation Term

In the derivation of the continuity equation the accumulation term represents the time rate of change of the
mass of fluid per unit superficial volume. When the porosity is not constant and varies with formation
pressure this term must be written:


()
t


which can be expanded as follows:


()
t
=

t
+

t
= c
l

p
t
+

p

.
p
t
. . (2.9)

where the liquid compressibility has been denoted c
l
. On defining the compressibility of the formation as:

c
f
=
1

p
. . . . (2.10)

this may be written:


()
t
=
( )
c
l

+ c
f

p
t
. . . (2.11)

Although in reality the on the right-hand side of equation (2.11) is still a function of pressure, as a first
approximation it can be treated as a constant evaluated at some representative average formation pressure. In
this form equation (2.11) adequately allows for the small effect of rock compressibility in all but the most
exceptional circumstances.
A further refinement of equation (2.11) is warranted; in an undersaturated reservoir two liquids are in fact
present - oil and immobile connate water - both of which are compressible. Hence the liquid compressibility, c
l
,
is given by the sum of two contributions:

c
l
= S
wc
c
w
+ S
o
c
o
. . . (2.12)

EPS Training
52
where c
w
and c
o
are the compressibilities of water and oil and S
wc
and S
o
are the respective saturations. Thus
the compressibility, c , in the basic equation (2.8) is identified with the total system compressibility, c
t
,defined
as:

c
t
= c
l
+ c
f

= S
wc
c
w
+ S
o
c
o
+ c
f
. . (2.13)


Note that the permeability, k , in equation (2.8) is not the absolute permeability of the porous medium but the
permeability to oil at the connate water saturation, i.e.

k = k
o
(S
wc
) . . . the end-point permeability

Since the flow model assumes horizontal flow the permeability also refers to this direction, i.e. it is the radial
permeability. When the total compressibility, c
t
, is employed the density, , refers to the mass per unit pore
volume of oil and connate water.

2.2.4. Linearisation of the Radial Flow Equation

The partial differential equation describing the unsteady-state, radial flow of a fluid of constant
compressibility has just been derived as:


1
r

.

]
1
kr

p
r
r
= c
t

p
t
. . . (2.14)

This form still involves two dependent variables, p and , and remains non-linear. In order to transform (2.14)
into a linear PDE in a single dependent variable, i.e. pressure, further simplifying assumptions are necessary.
Such a transformation is desirable because linear PDE's derived from (2.14) have analytical solutions which are
easily manipulated and circumvent the necessity of employing cumbersome numerical methods. The latter are
especially time-consuming when the inverse problem of non-linear parameter estimation is involved. The
additional assumptions necessary for the linearisation of (2.14) are certainly no more severe than those already
made concerning formation homogeneity etc.
For a liquid the permeability, k , and the viscosity, , are independent of pressure and equation (2.14) may be
written:


1
r

.

{r
p
r
}
r
=
c
t

k

.

p
t
. . (2.15)

The derivative term on the left-hand side of (2.15) may be expanded using the chain rule for differentiation;
thus:


1
r

_
r

2
p
r
2
+
p
r
+ r
p
r

.

r
=
c
t

k

.

p
t
. (2.16)

The compressibility is defined as:

c
t
=
1

p
. . . . (2.17)

and differentiating this equation with respect to 'r' results in:

r
= c
t

p
r
. . . . (2.18)

Substitution of (2.18) in (2.16) gives:

EPS Training
53

1
r

_
r

2
p
r
2
+
p
r
+ rc
t

,
_
p
r
2
=
c
t

k

.

p
t
(2.19)

The assumption is now made that the pressure gradient p/r is small and hence (p/r)
2
can safely be
neglected. Under this assumption, and cancelling throughout, equation (2.19) becomes:

2
p
r
2
+
1
r

p
r
=
c
t

k

.

p
t
. . . (2.20a)

or, alternatively:


1
r

,
_
r
p
r
r
=
c
t

k

.

p
t
. . . (2.20b)

For the flow of liquids the above assumptions are quite reasonable and have frequently been applied.
However this simple linearisation by deletion must be treated with caution and can only be applied when the
following condition is satisfied:

c
t
p << 1 . . . . . (2.21)

For example when the c
t
p product is 0.1 the solutions of (2.19) and (2.20) differ by about 5%. This condition
makes it necessary to modify the assumption concerning compressibility such that it is not just constant but
both small and constant. When dealing with reservoir systems which have a high compressibility, so that
(2.21) is not valid, it is necessary to linearise (2.21) or its equivalent using some form of mathematical
transformation. Such an approach will be required when dealing with a gas reservoir, since in this case the
compressibility of the gas alone, assuming it to be ideal, is the reciprocal of the pressure; hence to a first
approximation the c
t
p product is unity and condition (2.21) is certainly not satisfied.

2.2.5. Initial and Boundary Conditions

The linearised radial flow equation :


p
t
=
k
c
t

.

1
r

.

,
_
r
p
r
r


is a second-order, linear, parabolic PDE having pressure as the dependent variable and radial position and time
as the independent variables. Similar second-order parabolic equations of this form are frequently encountered
in the theory of diffusional transport processes, e.g. unsteady-state heat conduction, and all equations of this
type are referred to as 'the diffusivity equation'. Hence the quantity k/(c
t
) is known as the hydraulic
diffusivity, , and has dimensions L
2
T
-1
. However it should be emphasised that there is no diffusional
aspect to D'Arcy's law and its similarity to Fourier's law of heat conduction, for example, is purely mathematical.
Fortunately, because of its importance in transport phenomena, almost every conceivable analytical solution to
the diffusivity equation is available in the literature.
In order to determine the solution of a second-order PDE of the parabolic type an initial condition and two
boundary conditions must be specified. The fundamental solutions of interest in the development of pressure
analysis methods are those for the case of flow into a centrally located well at a constant volumetric rate of
production, q. Later on it will be demonstrated how the principle of superposition may be used to yield
solutions for arbitrary rate histories. The geometry of the system is again shown in Figure 2.2.1; the reservoir
is assumed to be cylindrical in shape with thickness, h , and ext ernal radius, r
e
. The well is of radius r
w
and in
all cases of interest r
w
<< r
e
.

(a) Initial Condition

EPS Training
54
Before any flow into the well takes place the whole cylindrical element is assumed to be at the uniform initial
reservoir pressure, p
i
. Using the notation p(r,t) to represent the pressure as a general function of radial
position, r , and time, t , the initial condition may be written succinctly as:

p(r, o-) = p
i
, r
w
r r
e
. . . (2.22)

Here o- signifies any time prior to t = 0.

(b) Boundary Condition at the Well Bore - Constant Rate Inner Boundary Condition

At time t = 0 the well is set in production at a constant volumetric flow-rate, q
s
, and maintained at this level
from then on. This oil flow-rate, q
s
, is measured at stock tank conditions and hence the in situ reservoir flow
rate is given by q = q
s
B where B is the oil formation volume factor. Although this latter quantity is a weak
function of pressure it is treated as a constant, evaluated at the initial reservoir pressure. Applying D'Arcy's
law just inside the formation at the sand face gives:

u
r
r=r
w
=
q
s
B
2r
w
h
=
k

p
r
r=r
w

or, on re-arranging:


p
r
r=r
w
=
q
s
B
2kh

.

1
r
w
, t o . . . (2.23)

This imposes a constraint on the formation pressure gradient at the well-bore and is known as a boundary
condition of the second kind. For all ordinary purposes the finite wellbore radius boundary condition (2.23)
may be replaced by the alternative form:


Lim
ro

,
_
r
p
r
=
q
s
B
2kh
, t > o . . (2.24)

which is known as the 'line source' approximation to the original condition. This has been shown to yield
identical results (from a practical standpoint) to those obtained from solution of the problem with the exact,
less-tractable version. The line source approximation assumes the well-bore radius to be vanishingly small and
is acceptable because the dimension of the well-bore is very small compared to the radius of the volume
drained by the well. When fractured wells are treated as cylindrical wells of large effective radius the full finite
wellbore radius solution must be employed; this is really the only occasion when the line source
approximation is not valid.

(c) External Boundary Condition

Three distinct forms of external boundary condition arise, each one pertaining to a different physical situation.
Naturally each specific boundary condition yields its own unique solution to the PDE. The three basic cases
of interest are:

(1) Infinite Reservoir

In this case the well is assumed to be situated in a porous medium of infinite radial extent. This condition is
also valid for a reservoir of finite size provided any pressure disturbance generated at the well never reaches
the outer boundary of the reservoir which remains at the initial pressure, p
i
, throughout the period of interest.
This condition may be written:

p(r, t) = p
i
as r , t > o . . (2.25)

(2) Bounded Reservoir
EPS Training
55

In this case the well is assumed to be located in the centre of a cylindrical reservoir of radius r
e
with no flow
across the exterior boundary. The no-flow condition implies zero superficial velocity at the outer boundary
and hence the local pressure gradient must also be zero, i.e.


p
r
r=r
e
= 0 , t > 0 . . . . (2.26)

(3) Constant Pressure Outer Boundary

Here the well is situated in the centre of a cylindrical area with a constant pressure, equal to the initial pressure,
p
i
, maintained along the outer boundary. This condition takes the form:

p(r
e
, t) = p
i
, t > 0 . . . . (2.27)

The specific application of each of these cases will become apparent later.

2.2.6. Dimensionless Form of the Diffusivity Equation

The linearised partial differential equation of compressible fluid flow in a porous medium, embodying the
principle of mass conservation and D'Arcy's law, takes the form:


p
t
=
1
r

.

,
_
r
p
r
r
. . . . (2.28)

where =
k
c
t
= hydraulic diffusivity.

A typical set of initial and boundary conditions (infinite reservoir case) are:


I.C. at t < 0 : p = p
i
for all r (2.29)

B.C.1 at r = r
w
:
p
r
=
q
s
B
2kh

.

1
r
w
for all t o (2.30)

B.C.2 at r = : p = p
i
for all t o (2.31)

The solution to the problem is a mapping p(r,t) representing the pressure as a function of position and time;
naturally the solution p(r,t) must satisfy both the differential equation and the prescribed initial and boundary
conditions which in combination are referred to as the differential system. The constants appearing in this
system, e.g. , p
i
and the quantity q
s
B /(2kh) are known as the system parameters and these must be
specified before a particular solution can be obtained. However, it is much preferable first to obtain a general
analytical solution which is quite independent of any specific values given to the parameters. Once this is
available any particular solution, corresponding to a certain set of parameter values, is readily obtainable. The
general solution is achieved by transforming the differential system into dimensionless form. This is a
standard procedure in engineering mathematics and should always be carried out where possible.
When the solution in terms of pressure, p(r,t) , has been established the remaining variables, if required,
follow from D'Arcy's law and the equation of state, i.e.

u
r
(r, t) =
k

{p(r,t)}
r
. . . . (2.32)

EPS Training
56
(r, t) =
i
exp[ ] c
t
(p (r, t) p
i
) . (2.33)

In order to understand the philosophy behind the procedure for rendering the system dimensionless it is
helpful to consider briefly the nature of solutions
to the diffusivity equation. Some typical pressure
profiles in a cylindrical reservoir at various times
following the well being set in production are
shown in Figure 2.2.2; initially the reservoir was
everywhere at pressure p
i
.
At early time the pressure disturbance, due to
fluid expansion and motion, is localised in a region
around the central well but this progressively
propagates itself further out into the reservoir.
The difference in pressure between the initial
value, p
i
, and that in the well (r = r
w
) is known as
the drawdown and increases with the depth of
penetration of the pressure disturbance into the
formation. Note that, at the well-bore, the gradient
of the pressure profile is identical at all times, which is indicative of the constant flow-rate boundary condition.
The time taken for the leading edge of the pressure disturbance to reach a radial position, r, is given
approximately by :

t
r
= 0.1
r
2

. . . . (2.34)

and the quantity:

t
w
=
r
2
w

. . . . (2.35)


can be regarded as a characteristic time constant of the system. For a reservoir of finite size, the infinite
reservoir solution will be valid for all times 't' such that:

t < 0.1 t
e
= 0.1
r
2
e

i.e. t
De
=
t
D
r
2
De
=
kt
c
t
r
2
e
< 0.1 . . (2.36)

which is the condition that the pressure disturbance has not yet reached the external boundary to any
significant extent.
Thus choosing r
w
as a characteristic dimension of the system and t
w
as a characteristic time it is possible to
define the dimensionless independent variables r
D
and t
D
as follows:

r
D
=
r
r
w
. . . . . (2.37)

t
D
=
t
t
w
=
t
r
2
w


ln r
t
p( r , t )
p
i
Well-
Bore
Tr ansi ent Devel opment of
t he For mat i on Pr essur e
Di st r i but i on
Fig 2.2.2
EPS Training
57
or t
D
=
kt
c
t
r
2
w
. . . . . (2.38)

When considering the dependent variable, i.e. pressure, p , it is convenient to form dimensionless ratios by
dividing by the quantity q
s
B/(2kh) suggested by the inner boundary condition. Also, in order to ensure
that the dimensionless boundary conditions assume as compact a form as possible, it is preferable to formulate
the system in terms of pressure deviation from the initial value. Hence the dimensionless pressure (difference)
is defined as:

p
D
=
p
i
p
q
s
B
2kh
=
2kh
q
s
B
(p
i
p) . . . (2.39)

This is equivalent to measuring pressure relative to a datum of p
i
. Note that 'q
s
' is positive for production and
a positive p
D
represents drawdown.
Making the substitutions:

t =
t
D
r
2
w

r = r
D
r
w
p = p
i

q
s
B
2kh
p
D


into equations (2.28), (2.29), (2.30) and (2.31) the dimensionless differential system becomes:


p
D
t
D
=
1
r
D

,
_
r
D

p
D
r
D
r
D
. . . (2.40)

I.C. at t
D
< 0 p
D
= 0 for all r
D
(2.41)

B.C.1 at r
D
= 1,
p
D
r
D
= 1 for all t
D
> 0 (2.42)

B.C.2 at r
D
= , p
D
= 0 for all t
D
> 0 (2.43)

The differential system has now been put into fundamental form amenable to solution by the standard
mathematical methods for linear parabolic PDEs of the diffusivity type. The general analytical solution to the
system can be obtained without any reference to the physical situation it represents. In this systems
engineering approach the mathematical analysis, i.e. the mechanics of deriving the solution, whether by
analytical or numerical methods, is completely divorced from the engineering aspects concerned with setting
up equations which adequately describe the physical situation and interpreting the solution once it is
available. Indeed it may be preferable to rewrite the system using the conventional nomenclature of the
mathematical literature, e.g.


x
t
=
1
z

{z
x
z
}
z
z > 1

t < 0 , x = 0 all z
(2.44)
z = 1 ,
x
z
= 1 all t > 0

z = , x = 0 all t > 0

EPS Training
58
where x is the dependent variable and 't' and 'z' are the independent time and space variables respectively. In
this way the problem is posed as a purely mathematical one.
The analytical solution of the dimensionless differential system is denoted p
D
(r
D
, t
D
), or equivalently x(z, t),
and represents the general solution to the basic system for all values of the parameters and dimensions. A
particular solution is easily obtained from the general solution using equation (2.39), i.e.

p(r, t) = p
i

q
s
B
2kh
p
D

_
r
r
w

,

t
r
2
w
. . (2.45)


2.2.7. The Line Source Analytical Solution in an Infinite Reservoir

For this case the dimensionless differential system takes the form:


p
D
t
D
=
1
r
D

_
r
D

p
D
r
D
r
D
r
D
> 0 . (2.46)

t
D
< 0, p
D
= 0 all r
D



Lim
r
D
0

_
r
D

p
D
r
D
= 1 all t
D
> 0

r
D
= , p
D
= 0 all t
D
> 0

The analytical solution of this problem is given in many textbooks concerned with transport phenomena, e.g.
Carslaw and Jaeger
(7)
. In 1949 Hurst and van Everdingen
(8)
presented a comprehensive description of the
solution of the radial diffusivity equation applicable to reservoir engineering problems. Their solutions were
obtained by applying the Laplace transformation to the diffusivity equation primarily in order to solve the
problem of water influx into a radial reservoir from a similarly shaped aquifer of both finite and infinite extent.
The flow of reservoir fluids into the well-bore has precisely the same nature as the flow of water into a radial
reservoir but on a different scale. A more concise analytical solution of the present problem, not involving
Laplace transformations has been quoted by Matthews and Russell. Only the result of these analyses will be
given here and the references can be consulted for further details if required.
The analytical solution of the differential system (2.46) is:

p
D
(r
D
, t
D
) =
1
2
i

_

r
2
D
4t
D
. . . (2.47)

where Ei(x) is a standard mathematical function called the exponential integral which is defined by:

i(-x) =

e
-u
u
du . . . . (2.48a)


7
Carslaw, H.S. and Jaeger, J.C.:"The Conduction of Heat in Solids", 1959, Clarendon Press, Oxford (2
nd

Edition)
8
van Everdingen, A.F. and Hurst, W.:"The Application of the Laplace Transformation to Flow
Problems in Reservoirs", Trans AIME (1949), 186, 305-324
EPS Training
59
i(x) =

e
-u
u
du . . . (2.48b)


and hence Ei( x) = Ei(x). The Ei
function is tabulated in mathematical
data books and is shown, plotted on a
log-log scale, in Figure 2.2.3; Ei(x) is
large for small values of x and vice-
versa. Fortunately when x is small, i.e.
x < 0.01, the exponential integral is
very closely approximated by a simple
logarithmic function given below; thus
for x < 0.01:







Ei(x) = Ei(x) = ln( x) . . . (2.49)

where is Eulers constant and has a value of 1.781 or e
0.5772
. Hence the general analytical solution may be
written in the simpler form:

p
D
(r
D
, t
D
) =
1
2
ln

_
r
2
D
4t
D
. . (2.50)

or, on re-arranging and entering the numerical value of :

p
D
(r
D
, t
D
) =
1
2

]
1
ln (t
D
/r
2
D
) + 0.80907 . (2.51)

The latter equation is, of course, only valid when:


r
2
D
4t
D
< 0.01

Fortunately this is nearly always the case in connection with pressure testing when the wellbore pressure at r
D

= 1 is required and hence (2.51) is the most useful form of the analytical solution.
The solution in terms of the actual variables and system parameters follows from the equation:

p(r, t) = p
i

q
s
B
2kh
p
D

_
r
r
w

,

t
r
2
w
. . (2.52)

Noting that:


r
2
D
t
D
=
r
2
t
=
c
t
r
2
kt
. . . (2.53)

10
4
10
5
10
6
10
7
10
8
10
9
10
1
10
-1
10
-2
10
-1
1 10 10
2
10
3
10
4
p
D
t /r
D D
2
Figure 2.2.3
Single Well in an Infinite Reservoir
(No Skin)
Exponential Integral Solution
EPS Training
60
the exact solution becomes:

p(r, t) = p
i

q
s
B
2kh

_

1
2
i

_

c
t
r
2
4kt
. . (2.54)

and the approximate version:

p(r, t) = p
i

q
s
B
2kh

.

1
2

_
ln
kt
c
t
r
2
+ 0.80907 . (2.55)

The condition that the latter is valid may be written:


kt
c
t
r
2
> 25

Indeed when kt/(c
t
r
2
) is equal to 5 the error in using the log approximation is still only about 2%. Note that
for values of t
D
/r
D
2
less than 5 the line-source solution based on the Ei function starts to deviate from the
solution to the radial diffusivity corresponding to the proper boundary condition (2.24).
The preceding equations give the pressure as a general function of both time and position in the reservoir.
However in most applications the important item of interest is the pressure at the well-bore; this is the
observable quantity in well tests. The dimensionless well-bore pressure, i.e. that corresponding to r
D
= 1 is
given by:

p
D
(1, t
D
) =
1
2
[ln t
D
+ 0.80907] . . (2.56)

It is convenient to represent the pressure just inside the homogeneous formation adjacent to the well-bore by
the symbol p
w
and hence from equation (2.55):

p
w
(t) = p(r
w
, t) = p
i

q
s
B
2kh

.

1
2

]
1
1
1
ln
kt
c
t
r
2
w
+ 0.80907 (2.57)

2.2.8. Well-bore Damage and Improvement Effects

In the preceding treatment only the dynamic pressure behaviour within the homogeneous formation has been
analysed. It is now necessary to relate the pressure in the well-bore itself, i.e. the bottom-hole fluid pressure as
measured by a transducer, to that in the adjacent
formation, p
w
. The bottom-hole fluid pressure at
the mid-point of the producing interval in a
flowing well is denoted p
wf
. In general the two
quantities p
w
and p
wf
are not identical because
of the method of completing the well. The
phenomenon of skin effect and well-bore damage
or improvement has already been introduced in
Chapter 1 and discussed at length in the
treatment of steady-state flow. One way of
quantifying such damage to operating wells
represents the well-bore condition by a steady-
state pressure drop at the well-face in addition to
the normal pressure profile in the formation: this
is illustrated in Figure 2.2.4. The incremental
pressure drop called the 'skin effect' is presumed to occur over an infinitesimally thin 'skin zone' in which the
permeability impairment is confined. Accordingly, the bottom-hole flowing pressure is given by:
p
s
p
w
p
wf
"SKIN"
t
PRESSURE PROFILE
I N THE FORMATI ON
r
w
NEGATIVE SKIN
FACTOR
i.e. STIMULATION
p
s
p
wf
pw
k > k
a
PRESSURE PROFILE
IN FORMATION
RIGOROUS SKIN
CONCEPT PROFILE
t
STIMULATED ZONE
Figure 2.2.4
Dimensionless
Skin
S
p
q B
kh
s
s

2
Positive Skin
Factor
i.e. Damage
EPS Training
61

p
wf
(t) = p
w
(t) + p
s
. . . (2.58)

where the skin pressure drop, p
s
, is a function of the instantaneous well flow-rate, q
s
B , the fluid viscosity,
, and the characteristics of the altered zone, i.e. its average radial thickness and permeability. The important
assumption is made that, since the skin is so thin there is insignificant accumulation or depletion of fluid in this
region and hence quasi-steady-state conditions exist. For all practical purposes the skin pressure drop reacts
immediately to any changes in production rate, e.g. if the flow stops p
s
disappears without delay. Of course
even at constant flow-rate long term changes in p
s
can occur due to progressive plugging of the well-face,
hence the term 'quasi-steady-state'.
The dimensionless skin pressure drop is denoted by S and is defined by the equation:

S =
p
s
q
s
B
2kh
. . . . (2.59)

Since the pressure drop over the damaged zone, assuming steady-state laminar D'Arcy flow, should be
proportional to the product q
s
B the dimensionless skin factor, S, only depends on the nature of the
impairment. The dimensionless form of equation (2.58) may now be written:

p
D
(1-, t
D
) = p
D
(1, t
D
) + S . . (2.60)

where the notation r
D
= 1- implies pressure in the well-bore. Hence the dimensionless working equations for
transient flow with a well-bore skin effect take the form:

p
D
(1-, t
D
) = p
wfD
=
1
2
[ln t
D
+ 0.80908 + 2S] (2.61)

and the corresponding equation in actual variables and parameters becomes:

p
wf
(t) = p
i

q
s
B
2kh

.

1
2

]
1
1
1
ln
kt
c
t
r
2
w
+ 0.80908 + 2S (2.62)

This formulation is the basis for constant rate drawdown analysis on a semilog graph illustrated in Figure 2.2.5
in which the permeability is obtained from the slope and the skin factor from the intercept.
EPS Training
62
CRD
p
i
0
q
p
wf
TIME, t
0
CARTESIAN PLOT
INTERCEPT
SLOPE, m
ln t
0
p
wf
SEMILOG PLOT
Figure 2.2.5
=
q
4 kh
p (t=1)
wf
Rate Schedule
Ideal (CSFR) Drawdown


2.2.9. Analytical Solution for the Case of a Bounded Circular Reservoir

Of course no real reservoir is infinite in extent and the solution of the preceding section is only valid while
the pressure transient is confined within the limits of a particular cylindrical volume. As soon as the pressure
at the outer boundary starts to deviate from the initial value one of the external boundary conditions becomes
operative. Usually the alternative form most consistent with physical reality is the no flow constraint (2.26).
Occasionally the mathematical boundary may coincide with a physical barrier, i.e. the extremity of the reservoir.
However, a much more common situation arises when several producing wells, placed more or less
symmetrically, are distributed over the reservoir. In this case no flow boundaries arise because of the reservoir
drainage patterns which develop; deviation from the transient, infinite reservoir solution occurs when the
expanding, radially symmetric pressure disturbances from adjacent wells first come in contact. The concept of
drainage volumes will be taken up in detail later.
In the meantime an individual well will be assumed to be located in the centre of a cylindrically shaped
drainage area of uniform thickness, h , and external radius, r
e
, with no flow across the external boundary. The
dimensionless differential system now takes the form:


p
D
t
D
=
1
r
D

_
r
D

p
D
r
D
r
D
1 r
D
r
De (2.63)


t
D
< 0 , p
D
= 0 all r
D


r
D
= 1 ,
p
D
r
D
= 1 all t
D
> 0

EPS Training
63
r
D
= r
De
,
p
D
r
D
= 0 all t
D
> 0

where r
De
=
r
e
r
w
.
The derivation of the analytical solution, using the Laplace transform technique, to this differential system is
also given by Matthews and Russell and the result is:

p
D
(r
D
, t
D
) =
2
r
2
De
1

_
r
2
D
4
+ t
e

r
2
De
lnr
D
r
2
De
1



(3r
4
De

4r
4
De
lnr
De
2r
2
De
1)
4(r
2
De
1)
+


m=1

exp (
2
m
t
D
) J
2
1
(
m
r
De
) A

m
[J
1
2
(
m
r
De
) J
1
2
(
m
)]


. . . (2.64)

where A = J
1
(
m
)Y
0
(
m
r
D
) Y
1
(
m
)J
0
(
m
r
D
)

and
m
are the roots of:

J
1
(
m
r
De
)Y
1
(
m
) J
1
(
m
)Y
1
(
m
r
De
) = 0 . (2.65)

For the dimensionless pressure at the well-bore, r
D
= 1 , and for the case where r
e
>> r
w
, i.e. r
De
>> 1 ,
equation (2.64) simplifies considerably and can be written:

p
D
(1, t
D
) =
2t
D
r
2
De
+ ln r
De

3
4
+

2
m=1

exp(
2
m
t
D
) J
2
1
(
m
r
De
)

m
2

]
1
J
2
1
(
m
r
De
) J
2
1
(
m
)
. (2.66)

The
m
values in equations (2.64) or (2.66) take on monotonically increasing values as 'm' increases, i.e.
1
<

2
. . . . . . <
m
. . . . Thus for a given value of t
D
the exponentials decrease monotonically. Also the Bessel
function portion of the terms in the series becomes less as 'm' increases. Hence as t
D
becomes large, the terms
for large 'm' become progressively smaller and the summation is rapidly convergent. Indeed for sufficiently
large t
D
all the terms of the series are negligibly small; for practical purposes this occurs for t
D
/r
De
2
greater
than about 0.3, i.e. if the following condition is satisfied:

t
De
=
t
D
r
2
De
=
kt
c
t
r
2
e
> 0.3 . . (2.67)

the dimensionless pressure is given by equation (2.64) without the series summation and hence becomes a
linear function of t
D
. In this case p
D
/t
D
is a constant, irrespective of position, which implies that the
EPS Training
64
dimensionless pressure is changing at the same rate everywhere in the system and that the pressure profiles
are therefore not altering in shape as time proceeds. This situation is described as the semi -steady-state or
pseudo-steady-state flow period and the dimensionless pressure at the well-bore during this period is given
by:

p
D
(1, t
D
) =
2t
D
r
2
De
+ ln r
De

3
4
. . (2.68)

The concept of semi -steady-state is an important one and is treated at length subsequently. It has already
been indicated that for values of the parameter t
D
/r
De
2
less than 0.1 the pressure disturbance has not yet
reached the outer boundary at r
e
and the solutions to systems (2.46) and (2.63) are indistinguishable provided
the line-source approximation is valid. Thus when the dual condition

t
De
< 0.1
t
D
r
2
D
> 5 . . (2.69)

is satisfied the bounded reservoir solution (2.64) may be replaced by the mathematically much simpler line-
source, infinite-reservoir solution (2.47). Naturally when t
D
/r
D
2
> 25 the logarithmic approximation to the
exponential integral, i.e. equation (2.51), is preferable. The pressure behaviour in this period is not affected by
the external boundary and is essentially the same as in an infinite reservoir; this is described as transient flow
or the infinite acting period.
The interim time during which neither the infinite acting nor the semi-steady-state asymptotes are applicable
to the pressure behaviour of the bounded reservoir is known as the late transient period and occurs when:

0.1 < t
De
< 0.3 . . . (2.70)

Thus the pressure behaviour domain is divided into three distinct regimes viz. transient, late transient and
semi-steady-state each corresponding to a specific physical state of the reservoir.
Condition (2.36), upon which conditions (2.69) and (2.70) are partially founded, was arrived at by considering
the error in the predicted pressure at the external boundary. If it is only the pressure at the well-bore which is
of concern the infinite acting solution is acceptable for a bounded, circular reservoir over a longer period of
time. Indeed up to values of t
De
of 0.3 the deviation between the values of well-bore pressure predicted by
equations (2.56) and (2.66) is less than 1%. Hence, in a circular drainage area with a central well, for all practical
purposes regarding the well-bore pressure there are only two flow regimes - the infinite acting and semi-
steady-state periods - with the demarcation occurring at t
De
equal to 0.3. Thus in summary:

Circular, Bounded Reservoir, Well-bore Pressure

(a) t
De
< 0.3 : Transient flow

p
D
(1, t
D
) =
1
2
[ln t
D
+ 0.80907] . . (2.71)

(b) t
De
< 0.3 : Semi-steady-state flow

p
D
(1, t
D
) =
2t
D
r
2
De
+ ln r
De
-
3
4
. . (2.68)

This is very convenient since the complicated late transient solution involving Bessel functions need not be
employed. Alternatively in terms of actual variables and parameters these become:

(a) t <
0.3c
t
t
r
2
e
k
: Transient flow
EPS Training
65

p
w
(t) = p
i

q
s
B
2kh

.

1
2

]
1
1
1
ln
kt
c
t
r
2
w
+ 0.80907 . (2.57)
(b) t >
0.3c
t
r
2
e
k
: Semi-steady-state flow

p
w
(t) = p
i

q
s
B
2kh

]
1
1
1

2kt
c
t

r
2
e
+ ln
r
e
r
w

3
4
. (2.72)

2.2.10. Analytical Solution for a Constant Pressure Outer Boundary

In this event the condition at the external limit takes the form:

r
D
= r
De
, p
D
= 0 all t
D
. . (2.73)

and inflow through the outer boundary takes place at a rate determined by the local pressure gradient and
D'Arcy's law, i.e.

p
r
r=r
e
=
q
e
B
2khr
e
. . . . (2.74)

where q
e
is the inflow from a sink surrounding the cylindrical volume. Using the definitions of dimensionless
quantities equation (2.74) may be written:

q
e
= q

p
D
r
D r
D
=r
De
. . . . (2.75)

For the moment only the analytical solution for the dimensionless well-bore pressure will be given, i.e.

p
D
(1, t
D
) = ln r
De

2
m=1

exp(
2
m
t
D
) J
2
o
(
m
r
De
)

2
m

]
1
J
2
1
(
m
) J
2
o
(
m
r
De
)
. (2.76)

where the
m
are the roots of:

J
1
(
m
) Y
0
(
m
r
De
) Y
1
(
m
) J
0
(
m
r
De
) = 0 (2.77)

Again for sufficiently long times the summation is negligible and equation (2.76) reduces to:

p
D
(1, t
D
) = ln r
De
. . . (2.78)

or, in terms of actual variables

p
w
= p
i

q
s
B
2kh
ln
r
e
r
w
. . . (2.79)

In this circumstance the inflow at the external boundary and the production rate are equal, i.e. q
e
= q
s
and a
true steady-state exists within the cylindrical volume. Note that in equation (2.79) p
i
represents the pressure at
the outer boundary and is synonymous with p
e
.

EPS Training
66
2.2.11. SPE Field Units

In the preceding treatment the equations have been presented in fundamental form applicable in any system
of consistent units e.g. strict metric S.I. where the basic units are:

Production rate, q
s
: m
3
/s Formation thickness, h : m Permeability, k : m
2

Viscosity, : Ns/m
2
Pressure, p : Pa Radius, r : m
Time, t : s Compressibility, c
t
: Pa
-1


Table 2.1 S.I. Metric Units

However most engineers prefer to work in a more practical system of units, for example SPE field units which
are defined as:

q
s
: STbbl/day h : ft k : md
: cp p : psia r : ft
t : hr c
t
: psia
-1


Table 2.2 SPE Field Units

In terms of SPE field units the definitions of dimensionless pressure and time take the form:

p
D
=
2khp
887.2q
s
B
t
D
=
0.0002637kt
c
t
r
2
w


and any equation can be converted into field units using the appropriate definit ions of p
D
and t
D
.

2.2.12. The Depth of Investigation and Radius of Drainage

These analytical solutions to the diffusivity
equation predict the dynamic response of the
pressure in a model reservoir after it is put on
production at a constant rate, q. The
pressure response to a variable (time-
dependent) production rate will be
considered subsequently. The distributed
pressure behaviour of the reservoir is
conveniently represented on a plot of
pressure drop versus radial distance from t he
well-bore at particular times, all on a
dimensionless basis; such a diagram is
shown in Figure 2.2.6. In order to compute
this information it is necessary to evaluate
the full exponential integral solution using an
algorithm of the form:

0 x 1

Ei(x) = ln x + a
0
+ a
1
x + a
2
x
2
+ a
3
x
3
+ a
4
x
4
+ a
5
x
5
+ (x)

where a
0
= 0.57721566 a
3
= 0.05519968
a
1
= 0.99999193 a
4
= 0.00976004 (x) < 210
-7

a
2
= 0.24991055 a
5
= 0.00107857

1 x
10
4
10
5
5x10
5
10
6
2x10
6
t = 3x 10 D
6
0
1
2
3
4
5
6
7
8
9
1 200 400 600 800 1000
r
D
p
D
r =10
De
3
Figure
2.2.6
Dimensionless Pressure Distributions in Radial Flow
SSS
I A
Well in a
Closed
Reservoir
EPS Training
67

Ei(x) =
1
xe
x

.

x
4
+ a
1
x
3
+ a
2
x
2
+ a
3
x + a
4
x
4
+ b
1
x
3
+ b
2
x
2
+ b
3
x + b
4
+ (x)

where a
1
= 8.5733287401 b
1
= 9.5733223454
a
2
= 18.059016973 b
2
= 25.6329561486 (x) < 210
-8

a
3
= 8.6347608925 b
3
= 21.0996530827
a
4
= 0.2677737343 b
4
= 3.9584969228

The Ei function has the form shown in Figure 2.2.7; as the argument, x, becomes large the function
asymptotically approaches zero. Note that
the region in which the log approximation is
valid occurs at very small values of the
argument viz. x < 0.01. The exponential
function is mainly required for the
interpretation of well to well interference
tests where the radius, r, is the distance
between observation and active well.
When the well is put on flow at time t = 0
the oil production rate, q , is initially
sustained by the expansion of fluid
immediately around the well-bore. However
this expansion is, of course, accompanied
by a reduction in pressure and a local
pressure gradient is established in the
reservoir. Thus fluid from the next adjacent
annular zone flows toward the well-bore at a rate governed by D'Arcy's law and the process of fluid expansion-
pressure decline is extended further into the reservoir. In this way a progressively increasing zone of pressure
drawdown propagates out from the active well until it reaches the external boundary. The propagation of this
pressure disturbance is analogous to the temperature transient in a cylindrical block of material subjected to a
constant heat flux at the face of a central cavity. Since the well is produced at a constant rate the pressure
gradient at the well-bore, r = r
w
, is the same at all times. The shape of the instantaneous pressure profile at
any time during the transient period is still much influenced by the radial nature of the flow, i.e. rapidly
increasing gradient as the well-bore is approached, and this results in the well-bore pressure exhibiting the
strongest dynamic response to a well flow-rate change. In most transient well tests this is precisely the
quantity which is observable by measurement using down-hole pressure recording instruments.
In Figure 2.2.6 the dimensionless pressure profiles at t
D
= 10
3
, 10
4
and 10
5
have been constructed using the
exponential integral solution i.e. equation (2.47); the dimensionless pressure, p
D
, is plotted as a function of
dimensionless radius, r
D
, for various values of dimensionless time, t
D
. It is not until t
D
/r
2
De
= 0.1, equivalent
to t
D
= 10
5
in this reservoir, that the external boundary pressure starts to decline and the exponential integral
solution is invalid. The profiles for t
D
= 510
5
and greater have been computed from the semi -steady-state
solution and it is apparent how the pressure decline takes place uniformly without change in the shape of the
distribution. For dimensionless times between t
D
= 10
5
and 510
5
strictly speaking the bounded reservoir (late
transient) solution should be employed but, as previously stated, there is very little error in omitting this
regime; the graphical presentation of the pressure behaviour shows no signs of discontinuity between infinite-
acting and semi-steady-state behaviour. Remember, however, that this is only true for a well in the centre of a
circular drainage area.
During the infinite-acting period a region of pressure disturbance propagates out from the well at which a
flow-rate change has occurred. This penetration aspect is quite characteristic of systems whose behaviour is
described by the second-order, parabolic diffusivity equation and is well-known in heat conduction and mass
transfer. The analogy between diffusional t ransport processes and compressible fluid flow in a porous medium
derives from the similar mathematical nature of underlying phenomenological description.
For example, the basis of unsteady-state heat conduction is:

(a) local flux equation (Fourier's law)
q
A
= k
dT
dr

HENCE E(x) IS DENOTED -Ei (-x) 1
1
2
3
0.4 1.0 1.6
E (x)
1
-Ei(-x)
0
x
Fig 2.2.7
Ei x
e
u
u
x
ej

z
Exponential Integral Function
EPS Training
68

(b) relation between energy density
and temperature (state equation) de = C
p
dT

(c) law of energy conservation

whereas compressible fluid flow is described by:

(a) local flux equation (D'Arcy's law)
q
A
=
k

dp
dr


(b) relation between mass density and
pressure (state equation) d = c dp

(c) law of mass conservation

Although compressible fluid flow in porous
media is not diffusional in nature the governing
equations have the same mathematical form.
Because of the importance of the diffusivity
equation in transport phenomena, analytical or
numerical solutions exist for almost every
conceivable geometry and boundary condition.
The velocity with which the pressure
disturbance moves out through the reservoir is
determined by the system hydraulic diffusivity,
= k/(c
t
). The leading edge of the pressure
front, defined loosely as the location where the
pressure is say 1% different from the initial value,
is shown in Figure 2.2.8. The dimensionless
pressure drop at a distance, r
D
, from the wellbore and at time, t
D
,

is given by the exponential integral solution:

p
D
=
1
2
Ei

_
r
2
D
4t
D


If the argument of the Ei function is arbitrarily set to unity, i.e.
r
2
D
4t
D
= 1 , the value of p
D
is given by:

p
D
(r
Di
) =
1
2
Ei(1) =
0.2194
2
= 0.11

This implies that at any time, t
D
, the dimensionless pressure drop is less than 0.1 at a distance r
Di
from the
wellbore where:

r
Di
=
r
i
r
w
= 4t
D
=
4kt
c
t
r
2
w
. . . (2.80)

Thus the depth of penetration in radial geometry is given by:

r
i
= 4 t =
4kt
c
t
. . . (2.81)

10
3
5x10
3
t=10 D
4
1 100 200
r
D
PRESSURE
DISTURBANCE
FRONT
Fig 2.2.8
Radius of Influence
p = 0. 1
D
EPS Training
69
Although this definition of depth of investigation or radius of influence is borrowed from transient heat
conduction, where it is termed depth of penetration, the concept is extremely useful in well test analysis and is
a measure of the extent of the reservoir which has been influenced by the pressure disturbance. Equation (2.81)
may also be written in the alternative dimensionless form:

t
Di
=
t
D
r
2
Di
=
kt
c
t
r
2
i
= 0.25 . . (2.82)

The definition of the radius of investigation is somewhat arbitrary since the pressure profile is in fact
asymptotic to p
i
and no sharp front exists. Hence the value of the constant in (2.82), for example, depends on
the level of deviation from p
i
which is chosen to be significant. The value of 0.25 has been accepted as
defining the reservoir volume which has contributed to the dynamic pressure response measured at the well-
bore. Taking the constant as 0.1, as suggested previously, would seriously overestimate the region which had
any real influence on pressure at the well-bore. In SPE field units equation (2.81) becomes:

r
i
=
40.0002637kt
c
t
=
0.00105kt
c
t
= 0.032
kt
c
t
(2.83)

In practical terms, since the porosity, , and the compressibility, c
t
, do not vary very much the dynamic
pressure response is largely determined by the reservoir permeability, k, and the oil viscosity, . The
implication of this statement is that, if the response to a flow-rate change is measured and the oil viscosity is
known, it should be possible to infer the value of the reservoir permeability. This is one of the main objectives
of transient well testing.
The concept of depth of investigation is particularly useful in estimating how far from a well information is
being obtained at a particular time in a transient well test. In addition, it is of vital importance in estimating the
duration of a proposed well test to evaluate the entire drainage area of a well.
The nature of the transient pressure response is further illuminated by considering the behaviour of a well to
well interference test illustrated in Figure 2.2.9
where the pressure is measured in an inactive
observation well some distance, r, from the
flowing well. The pressure at the observation
well, again modelled by the exponential integral
solution, is also plotted as a function of time in
Figure 2.2.9. Since sonic phenomena are
disregarded in the diffusivity equation the
analytical solution predicts that the pressure at
the observation well starts to change immediately
the active well is set in flow. In reality, of course,
pressure disturbances cannot exceed the speed of
sound in the porous medium. However the
pressure propagation process essentially follows
a diffusional model and after some time the
dimensionless pressure change at the observation well, p
D
, exceeds the arbitrary value of 0.1; at this point the
depth of investigation is deemed to have reached the observation well. It is readily apparent from this physical
situation that the actual moment at which a pressure change at the observation well becomes detectable is
related to the resolution of the pressure transducer; once the pressure deviation from p
i
becomes larger than
the gauge resolution, p, it is resolvable. In Chapter 4 an alternative definition of depth of investigation, based
on pressure transducer resolution, will be given.
A related concept to depth of investigation is
that of radius of drainage which is illustrated in
Figure 2.2.10 where the dimensionless pressure
profile at some time, t
D
, is plotted versus ln r
D
.
Over a large range of r
D
the pressure profile
exhibits a straight line on this plot indicating that
quasi-steady-state conditions exist in the vicinity
q
ACTIVE
WELL
OBSERVATION
WELL
MINIMUM OBSERVABLE p
DEPENDS ON GAUGE RESOLUTION

r
D
"ARBITRARY"
CRITERION
Ei SOLUTION
p
i
p
wo
OBS
WELL
PRESSURE
0
t
Fig 2.2.9
p Ei
r
t
D
D
D

F
H
G
I
K
J
1
2 4
2
p
p kh
q
D

2
01

.
Depth
of
Investigation
1
2
3
4
5
6
p
D
0 1 2 3 4 5 6 7
ln r
D
Radius
of
Drainage
r
D
Fig 2.2.10
I.-A. Transient
Pressure Profile
at t = 10
D
5
Steady-State
Pressure Profile
for Same p(1,t )
D
D
r
Dd
r
D i
r = classical depth
of investigation
D i
EPS Training
70
of the wellbore i.e. the pressure distribution follows the steady-state model:






(p(r,t) p
wf
(t))2kh
q
s
B
= ln
r
r
w
. . . (2.84)

The radius of drainage is defined through the equivalent annulus having the same overall steady-state
pressure drop as the dynamic case; thus:

p
D
(1,t
D
) =
(p
i
p
wf
(t))2kh
q
s
B
=
1
2
ln
4t
D

= ln r
Dd
= ln
r
d
r
w
. (2.85)

i.e.
1
2
ln
4 t
r
2
w
= ln
r
d
r
w


r
d
=
1

4 t = 0.7493 4 t

which corresponds to r
d
= 0.75r
i
. Thus the radius of drainage, r
d
, is somewhat smaller than the classical
depth of investigation, r
i
.
This definition of radius of drainage corresponds to finding the intercept, r
Dd
, of the straight line portion of
the dynamic pressure profile shown in Figure 2.2.10. The important fact emerges that the flow conditions in the
vicinity of the wellbore conform to quasi-steady-state implying that the local flow-rate, q
r
, is indistinguishable
from the fixed sand-face rate, q , over quite a range of radii; this implies that there is negligible expansion of
fluid occurring in the near wellbore region. This observation is crucial in the understanding of multiphase flow,
for example, and the behaviour of radial composite systems.
The idea of radius of drainage is closely related to the concept of transient productivity index denoted J
t
and
defined by the equation:

q
s
= J
t
(p
i
p
wf
(t)) . . . . (2.86)

Comparing this definition with the transient flow expression including a skin effect:

p
D
(t
D
) =
(p
i
p
wf
(t))2kh
q
s
B
=
1
2

_
ln
4kt
c
t
r
2
w
+ 2S (2.87)

J
t
is given by:

J
t
=
2kh
B

_

1
2
ln
4kt
c
t
r
2
w
+ S
=
2kh
B

_
ln
r
d
r
w
+ S
. (2.88)

Thus the transient productivity index is just another way of expressing the p
D
function and serves to
demonstrate that the transient PI, as defined above, decreases with time as the pressure disturbance
propagates out into the reservoir. Note that the concept of transient PI is very useful when the pressure drop
or drawdown is held approximately constant and the rate declines as a consequence of the sandface pressure
gradient decreasing as the disturbance moves deeper into the system. Note that J
t
is defined in terms of the
initial pressure, p
i
, since the notion of average pressure really has no meaning in an infinite-acting system.

EPS Training
71
2.2.13. The Dynamics of Reservoir Pressure Response

The theoretical well-bore pressure response for the same reservoir (r
De
= 1000) is shown in more detail in
Figure 2.2.11 where the dimensionless pressure drop, p
wD
, is plotted against dimensionless time, t
D
, on both
logarithmic and linear scales. During the infinite-acting period when the logarithmic approximation to the
t = 0.3 De
r = 1000
De
4
2
0
t = 10 D
t = 25
D
p
wD
ln t
D
1 10 10
2
10
3
10
4
10
5
10
6
0 2 x 10
3
4 x 10
3
6 x 10
3
8 x 10
3
10 x 10
3
0
1
2
3
4
5
p
wD
PRODUCTION
SHUT-IN
0
q
0
t
D
0 2 4 6 8 10 12 14
6
8
10
Cartesian Graph
t
D
t
D
Semilog Plot
Pressure Drawdown at the Wellbore
Fig 2.2.11
Ei function is valid the dimensionless pressure drop (for t he case of zero skin) is given by:

p
wD
=
1
2
[ ln t
D
+ 0.80908] . . . (2.56)

and this is clearly shown as a straight line on the semi -log plot (Figure 2.2.11(a) ). Equation (2.56) is applicable
when t
D
> 25 and t
De
< 0.3 as indicated. For t
D
between 10 and 25 the proper exponential integral solution
should be used and for t
D
< 10 the line source solution (dotted line on Figure 2.2.11(a) ) must be replaced by
one based on a finite well-bore radius shown in Figure 2.2.12. Note that it is not valid to extrapolate the linear
portion of the semi-log plot back to early times.
For values of t
De
greater than 0.3 the semi-steady-state solution:

p
wD
=
2t
D
r
2
De
+ ln r
De

3
4
. . . (2.68)

is applicable and the well-bore pressure declines more rapidly than the prediction of the infinite-acting model.
Hence the theoretical pressure response falls below the extrapolation of the linear portion of the semi -log plot
as indicated on Figure 2.2.12(a).
Figure 2.2.12(b) shows a direct plot of well-bore drawdown versus time on a dimensionless basis and
demonstrates the very rapid initial rate of change of pressure when the well is put on production. Figure 2.1.6
delineates the three flow regimes and illustrates that in the SSS regime the plot of well-bore pressure versus
time is linear.
The addition of the skin effect to the semi -steady-state flow equation results in:

p
D
(1-, t
D
) = p
wfD
=
2t
D
r
2
De
+ ln r
De

3
4
+ S . (2.89)

and the corresponding equation in actual variables and parameters becomes for semi -steady-state flow:


EPS Training
72
p
wf
(t) = p
i

q
s
B
2kh

]
1
1
1

2kt
c
t
r
2
e
+ ln
r
e
r
w

3
4
+ S (2.90)
where
p
wfD
= p
D
(1-, t
D
) =
p
i
p
wf
q
s
B
2kh


The pressure distribution in the reservoir during the SSS period is illustrated in Figure 2.2.13 where the
stabilised shape of the pressure profiles at successive times is apparent.
r
D
= 1.0
2
. 0
1
.
2
2
0
EXPONENTIAL INTEGRAL
SOLUTION
10
-2
10
-1
1 10 10
2
10
3
10
-2
10
-1
1
10
p
D
t /r
D
2
D
Finite Wellbore Radius Solution
Finite Wellbore Radius (FWR) Solution
Fig 2.2.12
p
p
e
p
wf
Stabilised
Pressure
Distribution
SSS Depletion
Wel l i n Centre of a
Cl osed Ci rcul ar Reservoi r
r
e
r
w
Fig 2.2.13 Pore Vol ume = hA
q
s

2.3. Pressure Drawdown Testing

2.3.1. Introduction

The analytical solution to the diffusivity equation for a uniform pressure initial condition and a constant
flow-rate inner boundary condition has led to an expression for the dynamic well-bore pressure behaviour of a
model reservoir having homogeneous formation permeability and instantaneous skin effect. The objective of a
well test is to measure the dynamic response of an actual reservoir under these same conditions and determine
unknown reservoir parameters by inference. The two most important such parameters are the permeability
thickness product, kh , and the skin factor, S. The productivity of a well can only be predicted if these
quantities are known. The problem of well testing is essentially one of parameter estimation in which the
unknown properties are adjusted until the theoretical solution or ideal model matches the measured system
behaviour. In linear systems this can often be achieved directly without a search process.
Often the first significant transient event at an oil well is the initial production period that results in a
pressure drawdown at the formation face. Provided the production rate can be controlled at a constant value,
the physical situation corresponds to the model conditions and thus it seems logical to investigate what can
be learned about the well and the reservoir from pressure drawdown data. In this section constant-rate
drawdown testing in the infinite-acting and semi-steady-state flow regimes will be considered. Although
drawdown testing is not limited to the initial productive period of a well, that may be the ideal time to obtain
drawdown data.
Figure 2.3.1 schematically illustrates the production and pressure history during a drawdown test. Ideally the
well is shut-in until it reaches static reservoir pressure before the test. This requirement is met in new
reservoirs; it is less often met in old reservoirs.
The drawdown test is run by producing the well at
a constant flow-rate while continuously recording
bottom-hole pressure. While most reservoir
information obtained from a drawdown test can
also be obtained from a pressure build-up test,
there is an economic advantage to drawdown
testing since the well is produced during the test.
The main technical advantage of drawdown
TIME, t
Pressure Drawdown Testing
RATE
q
0
0
SHUT-I N
PRODUCING
TIME, t
p = p ws i
0
Fig
2.3.1
Bottom
Hole
Pressure
p
wf
EPS Training
73
testing is the possibility of estimating reservoir volume. The major disadvantage is the difficulty of
maintaining a constant production rate and the fact that the skin factor, S, may change due to the well cleaning
up.

2.3.2. Pressure Drawdown Analysis in Infinite-Acting Reservoirs

The bottom-hole pressure at an active well producing at a constant rate in an infinite-acting reservoir is given
by equation (3.1):

p
wfD
=
1
2
[ ] lnt
D
+ 0.80908 + 2S . (3.1)

or in terms of actual variables:

p
wf
= p
i

q
s
B
2kh

.

1
2

]
1
1
1
ln
kt
c
t
r
2
w
+ 0.80908 + 2S . (3.2)
i.e.

p
wf
= p
i

q
s
B
2kh

.

1
2

]
1
1
1
lnt + ln
k
c
t
r
2
w
+ 0.80908 + 2S (3.3)

if the reservoir is at p
i
initially; here t is the time from the start of production. Theoretically a plot of measured
flowing bottom-hole pressure versus the natural logarithm of flowing time (commonly called the semilog plot)
should be a straight line of slope m and intercept p
t=1
- when lnt = 0, t = 1. Hence the analysis of drawdown
data consists of making a plot of p
wf
against lnt giving:

p
wf
= m lnt + p
t=1
. . . (3.4)

Such a graph is shown in Figure 2.3.2; from equation (3.3) the slope is given by:

m =
q
s
B
4kh
. . . . (3.5)

and the intercept corresponding to lnt equal to 0 by:

p
t=1
= p
i
+ m

]
1
1
1
ln
k
c
t
r
2
w
+ 0.80908 + 2S . (3.6)

Once the slope of the straight line portion of the semilog plot, m, has been determined the permeability
thickness product, kh , can be calculated from equation (3.5). This presumes, of course, that the oil production
rate, q
s
, has been measured in the test and that the oil formation volume factor, B, and viscosity, , are
known from laboratory PVT studies. If the formation thickness (net pay), h , is known from log evaluation the
formation permeability, k , can be obtained. Equation (3.6) may be rearranged as an explicit expression for the
skin factor, i.e.

S =
1
2

]
1
1
1
p
t=1
p
i
m
ln
k
c
t
r
2
w
0.80908 . . (3.7)

Hence if the initial reservoir pressure, p
i
, the porosity, , the total compressibility, c
t
, and the well-bore
radius, r
w
, are known the skin factor can be calculated from the slope and intercept of the plot using equation
EPS Training
74
(3.7). Note that both the numerator and the denominator in the first term in the brackets in equation (3.7) are
intrinsically negative.
It is apparent from Figure 2.3.2 that the data points corresponding to early times do not coincide with the
fitted linear portion of the semilog plot. Indeed theory suggests early points should lie below the straight line
whereas the initial measured data falls
considerably above it. This deviation from ideal
behaviour is due to well-bore storage and damage
effects. The theoretical model envisages a step
change in the oil flow-rate at the well-face at time
t=0. However in practice it is impossible to
achieve such an instantaneous change and the
well-face flow changes from zero to the final value
over a finite time interval. Even if the surface oil
rate could be rapidly set at the desired constant
value the compressibility of the large amount of
fluid in the well-bore will sustain the initial
production and the actual well-face flow will lag
significantly behind the surface flow. This
phenomenon is known as well-bore storage and
will be treated in detail in the next chapter.
The influence of well-bore storage is compounded by the presence of a skin effect. In principle the bottom-
hole pressure should decline by an amount p
s
immediately the well is put on production. However, because
of the lag in the build-up of well-face flow the skin pressure drop does not reach its full value instantaneously.
In fact there is also some capacity associated with the skin zone itself and this further contributes to a delay in
the establishment of p
s
. Thus the deviation of the early data points from the idealised model is a result of the
combination of well-bore storage and skin effects. Before determining the slope and the intercept of the fitted
straight line it is essential to exclude all points affected by these phenomena. A rational method for doing this
based on a log-log plot will be given in Chapter 3 on well-bore storage. Note that the intercept, p
t=1
, must be
determined by extrapolation of the linear trend on the semilog graph. Once the data points influenced by well-
bore storage and damage have been eliminated from consideration, the most convenient way of determining
the best slope and intercept is to use a least-squares linear regression routine. However it is essential that the
plotted data be first examined visually for anomalous points.
The preceding equations can be used with either of the sets of consistent units. However, within the oil
industry, there is still a preference for using field units and the working equations are easily transformed to
accommodate this. The field units version of equation (3.3) is:

p
wf
= p
i

887.217q
s
B
2kh.2

]
1
1
1
ln
0.0002637kt
c
t
r
2
w
+ 0.80908 + 2S
. . . (3.8)
or on rearranging:

p
wf
= p
i

70.6q
s
B
kh

]
1
1
1
lnt + ln
k
c
t
r
2
w
7.43173 + 2S
. . . (3.9)

Hence, in field units, a plot of p
wf
(psi) versus lnt (t:hr) gives a straight line of slope, m , and intercept, p
t=1

where:

m =
70.6 q
s
B
kh
. . . . (3.10)

and

0
p
t=1
ln t
NOTE : ln t = 0 corresponds to t = 1
Fig 2.3.2
Deviation from straight line
caused by damage and
wellbore storage effects
slope, m =
4 k h
q B s
Drawdown Semilog Plot
Bottom
Hole
Pressure
p
wf
EPS Training
75
p
t=1
= p
i
+ m

]
1
1
1
ln
k
c
t
r
2
w
7.43173 + 2S . (3.11)

which on solving for the skin factor, S, becomes:

S =
1
2

]
1
1
1
p
t=1
p
i
m
ln
k
c
t
r
2
w
+ 7.43173 . (3.12)

The preceding treatment is based on the usage of the natural logarithm, lnt , and advocates plotting p
wf

against lnt on ordinary linear graph paper; this approach is more amenable to analysis using least-squares
regression procedures. The natural log is fundamental to the basic theory and the working equations are
simpler if it is retained. However, it is also possible to plot p
wf
versus t directly on semilog graph paper and
this approach has been much used in the past. Hence it is necessary to derive the equations on the basis of
log to the base ten on which logarithmic graph paper is founded. The dimensionless drawdown equation is:

p
wfD
=
1
2
ln
4t
D

+ S . . . . (3.13)

which on converting to log
10
becomes:

p
wfD
=
2.3026
2

]
1
1
log
4t
D

+ 0.86859 S . . (3.14)

Changing to actual variables in field units this becomes:

p
wf
= p
i

887.217q
s
B
2kh

.

2.3026
2

]
1
1
1
log
0.00026374kt
c
t
r
2
w

+ 0.86859 S
. . . . . (3.15)

and the working equations in field units and log
10
become:

m =
162.6 q
s
B
kh
psi/log cycle . . . (3.16)


p
t=1
= p
i
+ m

]
1
1
1
log
k
c
t
r
2
w
3.2275 + 0.86859 S
. . . . (3.17)

S = 1.1513

]
1
1
1
p
t=1
p
i
m
log
k
c
t
r
2
w
+ 3.2275 . (3.18)

Again in equation (3.18) p
t=1
must be from the semilog straight line. If pressure data measured at 1 hour do
not fall on that line, the line must be extrapolated to 1 hour and the extrapolated value of p
t=1
must be used in
equation (3.18). This procedure is necessary to avoid calculating an incorrect skin by using a well-bore
storage influenced pressure.
If the drawdown test is long enough, the bottom-hole flowing pressure will eventually deviate from the
semilog straight line and make the transition from infinite-acting to semi-steady-state behaviour.
EPS Training
76
Although a properly run drawdown test yields considerable information about the reservoir the test may be
hard to control since it is a flowing test. If a constant rate cannot be maintained within a reasonable tolerance
the analysis technique presented in this section cannot be used. Variable rate procedures are considered in
Chapter 6. Another practical problem is that of measuring accurately the small pressure drops encountered, at
the fairly high absolute pressures involved.

2.4. The Principle of Superposition

2.4.1. Introduction

The analytical solutions developed for the diffusivity equation in section 2 were all for the idealised case of a
single well operating at a constant rate from time zero onward. Since real reservoir systems usually have
several wells operating at varying rates, a more general approach is needed to study problems associated with
transient well testing. Fortunately, because the diffusivity equation is linear, variable-rate, multiple well
problems can be handled by applying the principle of superposition. The constant rate inner boundary
condition takes the form:

r = r
w
,
p
r
=
q
s
B
2khr
w


in which the well production rate, q
s
, remains unchanged throughout the whole production history. Except
under special test conditions this will not normally be the case and flowing well rates may change because of
demand variation or altered reservoir conditions. Some well tests, by their very nature, involve variable rate
and production histories, e.g. short drill stem tests or offshore exploratory well tests. In the general case the
well production rate is time dependent and should be written q(t). The inner boundary condition now takes the
form:

r = r
w
,
p
r
=
q
s
(t)B
2khr
w
. . . (4.1)

and the dynamic pressure behaviour of the reservoir under such a time dependent boundary condition is
obviously much more complex than in the simple constant rate case.
The superposition principle states that adding solutions to a linear differential equation results in a new
solution to that differential equation, but for different boundary conditions. Superposition can be applied to
include more than one well, to change rates and to impose physical boundaries. Superposition is easily
applied to infinite systems but for bounded
systems it must be used with more care - not
because the principle is different but because the
basic solutions frequently do not give the
necessary information
for correct superposition.

2.4.2. Multiple-Well Situations

The simplest illustration of superposition is that
of determining the pressure drop at some point in a
field in which two sinks are located. Consider the
three well infinite system shown in Figure 2.4.1. At
time t = 0 well 1 starts producing at rate q
1
and well
2 starts producing at rate q
2
. It is desired to determine the pressure at the shut-in observation point, well 3. To
do this the pressure change at well 3 caused by well 1 is added to the pressure change at well 3 caused by well
2, i.e.


p
3
= p
3,1
+ p
3,2
. . . (4.2)

o
Well 1
q
1
Well 2
q
2
r
1
r
2
Well 3
Observation Well
Active Well
Three Well System
Figure 2.4.1
Principle of Superposition
EPS Training
77
In order to utilise equation (4.2) expressions for the individual pressure drops of the form:

p
i,j
=
q
i
B
j

2kh
p
D
(t
D
, r
Dj
) . . . (4.3)

must be employed with the appropriate well flow-rate, q
j
B
j
, and dimensionless distance, r
Dj
, to the
observation point, i , for each sink, j . Thus equation (4.2) may be written:

p
3
=

2kh
(q
1
B
1
p
D
(t
D
, r
D1
) + q
2
B
2
p
D
(t
D
,r
D2
)) . . (4.4)

which can be extended to an arbitrary number of wells:

p(t,r) =

2kh

j=1
n
q
j
B
j
p
D
(t
D
, r
Dj
) . (4.5)

Note that equation (4.5) adds pressure changes (or dimensionless pressures). If the point of interest is an
operating well the skin factor must be added to the dimensionless pressure for that well only. If the wells do
not all start producing at the same time t
D
in equation (4.5) should be replaced by t
Dj
, the dimensionless
production time for each individual well. There is no restriction on the number or location of sinks (or sources)
and it is perfectly valid to consider two or more sinks as coincident, i.e. at the same point in space in order to
generate a variable rate history at this point.

2.4.3. Variable Rate Situations

To illustrate the application of the principle of superposition to varying flow-rates, consider a single well
system with the production rate schedule shown in Figure 2.4.2.
q
2
q
t
T
1
q - q
2 1
Two-Rate Flow Schedule
Fig 2.4.2
Injection well
rate q q
2 1

Production well
rate q
1
Superposition of Rates
Total Response
Extrapolated
Pressure
Principle of Superposition
Injection Well
at Rate q - q
2 1
Well at
Rate q1
0
T
1
t
0
p p
i w

p
DD
p
DD
Fig
2.4.3
The oil flow-rate is q
1
from t = 0 to t = t
1
, and q
2
thereafter. To perform the superposition calculation the
single well may be visualised as two wells located at the same point, with one producing at rate q
1
, from t = 0
to t and the second (imaginary) well producing at rate (q
2
- q
1
), starting at t
1
and continuing for a time period (t
- t
1
). The net superposed rate after time t
1
would be q
1
+ (q
2
- q
1
) = q
2
as desired. As in the previous example
delta-p's are added for these conditions. The general form of the equation for N rates, with changes at t
j
, j = 1,
2 . . N, is:

p =

2kh

j=1
N
{(q
j
B
j
q
j-1
B
j-1
)(p
wD
(t t
j-1
)
D
+ S)} . (4.6)

where (t-t
j
)
D
is the dimensionless time calculated at time (t-t
j
).
For the rate schedule of Figure 2.4.2, N=2, only two terms of the summation are needed and equation (4.6)
becomes:

EPS Training
78
p =
B
2kh
{q
1
(p
wD
(t
D
) + S) + (q
2
q
1
)(p
wD
(t
D
t
D1
) + S)}
. . . . (4.7)

Figure 2.4.3 illustrates the calculation i.e. superposition. The lower dashed curve (including the first portion of
the solid curve) is the pressure change caused by rate q
1
, alone. The topmost curve is the pressure change
caused by the rate q
2
- q
1
, after t
1
; that p is negative because (q
2
- q
1
) < 0. The sum of the dashed curve and
topmost curve is the pressure response for the two-rate schedule.

2.5. Pressure Build-Up Testing

2.5.1. Introduction

The most widely used form of transient well testing technique is pressure build-up analysis. This type of
testing was first introduced by groundwater hydrologists but it has been extensively used in the petroleum
industry. Pressure build-up testing entails shutting in a producing well and recording the closed-in bottom-
hole pressure as a function of time. The most common and simplest analysis techniques require that the well
produce at a constant rate, either from start-up or long enough to establish a stabilised pressure distribution
before shut-in. If possible the flowing bottom-hole pressure prior to shut-in should also be recorded; indeed it
is essential if an estimate of skin is required.
Figure 2.5.1 schematically shows flow-rate and
bottom-hole pressure behaviour for an ideal
pressure build-up test. Here t
p
is the production
time and t is the running shut-in time. The
pressure is measured immediately before shut-in
and is recorded as a function of time during the
shut-in period. The resulting pressure build-up
curve is analysed for reservoir properties and
well-bore condition.
As in all transient well tests, knowledge of
surface and subsurface mechanical conditions is
important in build-up test data interpretation.
Therefore it is recommended that tubing and
casing sizes, choke size, well depth, packer
locations etc be determined before data
interpretation starts. Short -time pressure observations are usually necessary for complete delineation of well-
bore storage effects. Data may be needed at intervals as short as 15 seconds for the first few minutes of some
build-up tests. As the test progresses, the data collection interval can be extended. Stabilising the well at a
constant rate before testing is an important part of a pressure build-up test. If stabilisation is overlooked or is
impossible, conventional analysis techniques may provide erroneous information about the formation. Thus it
is important to determine the degree and adequacy of the stabilisation; one way is to check the length of the
pre-shut-in constant rate period against the time required to reach semi -steady state flow, i.e. q
De
= 0.3 for a
central well. For wells with significantly varying rates before shut-in, build-up test analysis is still possible
using the variable-rate methods discussed later.
If the well produces at a constant rate, q , for a time,t
p
, and pressures are subsequently recorded for closed-
in times, t , then the bottom-hole pressure at any time after the well has been shut-in can be obtained from a
superposed solution based on:

q acting for time (t
p
+ t) + (o q) acting for time t

The build-up test rate schedule is the simplest form of two-rate test (q
2
= 0) and the two-rate superposition
formula:

p =
B
2kh
{ q
1
[ ] p
wD
(t
D
) + S + (q
2
q
1
) [ ] p
wD
(t
D
t
1D
) + S }
R
A
T
E
t
p

t
t
FLOWING
SHUT-IN
t p
B
H
P
p
ws
p ( t=0)
wf

Figure
2.5.1
Schematic Flow-Rate and Pressure Behaviour for an Ideal Buildup
q
EPS Training
79
. . . (5.1)

will predict the pressure behaviour during the second zero rate period; on putting:

q
1
= q
s
; q
2
q
1
= q
s
; t
D
= t
pD
+ t
D
; t
D
t
1D
= t
D


this becomes:

p =
q
s
B
2kh
{ p
wD
(t
pD
+

t
D
) p
wD
(t
D
) }

i.e.
p
ws
(t) = p
i

q
s
B
2kh
{ p
wD
(t
pD
+

t
D
) p
wD
(t
D
) } (5.2)

where p
wD
is the applicable dimensionless pressure function; note that the shut-in pressure, p
ws
, is not
affected by the skin factor in an ideal build-up test. Equation (5.2) provides the theoretical basis for the
analysis of pressure build-up tests.

2.5.2. Pressure Build-Up Test Analysis during the Infinite-Acting Period

There are several ways for analysing the results of a build-up test the most popular being the Horner method
which is based on the supposition that the reservoir is infinite in extent and a negligible amount of fluid is
removed from the system during the production period prior to closure. In practice this case corresponds to an
initial well test conducted in a virgin reservoir. During an infinite-acting period both dimensionless pressure
terms in equation (5.2) are replaced by the logarithmic approximation to the exponential integral, i.e.

p
wD
(t
D
) =
1
2
(lnt
D
+ 0.80908)

and equation (5.2) becomes:

p
ws
(t) = p
i

q
s
B
2kh

.

1
2
(ln(t
pD
+ t
D
) ln t
D
)

or
p
ws
(t) = p
i

q
s
B
2kh
ln
t
p
+ t
t
. . . (5.3)

This is the Horner build-up equation which predicts a linear relationship between p
ws
and ln((t
p
+ t)/t) ;
note that the ratio is independent of the units of the time quantities. This equation also indicates that, for an
infinite-acting system, the bottom-hole shut-in pressure will eventually build up to the initial reservoir
pressure, p
i
. Equation (5.3) describes a straight line of the form:

p
ws
= m ln
t
p
+ t
t
+ p* . . . (5.4)

with slope m =
q
s
B
4kh
. . . . (5.5)

and intercept, p* = p
i
. . . . (5.6)

In this case the intercept, p*, corresponds to ln((t
p
+ t)/t) equal to zero or (t
p
+ t)/t = 1 which implies
t >> t
p
- a shut-in time very long compared to the production time. From such a plot the reservoir average
permeability can be obtained as:
EPS Training
80

k =
q
s
B
4mh
. . . . (5.7)

provided all the quantities on the right-hand side of (5.7) are known. In oilfield units equation (5.3) becomes:

p
ws
(t) = p
i

70.6q
s
B
kh
ln
t
p
+ t
t
. . (5.8)
or
p
ws
(t) = p
i

162.6q
s
B
kh
log
t
p
+ t
t
. (5.9)

The most important feature of the semilog plot is that the reservoir kh product can be determined from the
slope of the build-up. This is a much better value than can be obtained by trying to average core measured
permeabilities over the entire producing interval.
The determination of the permeability is the most significant result to be obtained from an initial test on a
reservoir simply because, under these circumstances, the initial pressure could be obtained from a spot
measurement prior to opening the well in the first place. Once the well has been producing for a significant
period of time this statement is no longer true because the well will now have produced an amount of fluid
which may not be insignificant in comparison to the initial oil in place. Therefore it can no longer be assumed
that the pressure will build up to its initial value even for an infinite closed-in time, but rather to some lower
value p which will be representative of the average pressure within the drainage volume of the well. This
corresponds to pressure build-up in a bounded reservoir which will be considered later.
It is instructive to examine the process of pressure build-up within the reservoir itself as well as at the well-
bore. Defining the dimensionless reservoir pressure after shut-in as:

p
sD
= p
sD
(r
D
, t
D
) =
p
i
p
s
(r, t)
q
s
B
2kh
. . (5.10)

the superposition theorem states that:

p
sD
= p
D
(r
D
, t
pD
+ t
D
) p
D
(r
D
, t
D
) . (5.11)

However at locations far removed from the well-bore the logarithmic approximation is not valid and the
dimensionless pressure functions on the right-hand side of (5.11) must be represented by the proper
exponential integral solution for an infinite-acting system. The dimensionless shut-in pressure distribution for
an infinite reservoir which has produced for a dimensionless production time of t
pD
= 10
4
is shown in Figure
2.5.2; this diagram was drawn in accordance with equation (5.11) using Ei functions for the p
D
terms. When
the well is shut-in the inner boundary condition becomes one of no flow, i.e. zero pressure gradient at the well-
bore. This is clearly seen in Figure 2.5.2 from the pressure profiles at various values of the dimensionless shut-
in time, t
D
all these have zero slope at r
D
= 1.
p
ws
ln
t + t p
t
p*
Devi ati on from Strai ght
Line caused by
Afterflow and Skin
0
slope, m =
4 k h
q B
s

Semilog (Horner) Plot for a Buildup
Fig 2.5.1b
r
D
0
5
1 200
q
0
t
p D
tD
t = 10
pD
4
Pressure Build-Up in a Reservoir
Figure 2.5.2
t = 10
D
4

10
50
200
2 10
3
p
sD

EPS Training
81
This is in marked contrast to the pressure profiles during flowing periods which have very steep slopes. Fluid
continues flowing toward the well after shut-in but since it cannot emerge from the reservoir this fluid
accumulates which it can only do by compressing and the reservoir pressure rises. This process continues
until the pressure is everywhere equalised. However it is apparent from Figure 2.5.2 that the final stages of
pressure recovery are slow because reservoir pressure gradients are small and fluid flow is difficult. The
behaviour of the closed-in well-bore dimensionless pressure is shown in more detail in Figures 2.5.3 and 2.5.4.
0
4
0 7
l n

t
D
t
D
t + pD
0
5
p
sD
t
D
10 10
3
10
3
5 1 0
3
t = 10
p D
4
Pressure Build-Up
at Wellbore
Semilog
Cartesian
Dimensionless
Response
(Horner)
Fig 2.5.3
p
sD
t + t
p

t
13 5
2
6
t
D
t = 10
pD
4
t < 10
D
Ei Function not
Represented by
Log Approximation
Fig 2.5.4
p
D
Dimensionless Build-up Semilog (Horner) Plot

Figure 2.5.3 demonstrates theoretically the linearity of the Horner plot for dimensionless shut-in times, t
D
,
greater than 10. However for values of t
D
less 10 it is no longer valid to use the logarithmic approximation to
the exponential integral solution. Thus for very early shut-in times:

p
wsD
= p
D
(tp
D
+ t
D
) p
D
(t
D
)
1
2
ln
t
p
+ t
t


In fact:
p
wsD
=
1
2
(ln(t
pD
+ t
D
) + 0.80908) +
1
2
i

,
_
1
4t
D
. (5.12)

Figure 2.5.4 shows the behaviour of p
wsD
at very early shut-in times evaluation using (5.12) and it can be seen
that the exact solution deviates from the extrapolation of the linear portion; clearly such an extrapolation is not
valid. In theory then one would expect early build-up points to lie above the straight line. In practice they
often fall below the line and the reason for this is again the effect of well-bore storage and skin.

2.5.3. After Production

The preceding theory of pressure build-up analysis is based on the supposition that the oil flow-rate at the
well-face can be instantaneously reduced from the constant rate, q , to zero. Often the well is shut-in at the
surface and pressure increases in the well-bore after shut-in require the influx of sufficient fluid fromthe
formation to compress the contents of the whole well-bore. Note however that, in drill stem tests or offshore
exploration well tests on semi-submersible rigs or drill ships, the closing-in valve is at bottom-hole. The
duration and magnitude of this effect, called afterflow in pressure build-up testing, depends on the flow-rate
before shut-in, the capacity of the well-bore and the fluid compressibility. The effect is minimised when the
well production rate is high and hence in highly productive wells afterflow is not a serious problem. In general
it is advisable always to avoid analysis of pressure build-up data for times when bottom-hole pressures are
affected by after production.
Thus even though the well is shut-in during pressure build-up testing, the afterflow caused by well-bore
storage has a significant influence on pressure build-up data. Figure 2.5.5 shows that the pressure points fall
below the semilog straight line while well-bore storage is important. Two effects cause this less than ideal rate
of pressure build-up. Firstly pressure build-up in the formation itself is less rapid because of the continuing
production from the well-face. Secondly the skin pressure drop, which should disappear instantaneously at
the moment of closure, declines in response to the afterflow.
EPS Training
82
t + t
p

t
Effect of Afterflow on a Horner Plot
Data Affected
by Wel l bore
St orage
Correct Semilog
Straight Line
p
ws
0
p*
slope m
Fig 2.5.5
ETR MTR
1
1000
0.001 100
t
p
(psi)
Unit
Slope
Dat a of Cor r ect
Semi l og Sl ope
(hr)
Fig 2.5.6
MTR
Log - Log Diagnostic Plot for Afterflow

The duration of these effects may be estimated by making the log-log data plot described in Chapter 3 on
well-bore storage. For pressure build-up testing, plot log [p
ws
- p
wf
(t = 0)] versus log t. When well-bore
storage dominates that plot will have a unit slope straight line; as the semilog straight line is approached the
log-log plot bends over to a gently curving line with a low slope as shown in Figure 2.5.6. In all pressure build-
up analyses where afterflow may be of importance the log-log data plot should be made before the straight line
is chosen on the semilog data plot, since it is often possible to draw a semi -log straight line through well-bore
storage dominated data. This phenomenon occurs because well-head shut-in does not correspond to sand-
face shut-in. As the sand-face flow does drop off to zero, the pressure increases rapidly to approach the
theoretically predicted level. The semilog data plot is steep and nearly linear during this period, and may be
analysed incorrectly seriously underestimating the formation permeability.

2.5.4. Determination of Reservoir Parameters

The basic method analysing pressure build-up data in an infinite-acting reservoir is the Horner plot of p
ws

versus ln((t
p
+ t)/t). It is important to remember that in this context "infinite-acting" refers to both the
production period before shut-in and to the ensuing closed-in period; thus it is a dual condition requiring that
neither the pressure disturbance from the initial production nor that from the rate change at shut-in reaches the
external boundary. It is recommended that the data points be plotted on ordinary graph paper as a plot of p
ws

versus ln( (t
p
+ t)/t) with bottom-hole shut-in pressure as ordinate and the natural log term as abscissa. The
data points influenced by well-bore storage are eliminated from consideration and a straight line is fitted to
those remaining by a linear least-squares regression. This process yields the slope, m , and the intercept, p*,
of equation (5.4).
Although it is not valid to extrapolate the straight line portion of the plot to very long shut-in times since the
term p
D
(t
D
) in the superposition is then no longer represented by the logarithmic approximation,
nevertheless, in an essentially infinite-acting reservoir, i.e. one with a short initial flow period, t
p
, it is often
assumed that the extrapolated pressure (intercept), p*, is synonymous with the initial pressure, p
i
, and the
mean drainage area pressure, p
-
. This is permissible provided the amount of fluid withdrawn from the reservoir
during the flow period is very small compared to the oil in place, i.e. negligible depletion has occurred. In this
situation then

p

= p
i
= p* . . . (5.13)

and the average drainage area pressure can be determined simply by extrapolating the linear portion of the
build-up.
The permeability-thickness product, kh , is calculated in the usual way from the measured slope, m , of the
fitted straight line using the formula:

kh =
q
s
B
4m
. . . . (5.14)

or, if field units are being used:

EPS Training
83
kh =
70.6q
s
B
m
(natural log) . (5.15)

kh =
162.6q
s
B
m
(log base 10) . (5.16)

Again if the net pay, h , is known the average permeability, k , of the area investigated can be calculated.
The superposition process showed that the ideal pressure behaviour (no well bore storage) after shut-in is
not influenced by the skin effect, S. Hence build-up data alone cannot be used to determine formation damage;
only the flowing pressure prior to shut-in is affected by the skin. For an infinite-acting reservoir the flowing
pressure just prior to shut-in is given by:

p
wf
(t = 0) = p
i

q
s
B
4kh

_
ln
kt
p
c
t
r
2
w
+ 0.80908 + 2S (5.17)

and, again for an infinite-acting system, the initial reservoir pressure, p
i
, can be replaced by the extrapolated
pressure, p*; hence equation (5.17) may be written:

p
wf
(t = 0) = p* + m

_
ln
kt
p
c
t
r
2
w
+ 0.80908 + 2S (5.18)

where
q
s
B
4kh
has been replaced by the measured slope of the build-up Horner plot, m . Solving equation
(5.18) for the skin factor, S , results in:

S =
1
2

_
p
wf
(t = 0) p*
m
ln
kt
p
c
t
r
2
w
0.80908 (5.19)

where the slope, m , is an intrinsically negative quantity.
The equivalent formulae for the skin factor when using field units are:

(a) natural log basis

S =
1
2

_
p
wf
(t = 0) p*
m
ln
kt
p
c
t
r
2
w
+ 7.43173 (5.20)

where m =
70.6q
s
B
kh


and (b) log base 10

S = 1.1513

]
1
1
1
p
wf
(t = 0) p*
m
log
10

kt
p
c
t
r
2
w
+ 3.2275 (5.21)

where m =
162.6q
s
B
kh


When semilog graph paper with a limited number of cycles is being employed it may be inconvenient to
extrapolate the straight line portion of the Horner plot sufficiently far to obtain p* directly. However it is
EPS Training
84
always possible to determine the pressure on the straight line 1 hour after shut-in; this is denoted p
ws
(t = 1)
or more simply p
1hr
.
The shut-in pressure, p
ws
, is given by:

p
ws
= p* + m log
t
p
+ t
t
. . . (5.22)

and hence:

p
ws
(t = 1) = p
1hr
= p* + m log (t
p
+ 1) . (5.23)

i.e.

p* = p
1hr
m log (t
p
+ 1) . . . (5.24)

Substituting this expression for p* into equation (5.21) gives:

S = 1.1513

]
1
1
1
p
wf
(t = 0) p
1hr
m
+ log
t
p
+ 1
t
p
log
k
c
t
r
2
w
+ 3.2275

. . . (5.25)

in which the term log ((t
p
+ 1)/t
p
) is frequently quite
negligible. This formula for the skin factor often
appears in the literature and the procedure for
finding p
1hr
is shown in Figure 2.5.7.

One advantage of a modern electronic pressure
transducer, with a high sampling rate, is that the last
flowing pressure, p
wf
(t = 0) , can be accurately
determined as illustrated in Figure 2.5.8; this is
important for the calculation of the skin. Note that
the clock time corresponding to t = 0 (the point at
which the valve actually closes) can also be
accurately bracketted. Precise estimates of pressure
and time at t = 0 are necessary for the log-log
diagnostic plots discussed in the next chapter. The
analysis of a buildup by the CRB method can be carried out even when the rate is varying during the
drawdown period as shown in Figure 2.5.8. The equivalent constant rate drawdown time is defined as:

t
p
=
Q
q
. . . . . (5.26)

Here Q is the cumulative volume produced over the whole flow period and q is the last, stabilised rate. This
approach should not be used when there is a strongly declining rate in the flowing period, as in a slug (rising
liquid level) test; in this case full superposition is necessary as described in Chapter 6.
Log
t + t
p

t
x
x
x
x
x
x
x
x
x
x
x
p*
p
1hr
slope m
0
Determination of p on the Horner Plot
1 hr
Fig 2.5.7
MTR
Straight
Line
t = 1 hr
S
p p
m
t
t
k
c r
wf hr p
p t w

+
+
+
L
N
M
M
O
Q
P
P
11513
1
3 2275
1
2
. . log log

p
ws
EPS Training
85
Determine and
very accurately
p ( t=0 t( t=0)
w
f
)
+
t( t=0)
p ( t=0)
wf

End of
Drawdown
Buildup
t
Stabilise flow-rate before shutin
q
Q = cumulative
volume
Flow-
Rate
t
Shutin
Afterflow
p = p p ( t=0)
BU ws wf
t = t t( t=0)
t =
p
Q
q
Test Precautions
Fig 2.5.8

In Figure 2.5.9 a typical chart from the original Amerada gauge is depicted and it can be seen that during the
flowing periods the bottom-hole pressure is actually increasing. This is the rising liquid level phenomenon
apparent in many old DSTs and Horner analysis of the final buildup is not really recommended because of the
implied rate variation. In 1976 the Hewlett-Packard company introduced the first quartz crystal pressure
transducer and this proved essential for the satisfactory conduct of well tests in the high permeability North
Sea basin. In Figure 2.5.10 a Horner plot of a pressure buildup in a Piper (Occidental) well is shown where the
total pressure change in the buildup (p
BU
) is less than 5 psi; it is immediately apparent why a high resolution
pressure gauge is necessary in this application.
Time
P
r
e
s
s
u
r
e
Flow period
Reservoir
Disturbance
Shut-in period
Reservoir
Recovery
Horner Plot
Large
m
Small
m
Same
p
r
p
ws
Log
t + t
p

t
Small Reservoir
Disturbance
Low flow-rate
Small viscosity
High permeability
Large Reservoir
Disturbance
High flow-rate
Viscous fluid
Low permeability
Permeability of Reservoir Rock from a DST
After Matthews and Russell
Large m
Small m
Scribed Tin Chart from Amerada Gauge
Fig 2.5.9






EPS Training
86
2.5.5. Peaceman Probe Radius

In Figure 2.5.2 the pressure redistribution in the reservoir during a buildup process has been generated
using the exponential integral solution and superposition; this diagram clearly illustrates how the buildup is a
relaxation of the pressure profile existing at the moment of shut-in back to equilibrium i.e. uniform pressure.
The buildup test measures the wellbore pressure, p
ws
, as a function of shut-in time, t , and it is of interest to
show how the buildup record can be used to infer the spatial pressure distribution present in the reservoir at
the moment of shut-in. Thus a transformation which takes p
ws
(t) and generates p
r
(t
p
,r), as shown in Figure
2.5.11, is required.
3424
3423
3422
p
ws
8 7 6 5 4
Horner Plot
Early Piper Well
(HP Gauge)
slope
m = 0.7465 psi
kh = 1.067
*
10 md.ft
S = 3.08
6
q = 11750 bbl/d
B = 1.28 = 0.75 cp
r = 0.362 ft = 0.237
c = 1.234
*
10 psi
s
w
t

-5 - 1
(psia)
Fig 2.5.10
l n
t t
t
p
+

3425
0
t
p
t
Pressure Build-Up in a Reservoir
t
1
t
2
t
3
t
4
t
5
p ( t , r )
r p p1
p ( t , r )
r p p 2
p ( t , r )
r p p 3
p( t , r )
r p p 4
p ( t , r )
r p p 5
p
r
r r
w
Reservoir pressure distribution
at moment of shut-i n, p(t)
r p
Peaceman Probe
Radius Concept
Fig 2.5.11
p p
w r
r r
w

The basis of the method can be examined for the case of a homogeneous system where the flowing
pressure at radius, r
d
, is predicted by the exponential integral expression:

p
wf,D( )
r
D
, t
pD
=
1
2
Ei

_
r
2
D
4 t
pD
. . . (5.27)

The shut-in pressure at time t
D
is given by:

p
ws,D( )
t
D
=
1
2
ln
t
p
+ t
t
. . . (5.28)

If the exponential integral can be replaced by the log approximation viz.:

p
wf,D( )
r
D
, t
pD
=
1
2
ln
4 t
pD
r
2
D
. . . (5.29)

then equating the pressures in (5.29) and (5.28) gives the correspondence result:


4 t
pD
r
2
D

t
p
+ t
t
i.e. r
d

4 k t
e
c
t
(5.30)

This calculation was first performed by Peaceman
(
9
)
who termed the equation for r
d
given above the
probe radius formu la.

9
Peaceman, D.W.:Interpretation of Well-Block Pressure in Numerical Simulation, JPT (June 1976),
183-194
EPS Training
87
The ability to generate the pressure distribution at fixed time, t
p
, allows the average pressure in the near
wellbore region to be computed. For example suppose a simulator block contains a well and it is desired to
relate the simulator block pressure to buildup surveys. If the simulator block has an area, A

, then the
equivalent radius, r

, is defined as:

r

=
A

. . . . (5.31)

The average pressure in this region can be obtained by integration of the reconstituted pressure profile i.e.

p

r
w
r

2 p
r
r dr
A

2.5.6. Transient Productivity Index, J
t


It is quite rare for the semi-steady-state
regime to be attained in an appraisal well test
and the drawdown period will usually fall into
the infinite-acting, transient period.
Supposing the major flow period is
terminated at time, t
p
, as illustrated in Figure
2.5.12 where the last flowing pressure is
denoted p
wf
(t
p
). The buildup, when plotted
on a Horner plot, will extrapolate to the initial
reservoir pressure, p
i
, as indicated by the
small vertical bar on the Fig 2.5.12 Cartesian
plot. It is often the practice to then define a
transient productivity index (P.I.) as:

J
t
=
q
s
p
i
p
wf
(t
p
)
. . . . (5.32)

It is apparent from the diagram that this quantity is highly time dependent especially when the flowing
time, t
p
, is short i.e. the flush production is high. In a well test the surface chokes will be set to maintain
the flow-rate at a value, q
s
, compatible with the test separator capacity. If the well is flowed for a long
time a semi-steady-state condition will be reached and the semi -steady-state P.I. of the form:

q
s
= J
sss

,
_
p

p
wf
. . . . (5.33a)

can be determined. In this case J
sss
will be described by an equation of the form:

J
sss
=
2kh
B

_
ln
r
e
r
w

3
4
+ S
. . (5.33b)

p
wf
p
i
Time, t
t
p2
t
p1
t
p1
t
p3
t
p3
t
p4
Transient Productivity Index, J
t
p (t )
wf p3
p
ws
or
J is strongly time dependent t
p
wf
J
q
p p t
t
s
i wf p

di
Fig 2.5.12
EPS Training
88
where r
e
is the equivalent circular radius of the well confining compartment. The important point is that
the transient P.I. defined by (5.32) is much higher than the stabilised value of (5.33). From the theory of
constant rate drawdown the transient P.I. is given by:

J
t
=
2kh
B

_
1
2
ln
4kt
c
t
r
2
w
+ S
. . . (5.34)

The difference between these two quite distinct forms of the productivity index is not properly
appreciated by many production engineers.
EPS Training
89

Fig 2.1.1 Drillstem Testing Assembly ............................................................................................................................43
Fig 2.1.2 Dual Flow Dual Shutin Test.............................................................................................................................45
Fig 2.1.3 Buildup Analysis on the Horner (Theis) Plot ...............................................................................................46
Fig 2.1.4 Physical Interpretation of the Skin Factor.....................................................................................................46
Fig 2.1.5 Use of the Horner Plot in Reservoir Monitoring ..........................................................................................47
Fig 2.1.6 Principle Flow Regimes in Constant Rate Drawdown..................................................................................47
Fig 2.1.7 Detection of Depletion in a Drillstem Test....................................................................................................48
Fig 2.1.8 Some Well Test Models ...................................................................................................................................48
Fig 2.1.9 Transient Heat Conduction in a Linear System............................................................................................49
Fig 2.2.1 Prototype Radial Reservoir of Fixed Thickness............................................................................................53
Fig 2.2.2 Transient Pressure Profiles in Radial Geometry............................................................................................56
Fig 2.2.3 Exponential Integral Function for a Single Well in an Infinite Reservoir..................................................59
Fig 2.2.4 Dimensionless Skin Factor, S..........................................................................................................................60
Fig 2.2.5 Ideal Constant Sandface Rate Drawdown .....................................................................................................61
Fig 2.2.6 Dimensionless Pressure Distributions in Radial Flow.................................................................................66
Fig 2.2.7 Exponential Integral Function .........................................................................................................................67
Fig 2.2.8 Depth of Investigation .....................................................................................................................................68
Fig 2.2.9 Well to Well Interference Test........................................................................................................................69
Fig 2.2.10 Radius of Drainage..........................................................................................................................................69
Fig 2.2.11 Theoretical Dimensionless Wellbore Pressure Response........................................................................71
Fig 2.2.12 Finite Wellbore Radius Solution...................................................................................................................71
Fig 2.2.13 Stabilised Pressure Distribution in SSS.......................................................................................................72
Fig 2.3.1 Diagrammatic Production and Pressure History for a Drawdown .............................................................72
Fig 2.3.2 Drawdown Semilog Plot ...................................................................................................................................73
Fig 2.4.1 Three Well Infinite System..............................................................................................................................76
Fig 2.4.2 Two-Rate Schedule ...........................................................................................................................................77
Fig 2.4.3 Superposition of Pressure Changes ...............................................................................................................78
Fig 2.5.1 Schematic Flow-Rate and Pressure Behaviour for an Ideal Buildup .........................................................78
Fig 2.5.2 Dimensionless Buildup Pressure Distributions............................................................................................80
Fig 2.5.3 Dimensionless Buildup Semilog Graph..........................................................................................................81
Fig 2.5.5 Effect of Wellbore Storage on a Buildup.......................................................................................................81
Fig 2.5.6 Log-Log Diagnostic Plot for a Buildup..........................................................................................................82
Fig 2.5.7 Procedure for Finding the MTR Pressure at 1 Hour ....................................................................................84
Fig 2.5.8 Test Precautions................................................................................................................................................84
Fig 2.5.9 Scribed Tin Chart from an Amerada Gauge...................................................................................................85
Fig 2.5.10 Horner Plot from an Early Piper Well............................................................................................................85
Fig 2.5.11 Peaceman Probe Radius Concept .................................................................................................................86
Fig 2.5.12 Transient Productivity Index, J
t
.....................................................................................................................87
EPS Training
90

Fig 2.1.1...ptaintf1...............................................................................................................................................................43
Fig 2.1.2...ptaintf2...............................................................................................................................................................45
Fig 2.1.3...ptaintf3...............................................................................................................................................................46
Fig 2.1.4...ptaintf4...............................................................................................................................................................46
Fig 2.1.5...ptaintf5...............................................................................................................................................................47
Fig 2.1.6...ptaintf6...............................................................................................................................................................47
Fig 2.1.7...ptaintf7...............................................................................................................................................................48
Fig 2.1.8...ptaintf8...............................................................................................................................................................48
Fig 2.1.9...ptaintf9...............................................................................................................................................................49
Fig 2.2.1...ptabfi1................................................................................................................................................................53
Fig 2.2.2...ptabfi2................................................................................................................................................................56
Fig 2.2.3...ptabfi3................................................................................................................................................................59
Fig 2.2.4...ptabfi7................................................................................................................................................................60
Fig 2.2.5...ptabfi8................................................................................................................................................................61
Fig 2.2.6...ptabfi4................................................................................................................................................................66
Fig 2.2.7...ptabfi9................................................................................................................................................................67
Fig 2.2.8...ptabfi5................................................................................................................................................................68
Fig 2.2.9...ptabfi10..............................................................................................................................................................69
Fig 2.2.10...ptabfi11............................................................................................................................................................69
Fig 2.2.11...ptabfi6..............................................................................................................................................................71
Fig 2.2.12...ptabfi12............................................................................................................................................................71
Fig 2.2.13...ptabfi13............................................................................................................................................................72
Fig 2.3.1...ptapdtf1..............................................................................................................................................................72
Fig 2.3.2...ptapdtf2..............................................................................................................................................................73
Fig 2.4.1...ptaposf1.............................................................................................................................................................76
Fig 2.4.2...ptaposf2.............................................................................................................................................................77
Fig 2.4.3...ptaposf3.............................................................................................................................................................78
Fig 2.5.1...ptapbtf1..............................................................................................................................................................78
Fig 2.5.2...ptapbtf2..............................................................................................................................................................80
Fig 2.5.3...ptapbtf3..............................................................................................................................................................81
Fig 2.5.5...ptapbtf5..............................................................................................................................................................81
Fig 2.5.6...ptapbtf6..............................................................................................................................................................82
Fig 2.5.7...ptabfi14..............................................................................................................................................................84
Fig 2.5.8...ptabfi15..............................................................................................................................................................84
Fig 2.5.9...ptabfi16..............................................................................................................................................................85
Fig 2.5.10...ptabfi17............................................................................................................................................................85
Fig 2.5.11ptapbtf8...........................................................................................................................................................86
Fig 2.5.12ptapbtf9...........................................................................................................................................................87