Control Systems - Notes

Dr.Y.NARASIMHA MURTHY Ph.D yayavaram@yahoo.
com
CONTROL SYSTEMS
INTRODUCTION : A control system is one which can control any quantity of interest in a machine, mechanism or other equipment in order to achieve the desired performance or output.(or) A control system is an interconnection of components connected or related in such a manner as to command, direct, or regulate itself or another system. For example consider, the driving system of an automobile.
Speed of the automobile is a function of the position of its accelerator. The desired speed can be maintained (or a desired change in speed can be achieved) by controlling pressure on the accelerator pedal. This automobile driving system (accelerator, carburetor and engine-vehicle) constitutes a control system. Control systems find numerous and widespread applications from everyday to extraordinary in science, industry, and home. Here are a few examples: (a) Home heating and air-conditioning systems controlled by a thermostat (b) The cruise (speed) control of an automobile (c) Manual control (i) Opening or closing of a window for regulating air temperature or air quality (ii) Activation of a light switch to regulate the illumination in a room (iii) Human controlling the speed of an automobile by regulating the gas supply to the engine (d) Automatic traffic control (signal) system at roadway intersections (e) Control system which automatically turns on a room lamp at night, and turns it off in Day light The general block diagram of a control system is shown below.
.
Fig.1 .Block diagram of a control system.
Dr.Y.NARASIMHA MURTHY Ph.D yayavaram@yahoo.com
The above method of representation of a control system is known as block diagram representation where in each block represents an element, a plant, mechanism, device etc.,
whose inner details are not indicated. Each block has an input and output signal which are linked by a relationship characterizing the block. It may be noted that the signal flow through the block is unidirectional Basic Control System components : The basic control system components are objectives i.e inputs or actuating signals to the system and the Output signals or controlled variables etc.The control system will control the outputs in accordance with the input signals.The relation beteen these components is shown in the block diagram.
The components of the control system changes as we move from openloop control system to closed loop control systems. In a closed loop control system ,the feedback control network play an important role in getting the correct output.
The general block diagram of a control system with feed back is shown below. The error detector compares a signal obtained through feedback elements, which is a function of the output response, with the reference input. Any difference between these two signals gives an error or actuating signal, which actuates the control elements. The control elements in turn alter the conditions in the plant in such a manner as to reduce the original error.
Fig.2 .General block diagram of an automatic control system. Types of control systems : There are basically two types of control systems (i) the open loop system and the (ii) closed loop system. They can both be represented by block diagrams. A block diagram uses blocks to represent processes, while arrows are used to connect different input, process and output parts. Open loop Control System : Asystem which do not possess any feed back network ,and contains only the input and output relationship is known as a open loop control system .
Examples of the open loop control systems are washing machines, light switches, gas ovens, burglar alarm system etc. The drawback of an open loop control system is that it is incapable of making automatic adjustments. Even when the magnitude of the output is too big or too small, the system cant make the necessary adjustments. For this reason, an open loop control system is not suitable for use as a complex control system.
3
Closed loop control system : A closed loop system is one which uses a feed back control between input and output. A closed loop control system compares the output with the expected result or command status, then it takes appropriate control actions to adjust the input signal. Therefore, a closed loop system is always equipped with a sensor, which is used to monitor the output and compare it with the expected result.
The output signal is fed back to the input to produce a new output. A well-designed feedback system can often increase the accuracy of the output. Examples for closed loop systems are air conditioners, refrigerators, automatic rice cookers,
automatic ticketing machines, etc. For example An air conditioner, uses a thermostat to detect the temperature and control the operation of its electrical parts to keep the room temperature at a preset constant. One advantage of using the closed loop control system is that it is able to adjust its output automatically by feeding the output signal back to the input. When the load changes, the error signals generated by the system will adjust the output suitably. The limitation of a closed loop control systems is they are generally more complicated and thus also more more expensive to design. Linear versus Nonlinear Control Systems : Linear feedback control systems are idealized models fabricated by the analyst purely for the simplicity of analysis and design When the magnitudes of signals in a control system are limited to ranges in which system components exhibit linear characteristics (i.e., the principle of superposition applies), the system is essentially linear. But when the magnitudes of signals are extended beyond the range of the linear operation, depending on the severity of the nonlinearity, the system should no longer be considered linear. For instance, amplifiers used in control systems often exhibit a saturation effect when their input
4
signals become large; the magnetic field of a motor usually has saturation properties. Other common nonlinear effects found in control systems are the backlash or dead play between coupled gear members, nonlinear spring characteristics, nonlinear friction force or torque between moving members, and so on. Quite often, nonlinear characteristics are intentionally introduced in a control system to improve its performance or provide more effective control. Also the analysis of linear systems is easy and lot of mathematical solutions are available for their simplification. Nonlinear systems, on the other hand, are usually difficult to treat mathematically, and there are no general methods available for solving a wide class of nonlinear systems. In practice , first a linear-system is modeled by neglecting the nonlinearities of the system and the designed controller is then applied to the nonlinear system model for evaluation or redesign by computer simulation. Distinguish between Openloop and Closed loop control systems
Time-Invariant control Systems : When the parameters of a control system do not change with respect to time during the
operation of the system, the system is called a time-invariant system. In practice, most physical systems contain elements that drift or vary with time. For example, the winding resistance of an electric motor will vary when the motor is first being excited and its temperature is rising. Another example of a time-varying system is a guided-missile control system in which the mass
of the missile decreases as the fuel on board is being consumed during flight. Although a timevarying system without nonlinearity is still a linear system, the analysis and design of this class of systems are usually much more complex than that of the linear time-invariant systems.
Continuous and Discrete Data Control Systems : A continuous-data system is one in which the signals at various parts of the system are all functions of the continuous time variable t. The signals in continuous-data systems may be further classified as ac or dc. In control systems the ac control system, means that the signals in the system are modulated by some form of modulation scheme. A dc control system, on the other hand, simply implies that the signals are unmodulated, but they are still ac signals according to the conventional definition. The schematic diagram of a closed loop dc control system is shown below. Typical waveforms of the signals in responseto a step-function input are shown in the figure. Typical components of a dc control system are potentiometers, dc amplifiers, dc motors, dc tachometers, and so on.
In ac control systems , the signals are modulated i.e the information is transmitted by an ac carrier signal. Here the output controlled variable behaves similarly to that of the dc system. In this case, the modulated signals are demodulated by the low-pass characteristics of the ac motor. Ac control systems are used extensively in aircraft and missile control systems in which noise
6
and disturbance often create problems. By using modulated ac control systems with carrier frequencies of 400 Hz or higher, the system will be less susceptible to low-frequency noise. Typical components of an ac control system are synchros, ac amplifiers, ac motors, gyroscopes, accelerometers etc. Discrete Data Control System If the signal is not continuously varying with time but it is in the form of pulses then the control system is called Discrete Data Control System.If the signal is in the form of pulse data, then the system is called Sampled Data Control System. Here the information supplied intermittently at specific instants of time. This has the advantage of Time sharing system. On the other hand, if the signal is in the form of digital code, the system is called Digital Coded System. Here use of Digital computers, micro processors or microcontrollers are made use of such systems and are analyzed by the Z- transform theory.
Block Diagrammatic Representation :

It is a representation of the control system giving the inter-relation between the transfer function of various components. The block diagram is obtained after obtaining the differential equation & Transfer function of all components of a control system. The arrow head pointing towards the block indicates the i/p & pointing away from the block indicates the o/p. Suppose G(S) is the Transfer function then G(S) = C(S) / R(S)
After obtaining the block diagram for each & every component, all blocks are combined to get a complete representation. It is then reduced to a simple form with the help of block diagram algebra. Basic elements of a block diagram Blocks Transfer functions of elements inside the blocks Summing points Take off points Arrow
A control system may consist of a number of components. A block diagram of a system is a pictorial representation of the functions performed by each component and of the flow of signals. The elements of a block diagram are block, branch point and summing point. Block : In a block diagram all system variables are linked to each other through functional blocks. The functional block or simply block is a symbol for the mathematical operation on the input signal to the block that produces the output.
Summing point : The blocks are used to identify many types of mathematical operations, like addition and subtraction and represented by a circle, called a summing point. As shown belowdiagram a summing point may have one or several inputs. Each input has its own appropriate plus or minus sign. A summing point has only one output and is equal to the algebraic sum of the inputs
A takeoff point is used to allow a signal to be used by more than one block or summing point Arrow associated with each branch to indicate the direction of flow of signal Advantages of Block Diagram Representation : It is always easy to construct the block diagram even for a complicated system Function of individual element can be visualized Individual & Overall performance can be studied Over all transfer function can be calculated easily
Limitations of a Block Diagram Representation No information can be obtained about the physical construction Source of energy is not shown
Block diagram reduction technique: Because of the simplicity and versatility, the block diagrams are often used by control engineers to describe all types of systems. A block diagram can be used simply to represent the composition and interconnection of a system. Also, it can be used, together with transfer functions, to represent the cause-and-effect relationships throughout the system. Transfer Function is defined as the relationship between an input signal and an output signal to a device. Procedure to solve Block Diagram Reduction s : Step 1: Reduce the blocks connected in series Step 2: Reduce the blocks connected in parallel Step 3: Reduce the minor feedback loops Step 4: Try to shift take off points towards right and Summing point towards left Step 5: Repeat steps 1 to 4 till simple form is obtained Step 6: Obtain the Transfer Function of Overall System Block diagram rules (1) Blocks in Cascade [Series] : When two blocks are connected in series ,their resultant transfer function is the product of two individual transfer functions.
(2) Combining blocks in Parallel: When two blocks are connected parallel as shown below ,the resultant transfer function is equal to the algebraic sum (or difference) of the two transfer functions.This is shown in the diagram below.
(3) Eliminating a feed back loop:The following diagram shows how to eliminate the feed back loop in the resultant control system
(4) Moving a take-off point beyond a block: The effect of moving the takeoff point beyond a block is shown below.
(5) Moving a Take-off point ahead of a block: The effect of moving the takeoff point ahead of a block is shown below.
10
Applications of the control systems : There are various applications of control systems which include biological propulsion; locomotion; robotics; material handling; biomedical, surgical, and endoscopic ; aeronautics; marine and the defense and space industries. There are also many household and industrial application examples of the control systems, such as washing machine, air conditioner, security alarm system and automatic ticket selling machine, etc. (i) Washing machine : The most commonly used house hold application is the washing machine.It comes under
automatic control system ,where the machine automatically starts to pour water, add washing powder, spin and wash clothes, discharge wastewater, etc. After the completion of all the procedures, the washing machine will stop the operation. However, this kind of machine only operates according to the preset time to complete the
whole washing process. It ignores the cleanness of the clothes and does not generate feedback. Therefore, this kind of washing machine is of open loop control system. (ii). Air conditioner The air conditioner is used to automatically control the temperature of the room.In the air conditioner the coolant circulated in the machine will absorb heat indoor, then it will be
transported from the vaporization device to cooling device. The hot air is then blown to outdoor by a fan. There is an adjustable temperature device equipped in the air conditioner for the users to adjust the extent of cooling. When the temperature of the cool air is lower than the preset one, the controller of the air conditioner will stop the operation of the compressor to cease the circulation of the coolant. The temperature sensor installed near the vaporization device will continuously measure the indoor temperature, and send the results to the controller for further processing.This operation will come under closed loop control system.Thesimple block diagram of air conditioner system is shown below.
11
Feed back Control System : The feed back control system is represented by the following block diagram .In the diagram feed back signal is denoted by B(S) and the output is C(S).The input function is denoted by R(S).
The open loop gain of the system is G(S) and the feed back loop gain H(S). Then the feed back signal b(s) is given by B(S) = H(S). C(S) Transfer function : The input- output relationship in a linear time invariant system is given by the transfer function.For a time invariant system it is defined as the ratio of Laplace transform of the out to the Lapalce transform of the input The important features of the transfer functions are, The transfer function of a system is the mathematical model expressing the differential equation that relates the output to input of the system. The transfer function is the property of a system independent of magnitude and the nature of the input . The transfer function includes the transfer functions of the individual elements. But at the same time, it does not provide any information regarding physical structure of the system If the transfer function of the system is known, the output response can be studied for various types of inputs to understand the nature of the system It is applicable to Linear Time Invariant system. It is assumed that initial conditions are zero. It is independent of i/p excitation. It is used to obtain systems o/p response. If the transfer function is unknown, it may be found out experimentally by applying known inputs to the device and studying the output of the system
12
From the above block diagram G(S) = C(S) / E(S) & E(S) = R(S) B(S) So, C(S) = G(S) .E(S) = G(S)[ R(S)- B(S) = G(S) [ R(S) H(S).C(S) Therefore
This is the transfer function of the closed loop control system
Properties of Systems : For any control system to understand its performance the following properties are very important. (i).Linearity : A system is said to be linear if it follows both the law of addtivity and law of homogeneity. The system which do not follow the law of homogeneity and additivity is called a non-linear system. If input x1(t) produces response y1(t) and input x2(t) produces response y2(t) then the scaled and summed input a1x1(t) +b1x2(t) produces the scaled and summed response a1y1(t) +b1y2(t) where a1 and a2 are real scalars. It follows that this can be extended to an arbitrary number of terms, and so for real numbers . (ii) Time Invariance : A system with input x(t) and output y(t) is time-invariant if x(t- t0) is creates output y ( t t0) for all inputs x and shifts t0. (iii). Causality : A system is causal, if the output y(t) at time t is not a function of future inputs and it depends only on the present and past inputs . All analog systems are causal and all memeoryless systems are causal . If the system is causal, then this implies h(t) = 0, t < 0. Alternatively, h[n]=0, n < 0. (iv).Stability : A system is said to be a stable if for every bounded-input there exists a bounded output . Transfer Function: For a open loop control system shown below the transfer function is the ratio of Laplace transform of the out-put to the Laplace transform of the input.
13
The Laplace transform of the Input is R(S) and the Laplace transform of the output is C(S) . So,the Transfer function of the system is G(S) = C(S) / R(S) Example : Find the transfer function of the following RC circuit
By definition ,the transfer function is G(S) =
14
The Laplace transformed Network is shown above.From the circuit we can write that
Poles and Zeros : In the transfer function of a control system both numerator and denominator will be polynomials. If these numerator and denominator are solved , the roots of the numerator are called Zeros and the roots of the denominator are called the Poles. These poles of the transfer function decides the stability of the control system. The transfer function provides a basis for determining important system response characteristics without solving the complete differential equation. As defined, the transfer function is given by the following expression with variable s = + j,
It is always easy to factor the polynomials in the numerator and denominator, and to write
15
the transfer function in terms of those factors .then the above transfer function can be written as
where the numerator and denominator polynomials, N(s) and D(s), have real coefficients defined by the systems differential equation and K = bm/an. As written in the above equation the Zi s are the roots of the equation N(s) = 0, and are
defined to be the system Zeros, and the pi s are the roots of the equation D(s) = 0, and are defined to be the system poles. All of the coefficients of polynomials N(s) and D(s) are real, therefore the poles and zeros must be either purely real, or appear in complex conjugate pairs. The stability of a linear system may be determined directly from its transfer function. An nth order linear system is asymptotically stable only if all of the components in the homogeneous response from a finite set of initial conditions decay to zero as time increases, or
where the pi are the system poles. In a stable system all components of the homogeneous response must decay to zero as time increases. If any pole has a positive real part there is a component in the output that increases without bound, causing the system to be unstable.
16
Example : A linear system is described by the differential equation
Find the system poles and zeros. Solution: From the differential equation the transfer function is
So,the system has a single real zero at s = 1/2, and a pair of real poles at s = 3 and s = 2. SIMULATION DIAGRAMS: The simulation diagram is similar to the diagram used to represent the system on an analog computer.The basic elements used are ideal integrators, ideal amplifiers, and ideal summers, shown in below diagram. Additional elements such as multipliers and dividers may be used for nonlinear systems.
17
To obtain the simulation diagram ,the following steps are to be followed. 1. Start with differential equation. 2. On the left side of the equation put the highest-order derivative of the dependent variable. A first-order or higher-order derivative of the input may appear in the equation. In this case the highest-order derivative of the input is also placed on the left side of the equation. All other terms are put on the right side. 3. Start the diagram by assuming that the signal, represented by the terms on the left side of the equation, is available. Then integrate it as many times as needed to obtain all the lowerorder derivatives. It may be necessary to add a summer in the simulation diagram to obtain the dependent variable explicitly. 4. Complete the diagram by feeding back the approximate outputs of the integrators to a summer to generate the original signal of step 2.Include the input function if it is required. Example: Draw the simulation diagram for the series RLCcircuit of below figure in which the output is the voltage across the capacitor. SIGNAL FLOW GRAPHS(SFG) : The block diagram method is a useful tool for simplifying the representation of a control system. But when there are more than two feed back loops and if there exists inter-coupling between feedback loops, and when a system has more than one input and one output, the block diagram approach is very complex. Hence an alternate method is proposed by S.J. Mason. This method is called signal flow graphs. In these graphs each node
18
represents a system variable & each branch connected between two nodes acts as Signal Multiplier. The direction of signal flow is indicated by an arrow. A signal flow graph is a diagram that represents a set of simultaneous equations. It consists of a graph in which nodes are connected by directed branches. The nodes represent each of the system variables. A branch connected between two nodes acts as a one-way signal multiplier: the direction of signal flow is indicated by an arrow placed on the branch, and the multiplication factor (transmittance or transfer function) is indicated by a letter placed near the arrow.
So,in the figure above , the branch transmits the signal x1 from left to right and multiplies it by the quantity a in the process. The quantity a is the transmittance, or transfer function. Flow-Graph Definitions : A node performs two functions: Addition of the signals on all incoming branches and Transmission of the total node signal (the sum of all incoming signals) to all outgoing branches
There are three types of nodes .They are Source nodes , Sink nodes and Mixed nodes Source nodes (independent nodes) : These represent independent variables and have only outgoing branches. In Fig. 5.21, nodes u and v are source nodes. Sink nodes (dependent nodes): These represent dependent variables and have only incoming branches. In Fig (a), nodes x and y are sink nodes. Mixed nodes (general nodes): These have both incoming and outgoing branches. In Fig. (a), node w is a mixed node. A mixed node may be treated as a sink node by adding an out going branch of unity transmittance, as shown in Fig (b), for the equation x = au +bv and w = cx = cau + cbv
19
Fig(a)
Fig (b)
A path is any connected sequence of branches whose arrows are in the same direction and A forward path between two nodes is one that follows the arrows of successive branches and in which a node appears only once. In Fig.(a) the path uwx is a forward path between the nodes u and x. Flow-Graph Algebra : The following rules are useful for simplifying a signal flow graph: Series paths (cascade nodes). Series paths can be combined into a single path by multiplying the transmittances as shown in Fig ( A ). Path gain. The product of the transmittances in a series path. Parallel paths. Parallel paths can be combined by adding the transmittances as shown in Fig(B). Node absorption. A node representing a variable other than a source or sink can be eliminated as shown in Fig (C). Feedback loop. Aclosed path that starts at a node and ends at the same node. Loop gain. The product of the transmittances of a feedback loop. These results are shown diagrammatically in the following figures (A) ,(B) and C) where the original diagram and equivalent diagrams are shown.
20
Masons gain formula: The relationship between an input variable and an output variable of a signal flow graphis given by the net gain between input and output nodes and is known as overall gain ofthe system. Masons gain formula is used to obtain the over all gain (transfer function) of signal flow graphs. According to Masons gain formula Gain is given by
Where, Pk is gain of k th forward path and is determinant of graph. Here the is given by = 1-(sum of all individual loop gains)+(sum of gain products of all possible combinations of two non touching loops sum of gain products of all possible combination of three non touching loops) k is cofactor of kth forward path determinant of graph with loops touching k th forward path. It is obtained from by removing the loops touching the path Pk. Finding transfer function from the system flow graphs is explained below by example . Example1 : Obtain the transfer function of the system whose signal flow graph is shown below.
21
There are two forward paths: One is Gain of path 1 : P1=G1 and the other is Gain of path 2: P2=G2 There are four loops with loop gains : L1=-G1G3, L2=G1G4, L3= -G2G3, L4= G2G4 There are no non-touching loops. = 1+G1G3-G1G4+G2G3-G2G4 Forward paths 1 and 2 touch all the loops. Therefore, 1= 1, 2= 1 So,the transfer function T is given by
22
Example 2 : Obtain the transfer function of C(s) /R(s) of the system whose signal flow graph shown below.
From the system flow graph it is clear that There is one forward path, whose gain is: P1=G1G2G3 There are three loops with loop gains: L1=-G1G2H1, L2=G2G3H2, L3= -G1G2G3 There are no non-touching loops: = 1-G1G2H1+G2G3H2+G1G2G3 Forward path 1 touches all the loops. Therefore, 1= 1. The transfer function T is given by
System Stability: The study of stability of a control system is very important to understand the performance . This means that the system must be stable at all times during operation. Stability may be used to define the usefulness of the system. Stability studies include absolute & relative stability. Absolute stability is the quality of stable or unstable performance. Relative Stability is the quantitative study of stability.
23
The stability study is based on the properties of the Transfer Function. In the analysis, the characteristic equation is very important ,which describe the transient response of the system. From the roots of the characteristic equation, following conclusions about the stability can be drawn. (1) When all the roots of the characteristic equation lie in the left half of the S-plane, the system response due to initial condition will decrease to zero at time Thus the system will be termed as a stable system. (2) When one or more roots lie on the imaginary axis & there are no roots on the RHS of Splane, the response will be oscillatory without damping. Such a system will be termed as critically stable. (3) When one or more roots lie on the RHS of S-plane, the response will exponentially increase in magnitude and there by the system will be Unstable. Stability Definitions : A system is stable, if its o/p is bounded for any bounded i/p . or A system is stable, if its response to a bounded disturbing signal vanishes ultimately as time t approaches infinity. A system is un stable, if its response to a bounded disturbing signal results in an o/p of infinite amplitude or an Oscillatory signal. If the o/p response to a bounded i/p signal results in constant amplitude or constant amplitude oscillations, then the system may be stable or unstable under some limited constraints. Such a system is called Limitedly Stable system. If a system response is stable for a limited range of variation of its parameters, it is called Conditionally Stable System. If a system response is stable for all variation of its parameters, it is called Absolutely Stable system.
Routh-Hurwitz Stability Criterion : This criterion is derived from the theory of equations
and is an algebraic method to determine the number of roots of a given equation with positive real part. The Routh-Hurwitz criterion is a method of finding whether a linear system is stable or not by examining the locations of the roots of the characteristic equation of the system. In fact, the
24
method determines only if there are roots that lie outside of the left half plane; it does not actually compute the roots. To determine whether this system is stable or not, check the following conditions Two necessary but not sufficient conditions that all the roots have negative real parts are a) All the polynomial coefficients must have the same sign. b) All the polynomial coefficients must be nonzero. A sufficient condition for a system to be stable is that each & every term of the column of the Routh array must be positive or should have the same sign. Routh array can be obtained as follows Consider the Characteristic equation of the form,
Similarly rest of the elements, can be evaluated. The limitations of the Routh-Hurwitz stability criteria are (1) It is valid only if the Characteristic equation is algebraic. (2) If any co-efficient of the Characteristic equation is complex or contains power of e this criterion can not be applied. (3) It gives information about how many roots are lying in the RHS of S-plane; values of the roots are not available. Also it cannot distinguish between real & complex roots.
25
Special cases in Routh-Hurwitz criteria : (1) When the 1st term in a row is zero, but all other terms is non-zeroes then substitute a small positive number for zero & proceed to evaluate the rest of the elements. When the 1 st column term is zero, it means that there is an imaginary root. (2) All zero row: In the case, write auxiliary equation from preceding row, differentiate this equation & substitute all zero row by the co-efficient obtained by differentiating the auxiliary equation. This case occurs when the roots are in pairs. The system is said to be limitedly stable. Application of Rouths Criteria : Rouths criterion can be applied to determine range of certain parameters of a system to ensure stability. For example, it is usually of interest to find the range of the open loop gain K for closed loop stability. Example 1 : Find the stability of a system whose characteristic equation is given below.
From the above table it is clear that the no. of sign changes in the 1st column = zero. No roots are lying in the RHS of S-plane. So, the given System is Absolutely Stable.
26
Example 2: Find the stability of a system whose characteristic equation is given below .
From the above table it is clear that the no. of sign changes in the 1st column = 2 and two roots
are lying in the RHS of S-plane. So , the given System is unstable ROOT LOCUS : Root locus is the plot of the loci of the root of the complementary equation when one or more parameters of the open-loop Transfer function are varied, mostly the only one variable available is the gain K The negative gain has no physical significance hence varying K from 0 to , the plot is obtained called the Root Locus Point. Root locus gives the complete dynamic response of the system. It provides a measure of sensitivity of roots to the variation in the parameter being considered. It is applied for single as well as multiple loop system Rules for the Construction of Root Locus : (1) The root locus is symmetrical about the real axis. (2) The no. of branches terminating on equals the no. of open-loop pole-zeroes.
27
(3) Each branch of the root locus originates from an open-loop pole at K = 0 & terminates at open-loop zero corresponding to K = . (4) A point on the real axis lies on the locus, if the no. of open-loop poles & zeroes on the real axis to the right of this point is odd. (5) The root locus branches that tend to , do so along the straight line. Asymptotes making angle with the real axis is given by
Where, n=1,3,5, P is the number of poles and z is the number of zeros (6) The asymptotes cross the real axis at a point known as Centroid (7) The break away or the break in points [Saddle points] of the root locus are determined from the roots of the equation dk /ds = 0.
(8) The intersection of the root locus branches with the imaginary axis can be determined by the use of Routh-Hurwitz criteria or by putting s= j in the characteristic equation & equating the real part and imaginary to zero. To solve for and K i.e., the value of is intersection point on the imaginary axis & K is the value of gain at the intersection point. 9) The angle of departure from a complex open-loop pole d is given by d = 1800 + GH Nyquist Criteria: A stability test for time invariant linear systems can also be derived in the frequency domain. It is known as Nyquist stability criterion. It is based on the complex analysis result known as Cauchys principle of argument. The Nyquist stability criterion relates the location of the roots of the characteristic equation to the open-loop frequency response of the system. In this, the computation of closed-loop poles is not necessary to determine the stability of the system and the stability study can be carried out
28
graphically from the open-loop frequency response. Therefore experimentally determined openloop frequency response can be used directly for the study of stability. When the feedback path is closed. The Nyquist criterion provides the information on absolute and relative stability of the system.
Let us suppose that the system transfer function is a complex function. By applying Cauchys principle of argument to the open-loop system transfer function, we will get information about stability of the closed-loop system transfer function and arrive at the Nyquist stability criterion The importance of Nyquist stability lies in the fact that it can also be used to determine the relative degree of system stability by producing the so-called phase and gain stability margins. These stability margins are needed for frequency domain controller design techniques The Nyquist plot is a polar plot of the function D(s) = 1 = G(s).H(s)
29
The Nyquist criterion states that the number of unstable closed-loop poles is equal to the number of unstable open-loop poles plus the number of encirclements of the origin of the Nyquist plot of the complex function D(s). Continuous Time Feedback Control Systems : If the signals in all parts of a control system are continuous functions of time, the system is classified as continuous time feedback control system. Typically all control signals are of low frequency and if these signals are un modulated, the system is known as a d.c. control system. These systems use potentiometers as error detectors, d.c amplifiers to amplify the error signal, d.c. servo motor as actuating device and d.c tachometers or potentiometers as feedback elements. If the control signal is modulated by an a.c carrier wave, the resulting system is usually referred to as an a.c control system. These systems frequently use synchros as error detectors and modulators of error signal, a.c amplifiers to amplify the error signal and a.c servo motors as actuators. These motors also serve as demodulators and produce an un modulated output signal. Discrete Data Feedback Control Systems Discrete data control systems are those systems in which at one or more pans of the feedback control system, the signal is in the form of pulses. Usually, the error in such system is sampled at uniform rate and the resulting pulses are fed to the control system. In most sampled data control systems, the signal is reconstructed as a continuous signal, using a device called 'hold device'. Holds of different orders are employed, but the most common hold device is a zero order hold. It holds the signal value constant, at a value equal to the amplitude of the input time function at that sampling instant, until the next sampling instant .These systems are also known as sampled data control systems.
30
Fig : Discrete Data Feedback Control Systems Discreet data control systems, in which a digital computer is used as one of the elements, are known as digital control systems. The input and output to the digital computer must be binary numbers and hence these systems require the use of digital to analog and analog to digital converters
Time response analysis : It is an equation or a plot that describes the behavior of a system and gives information about it with respect to time response specification as overshooting, settling time, peak time, rise time and steady state error. Time response is formed by the transient response and the steady state response. Time response = Transient response + Steady state response.
Transient time response or Natural response describes the behavior of the system in its first short time until arrives the steady state value. If the input is step function then the output or the response is called step time response and if the input is ramp, the response is called ramp time response .. etc. Transient Response: The transient response is defined as the part of the time response that goes to zero as time becomes very large. Thus yt(t) has the property Lim y(t) = 0 t --> The time required to achieve the final value is called transient period. The transient response may be exponential or oscillatory in nature. Output response consists of the sum of forced response (form the input) and natural response (from the nature of the system).The transient response is the change in output response from the beginning of the response to the final state of the response and the steady state response is the output response as time is approaching infinity (or no more changes at the output). The behavior of a system in transient state is shown below.
31
Steady State Response: The steady state response is the part of the total response that remains after the transient has died out. For a position control system, the steady state response when compared to with the desired reference position gives an indication of the final accuracy of the system. If the steady state response of the output does not agree with the desired reference exactly, the system is said to have steady state error. Response to a Unit Step Input First Order
Consider a feedback system with G)s) = 1/s as shown below
The closed loop transfer function of the system is given by
32
For a unit step input R (s) = 1 / s and the output is given by
Inverse Laplace transformation yields

The plot of c(t) Vs t is shown below
The response is an exponentially increasing function and it approaches a value of unity as

t --- >
At t = the response reaches a value, which is 63.2 percent of the steady value. This time, is known as the time constant of the system. One of the important characteristics about the system is its speed of response or how fast the response is approaching the final value. The time constant is indicative of this measure and the speed of response is inversely proportional to the time constant of the system.Another important characteristic of the system is the error between the desired value and the actual value under steady state conditions. This quantity is known as the steady state error of the - system and is denoted by ess.
The error E(s) for a unity feedback system is given by
33
For the system under consideration G(s) = 1 / s and R(s) = 1 /s
Therefore
As t ~ e (t) ~ 0 . Thus the output of the first order system approaches the reference input, which is the desired output, without any error. In other words, we say a first order system tracks the step input without any steady state error. Response to a Unit Ramp Input :
To study the response of a unit ramp let us consider a feedback system with G)s) = 1/s as shown below
The response of the system for which , R(s) = 1 / s2 is given by
The time response is obtained by taking inverse Laplace transform of above equation
34
Differentiating the above equation we get
This is the response of the system to a step input. Thus no additional information about the speed of response is obtained by considering a ramp input.So, no additional information about the speed of response is obtained by considering a ramp input. But the effect on the steady state error is given by
Thus the steady state error is equal to the time constant of the system. The first order system, therefore, can not track the ramp input without a finite steady state error. If the time constant is reduced not only the speed of response increases but also the steady state error for ramp input decreases. Hence the ramp input is important to the extent that it produces a finite steady state error. The response of a first order system for unit ramp input is shown below.
35
Response to a Unit Step Input - Second Order System
Let us consider a type 1, second order system as shown in Fig.below. Since G(s) has one pole at the origin, it is a type one system.
The closed loop transfer function is give by,
The transient response of any system depends on the poles of the transfer function T(s). The roots of the denominator polynomial in s of T(s) are the poles of the transfer function. Thus the denominator polynomial of T(s), given by D(s) = s2 + S + K
36
is known as the characteristic polynomial of the system and D(s) = 0 is known as the characteristic equation of the system. The above Eqn. is normally put in standard from, given by,
The poles of T( s), or, the roots of the characteristic equation S2 + 2 n s + n 2 = 0 are given by,
Where
is known as the damped natural frequency of the system. If > 1,
the two roots s1, s2 are real and we have an over damped system. If = 1, the system is known as a critically damped system. The more common case of < 1 is known as the under damped system.
Steady State Errors : One of the important design specifications for a control system is the steady state error. The steady state output of any system should be as close to desired output as possible. If it deviates from this desired output, the performance of the system is not satisfactory
37
under steady state conditions. The steady state error reflects the accuracy of the system. Among many reasons for these errors, the most important ones are the type of input, the type of the system and the nonlinearities present in the system. Since the actual input in a physical system is often a random signal, the steady state errors are obtained for the standard test signals, namely, step, ramp and parabolic signals. Error Constants : Let us consider a feedback control system as shown below.
The error signal E (s) is given by But
E (s) = R (s) - H (s) C (s) C (s) = G (s) E (s)
From the above equations we have
Applying final value theorem, we can get the steady state error ess as,
The above equation shows that the steady state error is a function of the input R(s) and the open loop transfer function G(s). Let us consider various standard test signals and obtain the steady state error for these inputs. Proportional, Integral and Derivative Controller (PID Control) : A ProportionalIntegralDerivative (PID) controller is a three-term controller which is
considered as a standard controller in industrial settings. . It can be found in virtually all kinds of
38
control equipments, either as a stand-alone (single-station)controller or as a functional block in Programmable Logic Controllers (PLCs)and Distributed Control Systems (DCSs). An integral control eliminates steady state error due to a velocity input, but its effect on dynamic response is 'difficult to predict as the system order increases to three. It is known that a derivative term in the forward path improves the damping in the system. One of the best-known controllers used in practice is the PID controller, where the letters stand for proportional, integral,and derivative. The integral and derivative components of the PID controller have individual performance implications, and their applications require an understanding ofthe basics of these elements. Hence a suitable combination of integral and derivative controls results in a proportional, integral and derivate control, usually called PID control. The transfer function of the PID controller is given by,
The diagram below gives the ideal PID controller.
The overall forward path transfer function is given by,
39
and the overall transfer function is given by,
Proper choice of Kp, KD and Kr results in satisfactory transient and steadystate responses. The process of choosing proper Kp, KD, at Kr for a given system is known as tuning of a P ID controller. Bode plots : Bode plots are graphs of the steady state response of stable continuous time Linear time invariant systems for sinusoidal inputs,plotted as change in magnitude and phase versus frequency on logarithmic scale.Bode plots are a visual description of the system.So,these Bode plots are used for the representation of sinusoidal transfer function . In this representation the magnitude of G(j) in db, i.e, 20 log G(j) is plotted against 'log '.Similarly phase angle of G(j) is plotted against 'log ' .Hence the abscissa is logarithm of the frequency and hence the plots are known as logarithmic plots. The plots are named after the famous mathematician H. W. Bode. The transfer function G(j) can be written as G(j) = G(j)( ) Where ( ) is the angle G(j) . Since G(j) consists of many multiplicative factors in the numerator and denominator it is convenient to take logarithm of G(j) to convert these factors into additions and subtractions, which can be carried out easily. To plot the magnitude plot , magnitude is plotted against input frequency on a logarithmic scale.It can be approximated by two lines and it forms the asymptotic (approximate) magnitude Bode plot of the transfer function:
40
(i) for angular frequencies below c it is a horizontal line at 0 dB since at low frequencies the term / c is small and can be neglected, making the decibel gain equation above equal to zero, (ii) for angular frequencies above c it is a line with a slope of 20 dB per decade since at high frequencies the term / c dominates and the decibel gain expression above simplifies to -20 log ( / c ) which is a straight line with a slope of 20 dB per decade. These two lines meet at the corner frequency. From the Bode plot, it can be seen that for frequencies well below the corner frequency, the circuit has an attenuation of 0 dB, corresponding to a unity pass band gain, i.e. the amplitude of the filter output equals the amplitude of the input. Frequencies above the corner frequency are attenuated the higher the frequency, the higher the attenuation. Phase plot The phase Bode plot is obtained by plotting the phase angle of the transfer function given by = - tan
(/c ) Versus , where and c are the input and cutoff angular frequencies
respectively. For input frequencies much lower than corner, the ratio /c is small and therefore the phase angle is close to zero. As the ratio increases the absolute value of the phase increases and becomes 45 degrees when = c As the ratio increases for input frequencies much greater than the corner frequency, the phase angle asymptotically approaches 90 degrees. The frequency scale for the phase plot is logarithmic. The main advantage of using the Bode plots is that multiplication of magnitudes can be converted into addition. Also a simple method of plotting an approximate log-magnitude curve is
41
obtained. It is based on asymptotic approximations. Such approximation by straight line asymptotes is sufficient if only rough information on the frequency response characteristics is is needed.The phase angle curves can be drawn easily if a template for the phase angle curve of 1+j is available. Expanding the low frequency range ,by use of a logarithmic scale for the frequency is very advantageous ,since characteristics at low frequencies are most important in practical systems. The only limitation is ,it is not possible to draw the curve ,right down to zero frequency because of the logarithmic frequency (log 0 = ) .But this do not give any serious problem. Polar plot : This plot is drawn to study the frequency response in polar co-ordinates. The polar plot of a sinusoidal transfer function G(j) is a plot of the magnitude of G(j) Vs the phase of G(j) on polar co-ordinates as is varied from 0 to . Polar graph sheet has concentric circles and radial lines. Concentric circles represent the magnitude. Radial lines represents the phase angles. In polar sheet +ve phase angle is measured in ACW from 00 and -ve phase angle is measured in CW from 00 . To sketch the polar plot of G(j) for the entire range of frequency , i.e., from 0 to infinity, there are four key points that usually need to be known: The start of plot where = 0, The end of plot where = , where the plot crosses the real axis, i.e., Im(G(j)) = 0, and where the plot crosses the imaginary axis, i.e., Re(G(j)) = 0.
Procedure: The following steps are involved in the plotting of Polar graphs Express the given expression of OLTF in (1+sT) form. Get the expressions for | G(j)H(j)| & G(j)H(j). Tabulate various values of magnitude and phase angles for different values of ranging from 0 to . Usually the choice of frequencies will be the corner frequency and around corner frequencies. Choose proper scale for the magnitude circles. Fix all the points in the polar graph sheet and join the points by a smooth curve. Write the frequency corresponding to each of the point of the plot.
42
Gain Margin: Gain Margin is defined as the factor by which the system gain can be increased to drive the system to the verge of instability. For stable systems, gc < pc G(j)H(j) at = pc < 1 GM = in positive dB .
More positive the Gain Margin , more stable is the system
For marginally stable systems,
G(j)H(j) at =pc = 1 GM = 0 dB
gc = pc
For Unstable systems,
gc > pc G(j)H(j) at =pc > 1 GM = in negative dB
Gain is to be reduced to make the system stable The important conclusions are : If the gain is high, the GM is low and the systems step response shows high overshoots and long settling time. On the contrary, very low gains give high GM and PM, but also causes higher ess(Error), higher values of rise time and settling time and in general give sluggish response. Thus we should keep the gain as high as possible to reduce ess and obtain acceptable response speed and yet maintain adequate GM and PM. As a thumb rule an adequate GM of 2 ( ie 6 dB ) and a PM of about 30 is generally considered sufficient enough. If the gain of the system is increased by a factor 1/, then the G(j)H(j) at =pc becomes (1/) = 1 and hence the G(j)H(j) locus pass through -1+j0 point driving the system to the verge of instability
PHASE MARGIN: Phase Margin is defined as the additional phase lag that can be introduced before the system becomes unstable.
43
Let A be the point of intersection of G(j)H(j) plot and a unit circle centered at the origin. Draw a line connecting the points O & A and measure the phase angle between the line OA and +ve real axis. This angle is the phase angle of the system at the gain cross over frequency. G(jgc)H(jgc) = gc If an additional phase lag of PM is introduced at this frequency, then the phase angle G(jgc)H(jgc) will become 180 and the point A coincides with (-1+j0) driving the system to the verge of instability. This additional phase lag is known as the Phase Margin.
For a stable system, the phase margin is positive. A Phase margin close to zero corresponds to highly oscillatory system A polar plot may be constructed from experimental data or from a system transfer function If values of are marked along the contour, a polar plot gives the same information as a Bode plot Usually, the shape of a polar plot is very important as it gives much information about the system.
Relative and absolute stability: A stable system is a dynamic system with a bounded response to a bounded input. A necessary and sufficient condition for a feedback system to be stable is that all the poles of the system transfer function have negative real parts
44
A system is considered marginally stable if only certain bounded inputs will result in a bounded output. In practical systems, it is not sufficient to know that the system is stable but a stable system must meet the specifications of relative stability which is a quantitative measure of how fast the transients die out in the system. Relative stability of a system is usually defined in terms of two design parameters-phase margin and gain margin. The relative stability of a system can be defined as the property that is measured by the relative real part of each root or pair of roots. The relative stability of a system can also be defined in terms of the relative damping coefficients of each complex root pair and, therefore, in terms of the speed of response and overshoot instead of settling time.
Time Domain Analysis Vs Frequency Domain Analysis
Variable frequency, sinusoidal signal generators are readily available and precision measuring instruments are available for measurement of magnitude and phase angle. The time response for a step input is more difficult to measure with accuracy. It is easier to obtain the transfer function of a system by a simple frequency domain test.Obtaining transfer function from the step response is more tedious. If the system has large time constants, it makes more time to reach steady state at each frequency of the sinusoidal input. Hence time domain method is preferred over frequency domain method in such systems. In order to do a frequency response test on a system, the system has to be isolated and the sinusoidal signal has to be applied to the system. This may not be possible in systems which can not be interrupted. In such cases, a step signal or an impulse signal may be given to the system to find its transfer function. Hence for systems which cannot be interrupted, time domain method is more suitable. The design of a controller is easily done in the frequency domain method than in time domain method. For a given set of performance measures in frequency domain , the parameters of the open loop transfer function can be adjusted easily. The effect of noise signals can be assessed easily in frequency domain rather than time domain. The most important advantage of frequency domain analysis is the ability to obtain the relative stability of feedback control systems. The Routh Hurwitz criterion is essentially a time do main method which determines the absolute stability of a system.
45
Since the time response and frequency response of a system are related through Fourier transform , the time response can be easily obtained from the frequency response. The correlation between time and frequency response can be easily established so that the time domain performance measures can be obtained from the frequency domain specifications and vice versa.
Frequency Response of a Control System : To study the frequency response of a control system let us consider second order system with the transfer function,
The steady state sinusoidal response is obtained by substituting s = j in the above equation
Normalising the frequency , with respect to the natural frequency n by defining a variable
We have,
From the above equation the magnitude and angle of the frequency response is obtained as,
and
The time response for a unit sinusoidal input with frequency OJ is given by,
46
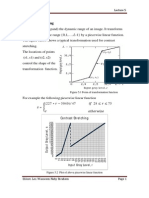
The magnitude and phase of steadystate sinusoidal response for variable frequency can be plotted and are shown in the Fig. (a) and (b).
An important performance measure, in frequency domain, is the bandwidth of the system. From Fig. , we observe that for < 0.707 and U > Ur the magnitude decreases monotonically. The frequency Ub where the magnitude becomes 0.707 is known as the cut off frequency. At this frequency, the magnitude will be
Control system Compensators:

A control system is usually required to meet three time response specifications, namely, steady state accuracy, damping factor and settling time. To get the desired design with minimum errors
47
and to adjust the parameters of the overall system to satisfy the design criterion an additional subsystem called 'Compensator must be used. This compensator may be used in series with the plant in the forward path or in the feedback path shown in Fig. below. The compensation in the forward path is known as series or cascade compensation and the later is known as feedback compensation. The compensator may be a passive network or an active network.
Series compensation
Feedback compensation
In general the series compensation is much simpler than the feed back compensation.But the series compensation frequently require additional amplifiers to increase the gain and to provide isolation.i.e to avoid power dissipation the series compensator is inserted in the lowest energy point in the feed forward path.In general the number of components required in feed back compensation will be less than the number of components in series compensation. There are three important types of compensators.(i) Lead Compensator (ii) Lag compensator and (iii) Lag-Lead compensator. In a network ,when a sinusoidal input signal ei is applied at its input and if the steady state output eo has a phase lead then the network is called a lead network. Similarly In the network for a sinusoidal input ei ,if the steady state output has a phase lag ,then the network is called a lag network. Similarly in a network for a sinusoidal input .if the steady state out put has both phase lag and lead ,but different frequency regions ,then the network is called lag-lead network.Generally the phase lag occurs at low frequency regions and the phase lead occurs at higher frequency region.A compensator having the characteristics of a lead network ,lag network or lead-lag network is called a lead compensator ,lag compensator or lag-lead compensator. The lead compensators, lag compensators and lag-lead compensators are be designed either using electronic components like operational amplifiers or using Root Locus methods. The first
48
type are called electronic lag compensators .The second type are Root locus compensators. The Root locus compensators are have many advantages over electronic type. Lead compensation basically speeds up the response of the control system and increase the stability of the system. Lag compensation improves the steady state accuracy of the system but reduces the speed of the response. If improvements in both transient response and steady state response is required ,both lead compensator and lag compensator are used simultaneously .In general using a single lag-lead compensator is always economical. Lag-lead compensation combines the advantage of lag and lead compensation. Since, the lag lead compensator possesses two poles and two zeros ,such a compensation increases the order of the system by 2 ,unless the cancellation of the poles and zeros occurs in the compensated system.
Lead Compensator : It has a zero and a pole with zero closer to the origin. The general form of the transfer function of the load compensator is
49
Subsisting
Transfer function s
50
Lag Compensator :
It has a zero and a pole with the zero situated on the left of the pole on the negative real axis. The general form of the transfer function of the lag compensator is
Therefore, the frequency response of the above transfer function will be
51
Now comparing with
Therefore,the transfer function is
Lag-Lead Compensator The lag-lead compensator is the combination of a lag compensator and a lead compensator. The lag-section is provided with one real pole and one real zero, the pole being to the right of zero,
52
whereas the lead section has one real pole and one real zero with the zero being to the right of the pole. The transfer function of the lag-lead compensator will be
The figure below shows the lag lead compensator
53
The above transfer functions are comparing with
54
Then
Therefore, the transfer function is given by
state variable analysis :

Analysis and the design of feedback control systems by the classical design methods (root locus and frequency domain methods) based on the transfer function approach are inadequate and not convenient. So, the development of the state-variable approach, took place .This methos has the following advantages over the classical approach.
55
1. It is a direct time-domain approach. Thus, this approach is suitable for digital computer computations 2. It is a very powerful technique for the design and analysis of linear or nonlinear, time-variant or time-invariant, and SISO or MIMO systems. 3. In this technique, the nth order differential equations can be expressed as n equations of first order. Thus, making the solutions easier. 4. Using this approach, the system can be designed for optimal conditions with respect to given performance indices. Definitions: State : The state of a dynamical system is a minimal set of variables x1(t), x2(t)x3(t) xn(t) such that the knowledge of these variables at t = t0 (initial condition), together with the Knowledge of inputs u1(t), u2(t), u3(t) um (t) for t 0, completely determines the behavior of the system for t < t0. State-Variables : The variables x1(t),x2(t),x3(t) xm(t) such that the knowledge of these variables at t = t0 (initial condition), together with the knowledge of inputs u1(t), u2(t), u3(t) um(t) for t t0, completely determines the behavior of the system for t < t0 ; are called state-variables. In other words, the variables that determine the state of a dynamical system, are called state-variables. State-Vector : If n state variables x1(t), x2(t), x3(t) xn(t) are necessary to determine the behavior of a dynamical system, then these n state-variables can be considered as n components of a vector x(t), called state-vector.
State-Space : The n dimensional space, whose elements are the n state-variables, is called statespace. Any state can be represented by a point in the state-space.
State equation of a linear time-invariant system : For a general system of the Figure shown below the state representation can be arranged in the form of n first-order differential equations as
56
(1) Integrating equation 1 , we get
Where I = 1,2,3..n Thus, the n state-variables and, the state of the system can uniquely be determined at any t < tn, provided each state-variable is known at t = tn and all the m control forces are known throughout the interval t 0 to t. The n differential equations of 1 may be written in vector form as (2)
57
Equation 2 is the state equation for time-invariant systems. However, for time-varying systems, the function vector f(.) is dependent on time as well, and the vector equation may be given as .(3) Equation (3) is the state equation for time-varying systems. The output y(t) can, in general, be expressed in terms of the state vector x(t) and input vector u(t) as For time-invariant systems : ----------------------------(4)
For time-varying systems:
----------------(5)
STATE MODEL OF A LINEAR SINGLE-INPUT-SINGLE-OUTPUT SYSTEM: The state model of a linear single-input-single-output system can be written as (1) (2) Where
58
d = Transmission Constant , u(t) = Input or Control Variable (scalar) and, y(t) = Output Variable (scalar). The block-diagram representation of the state model of linear single-input-single-output system is shown below.
A very important conclusion is that the derivatives of all the state-variables are zero at the equilibrium point. Thus, the system continues to lie at the equilibrium point unless otherwise disturbed.
59
SOLUTION OF STATE EQUATIONS FOR LINEAR TIME-INVARIANT SYSTEMS :
The state equation of a linear time-invariant system is given by
For a homogeneous (unforced) system
So , we have Take the Laplace Transform on both sides
..(1)
(2)
The above may also be written as
Taking the inverse Laplace transform
--------------(3)
This equation (3) gives the solution of the LTI homogeneous state Equation.It can be observed that the initial state x(0) at t = 0, is driven to a state x(t) at time t. This transition in state is carried out by the matrix exponential eAt. Because of this property, eAt is termed as the State Transition Matrix and is denoted by (t).
Determination of transfer function using SVA:

Let us consider the following state space equation ,
Now, take the Laplace Transform (with zero initial conditions)
60
We want to solve for the ratio of Y(s) to U(s), which gives the transfer function.So, we need to remove Q(s) from the output equation. We solve the state equation for Q(s)
The matrix (s) is called the state transition matrix. Now , put this into the output equation
Now solving for transfer function ,we get
This is the method of determining the transfer function from state variable analysis (SVA).
--------------------xxxxxxxxxxxxxx------------------------Acknowledgment: Dear Reader, I dont claim any ownership for this material, as it is a collection from various books and websites and other articles. I have simply added my experience and try to provide this material for those people who are preparing for NET/UGC and other Engineering exams.Please download this material for your preparation .But never make it commercial. It is purely meant for students who are in need of this material. References: 1:Automatic control systems - B.C. Kuo, Prentice-Hall of India. 2. Modern Control Engineering- K. Ogata, Prenticd-Hall of India. 3. Control Systems Engineering - I.G. Nagrath, M. Gopal; Wiley Eastern Ltd 4. Control Systems -Second Edition - Dr. N.C. Jagan And many more peoples study material on the net.
61

Control Systems - Notes

Uploaded by

Document Information

Original Title

Copyright

Available Formats

Share this document

Share or Embed Document

Sharing Options

Did you find this document useful?

Is this content inappropriate?

Copyright:

Available Formats

Control Systems - Notes

Uploaded by

Copyright:

Available Formats

Dr.Y.NARASIMHA MURTHY Ph.D yayavaram@yahoo.

Fig.1 .Block diagram of a control system.

Dr.Y.NARASIMHA MURTHY Ph.D yayavaram@yahoo.com

Dr.Y.NARASIMHA MURTHY Ph.D yayavaram@yahoo.com

Dr.Y.NARASIMHA MURTHY Ph.D yayavaram@yahoo.com

Dr.Y.NARASIMHA MURTHY Ph.D yayavaram@yahoo.com

Dr.Y.NARASIMHA MURTHY Ph.D yayavaram@yahoo.com

Dr.Y.NARASIMHA MURTHY Ph.D yayavaram@yahoo.com

Block Diagrammatic Representation :

Dr.Y.NARASIMHA MURTHY Ph.D yayavaram@yahoo.com

Dr.Y.NARASIMHA MURTHY Ph.D yayavaram@yahoo.com

Dr.Y.NARASIMHA MURTHY Ph.D yayavaram@yahoo.com

Dr.Y.NARASIMHA MURTHY Ph.D yayavaram@yahoo.com

Dr.Y.NARASIMHA MURTHY Ph.D yayavaram@yahoo.com

Dr.Y.NARASIMHA MURTHY Ph.D yayavaram@yahoo.com

This is the transfer function of the closed loop control system

Dr.Y.NARASIMHA MURTHY Ph.D yayavaram@yahoo.com

By definition ,the transfer function is G(S) =

Dr.Y.NARASIMHA MURTHY Ph.D yayavaram@yahoo.com

Dr.Y.NARASIMHA MURTHY Ph.D yayavaram@yahoo.com

Dr.Y.NARASIMHA MURTHY Ph.D yayavaram@yahoo.com

Example : A linear system is described by the differential equation

Dr.Y.NARASIMHA MURTHY Ph.D yayavaram@yahoo.com

Dr.Y.NARASIMHA MURTHY Ph.D yayavaram@yahoo.com

Dr.Y.NARASIMHA MURTHY Ph.D yayavaram@yahoo.com

Dr.Y.NARASIMHA MURTHY Ph.D yayavaram@yahoo.com

Dr.Y.NARASIMHA MURTHY Ph.D yayavaram@yahoo.com

Dr.Y.NARASIMHA MURTHY Ph.D yayavaram@yahoo.com

Dr.Y.NARASIMHA MURTHY Ph.D yayavaram@yahoo.com

Dr.Y.NARASIMHA MURTHY Ph.D yayavaram@yahoo.com

Dr.Y.NARASIMHA MURTHY Ph.D yayavaram@yahoo.com

Dr.Y.NARASIMHA MURTHY Ph.D yayavaram@yahoo.com

Dr.Y.NARASIMHA MURTHY Ph.D yayavaram@yahoo.com

Dr.Y.NARASIMHA MURTHY Ph.D yayavaram@yahoo.com

Dr.Y.NARASIMHA MURTHY Ph.D yayavaram@yahoo.com

Dr.Y.NARASIMHA MURTHY Ph.D yayavaram@yahoo.com

Dr.Y.NARASIMHA MURTHY Ph.D yayavaram@yahoo.com

The closed loop transfer function of the system is given by

Dr.Y.NARASIMHA MURTHY Ph.D yayavaram@yahoo.com

For a unit step input R (s) = 1 / s and the output is given by

Inverse Laplace transformation yields

The response is an exponentially increasing function and it approaches a value of unity as

The error E(s) for a unity feedback system is given by

Dr.Y.NARASIMHA MURTHY Ph.D yayavaram@yahoo.com

For the system under consideration G(s) = 1 / s and R(s) = 1 /s

The response of the system for which , R(s) = 1 / s2 is given by

Dr.Y.NARASIMHA MURTHY Ph.D yayavaram@yahoo.com

Differentiating the above equation we get

Dr.Y.NARASIMHA MURTHY Ph.D yayavaram@yahoo.com

Response to a Unit Step Input - Second Order System

The closed loop transfer function is give by,

Dr.Y.NARASIMHA MURTHY Ph.D yayavaram@yahoo.com

is known as the damped natural frequency of the system. If > 1,

Dr.Y.NARASIMHA MURTHY Ph.D yayavaram@yahoo.com

The error signal E (s) is given by But

E (s) = R (s) - H (s) C (s) C (s) = G (s) E (s)

From the above equations we have

Dr.Y.NARASIMHA MURTHY Ph.D yayavaram@yahoo.com

The diagram below gives the ideal PID controller.

The overall forward path transfer function is given by,

Dr.Y.NARASIMHA MURTHY Ph.D yayavaram@yahoo.com

and the overall transfer function is given by,

Dr.Y.NARASIMHA MURTHY Ph.D yayavaram@yahoo.com