MasteringPhysics: Assignment Print View

http://session.masteringphysics.com/myct/assignmentPrint?assignmentI...

Assignment Display Mode:

View Printable Solutions

PHYS2AC, Winter 2006, UC San Diego

Homework-8
Assignment is due at 5:00pm on Tuesday, March 7, 2006
Credit for problems submitted late will decrease to 0% after the deadline has passed. There is no penalty for wrong answers to free response questions. Multiple choice questions are penalized as described in the online help. The unopened hint bonus is 5% per part. You are allowed 7 attempts per answer.

Introduction to Moments of Inertia

Description: Conceptual questions about moment of inertia; several basic computational questions for both discrete and continuous mass distribution. Learning Goal: To understand the definition and the meaning of moment of inertia; to be able to calculate the moments of inertia for a group of particles and for a continuous mass distribution with a high degree of symmetry. By now, you may be familiar with a set of equations describing rotational kinematics. One thing that you may have noticed was the similarity between translational and rotational formulas. Such similarity also exists in dynamics and in the work-energy domain. For a particle of mass moving at a constant speed , the kinetic energy is given by the formula . If we consider instead

a rigid object of mass rotating at a constant angular speed , the kinetic energy of such an object cannot be found by using the formula directly: different parts of the object have different linear speeds. However, they all have the same angular speed. It would be desirable to obtain a formula for kinetic energy of rotational motion that is similar to the one for translational motion; such a formula would include the term instead of . Such a formula can, indeed, be written: for rotational motion of a system of small particles or for a rigid object with continuous mass distribution, the kinetic energy can be written as . Here, is called the moment of inertia of the object (or of the system of particles). It is the quantity representing the inertia with respect to rotational motion. It can be shown that for a discrete system, say of particles, the moment of inertia (also known as rotational inertia) is given by . In this formula, is the mass of the ith particle and is the distance of that particle from the axis of rotation.

For a rigid object, consisting of infinitely many particles, the analogue of such summation is integration over the entire object: . In this problem, you will answer several questions that will help you better understand the moment of inertia, its properties, and its applicability. It is recommended that you read the corresponding sections in your textbook before attempting these questions. Part A On which of the following does the moment of inertia of an object depend? A. linear speed B. linear acceleration C. angular speed

1 of 14

3/8/2006 1:42 AM

MasteringPhysics: Assignment Print View

http://session.masteringphysics.com/myct/assignmentPrint?assignmentI...

D. E. F. G.

angular acceleration total mass shape and density of the object location of the axis of rotation

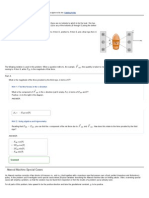
Type the letters corresponding to the correct answers. Do not use commas. For instance, if you think that only assumptions C and D are correct, type CD. ANSWER: EFG Unlike mass, the moment of inertia depends not only on the amount of matter in an object but also on the distribution of mass in space. The moment of inertia is also dependent on the axis of rotation. The same object, rotating with the same angular speed, may have different kinetic energy depending on the axis of rotation. Consider the system of two particles, a and b, shown in the figure . Particle a has mass , and particle b has mass .

Part B What is the moment of inertia of particle a?

ANSWER:

j k l m n
j k l m n

j k l m n i j k l m n

undefined: an axis of rotation has not been specified.

Part C Find the moment of inertia of particle a with respect to the x axis (that is, if the x axis is the axis of rotation), the moment of inertia of particle a with respect to the y axis, and the moment of inertia of particle a with respect to the z axis (the axis that passes through the origin perpendicular to both the x and y axes). Express your answers in terms of ANSWER: Part D Find the total moment of inertia of the system of two particles shown in the diagram with respect to the y axis. Express your answer in terms of ANSWER: = and . , , = and separated by commas.

For parts G to J, suppose that both particles rotate with the same angular speed about the y axis while maintaining their distances from the y axis. Part E Using the total moment of inertia of the system found in Part F, find the total kinetic energy Express your answer in terms of , , and . of the system.

2 of 14

3/8/2006 1:42 AM

MasteringPhysics: Assignment Print View

http://session.masteringphysics.com/myct/assignmentPrint?assignmentI...

ANSWER:

= for the kinetic energy of an

It is useful to see how the formula for rotational kinetic energy agrees with the formula object that is not rotating. To see the connection, let us find the kinetic energy of each particle. Part F Using the formula for kinetic energy of a moving particle energy Part F.1 of particle b. Find the linear speed , find the linear speed of particle a. , find the kinetic energy

of particle a and the kinetic

Using the formula ANSWER:

Express your answer in terms of and . =

Express your answers in terms of , , and separated by a comma. ANSWER: , =

Part G Using the results for the kinetic energy of each particle, find the total kinetic energy Express your answer in terms of , , and . ANSWER: = and give the same result. They should, of course, since the rotational kinetic of the system of particles.

Not surprisingly, the formulas

energy of a system of particles is simply the sum of the kinetic energies of the individual particles making up the system. A system of two (or more) discrete particles is relatively easy to deal with; however, when we analyze an extended object with mass continuously distributed in space, things get trickier. Such an object can be viewed as a system of a very large number of particles, each of a very small mass. To calculate the moment of inertia, one must add a very large number (in the limit, an infinite number) of terms. In the next part, you are asked to perform such a calculation.

The Parallel-Axis Theorem

Description: Contains several simple examples demonstrating that the parallel-axis theorem correctly predicts the values of the moment of inertia. Learning Goal: To understand the parallel-axis theorem and its applications To solve many problems about rotational motion, it is important to know the moment of inertia of each object involved. Calculating the moments of inertia of various objects, even highly symmetrical ones, may be a lengthy and tedious process. ), in most cases it is useful simply While it is important to be able to calculate moments of inertia from the definition ( to recall the moment of inertia of a particular type of object. The moments of inertia of frequently occurring shapes (such as a uniform rod, a uniform or a hollow cylinder, a uniform or a hollow sphere) are well known and readily available from any mechanics text, including your textbook. However, one must take into account that an object has not one but an infinite number of moments of inertia. One of the distinctions between the moment of inertia and mass (the latter being the measure of tranlsational inertia) is that the moment of inertia of a body depends on the axis of rotation. The moments of inertia that you can find in the textbooks are usually calculated with respect to an axis passing through the center of mass of the object. However, in many problems the axis of rotation does not pass through the center of mass. Does that mean that one has to go through the lengthy process of finding the moment of inertia from scratch? It turns out that in many cases, calculating the moment of inertia , where is can be done rather easily if one uses the parallel-axis theorem. Mathematically, it can be expressed as the moment of inertia about an axis passing through the center of mass, is the total mass of the object, and is the moment of

3 of 14

3/8/2006 1:42 AM

MasteringPhysics: Assignment Print View

http://session.masteringphysics.com/myct/assignmentPrint?assignmentI...

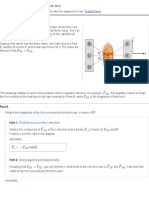
inertia about another axis, parallel to the one for which is calculated and located a distance from the center of mass. In this problem you will show that the theorem does indeed work for at least one object: a dumbbell of length made of two small spheres of mass each connected by a light rod (see the figure). NOTE: Unless otherwise noted, all axes considered are perpendicular to the plane of the page.

Part A Using the definition of moment of inertia, calculate Hint A.1 Hint A.2 Location of the center of mass Finding the moment of inertia for each sphere. . , the moment of inertia about the center of mass, for this object.

The center of mass is halfway between the two spheres, at point A (see the figure). Since each sphere is located at distance from the center of mass, one sphere's individual moment of inertia is Express your answer in terms of ANSWER: Part B Using the definition of moment of inertia, calculate , the moment of inertia about an axis through point B, for this object. Point B coincides with (the center of) one of the spheres (see the figure). Hint B.1 Finding the contribution of each sphere Now the axis of rotation passes through the left sphere, so the moment of inertia due to that sphere is trivially obtained; Also, keep in mind that the right sphere is now located at distance from the axis of rotation. Express your answer in terms of ANSWER: Part C Now calculate for this object using the parallel-axis theorem. , , and . Express your answer in terms of ANSWER: Part D Using the definition of moment of inertia, calculate , the moment of inertia about an axis through point C, for this object. Point C is located a distance from the center of mass (see the figure). Hint D.1 Finding the contribution of each sphere from the axis of rotation. Each sphere is now located a distance Express your answer in terms of ANSWER: = = = and . = and .

and .

4 of 14

3/8/2006 1:42 AM

MasteringPhysics: Assignment Print View

http://session.masteringphysics.com/myct/assignmentPrint?assignmentI...

Part E Now calculate for this object using the parallel-axis theorem. , , and . Express your answer in terms of ANSWER: =

Not surprisingly, the parallel-axis theorem yields the correct result each time! Let us now apply that theorem to a more general case. Consider an irregular object of mass . Its moment of inertia measured with respect to axis A (parallel to the plane of the page), which passes through the center of mass (see the second diagram), is given by . Axes B, C, D, and E are parallel to axis A; their separations from axis A are shown in the diagram. In the subsequent questions, the subscript indicates the axis with respect to which the moment of inertia is measured: for instance, is the moment of inertia about axis C.

Part F Which moment of inertia is the smallest? ANSWER:

i j k l m n
j k l m n

j k l m n j k l m n
j k l m n

One of the important results obtained from the parallel-axis theorem is that for any object, the family of moments of inertia with respect to various parallel axes. Part G Which moment of inertia is the largest? ANSWER:
j k l m n j k l m n
j k l m n

is always the smallest among

j k l m n i j k l m n

Part H Which moments of inertia are equal? ANSWER: and and j k l m n and j No two moments of inertia are equal. k l m n
j k l m n
i j k l m n

Part I

5 of 14

3/8/2006 1:42 AM

MasteringPhysics: Assignment Print View

http://session.masteringphysics.com/myct/assignmentPrint?assignmentI...

Which moment of inertia equals ANSWER:

j k l m n j k l m n
i j k l m n

j k l m n

Part J Axis X, not shown in the diagram, is parallel to the axes shown. It is known that location for axis X? ANSWER: between axes A and C between axes C and D i between axes D and E j k l m n j to the right of axis E k l m n
j k l m n j k l m n

. Which of the following is a possible

Problem 9.46
A light, flexible rope is wrapped several times around a hollow cylinder with a weight of 40.0 N and a radius of 0.25 m, that rotates without friction about a fixed horizontal axis. The cylinder is attached to the axle by spokes of a negligible moment of inertia. The cylinder is initially at rest. The free end of the rope is pulled with a constant force P for a distance of 5.00 m, at which point the end of the rope is moving at 6.00 m/s. Part A If the rope does not slip on the cylinder, what is the value of P? ANSWER: N

Problem 9.68
A classic 1957 Chevrolet Corvette mass 1240 kg starts from rest and speeds up with a constant tangential acceleration of on a circular test track of radius 60.0 m. Treat the car as a particle. Part A What is its angular acceleration? ANSWER: Part B What is its angular speed 6.00 s after it starts? ANSWER: Part C What is its radial acceleration at this time? ANSWER: Part D What is the magnitude of the total acceleration for the car at this time? rad/s

6 of 14

3/8/2006 1:42 AM

MasteringPhysics: Assignment Print View

http://session.masteringphysics.com/myct/assignmentPrint?assignmentI...

ANSWER: Part E What is the magnitude of the net force for the car at this time? ANSWER: Part F What angle do the total acceleration and net force make with the car's velocity at this time? ANSWER: kN

Problem 9.74
A sphere consists of a solid wooden ball of uniform density foil with area density . Part A Calculate the moment of inertia of this sphere about an axis passing through its center. ANSWER: and radius 0.20 m and is covered with a thin coating of lead

Problem 9.76
A thin uniform rod 50.0 cm long and with mass 0.320 kg is bent at its center into a V shape, with a Part A Find the moment of inertia of this V-shaped object about an axis perpendicular to the plane of the V at its vertex. ANSWER: angle at its vertex.

Problem 9.77
It has been argued that power plants should make use of off-peak hours (such as late at night) to generate mechanical energy and store it until it is needed during peak load times, such as the middle of the day. One suggestion has been to store the energy in large flywheels spinning on nearly frictionless ball-bearings. Consider a flywheel made of iron, with a density of , in the shape of a uniform disk with a thickness of . Part A What would the diameter of such a disk need to be if it is to store an amount of kinetic energy of angular velocity of about an axis perpendicular to the disk at its center? ANSWER: when spinning at an

Part B What would be the centripetal acceleration of a point on its rim when spinning at this rate? ANSWER:

7 of 14

3/8/2006 1:42 AM

MasteringPhysics: Assignment Print View

http://session.masteringphysics.com/myct/assignmentPrint?assignmentI...

Problem 9.78
The three uniform objects shown in the figure have the same mass . Object A is a solid cylinder with radius . Object B is a hollow, thin cylinder with radius . Object C is a solid cube whose sides are of length . The axis of rotation of each object is perpendicular to the page and through the object's center of mass.

Part A Which object has the smallest moment of inertia? ANSWER: object A object B j object C k l m n
i j k l m n j k l m n

Part B Which object has the largest moment of inertia? ANSWER: object A object B j object C k l m n
j k l m n i j k l m n

Part C Where would the moment of inertia of a uniform solid sphere rank if its radius is , its mass is , and the axis of rotation is along a diameter of the sphere? ANSWER: the sphere would replace the solid cylinder the sphere would replace the hollow cylinder j the sphere would replace the cube k l m n
i j k l m n j k l m n

Problem 9.88
A passenger bus in Zurich, Switzerland derived its motive power from the energy stored in a large flywheel. The wheel was brought up to speed periodically, when the bus stopped at a station, by an electric motor, which could then be attached to the electric power lines. The flywheel was a solid cylinder with a mass of and a diameter of ; its top angular speed was . Part A At this angular speed, what is the kinetic energy of the flywheel? ANSWER:

Part B If the average power required to operate the bus is , how long could it operate between stops? ANSWER:

8 of 14

3/8/2006 1:42 AM

MasteringPhysics: Assignment Print View

http://session.masteringphysics.com/myct/assignmentPrint?assignmentI...

Problem 9.92
In the figure , the cylinder and pulley turn without friction about stationary horizontal axles that pass through their centers. A light rope is wrapped around the cylinder, passes over the pulley, and has a 3.00-kg box suspended from its free end. There is no slipping between the rope and the pulley surface. The uniform cylinder has mass 5.00 kg and radius 40.0 cm. The pulley is a uniform disk with mass 2.00 kg and radius 20.0 cm. The box is released from rest and descends as the rope unwraps from the cylinder.

Part A Find the speed of the box when it has fallen 1.50 m. ANSWER: m/s

Torque and Angular Acceleration

Description: Calculating the angular acceleration of a rigid object: a seesaw with two masses attached to it. Learning Goal: To understand and apply the formula to rigid objects rotating about a fixed axis. , where is the net force acting on the

To find the acceleration of a particle of mass , we use Newton's second law: particle.

To find the angular acceleration of a rigid object rotating about a fixed axis, we can use a similar formula: is the net torque acting on the object and is its moment of inertia.

, where

In this problem, you will practice applying this formula to several situations involving angular acceleration. In all of these situations, two objects of masses and are attached to a seesaw. The seesaw is made of a bar that has length and is pivoted so that it is free to rotate in the vertical plane without friction. You are to find the angular acceleration of the seesaw when it is set in motion from the horizontal position. In all cases, assume . that Part A The seesaw is pivoted in the middle, and the mass of the swing bar is negligible.

Find the angular acceleration of the seesaw.

Part A.1

Find the moment of inertia , , and .

Find the moment of inertia of the system. Express your answer in terms of some or all of the quantities ANSWER: =

9 of 14

3/8/2006 1:42 AM

MasteringPhysics: Assignment Print View

http://session.masteringphysics.com/myct/assignmentPrint?assignmentI...

Part A.2

Find the net torque , , , as well as the acceleration due to gravity .

Find the magnitude of the net torque acting on the system. Express your answer in terms of some or all of the quantities ANSWER: = , , , as well as the acceleration due to gravity .

Express your answer in terms of some or all of the quantities ANSWER: =

Part B In what direction will the seesaw rotate, and what will the sign of the angular acceleration be? ANSWER: The rotation is in the clockwise direction and the angular acceleration is positive. The rotation is in the clockwise direction and the angular acceleration is negative. i The rotation is in the counterclockwise direction and the angular acceleration is positive. j k l m n j The rotation is in the counterclockwise direction and the angular acceleration is negative. k l m n
j k l m n
j k l m n

Part C Now consider a similar situation, except that now the swing bar itself has mass .

Find the angular acceleration of the seesaw.

Part C.1

What has changed?

Compared to the previous situation, what quantities have changed? ANSWER: net torque only moment of inertia only j both torque and moment of inertia k l m n
j k l m n i j k l m n

In calculating the torque due to gravity, the weight of the bar is applied at the center of mass of the bar. The distance between the center of mass and the pivot is used in the calculation of the torque. In this case, the center of mass of the bar coincides with the pivot point. Therefore, the corresponding torque is zero. Part C.2 Find the moment of inertia and length , pivoted

What is the new moment of inertia ? Recall that the moment of inertia for a uniform thin rod of mass at its center, is given by . Express your answer in terms of some or all of the quantities ANSWER: = , , , , , and .

Express your answer in terms of some or all of the quantities ANSWER: =

, , as well as the acceleration due to gravity .

10 of 14

3/8/2006 1:42 AM

MasteringPhysics: Assignment Print View

http://session.masteringphysics.com/myct/assignmentPrint?assignmentI...

Part D In what direction will the seesaw rotate and what will the sign of the angular acceleration be? ANSWER: The rotation is in the clockwise direction and the angular acceleration is positive. The rotation is in the clockwise direction and the angular acceleration is negative. i The rotation is in the counterclockwise direction and the angular acceleration is positive. j k l m n j The rotation is in the counterclockwise direction and the angular acceleration is negative. k l m n
j k l m n j k l m n

Part E This time, the swing bar of mass

is pivoted at a different point, as shown in the figure.

Find the magnitude of the angular acceleration of the swing bar. Be sure to use the absolute value function in your answer, since no comparison of , , and has been made.

Part E.1

What has changed?

Compared to the previous situation, what quantities have changed? ANSWER: net torque only moment of inertia only i both torque and moment of inertia j k l m n
j k l m n j k l m n

This time, the torque due to the weight of the bar is not zero. Additionally, the torques due to the weights of the blocks are different, since their lever arms have changed. Part E.2 Find the moment of inertia Find the total moment of inertia of the bar and the two masses. Part E.2.a Find the moment of inertia of the bar alone What is the moment of inertia of the bar alone? Hint E.2.a.i Use the parallel-axis theorem The moment of inertia of a uniform bar of mass and length about the axis passing through the midpoint (center of mass) of the bar and perpendicular to the it (as in the previous situation) is . In the current situation, the axis passes at distance from the center of mass. The value of the moment of inertia with respect to this new axis can be determined using the parallel-axis theorem: , where is the moment of inertia of a body of mass about an axis through its center of mass, and is the moment of inertia of that object through an axis parallel to the original axis through its center of mass, but displaced from it by a distance . Express your answer in terms of ANSWER: = , , , and . and .

Express your answer in terms of some or all of the quantities

11 of 14

3/8/2006 1:42 AM

MasteringPhysics: Assignment Print View

http://session.masteringphysics.com/myct/assignmentPrint?assignmentI...

ANSWER:

= Find the net torque

Part E.3

Find the magnitude of the net torque acting on the system. Be sure to use the absolute value function in your answer, since no comparison of , , and has been given. Express your answer in terms of some or all of the quantities , , , , as well as the acceleration due to gravity . Enter the absolute value function abs(). For instance, enter abs(x*y) for . ANSWER: = , , and , we cannot determine the direction of the net torque.

Since we cannot numerically compare the quantities

Express your answer in terms of some or all of the quantities , , , , as well as the acceleration due to gravity . Enter the absolute value function as abs(). For instance, enter abs(x*y) for . ANSWER: = , , and , we cannot determine the direction of rotation or the

Since we cannot numerically compare the quantities sign of the angular acceleration. Part F If is 24 kilograms, acceleration? ANSWER:
j k l m n i j k l m n

is 12 kilograms, and

is 10 kilograms, what is the direction of rotation and the sign of the angular

The rotation is in the clockwise direction and the angular acceleration is positive. The rotation is in the clockwise direction and the angular acceleration is negative. j The rotation is in the counterclockwise direction and the angular acceleration is positive. k l m n j The rotation is in the counterclockwise direction and the angular acceleration is negative. k l m n

Problem 10.4
Forces and are applied tangentially to a wheel with radius 0.330 m, as shown in the figure .

Part A What is the net torque on the wheel due to these two forces for an axis perpendicular to the wheel and passing through its center? ANSWER:

Problem 10.19

12 of 14

3/8/2006 1:42 AM

MasteringPhysics: Assignment Print View

http://session.masteringphysics.com/myct/assignmentPrint?assignmentI...

A string is wrapped several times around the rim of a small hoop with radius and mass . The free end of the string is held in place and the hoop is released from rest .

Part A Calculate the tension in the string while the hoop descends as the string unwinds. Take free fall acceleration to be . ANSWER:

Part B Calculate the time it takes the hoop to descend a distance . ANSWER:

Part C Calculate the angular speed of the rotating hoop after it has descended a distance . ANSWER:

Problem 10.26
A Ball Rolling Uphill. A bowling ball rolls without slipping up a ramp that slopes upward at an angle to the horizontal. Treat the ball as a uniform, solid sphere, ignoring the finger holes. Part A What is the acceleration of the center of mass of the ball? ANSWER:

Part B What minimum coefficient of static friction is needed to prevent slipping? ANSWER:

Problem 10.61
The mechanism shown in the figure is used to raise a crate of supplies from a ship's hold. The crate has total mass 46.0 . A rope is wrapped around a wooden cylinder that turns on a metal axle. The cylinder has about the axle. The crate is suspended radius 0.300 and a moment of inertia = 3.10 from the free end of the rope. One end of the axle pivots on frictionless bearings; a crank handle is attached to the other end. When the crank is turned, the end of the handle rotates

13 of 14

3/8/2006 1:42 AM

MasteringPhysics: Assignment Print View

http://session.masteringphysics.com/myct/assignmentPrint?assignmentI...

about the axle in a vertical circle of radius 0.120 , the cylinder turns, and the crate is raised.

Part A What magnitude of the force 0.750 applied tangentially to the rotating crank is required to raise the crate with an acceleration of ? (You can ignore the mass of the rope as well as the moments of inertia of the axle and the crank.)

ANSWER:

Summary

0 of 15 problems complete (0% avg. score) 0 of 150 points

14 of 14

3/8/2006 1:42 AM