Professional Documents
Culture Documents
Guide For MATLAB
Uploaded by
MOHAMMAD HASHIM KHANOriginal Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Guide For MATLAB
Uploaded by
MOHAMMAD HASHIM KHANCopyright:
Available Formats
Creating GUIs in Matlab
GUIDE GUIDE or the Graphical User Interface development environment is a tool for laying out and programming GUIs. A GUI uses graphics and text input to make using Matlab much more user friendly for people who are unfamiliar with it. GUIs can be created without using GUIDE but laying out the design of the window can be very time consuming. To open GUIDE click on the start button in the bottom left corner of Matlab and select STARTMATLABGUIDE or by clicking
Example GUI This example GUI will allow the user to enter the coecients and boundary values of a dierential equation and well as an error estimate. To start open GUIDE and select the blank GUI option. An empty GUI template opens which you can resize and add controls to, (Figure 1). the number of mesh points N, and then display a plot of the nite dierence approximation to the equation as
Figure 1:
Layout of the controls To display the names of the GUI components in the component palette, select FilePreferences and select Show names in component palette.
Figures Click on the axes button to insert a gure (Figure 2). Clicking on the blank gure window and then on the property inspector button, opens a window displaying options which can be changed. For example scroll
down to Tag and change this to the name which you will reference your plot with (Figure 3)
Figure 2:
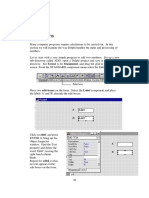
Text Boxes There are two types of text boxes, a static text box and an edit text box. To group all the controls together we can insert a panel around them using the panel button. Select the static text and insert a static text box into the GUI. The property inspector can be used to change the text that is displayed by editing the String option. Change this to u (x)+ r(x)u(x)= f(x). It is useful to change the Tag as well. Also insert a static text box which will display the error estimate (with a tag such as error text). See Figure 4.
""
We have used an edit box to enter the functions r(x), f(x) and the boundary values u(0) and u(1). For example, rst insert a static text box with the string r(x) = and beside it an edit text box with a blank string. Also change the tag to a meaningful name such as r edit. Repeat the process for f(x), u(0) and u(1). See Figure 5.
Figure 3:
Figure 4:
Pop Up Menu The user can select an a variable from a range of options using a pop up menu. To select N we have inserted a static text box with the string N = beside a pop up menu, Figure 5. Change the string of the pop up menu by clicking on the button next to string and entering 4,8,16 etc, hitting return after each new option. Also change the tag to a name such as N pop up.
Push Button Finally insert a push button which will execute some code when clicked. The layout should now look something like Figure 7.
Creating the GUI gure Once all of the controls are inserted as dierential equation. Programming the GUI Clicking on the edit M-le button, particular function. , in GUIDE will open the automatically generated le which controls the , to skip to a click on in GUIDE to create the .g and .m les. Our GUI is saved aaa
actions of the GUI. You can scroll down the le to edit the functions or use the function button,
OpeningFcn The opening function is the rst callback in every GUI M-le. You can use it to perform tasks that need to be done before the user has access to the GUI, for example, to create data or to read data from an external source. In our example the opening function is called dierential equation OpeningFcn. saved in the handles structure. % ---Executes just before differential_equation is made visible. function differential_equation_OpeningFcn(hObject, eventdata, handles, varargin) % This function has no output args, see OutputFcn. % hObject handle to figure % eventdata reserved -to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA) % varargin command line arguments to differential_equation (see VARARGIN) handles.N = 4; handles.x = 0:1/handles.N:1;
At the start we want to set N = 4. Any data that you want to pass between functions in the GUI should be
% Choose default command line output for differential_equation handles.output = hObject; % Update handles structure guidata(hObject, handles); Note that to save any changes that you make to the handles structure, you must insert at the end of each function guidata(hObject,handles);
Figure 5:
Figure 6:
Read in data from an edit text box In order to read information from an edit box we use the command get(hObject,String) inside the callback function. For example to read in the value of u(0) (where the Tag used was u0 edit): function u0_edit_Callback(hObject, eventdata, handles)
% Hints: get(hObject,String) returns contents of u0_edit as text % str2double(get(hObject,String)) returns contents of u0_edit as a double handles.u0 = str2double(get(hObject,String)); % Update handles structure guidata(hObject, handles); To read in the values for the functions r(x) and f(x) we must convert the string to an inline function using handles.f = inline( get(hObject,String), x);
Read in data from a Pop Up menu In order to read in the value of N which is selected in the pop up menu and then create a mesh add this code to the callback % ---Executes on selection change in popupmenu1. function N_popup_Callback(hObject, eventdata, handles) % hObject handle to popupmenu1 (see GCBO) % eventdata reserved -to be defined in a future version of MATLAB % handles structure with handles and user data (see GUIDATA) % Hints: contents = get(hObject,String) returns popupmenu1 contents as cell array % contents{get(hObject,Value)} returns selected item from popupmenu1 val = get(hObject,Value); str = get(hObject, String); handles.N = str2double(str{val}); handles.x = 0:1/handles.N:1; guidata(hObject,handles)
Submit button In order to calculate the nite dierence approximation using your own function and then plot the outcome
include the following into your submit button callback.
% ---Executes on button press in submit_button. function submit_button_Callback(hObject, eventdata, handles)
% use the finite difference method handles.u = fd(handles.r, handles.f, handles.u0, handles.u1,handles.x); plot(handles.x, handles.u);
% estimate the error by comparing to the finite difference % solution using double the mesh points x2 = 0:1/(2*handles.N):1; u2 = fd(handles.r, handles.f, handles.u0, handles.u1, x2); u_interp = interp1( handles.x,handles.u, x2 ); error = max(abs( u_interp -u2));
% display the error set(handles.error_text, String, strcat(error = ,num2str(error)));
% Update handles structure guidata(hObject, handles);
When all the necessary callback functions have been edited save the M-le and run the GUI using the green button. You can also run the GUI by typing differential equation in the command line of Matlab.
Figure 7:
You might also like
- Creating GUI's in Matlab: 1 GuideDocument8 pagesCreating GUI's in Matlab: 1 Guidemfarouk1No ratings yet
- Lab # 9 Introduction To MATLAB Graphical User Interface (GUI)Document8 pagesLab # 9 Introduction To MATLAB Graphical User Interface (GUI)yash523No ratings yet
- Lab # 9 Introduction To MATLAB Graphical User Interface (GUI)Document8 pagesLab # 9 Introduction To MATLAB Graphical User Interface (GUI)abraham_dqhausNo ratings yet
- MATLAB GUI (Graphical User Interface) Tutorial For BeginnersDocument61 pagesMATLAB GUI (Graphical User Interface) Tutorial For BeginnersAnup ShuklaNo ratings yet
- A4-Gui Tutorial PDFDocument36 pagesA4-Gui Tutorial PDFRahmi FebrianiNo ratings yet
- GUI LayoutDocument22 pagesGUI LayoutRodrigo Espinoza CorsNo ratings yet
- MATLAB GUI (Graphical User Interface) Tutorial For BeginnersDocument14 pagesMATLAB GUI (Graphical User Interface) Tutorial For BeginnerssuryaNo ratings yet
- ECE 371 GUI Design in MATLABDocument20 pagesECE 371 GUI Design in MATLABJohnbosco ChideraNo ratings yet
- Exercises GUIDocument20 pagesExercises GUIsharmiNo ratings yet
- Matlab Gui Tutorial by Dr. S.S.Limaye: Why Use GUI (Graphical User Interface) ?Document10 pagesMatlab Gui Tutorial by Dr. S.S.Limaye: Why Use GUI (Graphical User Interface) ?Venicia HawachNo ratings yet
- Brief Guide To Creating A Matlab GUI ApplicationDocument3 pagesBrief Guide To Creating A Matlab GUI ApplicationMeToolNo ratings yet
- Lecture 06Document12 pagesLecture 06Farwa SheikhNo ratings yet
- Program MATLAB GUI ReferenceDocument3 pagesProgram MATLAB GUI ReferenceAhmad_Othman3No ratings yet
- MATLAB and LABView - Chapter 6Document42 pagesMATLAB and LABView - Chapter 6vinh quocNo ratings yet
- Matlab GUI TutorialDocument9 pagesMatlab GUI TutorialBaher MawlawiNo ratings yet
- GUI Building For Test & Measurement Applications: Phase 1: Displaying Acquired Data To An AxisDocument23 pagesGUI Building For Test & Measurement Applications: Phase 1: Displaying Acquired Data To An Axisnguyen1192No ratings yet
- Chapter 1Document22 pagesChapter 1tiger_lxfNo ratings yet
- Mod 7 GUIDocument21 pagesMod 7 GUIJay TolentinoNo ratings yet
- DC Lab 06Document14 pagesDC Lab 06photoid user1No ratings yet
- GUI & SIMULINK ExperimentDocument19 pagesGUI & SIMULINK ExperimentTrương Văn TrọngNo ratings yet
- Introduction to MATLAB for Signal PlottingDocument8 pagesIntroduction to MATLAB for Signal PlottingRadu NiculaeNo ratings yet
- GeoGebraScript Tutorial: Introduction to Commands, Scripting, Buttons, Input BoxesDocument7 pagesGeoGebraScript Tutorial: Introduction to Commands, Scripting, Buttons, Input BoxesNACHIKETH89No ratings yet
- Variable. A Variable May Also Point To An Array of Numbers or Strings. in Lab 5Document3 pagesVariable. A Variable May Also Point To An Array of Numbers or Strings. in Lab 5azqqNo ratings yet
- Image Rotation Using Graphical User InterfaceDocument5 pagesImage Rotation Using Graphical User InterfaceUmeshNo ratings yet
- GUIDocument35 pagesGUIAndac KizilirmakNo ratings yet
- DIP Lab 3Document10 pagesDIP Lab 3Golam DaiyanNo ratings yet
- Learningmathcadchapter1 PDFDocument22 pagesLearningmathcadchapter1 PDFBalaji NatarajanNo ratings yet
- AWT Components: Button (Java - Awt.button)Document22 pagesAWT Components: Button (Java - Awt.button)NoelEkkaNo ratings yet
- Workbook3 Tutorial GeogebraDocument11 pagesWorkbook3 Tutorial GeogebraHarunAbdulRohmanNo ratings yet
- Tugas 5 Piranti Lunak Telekomunikasi LanjutDocument10 pagesTugas 5 Piranti Lunak Telekomunikasi LanjutIndra WigunaNo ratings yet
- TUGAS 2 Citra - HanzhalahDocument9 pagesTUGAS 2 Citra - HanzhalahHanzhalah RamadhanNo ratings yet
- Building Gui & Solving Odes: Introduction To Matlab & Data AnalysisDocument43 pagesBuilding Gui & Solving Odes: Introduction To Matlab & Data AnalysischinmayagubbiNo ratings yet
- Matlab Gui Tutorial - For BDocument89 pagesMatlab Gui Tutorial - For BNishantMehta40No ratings yet
- Session 12b3 Use of The MATLAB Graphical User Interface Development Environment For Some Control System ApplicationsDocument5 pagesSession 12b3 Use of The MATLAB Graphical User Interface Development Environment For Some Control System ApplicationsVivek GoyalNo ratings yet
- Matlab Guide to Solving Equations and Plotting DataDocument26 pagesMatlab Guide to Solving Equations and Plotting DataBlueNo ratings yet
- Chapter 6 P1Document62 pagesChapter 6 P1john1x96No ratings yet
- GUI Layout Managers and ComponentsDocument48 pagesGUI Layout Managers and ComponentsBalasaheb ChavanNo ratings yet
- How To Plot A Projectile Motion Using Mat Lab (Penn State Students)Document8 pagesHow To Plot A Projectile Motion Using Mat Lab (Penn State Students)api-289381545No ratings yet
- Infromática CalcDocument7 pagesInfromática CalcCristina ChivaNo ratings yet
- تطبيقات - الحاسوب - Computer application 9Document24 pagesتطبيقات - الحاسوب - Computer application 9yousifNo ratings yet
- Bab I PermasalahanDocument11 pagesBab I PermasalahanDevia Meliana IndrasariNo ratings yet
- MatLab and Solving EquationsDocument170 pagesMatLab and Solving EquationsJulia-e Regina-e AlexandreNo ratings yet
- FourDocument14 pagesFourAnis GhabriNo ratings yet
- Formatting Functions: Visual BasicDocument17 pagesFormatting Functions: Visual BasicCrysvenneBisligNo ratings yet
- Matlab 5Document38 pagesMatlab 5Shruti YashNo ratings yet
- PS 7Document11 pagesPS 7Arman ChhagNo ratings yet
- PYTHONNANGCAO LAB GUI LamThemDocument42 pagesPYTHONNANGCAO LAB GUI LamThemĐặng Thanh CườngNo ratings yet
- Heap Sort Applet AnimationDocument18 pagesHeap Sort Applet AnimationSimana PerieNo ratings yet
- Class 4 GUIDocument17 pagesClass 4 GUIelad kotlovskiNo ratings yet
- Adding Menus and Sub Menus in An Application: Menu Controls Replace and Add Functionality To The Menu-Related Controls ofDocument20 pagesAdding Menus and Sub Menus in An Application: Menu Controls Replace and Add Functionality To The Menu-Related Controls ofCatherine Flores JimenezNo ratings yet
- GUI Programming: Readings: Savitch, Chapter 12Document36 pagesGUI Programming: Readings: Savitch, Chapter 12mhòa_43No ratings yet
- Function VarargoutDocument18 pagesFunction VarargoutNataliaNo ratings yet
- Using MATLAB For Calculations in BraidingDocument19 pagesUsing MATLAB For Calculations in BraidingHgnNo ratings yet
- Python Advanced Programming: The Guide to Learn Python Programming. Reference with Exercises and Samples About Dynamical Programming, Multithreading, Multiprocessing, Debugging, Testing and MoreFrom EverandPython Advanced Programming: The Guide to Learn Python Programming. Reference with Exercises and Samples About Dynamical Programming, Multithreading, Multiprocessing, Debugging, Testing and MoreNo ratings yet
- Separation Technology For The Chemical Process IndustryDocument24 pagesSeparation Technology For The Chemical Process IndustryDushyant BhosaleNo ratings yet
- Boiler - Problems and SolutionDocument44 pagesBoiler - Problems and SolutionNguyen HoaNo ratings yet
- Numerical Simulation of Methane Partial Oxidation in The Burner and Combustion Chamber of Autothermal ReformerDocument11 pagesNumerical Simulation of Methane Partial Oxidation in The Burner and Combustion Chamber of Autothermal ReformerMOHAMMAD HASHIM KHAN100% (1)
- Role and Influence of Partitioning and Transmutation On The Management of Nuclear WasteDocument7 pagesRole and Influence of Partitioning and Transmutation On The Management of Nuclear WasteMOHAMMAD HASHIM KHANNo ratings yet
- Cu Carry Over To BoilerDocument8 pagesCu Carry Over To BoilerlalindaNo ratings yet
- P&ID Process Diagram GuideDocument5 pagesP&ID Process Diagram GuideMOHAMMAD HASHIM KHANNo ratings yet
- Training ReportIndustrial Training Report On Mejia Thermal Power StationDocument40 pagesTraining ReportIndustrial Training Report On Mejia Thermal Power StationMOHAMMAD HASHIM KHANNo ratings yet
- Packed N Fluidized BedDocument6 pagesPacked N Fluidized BedhariprakavNo ratings yet
- P&ID Process Diagram GuideDocument5 pagesP&ID Process Diagram GuideMOHAMMAD HASHIM KHANNo ratings yet
- Right To Information - Hindi (INDIA) PDFDocument27 pagesRight To Information - Hindi (INDIA) PDFMOHAMMAD HASHIM KHANNo ratings yet
- Catalytic Membrane ReactorDocument29 pagesCatalytic Membrane ReactorMOHAMMAD HASHIM KHAN100% (1)
- Creating GUI's in Matlab: GuideDocument7 pagesCreating GUI's in Matlab: GuideMOHAMMAD HASHIM KHANNo ratings yet
- Simulation of The Catalytic Partial Oxidation of Methane To Synthesis Gas by D.groote, FromentDocument20 pagesSimulation of The Catalytic Partial Oxidation of Methane To Synthesis Gas by D.groote, FromentMOHAMMAD HASHIM KHAN100% (1)
- Herschel-Bulkley Fluid Model ExplainedDocument5 pagesHerschel-Bulkley Fluid Model ExplainedMOHAMMAD HASHIM KHANNo ratings yet
- Rail Budget 2012-13Document7 pagesRail Budget 2012-13NDTVNo ratings yet
- Autothermal Reforming of Simulated Gasoline and Diesel FuelsDocument8 pagesAutothermal Reforming of Simulated Gasoline and Diesel FuelsMOHAMMAD HASHIM KHANNo ratings yet
- Samall Oil Burner in Concepts in Low P (Ressure AutomationDocument10 pagesSamall Oil Burner in Concepts in Low P (Ressure AutomationMOHAMMAD HASHIM KHANNo ratings yet