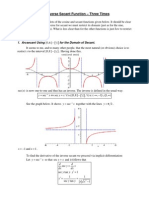
Shearing Force

The shearing force (SF) at any section of a beam represents the tendency for the portion of the beam on one side of the section to slide or shear laterally relative to the other portion.

The diagram shows a beam carrying loads points where the reactions are

. It is simply supported at two Assume that the beam is divided into two parts

by a section XX The resultant of the loads and reaction acting on the left of AA is F vertically upwards and since the whole beam is in equilibrium, the resultant force to the right of AA must be F downwards. F is called the Shearing Force at the section AA. It may be defined as follows:The shearing force at any section of a beam is the algebraic sum of the lateral components of the forces acting on either side of the section. Where forces are neither in the lateral or axial direction they must be resolved in the usual way and only the lateral components use to calculate the shear force.

Bending Moments

In a similar manner it can that if the Bending moments (BM) of the forces to the left of AA are clockwise then the bending moment of the forces to the right of AA must be anticlockwise. Bending Moment at AA is defined as the algebraic sum of the moments about the section of all forces acting on either side of the section Bending moments are considered positive when the moment on the left portion is clockwise and on the right anticlockwise. This is referred to as a sagging bending moment as it tends to make the beam concave upwards at AA. A negative bending moment is termed hogging.

Types Of Load

A beam is normally horizontal and the loads vertical. Other cases which occur are considered to be exceptions. A Concentrated load is one which can be considered to act at a point although of course in practice it must be distributed over a small area. A Distributed load is one which is spread in some manner over the length or a significant length of the beam. It is usually quoted at a weight per unit length of beam. It may either be uniform or vary from point to point.

Types Of Support
A Simple or free support is one on which the beam is rested and which exerts a reaction on the beam. It is normal to assume that the reaction acts at a point although it may in fact act act over a short length of beam.

A Built-in or encastre' support is frequently met . The effect is to fix the direction of the beam at the support. In order to do this the support must exert a "fixing" moment M and a reaction R on the beam. A beam which is fixed at one end in this way is called a Cantilever. If both ends are fixed in this way the reactions are not statically determinate. In practice it is not usually possible to obtain perfect fixing and the fixing moment applied will be related to the angular movement of the support. When in doubt about the rigidity it is safer to assume that the beam is freely supported.

The Relationship Between W; F; M.

In the following diagram the origin O is the length of a small slice of a loaded beam at a distance x from

Let the shearing force at the section x is F and at bending moment is M at x and the length , the total load is

. Similarly the . If w if the mean rate of loading of

, acting approximately ( exactly if uniformly distributed)

through the centre C. The element must be in equilibrium under the action of these forces and couples and the following equations can be obtained:Taking Moments about C (1) Neglecting the product in the limit:(2) Resolving vertically:(3) (4) (5) From equation (2) it can be seen that if M is varying continuously zero shearing force corresponds to either maximum or minimum bending moment. It ca be seen from the examples that "peaks" in the bending moment diagram frequently occur at concentrated loads

or reactions and these are not given by

although they may in fact represent

the greatest bending moment on the beam. Consequently it is not always sufficient to investigate the points of zero shearing force when determining the maximum bending moment. At a point on the beam where the type of bending is changing from sagging to hogging, the bending moment must be zero and this is called a point of inflection or contraflexure. By integrating equation (2) between the x = a and x = b then:-

(6)

Which shows that the increase in bending moment between two sections is the area under the shearing force diagram. Similarly integrating equation (4)

(7) equals the area under the load distribution diagram. Integrating equation (5) gives:-

(8) These relations can be very valuable when the rate of loading cannot be expressed in an algebraic form as they provide a means of graphical solution.

Concentrated Loads
Example 1: A Cantilever of length l carries a concentrated load W at its free end. Draw the Shear Force (SF)and Bending Moment (BM)diagrams. Consider the forces to the left of a section at a distance x from the free end. Then F = - W and is constant along the whole cntilever i.e. for all values of x Taking Moments about the section gives M = - W x so that the maximum Bending Moment occurs when x = l i.e. at the fixed end. (9) From equilibrium considerations it can be seen that the fixing moment applied at the built in end is WL and the reaction is W. Hence the SF and BM diagrams are as follows:-

Example 2: A beam 10 ft. long is simply supported at its ends and carries concentrated loads of 3 tons and 5 tons at distances of 3 ft. from each end. Draw the S.F. and B.M. diagrams.

It is first necessary to calculated the values of the reactions at the supports. Take Moments about B (10) (11) (12) If x is the length of a section measured from the left hand end then:Shearing force (13) (14) (15) It should be noticed that the last value workings. Bending Moments (16) (17) (18) which provides a check on the

The principle values of M at x = 3 ft.are M = 10.8 tons-ft.and at x = 7 M = 10.8 tons-ft. Note that the latter value can be checked by taking are involved. as calculated for the right-hand portion. The following general conclusions can be drawn when only concentrated loads and reactions

The shearing force suffers sudden canges when passing through a load point,. The change is equal to the load.

The bending Moment diagram is a series of straight lines between loads. The slope of the lines is equal to the shearing force between the loading points

Uniformly Distributed Loads

Example 3: Draw the SF and BM diagrams for a Simply supported beam of length l carrying a uniformly distributed load w per unit length which occurs across the whole Beam. The Total Load carried is wl and by symmetry the reactions at both end supports are each wl/2 If x is the distance of the section measured from the left-hand support then:-

(19) This give a straight line graph equal to the rate of loading. The end values of Shearing Force

are The Bending Moment at the section is found by assuming that the distributed load acts through its centre of gravity which is x/2 from the section.

(20)

(21)

This is a parabolic curve having a value of zero at each end. The maximum is at the centre and corresponds to zero shear force From Equation (2)

(22) Putting x = l/2 (23)

Combined Loads.
Example 4:

A Beam 25 ft. long is supported at A and B and is loaded as shown. Sketch the SF and BM diagrams and find (a) the position and magnitude of the maximum Bending Moment and (b) the position of the point of contraflexure. Taking Moments about B (24) (The distributed load is taken as acting at its centre of gravity.) (25) (2 6) The Shearing Force Starting at A F = 7.25. As the section moves away from A F decreases at a uniform rate of w per unit length ( i.e. f = 7.25 - wx) and reaches a value of - 2.75 at E. Between E and D, F is constant ( There is no load on Ed) and at D it suffers a sudden decrease of 2 tons ( the load at D) . Similarly there is an increase at B of 7.75 tons ( the reaction at B). This results in a value of F = 3 tons at B which remains constant between B and C. Note this value agrees with the load at C.

Bending Moment From A to E:(27) This is a parabola which can be sketched by taking several values of x. Beyond E the value of x for the distributed load remains constant at 5 ft. from A

Between E and D (28) This produces a straight line between E and D. Similar equations apply for sections DB and BC. However it is only necessary to evaluate M at the points D and B since M is zero at C. The diagram consists in straight lines between these values. (29) (30) This last value was calculated for the portion BC We were required to find the position and magnitude of the maximum BM. This occurs where the shearing force is zero. i.e.at 7.25 ft. from A (31) The point of contraflexure occurs when the bending moment is zero and this is between D and B at:-

(32)

Example 5: A girder 30 ft. long carrying a uniformly distributed load of w ton/ft. is to be supported on two piers 18 ft. apart so that the greatest Bending Moment will be as small as possible. Find the distance of the piers from the ends of the girder and the Maximum B.M. (U.L.) Let the distance of one pier be d ft.from the end of the girder. Hence the other overhang will be 12 - d.

Taking Moments about the right-hand support. The distance of the centre of the girder from the right-hand support is (3 + d):-

(33)

(34) For the overhanging end which gives a maximum value at the support of :(35) For the portion between the supports:(36) This is a maximum when (37) Using this equation and equation (34):-

(38)

(39)

(40)

(41) For the greatest BM to be as small as possible is is necessary to make the two values numerically equal. It is clear that if the supports are moved to the right of this position the value at the left support will increase and if it is moved to the left the value between the supports will increase. Equating the numerical values from equations (34) and (41) (42)

(43)

(44) Solving:-

(45) And for the other support:(46) From equation (34) (47) (48) Example 6: Draw the SF and BM diagrams for a beam 8 ft. long simply supported at its ends, carrying a load of 2 tons which is applied through a bracket. The bracket is fixed to the beam at a distance 0f 6ft. from one support, the length of bracket in the direction of the beam being 1 ft.

Taking Moments about the right hand end:(49) The effect of the bracket is to apply a load of 2 tons and a B.M. of 2 ton_t at a point 6 ft. from the left hand end. Thus F has a value of 3/4 tons along 6 ft. of the beam from the left-hand end and fro the other two foot M increases from zero to at the bracket on the other side. There is

a sudden change in Bending Moment at the bracket equal to 2 tons-ft.

Varying Distributed Loads.

Example 7: A Beam ABC, 27 ft. long, is simply supported at A and B 18 ft. across and carries a load of 2 tons at 6 ft. from A together with a distributed load whose intensity varies in linear fashion from zero at A and C to 1ton/ft. at B. Draw the Shear Force and Bending Moment diagrams and calculate the position and magnitude of the maximum B.M. (U.L.) The Total Load on the beam ( i.e. the load plus the mean rate of loading of 1/2 tons/ft) is given by:(50)

The Total distribute load on

and on

each of which act through their centres of gravity. These are

from A and

from C in the other case. (Note. These are

the centroids of the triangles which represent the load distribution)

Taking Moments about B

(51) (52) At a distance x (<18)from A the loading is x/18 tons/ft.. The Total distributed load on this length is:(53) The centre of gravity of this load is For 0<X<6< strong> (54) At x = 6 ft. (55) from A.

(56) At x = 6 ft. (57) 6< x <18 (58) (59) (60)

(61)

(62) (63) (64) The maximum Bending Moment occurs at zero s earing force 1.e.x = 7.58 ft. (65)

The section BC can be more easily calculated by using a variable X measured from C. Then by a similar argument:-

(66) (67)

(68) (69) The complete diagrams are shown. It can beseen that for a uniformly varying distributed load, the Shearing Force diagram consists of a series of parabolic curves and the Bending Moment diagram is made up of "cubic" discontinuities occurring at concentrated loads or reactions. It has been shown that Shearing Forces can be obtained by integrating the loading function and Bending Moment by integrating the Shearing Force, from which it follows that the curves produced will be of a successively "higher order" in x ( See equations (6) and(7))

Appendix
Shearing Force F Mending Moment M Rate of loading w (78) (79)

INTERNAL FORCES AND MOMENTS BEAMS Axial Force, Shear Force and Bending Moment To ensure that a structural member will not fail (break or collapse) due to the forces and moments acting on it, the design engineer must know not only the external loads and reactions acting on it, but also the forces and moments acting within the member. If the beam is cut by a plane at an arbitrary cross section, either isolated part of it cannot be in equilibrium unless it is subjected to some system of forces and moments (internal forces and moments) where it joins the other part of the beam. AXIAL FORCE -the component P of internal force parallel to the beams axis - it is positive if subjects the beam to tension SHEAR FORCE - the component V of internal force normal to the beams axis - it is positive if tends to rotate the axis of the beam clockwise BENDING MOMENT - the couple M (tends to bend the beam about the axis normal to the beams axis) - it is positive if tends to bend the beams axis upward Steps for determining the internal forces and moment at a particular cross section of a beam: 1.Draw the free-body diagram and determine the reactions at supports of the beam 2.Draw the free-body diagram of the part of the beam 3.Apply the equilibrium equations to determine P, V and M Shear Force and Bending Moment Diagrams To design a beam, an engineer must know the internal forces and moments throughout its length; of special concern are the maximum and minimum values and where they occur. The shear force and bending moment diagrams are simply the graphs of V and M as functions of x. Relations Between Distributed Load, Shear Force and Bending Moment The shear force and bending moment in a beam subjected to only a distributed load w are governed by simple differential equations.

dP =0 dx

axial force does not depend on x

dV = w dx dM =V dx

- integrating this equation, we can determine V as a function of x

integrating this equation, we can determine M as a function of x

Technical Terms: absolute value-: numerical value of a real number without regard to its sign (also the modulus of a complex number). bar - : structural member designed to resist forces acting along the member axis. beam -: structural member designed to resist forces acting normal to the member axis. cantilever beam -: fixed at one end and free at the other. At the fixed end, beam can neither translate nor rotate. concentrated loads -: forces acting at a point (N, kN). couple - : a load with dimensions of force-length (N-m, kN-m). distributed loads - :forces acting over some distance (N/m, kN/m). free-body diagram -: sketch showing an object and all the forces acting on it. lateral - : perpendicular to the axis. longitudinal - : along the axis. maximum : greatest value of a function. minimum : lowest value of a function. normal - : perpendicular, makes an angle of 90 . parallel - : two or more straight lines (or planes) that do not intersect. pin-support - : restrains beam from translating horizontally and vertically but does not prevent rotation. reactions - : forces and couples at end of beams. roller-support - : translation is prevented in one direction. simply-supported beam - : pin support at one end and roller support at the other. statically determinate - : a structure is statically determinate if the reactions can be determined from equilibrium equations. uniformly distributed loads - : the load per unit length has a constant value.