UNIVERSIDAD DE CARTAGENA

PROGRAMA DE ADMINASTRACION FINANCIERA

ASIGNATURA: MATEMATICAS II
TALLER DE LIMITES DE FUNCIONES
RESUMEN DEL TEMA
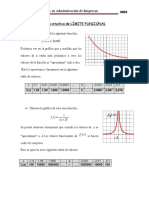
Idea intuitiva de lmite funcional.-
Observa la grfica de la siguiente funcin: ( )
x
x f 68 , 0 . 2 ) ( =
Podemos ver en la grfica que a medida que los valores de x estn ms
prximos a cero los valores de la funcin se aproximan ms a dos.
Esto lo apreciamos claramente en la siguiente tabla de valores:
x 0,1 0,0
1
0,00
1
0,000
1
.... 0 .... -
0,001
-0,01 -0,1
f(x
)
1,9
2
1,9
9
1,99
9
1,999
9

.
2

2,000
7
2,00
7
2,07
8
Observa la grfica de esta otra funcin:
( )
2 1
2
1
) (
+
=
x
x f
Se puede observar claramente que cuando los valores de x se aproximan a -2
los valores funcionales de ) (
1
x f se hacen cada vez mayores.
Esto se aprecia en la siguiente tabla de valores:

x -1,9 -1,99 -1,999 .... -2 ... -2,001 -2,01 -2,1
f
1
(x) 100 10000 1000000 . . 1000000 10000 100
Observa la grfica de esta nueva funcin:
x
x f
8
) ( =
En este caso podemos ver que a medida que los valores de x se
hacen mayores los valores funcionales se aproximan cada vez ms
a cero.
Observa la siguiente tabla de valores:
x 10 100 1000000 ....
f
1
(x) 0,8 0,08 0,000008 . 0

Por ltimo, observa la grfica de esta funcin: l l T . 2 ) ( =
En este caso, sobre la grfica se observa que a medida que los
valores de l crecen los valores de T crecen, tambin, cada vez
ms.
Sobre una tabla de valores podemos comprobar lo dicho
anteriormente:

l 10 100 1000000 ....
T 6,32 20 2000 .

Todos estos ejemplos nos llevan a poder dar una idea intuitiva del significado del concepto de lmite
funcional.
Diremos que el lmite de una funcin f es A( A puede ser cualquier nmero real o ) cuando x se
aproxima a a ( apuede ser cualquier nmero real o ) si sucede que cuanto ms se concentran los
valores de x en las proximidades de a, los valores funcionales correspondientes se concentran en las
proximidades de A.
Todo esto se escribe de modo matemtico as:
A x f lm
a x
=

) (

1. Lmite de una funcin en un punto.-
A) LMITES LATERALES FINITOS.
A
1
) Lmite por la izquierda:
Se dice que A x f
lm
a x
=

) ( si cuando x toma valores prximos a a, por su izquierda, ) (x f

toma valores cada vez ms prximos al nmero A.
A
2
) Lmite por la derecha:
Se dice que A x f
lm
a x
=
+

) ( si cuando x toma valores prximos a a, por su derecha, ) (x f

toma valores cada vez ms prximos al nmero A.
Ejemplo.-

Observa sobre el grfico de esta funcin como se cumple que:
0 ) (
2
=

x f
lm
x

3 ) (
2
=
+

x f
lm
x


Fjate ahora en este otro ejemplo:

La funcin que tiene esta grfica cumple que:
0 ) (
1
=

x f
lm
x

0 ) (
1
=
+

x f
lm
x


En el primer caso los lmites laterales en el valor de x =2 son distintos, mientras que en el segundo ejemplo
los lmites laterales en el valor de x = 1 coinciden (valen cero).
Se dice entonces que si los lmites laterales toman el mismo valor, es decir, A x f
lm
a x
=

) ( y
A x f
lm
a x
=
+

) ( existe el lmite de ) (x f en a x = , se escribe:

A x f
lm
a x
=

) (
Si los lmites laterales toman distinto valor en a x = se dice que no existe el lmite de ) (x f en a x = .
B) LMITES LATERALES NO FINITOS.
B
1
) Lmite por la izquierda:
Se dice que + =

) (x f
lm
a x
si cuando x toma valores prximos a a, por su izquierda, ) (x f
toma valores cada vez mayores, llegando a superar a cualquier valor, por muy grande que ste sea.
B
2
) Lmite por la derecha:
Se dice que + =
+

) (x f
lm
a x
si cuando x toma valores prximos a a, por su derecha, ) (x f
toma valores cada vez mayores, llegando a superar a cualquier valor, por muy grande que ste sea.
Ejemplo.-
En esta grfica de la funcin ) (
1
x f vemos que se verifica:
+ =

) (
1
2
x f
lm
x

+ =
+

) (
1
2
x f
lm
x


B
3
) Lmite por la izquierda:
Se dice que =

) (x f
lm
a x
si cuando x toma valores prximos a a, por su izquierda, ) (x f
toma valores cada vez ms negativos(o sea, ms pequeos).
B
4
) Lmite por la derecha:
Se dice que =
+

) (x f
lm
a x
si cuando x toma valores prximos a a, por su derecha, ) (x f
toma valores cada vez ms negativos(o sea, ms pequeos).
Ejemplo.-
En esta grfica de la funcin ) (x f vemos que se verifica:
=

) (
0
x f
lm
x
, =
+

) (
0
x f
lm
x

Si + =

) (x f
lm
a x
y + =
+

) (x f
lm
a x
entonces: + =

) (x f
lm
a x

Si =

) (x f
lm
a x
y =
+

) (x f
lm
a x
entonces =

) (x f
lm
a x


Si los lmites laterales toman distinto valor en a x = se dice que no existe el lmite de ) (x f en a x = .

C) PROPIEDADES DE LOS LMITES.
C
1
) ) ( ) ( )) ( ) ( ( x g x f x g x f
lm lm lm
a x a x a x
=
Siempre que no aparezca la indeterminacin:
C
2
) ) ( ). ( )) ( ). ( ( x g x f x g x f
lm lm lm
a x a x a x
=
Siempre que no aparezca la indeterminacin: . 0
C
3
)
) (
) (
)
) (
) (
(
x g
x f
x g
x f
lm
lm
lm
a x
a x
a x

= con 0 )) ( ( =

x g
lm
a x

Siempre que no aparezcan las indeterminaciones:

o
0
0

C
4
)
) (
) (
) ( ) ) ( (
x g
a x
x g
a x
lm
a x
x f x f
lm lm


=
con 0 ) ( > x f
(*La funcin potencia solo est definida para valores positivos de la base)
Siempre que no aparezcan las indeterminaciones:

1 , 0 ,
0 0


2. Lmites en el infinito.-

A) LMITE FINITO.
Se dice que A x f
lm
x
=
+
)) ( ( si al aumentar los valores de x tanto como queramos los valores
de la funcin ) (x f se concentran en las proximidades de A.
Se dice que A x f
lm
x
=

)) ( ( si al hacer los valores de x tan negativos como queramos los
valores de la funcin ) (x f se concentran en las proximidades de A.
Se dice que )) ( ( x f
lm
x
no existe, si al aumentar (o disminuir) los valores de x cada vez ms
(cada vez ms pequeos) los valores de ) (x f ni crecen ni decrecen ni se acercan, cada vez ms, a ningn
nmero.


Ejemplo.-







B) LMITE NO FINITO.


Se dice que + =
+
)) ( ( x f
lm
x
si al aumentar los valores de x tanto como queramos los valores
de la funcin ) (x f son cada vez ms grandes.
Se dice que =
+
)) ( ( x f
lm
x
si al aumentar los valores de x tanto como queramos los valores
de la funcin ) (x f son cada vez ms negativos.
Se dice que + =

)) ( ( x f
lm
x
si al hacerse ms negativos los valores de x los valores de la
funcin ) (x f se hacen cada vez ms grandes.
Se dice que =

)) ( ( x f
lm
x
si al hacerse ms negativos los valores de x los valores de la
funcin ) (x f se hacen cada vez ms negativos.

Todo lo referente a las propiedades de los lmites de una funcin en un punto se cumple tambin en el caso
de lmites en el infinito. Es decir, todas las propiedades vistas en el apartado anterior se cumplen ahora
poniendo en lugar de a,
Ejemplo.-
Observa sobre la grfica de la funcin
1
f que se cumple:
=
+
)) ( (
1
x f
lm
x


En la grfica de
3
f puedes ver que se cumple:
+ =
+
)) ( (
3
x f
lm
x


Dibuja t la grfica de una funcin que modelice los lmites:
+ =

)) ( ( x f
lm
x
y =

)) ( ( x f
lm
x

Observacin.- Al calcular este tipo de lmites en el infinito puede que obtengamos una indeterminacin (en
apariencia), que no lo es en realidad.


Comparacin de infinitos
Si tenemos que =

)) ( ( x f
lm
x
y =

)) ( ( x g
lm
x

Se dice que f es un infinito de orden superior a g si se verifica:
( )
( )
=
|
|
.
|

\
|

x g
x f
lm
x
o lo que es lo mismo:
( )
( )
0 =
|
|
.
|

\
|

x f
x g
lm
x


Es fcil comprobar las siguientes afirmaciones:
- Dadas dos potencias de x, la de mayor exponente es un infinito de orden superior:
+ =
|
|
.
|

\
|

x
x
lm
x
2
3
+ = =
|
|
.
|

\
|
+ +
1
2
3
2 3
7 7 x
x
x
x
lm lm
x x

- Dadas dos funciones exponenciales de bases mayores que 1(el lmite cuando + x de estas
funciones es un infinito pues cuando x se dice un infinitsimo), la de mayor base es un
infinito de orden superior.
( )
+ =
|
|
.
|

\
|
+
x
x
x
lm
5 , 1
2

- Cualquier funcin exponencial de base mayor que 1 es un infinito de orden superior a cualquier
potencia: + =
|
|
.
|

\
|
+
50
5000
2
x
x
x
lm

- Tanto las funciones exponenciales de base mayor que 1 como las potencias de x son infinitos de
orden superior a cualquier funcin logartmica:
( )
+ =
|
|
.
|

\
|
+
x
x
x
lm
ln
5 , 1
+ =
|
.
|

\
|
+
x
x
lm
x
ln

- Dos polinomios del mismo grado o dos potencias de la misma base son infinitos del mismo orden,
es decir:
( )
( )
0 = =
|
|
.
|

\
|

l
x g
x f
lm
x

0 4
2
8
1 5 2
8 2 8
3
2 3
= = =
|
|
.
|

\
|
+
+

x x
x x
lm
x
0
5
1
52
2
= =
|
|
.
|

\
|
+
x
x
x
lm


Familiarzate con estos sencillos resultados pues son muy tiles para el clculo de lmites.
3. Ramas infinitas. Asntotas de una curva.-
Al desarrollar el tema nos hemos encontrado en alguna ocasin tramos de una curva que se alejan
indefinidamente, son las llamadas Ramas infinitas.
Cuando una Rama infinita se cie (se aproxima) a una recta, a esta recta se la llama Asntota de la curva y a
la rama correspondiente se le llama:
Rama asinttica.
A) Rama infinita en x=a. Asntota Vertical.
Las nicas ramas infinitas que se pueden encontrar en valores concretos de la abscisa ) ( a x = son
las ramas asintticas verticales.
As, si una funcin ) (x f verifica que =

) (x f
lm
a x
decimos que ) ( a x = es una Asntota
Vertical de dicha funcin.
La posicin de la curva respecto a la asntota depende del signo de los lmites laterales.
Ejemplo.-
Las Asntotas verticales de la funcin
x x
x
x f
2
2
) (
2
2

+
= son: 2 0 = = x y x
Posicin

0 x
+
0 x

2 x
+
2 x
x -0,01 0,01 1,99 2,01
) (x f
positiva negativa negativa positiva
resulta
+ =

) (
0
x f
lm
x

=
+

) (
0
x f
lm
x

=

) (
2
x f
lm
x

+ =
+

) (
2
x f
lm
x


0 = x + =

) (
0
x f
lm
x
=
+

) (
0
x f
lm
x

2 = x =

) (
2
x f
lm
x
+ =
+

) (
2
x f
lm
x



Ejemplo.-
Observa la grfica de la funcin e indica si tiene Asntota Vertical:

En este caso la funcin presenta una Asntota vertical ) 0 ( = x
Porque se verifica que: =

) (
0
x f
lm
x
y =
+

) (
0
x f
lm
x

En consecuencia: =

) (
0
x f
lm
x

B) Ramas infinitas cuando x .
Asntota Horizontal. Asntota oblicua. Rama Parablica.
Hay varios tipos de ramas infinitas cuando x :
B
1
) Asntota Horizontal.- Si se verifica que A x f
lm
x
=

)) ( ( decimos entonces que la recta de
ecuacin A y = es Asntota Horizontal de la funcin.
La posicin de la curva respecto a la asntota depende del signo de A x f ) ( .
Ejemplo.-
La funcin
3
2

=
x
x
y tiene una Asntota Horizontal 2 = y , se cumple que: 2 )) ( ( =
+
x f
lm
x
y
2 )) ( ( =

x f
lm
x
, la posicin de la curva respecto a la Asntota la determina el signo de la diferencia
entre los valores:

+

=

=
asntota debajo f negativo x
asntota encima f positivo x
x x
x
A x f
3
6
2
3
2
) (


(Tiene adems una Asntota vertical en 3 = x )
Ejemplo.-
La funcin cuya grfica es la dada ms abajo, tiene una Asntota horizontal 0 = y

Se cumple que 0 )) ( ( =

x f
lm
x

Evidentemente la grfica muestra que la funcin est por encima de la Asntota para
los valores de x
Ejemplo.-
La funcin cuya grfica es la de ) (
2
x f , tiene Asntota horizontal 3 = y

Se cumple que 3 )) ( (
2
=
+
x f
lm
x

Evidentemente la grfica muestra que la funcin est por debajo de la Asntota
para los valores de + x


B
2
) Asntota Oblicua.- Hay funciones ) (x f que al hacer que + x (o que ) ( x ) se
aproximan mucho a una recta de ecuacin
0 = + = m n mx y cindose a ella. Dicha recta se dice Asntota Oblicua para esa funcin.
Para que dicha recta sea Asntota Oblicua de ) (x f se ha de cumplir
( ) mx x f n c
x
x f
m b x f a
lm lm lm
x x x
= = = =

) ( ) 0
) (
) ) ( )
La posicin de la curva respecto a la asntota depende del signo de ( ) n mx x f + ) ( .
Ejemplo.-
La funcin
1
1 3
2

+
=
x
x x
y tiene una Asntota Oblicua 2 = x y
2
1
1 2
. 1
1
1 3
)
1
1 3
1
1 3
)
1
1 3
1
1 3
)
2
2
2
2
2
2
=
|
.
|

\
|

+
= |
.
|

\
|

+
=
=

+
=

+
=

+
+ =

+



+
x
x
x
x
x x
n c
x x
x x
x
x
x x
m b
x
x x
x
x x
a
lm lm
lm
lm
lm
x x
x
x
x



Ejemplo
.-
La
funcin
x x
x
y
2
2
3

= tiene una Asntota oblicua.

Asntota Oblicua: 2 + = x y
Haz t los clculos como en el ejemplo anterior:

X 50 100 1000
1
1 3
) (
2

+
=
x
x x
x f

47,98

97,99

997,999

2 = x y
48 98 998
DIFERENCIA 0,02 0,01 0,001 0


B
3
) Ramas Parablicas.- Si se cumple =

) (x f
lm
x
y la curva no tiene Asntota Oblicua
entonces la curva presenta una Rama Parablica. Hay dos tipos:

1. Tipo 1.- La curva crece, o decrece, cada vez ms deprisa. De este tipo son las ramas
parablicas de las funciones polinmicas y exponenciales.
2. Tipo 2.- La curva crece, o decrece, cada vez ms despacio. De este tipo son las ramas
parablicas de las funciones radicales y logartmicas.
Ejemplo.-
La funcin 1 ) ( + = x x f tiene una Rama parablica tipo 2

La funcin crece cada vez ms despacio.

+ =
+
) (x f
lm
x



Ejemplo.-
La funcin
x
y ) 68 , 0 .( 2 = tiene una Rama parablica tipo 1
La funcin decrece cada vez ms rpido.

+ =

) (x f
lm
x



Ejemplo.-
Dadas las funciones: x y
3
log = y
x
y 3 = . Determina sus ramas parablicas.











4. Calculo de Lmites. El nmero e.-
A) INDETERMINACIN
En la mayora de los casos basta con efectuar las operaciones indicadas.
Ejemplo.-
Calcula el siguiente lmite: |
.
|

\
|

+
1 1
1
2
2
1 x
x
x
x
lm
x
indeterminacin
Para resolverla efectuamos la operacin indicada entre parntesis:
|
.
|

\
|

+
= |
.
|

\
|

+ +
= |
.
|

\
|

+ +
= |
.
|

\
|

+
1
1 2
1
1 2
1
) 1 ).( 1 (
1 1
1
2 2
2 2
2
2
2
2
x
x
x
x x x
x
x x x
x
x
x
x


Por tanto se cumple que: |
.
|

\
|

+
1 1
1
2
2
1 x
x
x
x
lm
x
=

+
=
|
.
|

\
|

1
1
1
1 2
2
1
x si
x si
x
x
lm
x



Observa la grfica de:
1
1 2
) (
2

+
=
x
x
x f








En otros casos, sobre todo aquellos en que aparecen radicales, basta multiplicar y dividir por la
expresin radical conjugada.
Ejemplo.
Calcula el siguiente lmite: ( ) x x
lm
x


indeterminacin
Para resolverla multiplicamos y dividimos la expresin dada por su conjugada.
( ) x x
lm
x


=
) (
) ).( (
x x
x x x x
lm
x
+
+

= + =
+

x x
x x
lm
x
2

Evidentemente el ltimo lmite es ms infinito pues crece ms rpidamente el numerador que el
denominador.
-9 -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8 9
x
y


B) INDETERMINACIN . 0
En la mayora de los casos basta con efectuar las operaciones indicadas.
Ejemplo.-
Calcula el siguiente lmite: |
.
|

\
| +

2
2
0
1
.
1 x
x
x
x
lm
x
indeterminacin . 0
Para resolverla efectuamos la operacin indicada entre parntesis:
|
.
|

\
|

+
=
|
|
.
|

\
|

+
= |
.
|

\
| +
1
1
). 1 (
) 1 .( 1
.
1
2
2
2
2
x
x
x x
x x
x
x
x
x
y en consecuencia:
|
.
|

\
| +

2
2
0
1
.
1 x
x
x
x
lm
x
= 1
1
1
0
=
|
.
|

\
|

+
x
x
lm
x

C) INDETERMINACIN
0
0

Cuando solamente aparecen funciones racionales basta con descomponer factorialmente
numerador y denominador.

Ejemplo.-
Calcula el siguiente lmite: |
.
|

\
|
+
+
10 3
6 5
2
2
2 x x
x x
lm
x
indeterminacin
0
0

Para resolverla descomponemos factorialmente numerador y denominador.
( )( )
( )( ) 5
3
2 . 5
2 . 3
10 3
6 5
2
2
+

=
+

= |
.
|

\
|
+
+
x
x
x x
x x
x x
x x
en consecuencia:
|
.
|

\
|
+
+
10 3
6 5
2
2
2 x x
x x
lm
x
=
7
1
5
3
2

=
|
.
|

\
|
+

x
x
lm
x


En aquellos casos en los que aparecen radicales, basta con multiplicar y dividir por la expresin radical
conjugada.
Ejemplo.-
Calcula el siguiente lmite:
x
x
lm
x

1
1
1
indeterminacin
0
0

Para resolverla multiplicamos numerador y denominador por x + 1 .
x
x
lm
x

1
1
1
=
( )( )
( )( ) x x
x x
lm
x
+
+

1 . 1
1 . 1
1
=
( )( )
( ) x
x x
lm
x
+
1
1 . 1
1
=
( ) 2 1 1 1
1
= =

x
lm
x




D) INDETERMINACIN

En la mayora de los casos basta con dividir numerador y denominador por la mayor potencia de x
del denominador.
Ejemplo.-
Calcula el siguiente lmite:
1
1 4
2
2
+
+
+ x
x x
lm
x
indeterminacin

Para resolverla dividimos numerador y denominador por
2
x
1
1 4
2
2
+
+
+ x
x x
lm
x
=
2
2
2
2
1
1 4
x
x
x
x x
lm
x +
+
+
=
2
2
1
1
1 1
4
x
x x
lm
x
+
+
+
= 4
1
4
=
Ejemplo.-
Calcula el siguiente lmite:
x
x x
lm
x
+
+
2
indeterminacin

Para resolverla dividimos numerador y denominador por x
x
x x
lm
x
+
+
2
=
x
x
x
x x
lm
x
+
+
2
=
x
x
x
x x
lm
x
2
2
+
+
=
1
1
1
x
lm
x
+
+
= 1
1
1
=
Observa la siguiente grfica:

Grfica de:
x
x x
x f
+
=
2
) (

1 : . .
1 ) (
=
+
y H A
x f x


1 : . .
1 ) (
=

y H A
x f x

-4 -3 -2 -1 1 2 3 4
-4
-3
-2
-1
1
2
3
4
x
y
Observa que en el caso de que x el lmite:
1
2
=
+
x
x x
lm
x
se obtendra dividiendo
numerador y denominador por: x
(Dentro de una raz cuadrada el nmero ha de ser positivo) y as se explica que ese lmite valga -1.

E) INDETERMINACINES:
0 0
, 0 , 1

Para resolver este tipo de indeterminaciones usaremos la denominada
Regla de Lhpital basada en las derivadas y que veremos ms adelante.

De todas formas (si la indeterminacin es

1 ) hay una frmula de resolucin para esa indeterminacin de

uso muy frecuente basada en el nmero e. Vemosla, pero primeramente recordemos que:
La sucesin numrica definida por
n
n
n
a
|
.
|

\
|
+ =
1
1 tiene lmite finito cuyo valor es un nmero irracional
que se representa por la letra ( e).
Aproximadamente este nmero vale: ........ 718281 , 2 = e
Veamos ahora distintos lmites relacionados con el nmero e que nos van a permitir establecer la frmula
de resolucin de las indeterminaciones:

1
A)



(siendo
n
o cualquier sucesin con ( ) 0 =
+
n
n
lm
o )
En efecto, hagamos
n
n
1
= o tenemos que ( ) 0 =
+
n
n
lm
o y + =
n
n
o
1

Sustituyendo en A) ( ) e
n
n
n
n lm lm
n
n
=
|
.
|

\
|
+ = +
+
1
1 1
1
0
o
o
o
B)
1
1 1
1

+
= =
|
.
|

\
|
e
e n
n
n
lm

Si hacemos
n
n
1
= o tendremos que: ( ) 0 =
+
n
n
lm
o y
n
n
o
1
=
( ) ( )
e
e
n
n
n
n
n
n n
n
n
lm lm lm
1
1 1
1
1
1
1
1
0
1
0
= =
(
(

+ =
(

+ =
|
.
|

\
|

+
o
o
o
o
o o

C)
x
n
n
e
n
x
lm
=
|
.
|

\
|
+
+
1
Si hacemos
n
x
n
= o tendremos que: ( ) 0 =
+
n
n
lm
o y
n
x
n
o
=
( ) ( )
x
x
n
x
n
n
n
e
n
x
n
n
n
n
lm lm lm
=
(
(

+ =
(

+ =
|
.
|

\
|
+
+
o
o
o
o
o o
1
0 0
1 1 1
D)
( )
( ) e
n
n
lm
n
log
1 log
0
=
+

o
o
o
. En efecto:
( )
( ) ( ) ( ) ( ) e n
n
n
n n
n n
n
n
lm lm lm
log 1 log 1 log
1 log 1
0
1
0 0
=
(
(

+ =
(

+ =
+

o
o
o
o o
o o
o
o

E) Sean
n
o y
n
| dos sucesiones tales que: ( ) 1 =
+
n
n
lm
o y ( ) =
+
n
n
lm
|
En este caso tendremos la indeterminacin: ( )

+
=1
n
n
n
lm
|
o
Se verifica la siguiente igualdad de lmites:

( )
( ) | | 1
+

=
n n
n n
lm
e
n
n
lm
o |
|
o

Como: ( ) 0 1 =

n
n
lm
o ( ) ( )
( ) 1
1
1
1 1

+ =
n n
n
n
n n
o |
o
|
o o y A)

( ) ( )
( ) ( ) 1 1
1
1
1 1

=
(

+ =
n n
n
n n
n
n
lm
e
n
n
n
n
lm lm
o | o |
o
|
o o
Ejemplo.-
Calcula el lmite:
3 2
1
2
+
+
|
.
|

\
|
+
+
x
x x
x
lm
tenemos una indeterminacin

1
Aplicamos pues la frmula dada ms arriba y tenemos que:
3 2
1
2
+
+
|
.
|

\
|
+
+
x
x x
x
lm
=
( ) |
.
|

\
|

+
+
+
+
1
1
2
. 3 2
x
x
x
lm
x
e
=
4
1
6 4
e e
x
x
lm
x
=
+
+
+


Calcula t como ejercicio el lmite siguiente del mismo modo:
4 2
2
3
+
+
|
.
|

\
|
+
+
x
x x
x
lm
Solucin:
2
e

5. Funcin continua en un punto y en un Intervalo.-
La idea de funcin continua es, como ya sabemos, la de aquella cuya grfica puede ser construida
con un solo trazo.
Al trabajar con la expresin analtica de la funcin, veremos que el concepto de lmite es
fundamental para el estudio de la continuidad, de tal modo que estableceremos un criterio, basado en el
lmite, para determinar cuando una funcin es o no continua.

Ejemplo.-
Observa las grficas de distintas funciones:

Esta funcin tiene por expresin analtica:

>
s s
<
=
5 11 2
5 0 4
0 4
) (
x si x
x si x
x si
x f
Observa su trazo continuo en todo 9


Esta otra funcin tiene por expresin analtica:

>
< +
=
1
2
1 3
) (
x si
x
x si x
x f
Observa su trazo continuo en su dominio
) , 3 [ + = D

En estos dos primeros casos las funciones dadas son ambas de trazo continuo, pero hay otros casos en los
que las funciones tienen una grfica que no puede ser dibujada con un nico trazo. Veamos distintos casos:

Esta funcin tiene por expresin analtica:

> +
< s
<
=
3 2
3 0 2
0
) (
2
x si x
x si x
x si x
x f
Observa su trazo no continuo en el valor de x=3

En los dems puntos de su dominio su trazo es continuo
Observa las grficas de distintas funciones que no tienen un nico trazo y por tanto no son continuas:






Veamos pues ahora cual es la formalizacin matemtica del concepto de continuidad.
Diremos que una funcin de expresin analtica ) (x f y = es continua en un punto de su dominio
a x = si se verifican estas condiciones:

) ( ) ( )
) ( )
) ( )
a f x f c
x f Existe b
a f Existe a
lm
lm
a x
a x


Observacin 1: la palabra existe de la condicin a) quiere decir que el resultado sea un nmero real
Observacin 2: la condicin c) basta para definir la continuidad en un punto de la funcin dada pues si esta
condicin c) se verifica, necesariamente se han de dar a) y b).
Observacin 3: cuando una funcin no es continua en un punto se dice discontinua
Diremos que una funcin ) (x f y = es continua en un intervalo abierto ( ) b a, si es continua en todos y
cada uno de los puntos de dicho intervalo.

Diremos que una funcin ) (x f y = es continua por la derecha en un punto de su dominio a x = si se
cumple ) ( ) ( a f x f
lm
a x
=
+

Diremos que una funcin ) (x f y = es continua por la izquierda en un punto de su dominio a x = si se
cumple ) ( ) ( a f x f
lm
a x
=

Diremos que una funcin ) (x f y = es continua en un intervalo cerrado | | b a, si:
1. ) (x f y = es continua en el intervalo abierto ( ) b a,
2. ) (x f y = es continua por la derecha en a x =
3. ) (x f y = es continua por la izquierda en b x =

Es conveniente sealar aqu que todas las funciones definidas por expresiones analticas elementales
(lineales, cuadrticas, de proporcionalidad inversa, radicales, logartmicas, exponenciales, trigonomtricas)
son todas continuas en los puntos en los que estn definidas (o sea, en su dominio).

PROPIEDADES DE LAS FUNCIONES CONTINUAS.
Sean ) (x f y ) (x g dos funciones continuas en a x = se tiene entonces que:
1. ) ( ) ( x g x f es continua en a x =
2. ) ( ). ( x g x f es continua en a x =
3.
) (
) (
x g
x f
es continua en a x =
4.
) (
) (
x g
x f es continua en a x = ( suponiendo 0 ) ( > a f )

Tipos de Discontinuidad de las Funciones.-
Ya hemos sealado anteriormente que una funcin es Discontinua en un punto a x = cuando no cumple
alguna de las tres condiciones de continuidad en ese punto.
De ah que podamos establecer distintos tipos de Discontinuidad:

1. Evitable.- Cuando existe el ) (x f
lm
a x
pero no coincide con el valor de ) (a f ,por una de estas
dos razones, son distintos los valores o no existe ) (a f
Ejemplo.-

(En este caso el punto es: 1 = a )
El valor de la funcin en el punto es: 4 ) 1 ( = f
El valor del lmite en ese punto es: 2 ) (
1
=

x f
lm
x

En este caso son distintos los valores.


(En este caso el punto es: 2 = a )
El valor de la funcin en el punto ) 2 ( f No existe
El valor del lmite en ese punto es 3 ) (
2
=

x f
lm
x

En este caso no existe ) 2 ( f



2. De Salto.- Cuando existe el lmite por la derecha y por la izquierda (siendo ambos finitos) pero no
coinciden.
Ejemplo.-
6 ) (
3
=

x f
lm
x
y 5 ) (
3
=
+

x f
lm
x

En este caso los lmites laterales no coinciden siendo ambos finitos.
1 6 5 ) ( ) ( = = =
+

x f x f Salto
lm lm
a x a x



3. Asinttica.-Alguno de los lmites laterales(o ambos) no es finito.
Ejemplo.-

Para esta funcin los lmites laterales en 1 = x son ambos no finitos, de
hecho:
+ =

) (
1
x f
lm
x
=
+

) (
1
x f
lm
x



4. Esencial.- Cuando no existe alguno (o ambos) de los lmites laterales
Ejemplo.- Observa la grfica de la siguiente funcin:

>
<
|
.
|

\
|
=
0 ) sin(
0
1
sin
) (
x si x
x si
x x f ) (
0
x f
lm
x

No hay; 0 ) (
0
=
+

x f
lm
x











6. Teoremas relacionados con la continuidad de las funciones.
Muchas de las propiedades de las funciones continuas las acepta como evidentes nuestro sentido comn,
sobre todo cuando las interpretamos geomtricamente mediante la representacin grfica.
Sin embargo, el rigor matemtico, en aras a evitar errores y paradojas, exige elaborar demostraciones de
estas propiedades apoyndose en definiciones precisas de los conceptos bsicos.
Teorema de conservacin del signo.-
Si la funcin f es continua en
0
x y ( ) 0
0
= x f existe un entorno de
0
x en el que ( ) x f toma el
mismo signo que ( )
0
x f
Explicacin.- Si una funcin f es continua en
0
x las imgenes de los puntos cercanos a
0
x no se separan
mucho de ( )
0
x f por lo que tendrn el mismo signo que esta ltima.

Interpretacin grfica.-
-2 -1 1 2
x
y

Cuando f es
continua en
0
x
siempre hay algn
entorno de
0
x en
el que la funcin
mantenga el signo
de ( )
0
x f .
Ejemplo:la funcin no es continua en
0
x y no hay ningn entorno
de
0
x en el que la funcin conserve el signo.
Teorema de Bolzano (o teorema de los ceros).-
Si la funcin f es continua en el intervalo | | b a, y toma
distinto signo en los extremos del mismo, entonces se anula en algn punto | | b a c , e
O sea hay al menos un valor | | b a c , e en el que ( ) 0 = c f

Explicacin.- La grfica de una funcin continua no tiene agujeros ni interrupciones, y si atraviesa una
lnea recta, forzosamente tendr un punto comn con ella.
Interpretacin grfica.-

La grfica de la funcin necesariamente ha de atravesar al eje X al pasar del semiplano inferior al semiplano
superior, y por lo tanto ( ) x f se anular
al menos en un punto (en este caso concreto en tres).


Aunque la funcin cambie de signo en los extremos de
| | b a, , observa que si no es continua en dicho intervalo
(en el ejemplo es discontinua en | | b a x ,
0
e ) puede
que no se anule en ningn punto de ese intervalo (como en
la del ejemplo).





Teorema de Darboux (o teorema de los valores intermedios).-
Si la funcin f es continua en el intervalo | | b a, y k es un nmero comprendido entre ( ) a f y
( ) b f , o sea ( ) ( ) b f k a f < < , entonces existe algn punto ( ) b a c , e tal que ( ) k c f =
Explicacin.-Es una consecuencia inmediata del teorema de Bolzano.
La grfica de una funcin continua f en el intervalo | | b a, atravesar cualquier recta horizontal situada
entre ( ) a f y ( ) b f . Por lo tanto, la funcin tomar dentro del intervalo ( ) b a, cualquier valor
comprendido entre ( ) a f y ( ) b f .
Interpretacin grfica.-

Intenta demostrar este teorema como consecuencia directa del de
Bolzano:
Aplica Bolzano a la funcin ( ) ( ) k x f x g = !









Otra consecuencia inmediata del teorema de Bolzano es.
f y g son dos funciones continuas en | | b a, y ( ) ( ) a g a f < y ( ) ( ) b g b f > entonces existe
un numero ( ) b a c , e tal que ( ) ( ) c g c f =

Aplica Bolzano a la funcin ( ) ( ) ( ) x g x f x h = !









Teorema de Weierstrass.-
Si f es una funcin continua en el intervalo | | b a, entonces tiene un mximo y un mnimo absolutos en
ese intervalo. Es decir, existen dos nmeros c y d de dicho intervalo para los que se verifica:
| | ( ) ( ) ( ) d f x f c f cumple b a x cualquier s s e ,


En la funcin f del grfico, observa como el mximo
o el mnimo pueden alcanzarse, bien en un extremo,
bien en un punto interior del intervalo.
As en este ejemplo el mnimo se alcanza en a y el
mximo en c.



Observa que si el intervalo fuese abierto no podramos asegurar la existencia de mximo o mnimo en el
intervalo. En el ejemplo anterior,
f no tendra mnimo en el intervalo ( ) b a, ya que ( ) b a a , e .

Si f no fuese continua en | | b a, , en el siguiente ejemplo es discontinua en c
, no estara garantizada la existencia de mximo o mnimo en dicho intervalo pues
la funcin podra no estar acotada
(como en el ejemplo) en dicho
intervalo.
















Programa de Administracin de Financiera
Taller de Lmites
1. Calcula los siguientes lmites:


2. Calcular:




3. De la siguiente funcin se pide:

4. Estudiar si existe algn valor de k que haga continua a las siguientes funciones:

5. Estudiar la continuidad de las siguientes funciones:




6. Representar la siguiente funcin y razonar si es continua en los puntos que se indican: