Professional Documents
Culture Documents
Probability Distribution
Uploaded by
Tee Pei LengOriginal Description:
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Probability Distribution
Uploaded by
Tee Pei LengCopyright:
Available Formats
edmet-nklpunya.blogspot.
com
Additional Mathematics
Modules
Form 5
(Version 2012)
My
Topic: 20
DISTINCTION
in
by
NgKL
edmet-nklpunya.blogspot.com
20.1 BINOMIAL DISTRIBUTION
Important Notes
edmet-nklpunya.blogspot.com
Exercise 20.1.1
Determine the Probability by Binomial Distributions
P(X = r ) = n Cr p r q n - r
1. Madonna has bought 6 chicken eggs from a sundry shop. The probability of getting rotten eggs from a sundry shop is 0.2. Find the probability that (a) only one egg is rotten. (b) all the eggs are not rotten.
2. The probability that Jacob will win in a BSMM competition is . If he participates in 5 events, calculate the probability that he will win (a) exactly 3 events, (b) at least 4 events.
3. The probability that Michael Jackson will be late to school is 0.15. Find the probability that in 5 days, the student will be late for (a) exactly 2 days, (b) not more than 1 day.
4. The probability that Tall Chen hits a target in an archery competition is 0.6. If she attempts 8 times, calculate the probability that she will hit the target (a) exactly 7 times, (b) at least 7 times.
5. In a certain region, the probability that it will rain on a day is 0.25. Calculate the probability that in a period of one week, it rains on (a) exactly 3 days, (b) less than 3 days.
6. It is known from a study that 70% of a type of seed will germinate. If Mama Jeeva has planted 10 seeds in her garden, find the probability that (a) exactly five seeds will germinate, (b) at least 8 seeds will germinate.
edmet-nklpunya.blogspot.com
Exercise 20.1.1
Determine the Probability by Binomial Distributions
P(X = r ) = n Cr p r q n - r
7. Purple Chen walks to school everyday. The probability that he will be late to school on any one day is 0.2. Find the probability that Purple Chen will be late on (a) only two days, (b) more than 1 days.
8. Parkson Arwin will takes 10 subjects in the SPM examination. The probability that he will pass any one of the subjects is 0.7. Find the probability that Parkson Arwin will pass (a) all the 10 subjects, (b) at least 2 subjects.
9. The probability that a student will doze off during a lesson is 0.15. Find the number of students that must be chosen so that the probability of finding at least one student doze off during a lesson exceed 99%.
10. 25% of the teachers of a school have more than 2 children (a) If 4 teachers are chosen at random from the school, find the probability that only 3 teachers have more than 2 children. (b) Find the maximum number of teachers that must be chosen at random such that the chances of at least one teacher in the school having more than 2 children exceeds 90%
edmet-nklpunya.blogspot.com
Exercise 20.1.2
Plot the Graph of Binomial Distributions
1. In a chess competition, a player has to play 3 games. The probability a player to win is 0.6. Plot the graph of the binomial distribution.
2. The probability of David hitting the target in shooting competition is 0.45. Plot the graph of binomial distribution if David fires four shots.
edmet-nklpunya.blogspot.com
Exercise 20.1.3
Mean, = np
Variance, 2 = npq
Std. Dev., =
npq
Determine the Mean, the Variance and the Standard Deviation of Binomial Distribution
1. A fair dice is rolled 10 times continuously. The probability of obtaining the number 6 is . Find the mean, the variance and the standard deviation.
1 5
2. The probability that a bomb which is released by a jet fighter to hit its target is 0.8. If 40 bombs are released by the jet fighter, determine the mean, the variance and the standard deviation.
3. In a class of 32 students, 80% of them passed an Additional Mathematics test. Find the mean, the variance and the standard deviation of the result of the test.
4. In an objective test, four options of answers are given to a candidate to choose from. If the test consists of 40 questions, find the mean, the variance and the standard deviation of the test.
5. In the qualifying test for entrance to a university, 48 candidates pass the test and the variance is 46.08. Find the number of candidate who sit for the test. Hence, determine the probability of a candidate passing the test.
6. Given that three out of ten students in a school have been selected to participate in a national service program. If there are 270 students involved in the program, determine the number of students in the school. Hence find its standard deviation.
edmet-nklpunya.blogspot.com
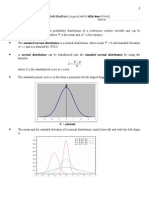
20. 2 NORMAL DISTRIBUTION
Important Notes
edmet-nklpunya.blogspot.com
Exercise 20.2.1 Sketch the Standard Normal Distribution Curve and Determine the Value of Probability 1. P(Z > 1.543)
f(z)
2. P(Z < 0.852)
f(z)
z 0 0
3. P(Z > 1.022)
f(z)
4. P(Z 0.839)
f(z)
z 0 0
5. P(Z 0.35)
f(z)
6. P(Z 0.635)
f(z)
z 0 0
7. P(0.75 < Z < 1.2)
f(z)
8. P(0.5 < Z < 1.75)
f(z)
z 0 0
9. P(1.25 < Z < 0.6)
f(z)
10. P(0 < Z < 1.228)
f(z)
z 0 0
11. P(Z 0.35)
12. P(0.5 < Z < 1.25)
13. P(Z < 0.6)
14. P(1.25 < Z < 0.6)
edmet-nklpunya.blogspot.com
Exercise 20.2.2 Sketch the Standard Normal Distribution Curve and Determine the z-value or k-value 1. P(Z > z) = 0.0883 0 2. P(Z < z) = 0.1401 0
3. P(Z > k ) = 0.2327 0
4. P(Z < k ) = 0.825) 0
5. P(Z > z ) = 0.75) 0
6. P(Z < z) = 0.5377 0
7. P(k < Z < 0) = 0.342 0
8. P(0 < Z < k) = 0.358 0
9. P(z < Z < 0.75) = 0.6 0
10. P(0.5 < Z < z) = 0.54 0
11. P(Z > z) = 0.25
12. P(2.21 < Z < k) = 0.9861
13. P(Z < k ) = 0.00641
14. P( z < Z < 0.65) = 0.2526
edmet-nklpunya.blogspot.com
10
Exercise 20.2.3 Determine the z-value from a random chosen data and the probability 1. The masses of students in a school are normally distributed with a mean of 52 kg and a standard deviation of 2.5 kg. (a) Find the z-value the mass of a student chosen at random has a mass of more than 50 kg. (b) Hence find the probability of chosen such a student
z=
2. The height of students in a school are normally distributed with a mean of 160 cm and variance of 144 cm2. (a) Determine the z-value of the height if a student chosen at random has a height of less than 162 cm. (b) Hence, the probability of chosen a student of such height.
3. The score of a class for a monthly test are normally distributed with a mean of 48 marks and a standard deviation of 15 marks. Determine the z-value for the marks between 40 marks and 65 marks. Hence, the probability of chosen a student with such the range of scores.
4. The scores of Add. Maths test for a class are normally distributed with a mean of 55 marks and a standard deviation of 16. Determine (a) the z-value of the scores if a student is chosen with the marks less than 40. (b) the probability of chosen such a student.
5. The volume of bottled fruit juice produced by a factory are normally distributed with a mean of 750 ml and a standard deviation of 12 ml. If a bottle of the fruit juice is chosen at random, find, (a) the z-value of the volume of the fruit is less than 740 ml, (b) the probability of chosen such the volume of the fruit juice.
6. X is a random variable of a normal distribution with a mean of 34 and a variance of 9. Find (a) the z-value for X is between 34 and 37. (b) the probability for 31<X<37.
edmet-nklpunya.blogspot.com
11
20.3 PAST YEAR QUESTIONS Exercise 20.3.1 SPM Paper 1 SPM 2005: The mass of students in a school has a normal distribution with a mean of 54 kg and a standard deviation of 12 kg. Find (a) the mass of the students which gives a standard score of 0.5, (b) the percentage of students with mass greater than 48 kg. [4 marks] SPM 2007: X is continuous random variable of a normal distribution with a mean of 52 and a standard deviation of 10. Find (a) the z-score when X = 67.2 (b) the value of k when P(z < k) = 0.8849 [ 4 marks]
SPM 2006: Diagram 10 shows a standard normal distribution graph. The probability represented f(z) by the area of the shaded region is 0.3485. 0.3485 (a) Find the value of k.
0 k z
SPM 2007 The probability that each shot fired by Ramli hits a target is 1 .
3
(a) If Ramli fires 10 shots, find the probability that exactly 2 shaots hit the target. (b) If Ramli fires n shots, the probability that all the n shots hit the target is Find the value of n.
1 . 243
(b) X is a continuous random variable is normally Diagram 10 distributed with a mean of 79 and a standard deviation of 3. Find the value of X when the z-score is k [4 marks]
[4 marks]
edmet-nklpunya.blogspot.com
12
SPM2008: The masses of students in a school have a normal distribution with a mean of 40 kg and a standard deviation of 5 kg. Calculate the probability that a student chosen at random from this group has a mass of (a) more than 45 kg, (b) between 35 kg and 47.8 kg. [4 marks]
SPM 2009: The masses of apples in a stall have a normal distribution with a mean of 200 g and a standard deviation of 30 g. (a) Find the mass, in g, of an apple whose z-score is 0.5. (b) If an apple is chosen at random, find the probability that the apple has a mass of at least 194 g. [ 4 marks]
SPM 2010: The discrete random variable X has a binomial probability distribution with n = 4, where n is the number of trials. Diagram 25 shows the probability distribution of X. P( X = x) k
1 4
SPM 2004: X is a random variable of a normal distribution with a mean of 5.2 and a variance of 1.44. Find (a) the z value if X = 6.7 (b) P(5.2 X 6.7). [4 marks]
Diagram 25
1 16
x
0 1 2 3 4
Find (a) the value of k. (b) P(X 3).
[4 marks]
edmet-nklpunya.blogspot.com
13
Exercise 20.3.2 SPM Paper 2 SPM 2005: (a)The result of a study shows that 20% of the pupils in a city cycle to school. If 8 pupils from the city are chosen at random, calculate the probability that (a) exactly 2 of them cycle to school. (b) less than 3 of them cycle to school. [4 marks]
(b) The masses of water melons produced from an orchard follow a normal distribution with a mean of 3.2 kg and a standard deviation of 0.5 kg. Find (i) the probability that the watermelon chosen randomly from the orchard has a mass of not more than 40 kg. (ii) the value of m if 60 % of the watermelons from the orchard have a mass of more than m kg. [6 marks]
edmet-nklpunya.blogspot.com
14
SPM 2006: An orchard produces lemon. Only lemons with diameter , x greater than k cm are graded and marketed. Table 3 shows the grades of the lemons based on their diameters. Grade Diameter, x (cm) A x>7 B 7x>5 C 5 x > k
Table 3
It is given that diameters of the lemons have a normal distribution with a mean of 5.8 cm and a standard deviation of 1.5 cm. (a) (b) (c) If one lemon is picked at random, calculate the probability that it is of grade A. In a basket of 500 lemons, estimate the number of grade B lemons. If 85.7% of the lemons is marketed, find the value of k. [2 marks] [2 marks] [4 marks]
edmet-nklpunya.blogspot.com
15
SPM 2007: (a) In a survey carried out in a school, it is found that 2 out 5 students have handphones. If 8 students from that school are chosen at random, calculate the probability that (i) exactly 2 students have handphones, i. (ii) more than 2 students have handphones. [5 marks]
(b) A group of workers are given medical check up. The blood pressure of a worker has a normal distribution with a man of 130 mmHg and a standard deviation of 16 mmHg. Blood pressure that is more than 150 mmHg is classified as high blood pressure. (i) A worker is chosen at random from the group. Find the probability that the worker has a blood pressure between 114 mmHg and 150 mmHg.more than 40 kg. (ii) It is found that 132 workers have high blood pressure. Find the total number of workers in the group. [5 marks]
edmet-nklpunya.blogspot.com
16
SPM 2008: The masses of mangoes from an orchard have a normal distribution with a mean of 300 g and a standard deviation 0f 80 g. (a) Find the probability that a mango chosen randomly from this orchard has a mass of more than 168 g. [3 marks]
(b) A random sample of 500 mangoes is chosen. (i) Calculate the number of mangoes from this sample that have a mass of more than 168 g. (ii) Given that 435 mangoes from this sample have a mass of more than m g, find the value of m. [7 marks]
edmet-nklpunya.blogspot.com
17
SPM 2009: A test paper consists of 40 questions. Each question is followed by four choices of answer, where only one of these is correct. (a) i. Salma answers all the questions by randomly choosing an answer for each question. (i) Estimate the number of questions she answered correctly. (ii) Find the standard deviation of the number of questions she answered correctly. [5 marks]
(b)
Basri answers 30 questions correctly and randomly chooses an answer for each of the remaining 10 questions. Find the probability that he answers. (i) 36 questions correctly, (ii) at least 32 questions correctly. [5 marks]
edmet-nklpunya.blogspot.com
18
SPM 2010: (a) A random variable, X, has a binomial distribution with 10 trials where the probability of success in each trial is p. The mean number of success is 4. calculate (i) the value of p, ii. (ii) P(X 2) [5 marks]
(b) The diameters of limes from a farm have a normal distribution with a mean of 3.2 cm and a standard deviation of 1.5 cm. Calculate (i) the probability that a lime chosen at random from this farm has a diameter of more than 3.9 cm. (ii) the value of d if 33% of the limes have diameters less than d cm. [5 marks]
edmet-nklpunya.blogspot.com
19
SPM 2004: (a) A club organizes a practice session for trainees on scoring goals from penalty kicks. Each trainee takes 8 penalty kicks. The probability that a trainee scores a goal from a penalty kick is p. After the session, it is found that the mean number of goals for a trainee is 4.8. (i) Find the value of p. iii. (ii) If a trainee is chosenat random, find the probability that he scores at least one goal. [5 marks]
(b) A survey on body-mass is done on a group of students. The mass of a student has a normal distribution with a mean of 50 kg and a standard deviation of 15 kg. (i) If a student is chosen at random, calculate the probability that his mass is less than 41 kg. (ii) Given that 12% of the students have a mass of more than m kg, find the value of m. [5 marks]
edmet-nklpunya.blogspot.com
20
SPM 2003: (a) Senior citizens make up 20% of the population of a settlement. (i) iv. If 7 people are randomly selected from the settlement, find the probability that at least two of them are senior citizens. [5 marks]
(ii) If the variance of the senior citizens is 128, what is the populations of the settlement?
(b) The mass of the workers in a factory is normally distributed with a mean of 67.86 kg and a variance of 42.25 kg2. 200 of the workers in the factory weigh between 50 kg and 70 kg. Find the total number of workers in the factory. [5 marks]
edmet-nklpunya.blogspot.com
21
THE END
You might also like
- Bengkel Add Maths - Taburan KebarangkalianDocument13 pagesBengkel Add Maths - Taburan KebarangkalianAbdul Manaf0% (1)
- Math PT3 Revision 1 2 3Document5 pagesMath PT3 Revision 1 2 3Noor Fazliati SulaimanNo ratings yet
- Linear ProgrammingDocument13 pagesLinear ProgrammingSuziana MohamadNo ratings yet
- Math SPM Trial 2013 Kedah p1 AnsDocument34 pagesMath SPM Trial 2013 Kedah p1 AnschuaNo ratings yet
- Chapter 2: Number Pattern & Sequence (Notes & Exercise)Document7 pagesChapter 2: Number Pattern & Sequence (Notes & Exercise)Gurpreet100% (1)
- Simultaneous Linear Equation f1 ExerciseDocument4 pagesSimultaneous Linear Equation f1 ExerciseJenny GohNo ratings yet
- Modul 3 Rumus Algebra k1Document3 pagesModul 3 Rumus Algebra k1Mohd FareedNo ratings yet
- Bank Soalan Trigonometry Paper2Document10 pagesBank Soalan Trigonometry Paper2pizamNo ratings yet
- Linear Programming SPM 2003 - 2007Document2 pagesLinear Programming SPM 2003 - 2007Rosmizar AhmadNo ratings yet
- Soalan Set 1Document16 pagesSoalan Set 1Pauling ChiaNo ratings yet
- Jom Tanya Sifu :15 Days Programme Part 1Document15 pagesJom Tanya Sifu :15 Days Programme Part 1Hayati Aini AhmadNo ratings yet
- SYLLABUS PT3 MathDocument3 pagesSYLLABUS PT3 MathApek TebuNo ratings yet
- Chapter 12 II Transformations III SPM Past Year Questions 2Document8 pagesChapter 12 II Transformations III SPM Past Year Questions 2Samsiah Mustaffa100% (1)
- Soalan BulatanDocument5 pagesSoalan BulatanSahafuddin Ahmad FadzilNo ratings yet
- Soalan Set 1Document13 pagesSoalan Set 1Pauling ChiaNo ratings yet
- SPM Science Soalan RamalanDocument15 pagesSPM Science Soalan RamalanLow Fang Khim100% (1)
- Chapter 11: Index NumberDocument7 pagesChapter 11: Index NumberHayati Aini AhmadNo ratings yet
- Addmath Form 4Document11 pagesAddmath Form 4fariha ayuniNo ratings yet
- Latihan - Penaakulan Logik 1Document11 pagesLatihan - Penaakulan Logik 1meghan0% (1)
- Chapter 9: DifferentiationDocument10 pagesChapter 9: DifferentiationHayati Aini AhmadNo ratings yet
- Add Maths Form 4 Paper 1 Midterm 2012Document18 pagesAdd Maths Form 4 Paper 1 Midterm 2012Thiyaku MaruthaNo ratings yet
- Skema Biologi k3 SPM 2010Document11 pagesSkema Biologi k3 SPM 2010fatimahmni100% (1)
- PHY07Document190 pagesPHY07sazliman100% (2)
- Vector SPM 2003 - 2007Document4 pagesVector SPM 2003 - 2007Rosmizar AhmadNo ratings yet
- SPM Sains ModulDocument16 pagesSPM Sains ModulAzlin MohdNo ratings yet
- 2 Klon SPM Quad Eqn 2003 - 2014 - EdDocument32 pages2 Klon SPM Quad Eqn 2003 - 2014 - EdAnonymous 0fagPbbloNo ratings yet
- PBS Maths F1 Chapter 9Document10 pagesPBS Maths F1 Chapter 9Ai LanNo ratings yet
- Modul Cemerlang Matematik JPN Kedah 2016 PDFDocument102 pagesModul Cemerlang Matematik JPN Kedah 2016 PDFAnna ZubirNo ratings yet
- SPM Questions (Differentiation) - Paper 2Document4 pagesSPM Questions (Differentiation) - Paper 2Sanjey RamakrishnanNo ratings yet
- Mathematics KSSM Form 3: Chapter 9:straight LinesDocument13 pagesMathematics KSSM Form 3: Chapter 9:straight LinesNUR RAIHAN BINTI ABDUL RAHIM MoeNo ratings yet
- Sijil Pelajaran Malaysia Mulai Tahun 2021: Senarai RumusDocument4 pagesSijil Pelajaran Malaysia Mulai Tahun 2021: Senarai RumusLh MooNo ratings yet
- AMATH Simultaneous EquationDocument7 pagesAMATH Simultaneous EquationLeneNo ratings yet
- Rumus Fizik 2021Document1 pageRumus Fizik 2021Azizi Abdullah100% (1)
- MATHEMATICS Form 1 PercentagesDocument18 pagesMATHEMATICS Form 1 PercentagesG Nathan JdNo ratings yet
- Bengkel Skema Pemarkahan Fizik Kertas'3Document39 pagesBengkel Skema Pemarkahan Fizik Kertas'3Salmizam IzamNo ratings yet
- Addmath Exercise Form 4Document2 pagesAddmath Exercise Form 4Ainun SyakirahNo ratings yet
- 6 Coordinate GeometryDocument17 pages6 Coordinate GeometryMJ ChowNo ratings yet
- Kertas 2 SPM Matematik Tambahan 2004-2010Document49 pagesKertas 2 SPM Matematik Tambahan 2004-2010Cikgu Mohamad Esmandi HapniNo ratings yet
- Loci in Two DimensionDocument7 pagesLoci in Two DimensionSathis KumarNo ratings yet
- SPM Questions (Differentiation)Document2 pagesSPM Questions (Differentiation)Balkis Abdul ManafNo ratings yet
- Modul Matematik Tambahan Form 5 (JPNP)Document110 pagesModul Matematik Tambahan Form 5 (JPNP)Fazlina Mustafa0% (1)
- SPM Form 4 Add Math Revision Note - Differentiation 3Document6 pagesSPM Form 4 Add Math Revision Note - Differentiation 3MyHomeTuition.com50% (4)
- IT Phy F5 Topical Test 2 (BL)Document12 pagesIT Phy F5 Topical Test 2 (BL)Jeemion JealiNo ratings yet
- Matematik K1 Trial SPM SBP 2019Document28 pagesMatematik K1 Trial SPM SBP 2019Fendi A. Bakar75% (4)
- Modul Cemerlang Matematik JPN Kedah 2016 (Jawapan) PDFDocument43 pagesModul Cemerlang Matematik JPN Kedah 2016 (Jawapan) PDFAnna Zubir100% (1)
- MODULE 16 PMR - Scale Drawing Solid GeometryDocument6 pagesMODULE 16 PMR - Scale Drawing Solid GeometryDerek MaNo ratings yet
- Koleksi Soalan Matematik Tambahan SPM 2004-2009-DifferentiationDocument10 pagesKoleksi Soalan Matematik Tambahan SPM 2004-2009-DifferentiationSforazzura Suhaimi50% (6)
- Form 3 Mathematics Chapter 1 (Indices) KSSMDocument2 pagesForm 3 Mathematics Chapter 1 (Indices) KSSMBONG TZER WEI MoeNo ratings yet
- Soalan Kbat Add Math Form 5Document8 pagesSoalan Kbat Add Math Form 5Eric Mooi50% (2)
- Vector Paper 2 PDFDocument12 pagesVector Paper 2 PDFՙՙՙՙNo ratings yet
- CHP 8.2 Normal (Mon) W26Document8 pagesCHP 8.2 Normal (Mon) W26Bid HassanNo ratings yet
- Probability Distribution (2010)Document7 pagesProbability Distribution (2010)Amir ZulkifliNo ratings yet
- Add Math C5 Ex - TeachDocument21 pagesAdd Math C5 Ex - Teach凯帆杨No ratings yet
- Probability DistributionsDocument14 pagesProbability DistributionsNurul Hidayah MuhammadNo ratings yet
- Review Final2021Document18 pagesReview Final2021sports8854346No ratings yet
- Binomial Distribution (Taburan Binomial) : Example 1Document14 pagesBinomial Distribution (Taburan Binomial) : Example 1Abdul ManafNo ratings yet
- StatsB TheBinomialDistributionDocument4 pagesStatsB TheBinomialDistributionShane LambertNo ratings yet
- 19ProbablityDistributionsF5 BinomialDocument6 pages19ProbablityDistributionsF5 BinomialFazlina MustafaNo ratings yet
- Module 18 Probability DistributionsDocument34 pagesModule 18 Probability DistributionstheuniquecollectionNo ratings yet
- SAT Math Level 2 Subject Test Practice Problems 2013 EditionFrom EverandSAT Math Level 2 Subject Test Practice Problems 2013 EditionRating: 1 out of 5 stars1/5 (1)
- 0606 VectorDocument11 pages0606 VectorTee Pei LengNo ratings yet
- Band 6 Science Form 1Document49 pagesBand 6 Science Form 1Tee Pei Leng0% (1)
- Vectors PPQs PDFDocument4 pagesVectors PPQs PDFTee Pei LengNo ratings yet
- Linear Law TrialDocument6 pagesLinear Law TrialTee Pei LengNo ratings yet
- Trial SPM Paper 2 Questions-LINEAR LAW: X B A y yDocument4 pagesTrial SPM Paper 2 Questions-LINEAR LAW: X B A y yTee Pei LengNo ratings yet
- C 11 3 DimensionDocument6 pagesC 11 3 DimensionTee Pei LengNo ratings yet
- F4C1 FunctionsDocument12 pagesF4C1 FunctionsTee Pei LengNo ratings yet
- Coordinate Geometry Ver 2012Document19 pagesCoordinate Geometry Ver 2012Tee Pei LengNo ratings yet
- Additional Mathematics: Form 5Document19 pagesAdditional Mathematics: Form 5Tee Pei LengNo ratings yet
- Bab 10 - Pengaturcaraan Linear: y X X y X y X y X y XDocument3 pagesBab 10 - Pengaturcaraan Linear: y X X y X y X y X y XTee Pei LengNo ratings yet
- Earthquake Project On LogarithmsDocument7 pagesEarthquake Project On LogarithmsTee Pei LengNo ratings yet
- Chapter 8 - Solid Geometry 3Document2 pagesChapter 8 - Solid Geometry 3Tee Pei LengNo ratings yet
- SPM Question Form 4 Solution of TrianglesDocument6 pagesSPM Question Form 4 Solution of TrianglesTee Pei LengNo ratings yet
- Probability Edit 2012Document8 pagesProbability Edit 2012Tee Pei LengNo ratings yet
- Lesson 86 Activity Sheet 1Document1 pageLesson 86 Activity Sheet 1Tee Pei LengNo ratings yet
- Nota Ekpress PMR SainsDocument12 pagesNota Ekpress PMR SainsTee Pei LengNo ratings yet
- Lesson 106 Activity Sheet 1Document5 pagesLesson 106 Activity Sheet 1Tee Pei LengNo ratings yet
- Chapter 6:coordinate Geometry: X X y yDocument20 pagesChapter 6:coordinate Geometry: X X y yTee Pei LengNo ratings yet
- Mathematics For UsersDocument222 pagesMathematics For UsersbongoherbertNo ratings yet
- ALEVEL Math Pepr 2 Set 2Document5 pagesALEVEL Math Pepr 2 Set 2mwesigwaaNo ratings yet
- Probability Question BankDocument49 pagesProbability Question Banksebastianikeda25No ratings yet
- Business Statistics For Contemporary Decision Making 8th Edition Black Solutions Manual 1Document31 pagesBusiness Statistics For Contemporary Decision Making 8th Edition Black Solutions Manual 1helen100% (33)
- Mahler Practice Exam 1Document19 pagesMahler Practice Exam 1Chong Yin WaiNo ratings yet
- FullDocument1,224 pagesFullfbn2377No ratings yet
- X X N X 63+74+42+65+51+54+36+56+68+57+ X 2,616 X 65.4Document11 pagesX X N X 63+74+42+65+51+54+36+56+68+57+ X 2,616 X 65.4Play Ind1eNo ratings yet
- Chapter 8: Probability Distributions 1. Understand and Use The Concept of Binomial DistributionDocument14 pagesChapter 8: Probability Distributions 1. Understand and Use The Concept of Binomial DistributionrahimNo ratings yet
- Image Denoising Using Wavelet Thresholding and Model SelectionDocument4 pagesImage Denoising Using Wavelet Thresholding and Model SelectionjebileeNo ratings yet
- Random Variable Using MATLABDocument14 pagesRandom Variable Using MATLABomars_engNo ratings yet
- Robind@nitrkl - Ac.in Sarkarp@nitrkl - Ac.in Sujithmss@gatech - EduDocument24 pagesRobind@nitrkl - Ac.in Sarkarp@nitrkl - Ac.in Sujithmss@gatech - EduShemin T JohnNo ratings yet
- Statistical Learning: Problem Set 1: Problem 1 - Frequentist Decision TheoryDocument4 pagesStatistical Learning: Problem Set 1: Problem 1 - Frequentist Decision TheorySalman AlghifaryNo ratings yet
- Catena: Isabel Campos, Carlos Vale, Nelson Abrantes, Jan Jacob Keizer, Patrícia PereiraDocument11 pagesCatena: Isabel Campos, Carlos Vale, Nelson Abrantes, Jan Jacob Keizer, Patrícia Pereiramelimeli106No ratings yet
- (Q R) Inventory Model With Variable Lead Time When The Amount Received Is UncertainDocument14 pages(Q R) Inventory Model With Variable Lead Time When The Amount Received Is UncertainInfuzziana Arlin HatzNo ratings yet
- Week4 - Probability and Cenral TendencyDocument59 pagesWeek4 - Probability and Cenral TendencybioiboNo ratings yet
- Excel Plot Normal PDFDocument2 pagesExcel Plot Normal PDFJacquelineNo ratings yet
- Kemiringan Dan Penggunaan Standar DeviasiDocument4 pagesKemiringan Dan Penggunaan Standar DeviasiProdi Arsitektur UntanNo ratings yet
- Unit 4 - Continuous Random VariablesDocument35 pagesUnit 4 - Continuous Random VariablesShouq AbdullahNo ratings yet
- The Poisson Distribution: Are Both Equal To The Parameter LDocument19 pagesThe Poisson Distribution: Are Both Equal To The Parameter LCharmianNo ratings yet
- Midterm ExamDocument32 pagesMidterm Examriza cabugnaoNo ratings yet
- Bayesian Online Changepoint DetectionDocument7 pagesBayesian Online Changepoint DetectionChikh YassineNo ratings yet
- R18 B.tech Ii YearDocument29 pagesR18 B.tech Ii YearK SrinuNo ratings yet
- Estimation and Detection: Lecture 9: Introduction Detection Theory (Chs 1,2,3)Document38 pagesEstimation and Detection: Lecture 9: Introduction Detection Theory (Chs 1,2,3)akhilarajNo ratings yet
- Week 2 Measures of Dispersion IIDocument34 pagesWeek 2 Measures of Dispersion IITildaNo ratings yet
- Chap5 Statistical InferenceDocument37 pagesChap5 Statistical InferenceNIHIR AgarwalNo ratings yet
- On The Choice of A Demand Distribution For Inventory Management ModelsDocument15 pagesOn The Choice of A Demand Distribution For Inventory Management ModelsSimran MittalNo ratings yet
- Business Stat CH 1Document15 pagesBusiness Stat CH 1Natnael AsfawNo ratings yet
- Iso-Tc69 N 778 (2007)Document25 pagesIso-Tc69 N 778 (2007)Boris Chicoma0% (1)
- Activity 5 StatDocument6 pagesActivity 5 StatGene Roy P. HernandezNo ratings yet
- HW 7Document4 pagesHW 7adithya604No ratings yet