Professional Documents
Culture Documents
Chapter 4 Applications of Derivatives: 4.1 Extreme Values of Functions
Uploaded by
Umut özdemirOriginal Description:
Original Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
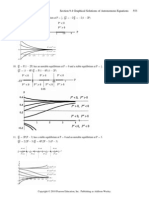
Report this DocumentCopyright:
Available Formats
Chapter 4 Applications of Derivatives: 4.1 Extreme Values of Functions
Uploaded by
Umut özdemirCopyright:
Available Formats
CHAPTER 4 APPLICATIONS OF DERIVATIVES
4.1 EXTREME VALUES OF FUNCTIONS
1. An absolute minimum at x c# , an absolute maximum at x b. Theorem 1 guarantees the existence of such
extreme values because h is continuous on [a b].
2. An absolute minimum at x b, an absolute maximum at x c. Theorem 1 guarantees the existence of such
extreme values because f is continuous on [a b].
3. No absolute minimum. An absolute maximum at x c. Since the function's domain is an open interval, the
function does not satisfy the hypotheses of Theorem 1 and need not have absolute extreme values.
4. No absolute extrema. The function is neither continuous nor defined on a closed interval, so it need not fulfill
the conclusions of Theorem 1.
5. An absolute minimum at x a and an absolute maximum at x c. Note that y g(x) is not continuous but
still has extrema. When the hypothesis of Theorem 1 is satisfied then extrema are guaranteed, but when the
hypothesis is not satisfied, absolute extrema may or may not occur.
6. Absolute minimum at x c and an absolute maximum at x a. Note that y g(x) is not continuous but still
has absolute extrema. When the hypothesis of Theorem 1 is satisfied then extrema are guaranteed, but when
the hypothesis is not satisfied, absolute extrema may or may not occur.
7. Local minimum at ac" !b, local maximum at a" !b
8. Minima at ac# !b and a# !b, maximum at a! #b
9. Maximum at a! &b. Note that there is no minimum since the endpoint a# !b is excluded from the graph.
10. Local maximum at ac$ !b, local minimum at a# !b, maximum at a" #b, minimum at a! c"b
11. Graph (c), since this the only graph that has positive slope at c.
12. Graph (b), since this is the only graph that represents a differentiable function at a and b and has negative slope at c.
13. Graph (d), since this is the only graph representing a funtion that is differentiable at b but not at a.
14. Graph (a), since this is the only graph that represents a function that is not differentiable at a or b.
15. f has an absolute min at x 0 but does not have an absolute
max. Since the interval on which f is defined, c1 x 2,
is an open interval, we do not meet the conditions of
Theorem 1.
Copyright 2010 Pearson Education, Inc. Publishing as Addison-Wesley.
168
Chapter 4 Applications of Derivatives
16. f has an absolute max at x 0 but does not have an absolute
min. Since the interval on which f is defined, c1 x 1, is
an open interval, we do not meet the conditions of
Theorem 1.
17. f has an absolute max at x 2 but does not have an absolute
min. Since the function is not continuous at x 1, we do
not meet the conditions of Theorem 1.
18. f has an absolute max at x 4 but does not have an absolute
min. Since the function is not continuous at x 0, we do
not meet the conditions of Theorem 1.
19. f has an absolute max at x
x
31
2 .
1
2
and an absolute min at
Since the interval on which f is defined,
0 x 21, is an open interval, we do not meet the
conditions of Theorem 1.
20. f has an absolute max at x 0 and an absolute min at
x 1 and x c1. Since f is continuous on the closed
2
interval on which it is defined, c1 x 21, we do meet
the conditions of Theorem 1.
21. f(x)
2
3
x c 5 f w (x)
f(c2) c
19
3 ,
2
3
no critical points;
f(3) c3 the absolute maximum
is c3 at x 3 and the absolute minimum is c 19 at
3
x c2
Copyright 2010 Pearson Education, Inc. Publishing as Addison-Wesley.
Section 4.1 Extreme Values of Functions
22. f(x) cx c 4 f w (x) c1 no critical points;
f(c4) 0, f(1) c5 the absolute maximum is 0
at x c4 and the absolute minimum is c5 at x "
23. f(x) x# c 1 f w (x) 2x a critical point at
x 0; f(c1) 0, f(0) c1, f(2) 3 the absolute
maximum is 3 at x 2 and the absolute minimum is c1
at x 0
24. f(x) % c x# f w (x) c2x a critical point at
x 0; f(c3) c5, f(0) 4, f(1) 3 the absolute
maximum is 4 at x 0 and the absolute minimum is c5
at x c3
2
x
"
25. F(x) c x cxc# Fw (x) 2xc$
, however
x 0 is not a critical point since 0 is not in the domain;
F(0.5) c4, F(2) c0.25 the absolute maximum is
c0.25 at x 2 and the absolute minimum is c4 at
x 0.5
"
x
26. F(x) c " cxc" Fw (x) xc#
x
, however
x 0 is not a critical point since 0 is not in the domain;
F(c2) " , F(c1) 1 the absolute maximum is 1 at
#
x c1 and the absolute minimum is
27. h(x) $ x x"$ hw (x)
"
3
"
#
at x c2
xc#$ a critical point
at x 0; h(c1) c1, h(0) 0, h(8) 2 the absolute
maximum is 2 at x 8 and the absolute minimum is c1
at x c1
Copyright 2010 Pearson Education, Inc. Publishing as Addison-Wesley.
169
170
Chapter 4 Applications of Derivatives
28. h(x) c3x#$ hw (x) c#xc"$ a critical point at
x 0; h(c1) c3, h(0) 0, h(1) c3 the absolute
maximum is 0 at x 0 and the absolute minimum is c3
at x 1 and at x c1
gw (x)
"
#
a4 c x# b
c"#
"#
(c2x)
cx
4 c x
29. g(x) 4 c x# a4 c x# b
critical points at x c2 and x 0, but not at x 2
because 2 is not in the domain; g(c2) 0, g(0) 2,
g(1) 3 the absolute maximum is 2 at x 0 and the
absolute minimum is 0 at x c2
30. g(x) c5 c x# c a& c x# b
a5 c x# b
(c2x)
x
"
w
g (x) c #
critical points at x c5
"#
&cx
c"#
and x 0, but not at x 5 because 5 is not in the
domain; f c5 0, f(0) c5
the absolute maximum is 0 at x c5 and the absolute
minimum is c5 at x 0
31. f()) sin ) f w ()) cos ) )
1
#
is a critical point,
is not a critical point because c1 is not interior to
#
1
the domain; f c1 c1, f 1 1, f 56 "
#
#
#
but )
c1
#
the absolute maximum is 1 at )
minimum is c1 at )
c1
#
1
#
and the absolute
32. f()) tan ) f w ()) sec# ) f has no critical points in
c1 1 . The extreme values therefore occur at the
3 4
endpoints: f c1 c3 and f 1 1 the absolute
3
4
maximum is 1 at ) 1 and the absolute
4
minimum is c3 at ) c1
3
Copyright 2010 Pearson Education, Inc. Publishing as Addison-Wesley.
Section 4.1 Extreme Values of Functions
171
33. g(x) csc x gw (x) c(csc x)(cot x) a critical point
1
2
2
at x 1 ; g 1 3 , g 1 1, g 23 3 the
#
#
3
absolute maximum is
at x
2
3
absolute minimum is 1 at x
1
3
and x
21
3 ,
and the
1
#
34. g(x) sec x gw (x) (sec x)(tan x) a critical point at
2
x 0; g c 1 2, g(0) 1, g 1 3 the absolute
3
6
maximum is 2 at x c 1 and the absolute minimum is 1
3
at x 0
35. f(t) 2 c ktk # c t# # c at# b
c"#
t
(2t) c c kttk
t
f w (t) c " at# b
#
"#
a critical point at t 0; f(c1) 1,
f(0) 2, f(3) c1 the absolute maximum is 2 at t 0
and the absolute minimum is c1 at t 3
36. f(t) kt c 5k (t c 5)# a(t c 5)# b
"
#
a(t c 5)# b
c"#
(2(t c 5))
tc5
(t c 5)
"#
f w (t)
tc5
kt c 5 k
a critical point at t 5; f(4) 1, f(5) 0, f(7) 2
the absolute maximum is 2 at t 7 and the absolute
minimum is 0 at t 5
37. f(x) x%$ f w (x)
4
3
x"$ a critical point at x 0; f(c1) 1, f(0) 0, f(8) 16 the absolute
maximum is 16 at x 8 and the absolute minimum is 0 at x 0
38. f(x) x&$ f w (x)
5
3
x#$ a critical point at x 0; f(c1) c1, f(0) 0, f(8) 32 the absolute
maximum is 32 at x 8 and the absolute minimum is c1 at x c1
39. g()) )$& gw ())
3
5
)c#& a critical point at ) 0; g(c32) c8, g(0) 0, g(1) 1 the absolute
maximum is 1 at ) 1 and the absolute minimum is c8 at ) c32
40. h()) 3)#$ hw ()) 2)c"$ a critical point at ) 0; h(c27) 27, h(0) 0, h(8) 12 the absolute
maximum is 27 at ) c27 and the absolute minimum is 0 at ) 0
41. y x2 c 6x b 7 y w 2x c 6 2x c 6 0 x 3. The critical point is x 3.
42. faxb 6x2 c x3 f w axb 12x c 3x2 12x c 3x2 0 3xa4 c xb 0 x 0 or x 4. The critical pointss are
x 0 and x 4.
Copyright 2010 Pearson Education, Inc. Publishing as Addison-Wesley.
172
Chapter 4 Applications of Derivatives
43. faxb xa4 c xb3 f w axb x<3a4 c xb2 ac1b b a4 c xb3 a4 c xb2 <c3x b a4 c xb a4 c xb2 a4 c 4xb
4a4 c xb2 a1 c xb 4a4 c xb2 a1 c xb 0 x 1 or x 4. The critical points are x 1 and x 4.
44. gaxb ax c 1b2 ax c 3b2 g w axb ax c 1b2 2ax c 3ba1b b 2ax c 1ba1b ax c 3b2
2ax c 3bax c 1b<ax c 1b b ax c 3b 4ax c 3bax c 1bax c 2b 4ax c 3bax c 1bax c 2b 0 x 3 or x 1 or
x 2. The critical points are x 1, x 2, and x 3.
45. y x2 b
2
x
y w 2x c
2
x2
2x3 c 2
x2
2x3 c 2
x2
! 2x3 c 2 ! x 1;
2x3 c 2
x2
undefined x2 0 x 0.
The domain of the function is ac_, 0b r a0, _b, thus x 0 is not in the domain, so the only critical point is x 1.
46. faxb
f w axb
x2
xc2
ax c 2b2x c x2 a1b
ax c 2 b 2
x2 c 4x
ax c 2 b 2
x2 c 4x
ax c 2 b 2
! x2 c 4x ! x 0 or x 4;
x2 c 4x
ax c 2 b 2
undefined
ax c 2b 0 x 2. The domain of the function is ac_, 2b r a2, _b, thus x 2 is not in the domain, so the only
critical points are x 0 and x 4
2x3 2 c 16
x
2x3 2 c 16
x
16
x
! 2x32 c 16 0 x 4;
2x3 2 c 16
x
47. y x2 c 32x y w 2x c
undefined
x 0 x 0. The critical points are x 4 and x 0.
48. gaxb 2x c x2 g w axb
1cx
2x c x2
1cx
2x c x2
0 1 c x 0 x 1;
1cx
2x c x2
undefined 2x c x2 0
2x c x2 0 x 0 or x 2. The critical points are x 0, x 1, and x 2.
49. Minimum value is 1 at x 2.
50. To find the exact values, note that yw 3x2 c 2,
which is zero when x 2 . Local maximum at
3
c 2 4 b
3
4 6
9
ac0816 5089b; local
minimum at # % c
$
% '
*
a0.816 2.911b
Copyright 2010 Pearson Education, Inc. Publishing as Addison-Wesley.
Section 4.1 Extreme Values of Functions
51. To find the exact values, note that that yw 3x2 b 2x c 8
a3x c 4bax b 2b, which is zero when x c2 or x % .
$
Local maximum at ac2 17b; local minimum at % c %"
$
#(
52. Note that yw 5x# ax c 5bax c 3b, which is zero at
x 0, x 3, and x 5. Local maximum at a3, 108b;
local minimum at a5, 0b; a0, 0b is neither a maximum nor
a minimum.
53. Minimum value is 0 when x c" or x ".
54. Note that yw
x c 2
x ,
which is zero at x 4 and is
undefined when x 0. Local maximum at a0, 0b;
absolute minimum at a4, c4b
55. The actual graph of the function has asymptotes at x ",
so there are no extrema near these values. (This is an
example of grapher failure.) There is a local minimum at
a! "b.
Copyright 2010 Pearson Education, Inc. Publishing as Addison-Wesley.
173
174
Chapter 4 Applications of Derivatives
56. Maximum value is 2 at x ";
minimum value is 0 at x c" and x $.
"
# at x "
c " as x c".
#
57. Maximum value is
minimum value is
"
# at x 0
c " as x c2.
#
58. Maximum value is
59. yw x#$ a"b b # xc"$ ax b #b
$
crit. pt.
x c%
&
x!
derivative
!
undefined
&x b %
$ x
extremum
local max
local min
minimum value is
value
"#
"$
"!$%
#& "!
0
Copyright 2010 Pearson Education, Inc. Publishing as Addison-Wesley.
Section 4.1 Extreme Values of Functions
derivative
!
undefined
!
a"b% c x#
crit. pt.
x c#
x c #
x #
x#
value
c$
0
$
extremum
minimum
local max
minimum
"
a c #xb b
# % c x
cx b a% c x b
%
c #x
% c x
%cx
61. yw x
crit. pt.
x c"
x!
x"
)x c )
$ x
$
60. yw x#$ a#xb b # xc"$ ax# c %b
$
derivative
undefined
!
!
undefined
extremum
local max
minimum
maximum
local min
value
!
c#
#
!
"
62. yw x# #$ c x a c 1b b #x$ c x
cx b a%xba$ c xb
# $ c x
#
crit. pt.
x0
x "#
&
x$
_5x b "#x
# $ c x
#
derivative
!
!
undefined
extremum
minimum
local max
minimum
value
!
"%%
"#
%%'#
"#& "&
!
extremum
minimum
value
#
c#, x "
63. yw
", x "
crit. pt.
x"
64. yw
crit. pt.
x!
x"
derivative
undefined
c",
# c #x,
x!
x!
derivative
undefined
!
extremum
local min
local max
value
$
%
Copyright 2010 Pearson Education, Inc. Publishing as Addison-Wesley.
175
176
Chapter 4 Applications of Derivatives
c2x c 2,
65. yw
c2x b 6,
crit. pt.
x c1
x1
x3
x1
x1
derivative
!
undefined
!
extremum
maximum
local min
maximum
value
5
1
5
c " x# c " x b "& , x "
%
#
%
x$ c 'x# b )x,
x"
w
w
#
if x ", and lim f a" b hb c". Also, f axb $x c "#x b ) if x ", and
66. We begin by determining whether f w axb is defined at x ", where faxb
"
#
h!
Clearly, f w axb c " x c
#
lim f w a" b hb c". Since f is continuous at x ", we have that f w a"b c". Thus,
f w axb
c"x c ",
#
#
$x c "#x b ) ,
#
Note that c " x c
#
But # c
# $
$
crit. pt.
x c"
x $"&&
"
#
x"
x"
! when x c", and $x# c "#x b ) ! when x
!)%& ", so the critical points occur at x c" and x
derivative
!
!
extremum
local max
local min
"# "# c %a$ba)b
"# ' %)
#a$b
# b # $ $ $"&&.
#
h!
#$
$ .
value
4
c$!(*
67. (a) No, since f w axb # ax c #bc"$ , which is undefined at x #.
$
(b) The derivative is defined and nonzero for all x #. Also, fa#b ! and faxb ! for all x #.
(c) No, faxb need not have a global maximum because its domain is all real numbers. Any restriction of f to a closed
interval of the form a, b would have both a maximum value and minimum value on the interval.
(d) The answers are the same as (a) and (b) with 2 replaced by a.
cx$ b *x, x c$ or ! x $
c$x$ b *, x c$ or ! x $
. Therefore, f w axb
.
x$ c *x, c$ x ! or x $
$x$ c *, c$ x ! or x $
No, since the left- and right-hand derivatives at x !, are c* and *, respectively.
No, since the left- and right-hand derivatives at x $, are c") and "), respectively.
No, since the left- and right-hand derivatives at x c$, are ") and c"), respectively.
The critical points occur when f w axb ! (at x $) and when f w axb is undefined (at x ! and x $). The
68. Note that faxb
(a)
(b)
(c)
(d)
minimum value is ! at x c$, at x !, and at x $; local maxima occur at c$ '$ and $ '$.
Copyright 2010 Pearson Education, Inc. Publishing as Addison-Wesley.
Section 4.1 Extreme Values of Functions
"#
f w (x)
"
#
ax# b
c"#
(2x)
x
ax b
#" #
69. Yes, since f(x) kxk x# ax# b
x
kx k
177
is not defined at x 0. Thus it is
not required that f w be zero at a local extreme point since f w may be undefined there.
70. If f(c) is a local maximum value of f, then f(x) f(c) for all x in some open interval (a b) containing c. Since f is even,
f(cx) f(x) f(c) f(cc) for all cx in the open interval (cb ca) containing cc. That is, f assumesa local maximum at
the point cc. This is also clear from the graph of f because the graph of an even function is symmetric about the y-axis.
71. If g(c) is a local minimum value of g, then g(x) g(c) for all x in some open interval (a b) containing c. Since g is odd,
g(cx) cg(x) cg(c) g(cc) for all cx in the open interval (cb ca) containing cc. That is, g assumes a local
maximum at the point cc. This is also clear from the graph of g because the graph of an odd function is symmetric about
the origin.
72. If there are no boundary points or critical points the function will have no extreme values in its domain. Such functions do
indeed exist, for example f(x) x for c_ x _. (Any other linear function f(x) mx b b with m 0 will do as
well.)
73. (a) Vaxb "'!x c &#x# b %x$
Vw axb "'! c "!%x b "#x# %ax c #ba$x c #!b
The only critical point in the interval a! &b is at x #. The maximum value of Vaxb is 144 at x #.
(b) The largest possible volume of the box is 144 cubic units, and it occurs when x # units.
74. (a) f w axb $ax# b #bx b c is a quadratic, so it can have 0, 1, or 2 zeros, which would be the critical points of f. The
function faxb x$ c $x has two critical points at x c" and x ". The function faxb x$ c " has one critical point
at x ! The function faxb x$ b x has no critical points.
(b) The function can have either two local extreme values or no extreme values. (If there is only one critical point, the
cubic function has no extreme values.)
cgt b v! ! t
Thus s v c " g v b v0 v b s0
#
g
g
g
v
g
. Now satb s0 tc gt b v0 0 t 0 or t
2
b s0 s0 is the maximum height over the interval 0 t
! tan t " t
never negative) the peak current is ## amps.
dI
dt
c#sin t b #cos t, solving
76.
v2
2g
!
ds
dt
75. s c " gt# b v! t b s!
#
dI
dt
1
%
2v0
g .
2v0
g .
b n1 where n is a nonnegative integer (in this exercise t is
77. Maximum value is 11 at x 5;
minimum value is 5 on the interval c3 2;
local maximum at ac5 9b
Copyright 2010 Pearson Education, Inc. Publishing as Addison-Wesley.
178
Chapter 4 Applications of Derivatives
78. Maximum value is 4 on the interval 5 7;
minimum value is c4 on the interval c2 1.
79. Maximum value is 5 on the interval 3 _;
minimum value is c5 on the interval c_ c2.
80. Minimum value is 4 on the interval c" $
81-86. Example CAS commands:
Maple:
with(student):
f := x -> x^4 - 8*x^2 + 4*x + 2;
domain := x=-20/25..64/25;
plot( f(x), domain, color=black, title="Section 4.1 #81(a)" );
Df := D(f);
plot( Df(x), domain, color=black, title="Section 4.1 # 81(b)" )
StatPt := fsolve( Df(x)=0, domain )
SingPt := NULL;
EndPt := op(rhs(domain));
Pts :=evalf([EndPt,StatPt,SingPt]);
Values := [seq( f(x), x=Pts )];
Maximum value is 2.7608 and occurs at x=2.56 (right endpoint).
%
Minimum value $ is -6.2680 and occurs at x=1.86081 (singular point).
Mathematica: (functions may vary) (see section 2.5 re. RealsOnly ):
<<Miscellaneous `RealOnly`
Clear[f,x]
a = c1; b = 10/3;
Copyright 2010 Pearson Education, Inc. Publishing as Addison-Wesley.
Section 4.2 The Mean Value Theorem
179
f[x_] =2 b 2x c 3 x2/3
f'[x]
Plot[{f[x], f'[x]}, {x, a, b}]
NSolve[f'[x]==0, x]
{f[a], f[0], f[x]/.%, f[b]//N
In more complicated expressions, NSolve may not yield results. In this case, an approximate solution (say 1.1 here)
is observed from the graph and the following command is used:
FindRoot[f'[x]==0,{x, 1.1}]
4.2 THE MEAN VALUE THEOREM
2. When f(x) x#$ for 0 x 1, then
3. When f(x) x b
"
x
for
"
#
fa1b c fa0b
1c0
x 2, then
fa3b c fa1b
3c1
5. When f(x) x3 c x2 for c1 x 2, then
1.22 and
1 c 7
3
"
f w acb 3 2c b 2 c # .
2
f w acb 1 3 cc"$ c
fa2b c fa12b
2 c 1 2
4. When f(x) x c 1 for 1 x 3, then
1 b 7
3
fa1b c fa0b
1c0
f w acb 0 " c
f w acb
fa2b c fac1b
2 c ac1b
2
#
"
c
1. When f(x) x# b 2x c 1 for 0 x 1, then
8
#7 .
c 1.
"
# c c 1
3
c #.
f w acb 2 3c2 c 2c c
1 7
.
3
c0.549 are both in the interval c1 x 2.
x3 c2 x 0
2 cg c
, then ga2bc aca2b2b g w acb 3 g w acb. If c2 x 0, then gw (x) 3x2 3 g w acb
x2 ! x 2
3c2 3 c 1. Only c c1 is in the interval. If ! x 2, then gw (x) 2x 3 g w acb 2c 3 c 3 .
2
6. When g(x)
7. Does not; f(x) is not differentiable at x 0 in (c" 8).
8. Does; f(x) is continuous for every point of [0 1] and differentiable for every point in (0 1).
9. Does; f(x) is continuous for every point of [0 1] and differentiable for every point in (0 1).
10. Does not; f(x) is not continuous at x 0 because lim f(x) 1 0 f(0).
c
x!
11. Does not; f is not differentiable at x c1 in (c2 0).
12. Does; f(x) is continuous for every point of [0 3] and differentiable for every point in (0 3).
lim f(x) lim x 1 0 f(1).
c
x1
x1
13. Since f(x) is not continuous on 0 x 1, Rolle's Theorem does not apply:
14. Since f(x) must be continuous at x 0 and x 1 we have lim f(x) a f(0) a 3 and
b
x!
lim f(x) lim f(x) c1 b 3 b a m b b 5 m b b. Since f(x) must also be differentiable at
x1
x1
x 1 we have lim f w (x) lim f w (x) c2x b 3k x=1 mk x=1 1 m. Therefore, a 3, m 1 and b 4.
x1
x1
Copyright 2010 Pearson Education, Inc. Publishing as Addison-Wesley.
180
Chapter 4 Applications of Derivatives
15. (a) i
ii
iii
iv
(b) Let r" and r# be zeros of the polynomial P(x) xn b an-1 xn-1 b b a" x b a! , then P(r" ) P(r# ) 0.
Since polynomials are everywhere continuous and differentiable, by Rolle's Theorem Pw (r) 0 for some r
between r" and r# , where Pw (x) nxn-1 b (n c 1) an-1 xn-2 b b a" .
16. With f both differentiable and continuous on [a b] and f(r" ) f(r# ) f(r$ ) 0 where r" , r# and r$ are in [a b],
then by Rolle's Theorem there exists a c" between r" and r# such that f w (c" ) 0 and a c# between r# and r$
such that f w (c# ) 0. Since f w is both differentiable and continuous on [a b], Rolle's Theorem again applies and
we have a c$ between c" and c# such that f ww (c$ ) 0. To generalize, if f has nb1 zeros in [a b] and f n is
continuous on [a b], then f n has at least one zero between a and b.
17. Since f ww exists throughout [a b] the derivative function f w is continuous there. If f w has more than one zero in [a b], say
f w (r" ) f w (r# ) 0 for r" r# , then by Rolle's Theorem there is a c between r" and r# such that f ww (c) 0, contrary to
f ww 0 throughout [a b]. Therefore f w has at most one zero in [a b]. The same argument holds if f ww 0 throughout [a b].
18. If f(x) is a cubic polynomial with four or more zeros, then by Rolle's Theorem f w (x) has three or more zeros, f ww (x) has 2 or
more zeros and f www (x) has at least one zero. This is a contradiction since f www (x) is a non-zero constant when f(x) is a cubic
polynomial.
19. With f(c2) 11 0 and f(c1) c1 0 we conclude from the Intermediate Value Theorem that f(x) x% b 3x b 1
has at least one zero between c2 and c1. Then c2 x c1 c) x$ c1 c32 4x$ c4
c29 4x$ b 3 c1 f w (x) 0 for c2 x c1 f(x) is decreasing on [c# c1] f(x) 0 has exactly one
solution in the interval (c# c1).
4
x
b 7 f w (x) 3x# c
8
x
20. f(x) x$ b
0 on (c_ 0) f(x) is increasing on (c_ 0). Also, f(x) 0 if x c2 and
f(x) 0 if c2 x 0 f(x) has exactly one zero in (c_ !).
21. g(t) t b t b 1 c 4 gw (t)
"
# t
"
2tb1
0 g(t) is increasing for t in (! _); g(3) 3 c 2 0 and
g(15) 15 0 g(t) has exactly one zero in (! _)
"
"ct
b 1 b t c 3.1 gw (t)
"
("ct)
22. g(t)
"
2 1 bt
0 g(t) is increasing for t in (c1 1); g(c0.99) c2.5 and
g(0.99) 98.3 g(t) has exactly one zero in (c1 1).
)
2
)
)
23. r()) ) b sin# 3 c 8 rw ()) 1 b 3 sin 3 cos 3 1 b " sin 23) 0 on (c_ _) r()) is increasing on
3
(c_ _); r(0) c8 and r(8) sin# 8 0 r()) has exactly one zero in (c_ _).
3
24. r()) 2) c cos# ) b 2 rw ()) 2 b 2 sin ) cos ) 2 b sin 2) 0 on (c_ _) r()) is increasing on (c_ _);
r(c#1) c41 c cos (c#1) b 2 c41 c 1 b 2 0 and r(21) 41 c 1 b 2 0 r()) has exactly one zero in
(c_ _).
b 5 rw ()) (sec ))(tan )) b )3 0 on ! 1 r()) is increasing on ! 1 ; r(0.1) c994 and
#
#
r(1.57) 1260.5 r()) has exactly one zero in ! 1 .
#
"
)
25. r()) sec ) c
Copyright 2010 Pearson Education, Inc. Publishing as Addison-Wesley.
Section 4.2 The Mean Value Theorem
181
26. r()) tan ) c cot ) c ) rw ()) sec# ) b csc# ) c 1 sec# ) b cot# ) 0 on ! 1 r()) is increasing on 0 1 ;
#
#
r 1 c 1 0 and r(1.57) 1254.2 r()) has exactly one zero in ! 1 .
4
4
#
27. By Corollary 1, f w (x) 0 for all x f(x) C, where C is a constant. Since f(c1) 3 we have C 3 f(x) 3 for
all x.
28. g(x) 2x b 5 gw (x) 2 f w (x) for all x. By Corollary 2, f(x) g(x) b C for some constant C. Then
f(0) g(0) b C 5 5 b C C 0 f(x) g(x) 2x b 5 for all x.
29. g(x) x# gw (x) 2x f w (x) for all x. By Corollary 2, f(x) g(x) b C.
(a) f(0) 0 0 g(0) b C 0 b C C 0 f(x) x# f(2) 4
(b) f(1) 0 0 g(1) b C 1 b C C c1 f(x) x# c 1 f(2) 3
(c) f(c2) 3 3 g(c2) b C 3 4 b C C c1 f(x) x# c 1 f(2) 3
30. g(x) mx gw (x) m, a constant. If f w (x) m, then by Corollary 2, f(x) g(x) b b mx b b where b is a constant.
Therefore all functions whose derivatives are constant can be graphed as straight lines y mx b b.
bC
(b) y
32. (a) y x# b C
x
3
x
#
bC
(b) y x# c x b C
33. (a) yw cxc# y
"
x
bC
(b) y x b
"
x
35. (a) y c " cos 2t b C
#
(c) y c
cos 2t b 2 sin
(c) y 5x c
(b) y 2 sin
t
#
bC
"
x
bC
(b) y 2x b C
"
#
"
#
x
4
(c) y x$ b x# c x b C
bC
xc"# y x"# b C y x b C
(c) y 2x# c 2x b C
34. (a) yw
(c) y
31. (a) y
bC
t
#
bC
(b) yw )"# y
36. (a) y tan ) b C
2
3
)$# b C
(c) y
2
3
)$# c tan ) b C
37. f(x) x# c x b C; 0 f(0) 0# c 0 b C C 0 f(x) x# c x
"
"
38. g(x) c " b x# b C; 1 g(c1) c c1 b (c1)# b C C c1 g(x) c x b x# c 1
x
39. r()) 8) b cot ) b C; 0 r 1 8 1 b cot 1 b C 0 21 b 1 b C C c21 c 1
4
4
4
r()) 8) b cot ) c 21 c 1
40. r(t) sec t c t b C; 0 r(0) sec (0) c 0 b C C c1 r(t) sec t c t c 1
41. v
ds
dt
*)t b & s %*t# b &t b C; at s "! and t ! we have C "! s %*t# b &t b "!
42. v
ds
dt
$#t c # s "'t# c #t b C; at s % and t
43. v
ds
dt
"
sina1tb s c 1 cosa1tb b C; at s ! and t ! we have C
44. v
ds
dt
2
1 cos #t s sin #t b C; at s " and t 1# we have C " s sin #t b "
1
1
1
"
#
we have C " s "'t# c #t b "
"
1
" c cosa1tb
1
Copyright 2010 Pearson Education, Inc. Publishing as Addison-Wesley.
182
Chapter 4 Applications of Derivatives
45. a $# v $#t b C" ; at v #! and t ! we have C" #! v $#t b #! s "'t# b #!t b C# ; at s & and
t ! we have C# & s "'t# b #!t b &
46. a 9.8 v 9.8t b C" ; at v c$ and t ! we have C" c$ v *)t c $ s %*t# c $t b C# ; at s ! and
t ! we have C# ! s %*t# c $t
47. a c%sina#tb v #cosa#tb b C" ; at v # and t ! we have C" ! v #cosa#tb s sina#tb b C# ; at s c$
and t ! we have C# c$ s sina#tb c $
$
$
cos $t v 1 sin $t b C" ; at v ! and t ! we have C" ! v 1 sin $t s ccos $t b C# ; at
1
1
1
1
$t
s c" and t ! we have C# ! s ccos 1
*
1
48. a
49. If T(t) is the temperature of the thermometer at time t, then T(0) c19 C and T(14) 100 C. From the Mean Value
Theorem there exists a 0 t! 14 such that
T(14) c T(0)
14 c 0
8.5 C/sec Tw (t! ), the rate at which the temperature was
changing at t t! as measured by the rising mercury on the thermometer.
50. Because the trucker's average speed was 79.5 mph, by the Mean Value Theorem, the trucker must have been going that
speed at least once during the trip.
51. Because its average speed was approximately 7.667 knots, and by the Mean Value Theorem, it must have been going that
speed at least once during the trip.
52. The runner's average speed for the marathon was approximately 11.909 mph. Therefore, by the Mean Value Theorem, the
runner must have been going that speed at least once during the marathon. Since the initial speed and final speed are both 0
mph and the runner's speed is continuous, by the Intermediate Value Theorem, the runner's speed must have been 11 mph
at least twice.
53. Let d(t) represent the distance the automobile traveled in time t. The average speed over 0 t 2 is
d(2) c d(0)
#c0 .
Value Theorem says that for some 0 t! 2, d (t! )
d(2) c d(0)
#c0 .
The Mean
The value d (t! ) is the speed of the automobile at time t!
(which is read on the speedometer).
54. aatb vw atb "' vatb "'t b C; at a! !b we have C ! vatb "'t. When t $!, then va$!b %) m/sec.
ca
bca
c
c c" c# a ab b a c b c ab.
"
56. The conclusion of the Mean Value Theorem yields
b ca
bca
"
b
55. The conclusion of the Mean Value Theorem yields
2c c
a bb
# .
57. f w (x) [cos x sin (x b 2) b sin x cos (x b 2)] c 2 sin (x b 1) cos (x b 1) sin (x b x b 2) c sin 2(x b 1)
sin (2x b 2) c sin (2x b 2) 0. Therefore, the function has the constant value f(0) csin# 1 c0.7081
which explains why the graph is a horizontal line.
58. (a) faxb ax b #bax b "bxax c "bax c #b x& c &x$ b %x is one possibility.
Copyright 2010 Pearson Education, Inc. Publishing as Addison-Wesley.
You might also like
- Ism T12 Pre Vi PDFDocument0 pagesIsm T12 Pre Vi PDFcamauro30No ratings yet
- Calculo ThomasDocument14 pagesCalculo ThomasDaniel Valenzuela YevenesNo ratings yet
- Ismt12 C01 C PDFDocument10 pagesIsmt12 C01 C PDFCamila Ignacia LaÜesunacaritasonriendoNo ratings yet
- Ismt12 C11 BDocument0 pagesIsmt12 C11 Bhd1123No ratings yet
- Ismt12 C01 B PDFDocument6 pagesIsmt12 C01 B PDFCamila Ignacia LaÜesunacaritasonriendoNo ratings yet
- Chapter 1 Functions - Thomas Calculus 12th EditionDocument12 pagesChapter 1 Functions - Thomas Calculus 12th Editionfudge5391% (11)
- Section 6.6 Moments and Centers of Mass 369Document0 pagesSection 6.6 Moments and Centers of Mass 369Umut özdemirNo ratings yet
- Ism T12 Pre Vi PDFDocument0 pagesIsm T12 Pre Vi PDFcamauro30No ratings yet
- Ismt12 C05 ADocument0 pagesIsmt12 C05 AUmut özdemirNo ratings yet
- ISM ThomasCalc WeirHass PDFDocument2 pagesISM ThomasCalc WeirHass PDFCamila Ignacia LaÜesunacaritasonriendoNo ratings yet
- Ismt12 C09 BDocument0 pagesIsmt12 C09 Bhd1123No ratings yet
- Section 4.5 Applied Optimization 227Document0 pagesSection 4.5 Applied Optimization 227Umut özdemirNo ratings yet
- Section 5.3 The Definite Integral 275Document0 pagesSection 5.3 The Definite Integral 275Umut özdemirNo ratings yet
- 346 Chapter 6 Applications of Definite IntegralsDocument0 pages346 Chapter 6 Applications of Definite IntegralsUmut özdemirNo ratings yet
- 122 Chapter 3 DifferentiationDocument0 pages122 Chapter 3 DifferentiationUmut özdemir100% (1)
- Thomas Calculus SolutionDocument13 pagesThomas Calculus Solutionong062550% (6)
- Section 4.2 The Mean Value Theorem 183Document0 pagesSection 4.2 The Mean Value Theorem 183hd1123No ratings yet
- Shoe Dog: A Memoir by the Creator of NikeFrom EverandShoe Dog: A Memoir by the Creator of NikeRating: 4.5 out of 5 stars4.5/5 (537)
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeFrom EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeRating: 4 out of 5 stars4/5 (5794)
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceFrom EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceRating: 4 out of 5 stars4/5 (890)
- The Yellow House: A Memoir (2019 National Book Award Winner)From EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Rating: 4 out of 5 stars4/5 (98)
- The Little Book of Hygge: Danish Secrets to Happy LivingFrom EverandThe Little Book of Hygge: Danish Secrets to Happy LivingRating: 3.5 out of 5 stars3.5/5 (399)
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryFrom EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryRating: 3.5 out of 5 stars3.5/5 (231)
- Never Split the Difference: Negotiating As If Your Life Depended On ItFrom EverandNever Split the Difference: Negotiating As If Your Life Depended On ItRating: 4.5 out of 5 stars4.5/5 (838)
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureFrom EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureRating: 4.5 out of 5 stars4.5/5 (474)
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersFrom EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersRating: 4.5 out of 5 stars4.5/5 (344)
- Grit: The Power of Passion and PerseveranceFrom EverandGrit: The Power of Passion and PerseveranceRating: 4 out of 5 stars4/5 (587)
- On Fire: The (Burning) Case for a Green New DealFrom EverandOn Fire: The (Burning) Case for a Green New DealRating: 4 out of 5 stars4/5 (73)
- The Emperor of All Maladies: A Biography of CancerFrom EverandThe Emperor of All Maladies: A Biography of CancerRating: 4.5 out of 5 stars4.5/5 (271)
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaFrom EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaRating: 4.5 out of 5 stars4.5/5 (265)
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreFrom EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreRating: 4 out of 5 stars4/5 (1090)
- Team of Rivals: The Political Genius of Abraham LincolnFrom EverandTeam of Rivals: The Political Genius of Abraham LincolnRating: 4.5 out of 5 stars4.5/5 (234)
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyFrom EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyRating: 3.5 out of 5 stars3.5/5 (2219)
- The Unwinding: An Inner History of the New AmericaFrom EverandThe Unwinding: An Inner History of the New AmericaRating: 4 out of 5 stars4/5 (45)
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)From EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Rating: 4.5 out of 5 stars4.5/5 (119)
- Her Body and Other Parties: StoriesFrom EverandHer Body and Other Parties: StoriesRating: 4 out of 5 stars4/5 (821)