TAREA de Espacios Vectoriales Folleto

ESPACIOS VECTORIALES Y TRANSFORMACIONES LINEALES
Elaborado : ROGER ALBERTO GARCIA GUEVARA Pgina 1

El espacio R
n
.
Def. Si n es un entero positivo, entonces, una n-upla o n-ada ordenada es una sucesin de
nmeros reales ) , ... , , (
2 1 n
u u u . El conjunto de las n-uplas ordenadas se conoce como
espacio n-dimensional y se denota por R
n
.
De igual forma que en R
2
y R
3
) , , ( ) , (
3 2 1 2 1
u u u y u u se utilizaban para representar un punto
o un vector con punto inicial en el origen de coordenadas, la n-upla ordenada
) , ... , , (
2 1 n
u u u se puede concebir como un punto generalizado o un vector generalizado.
As, por ejemplo (-2, 1, 0, 4) se puede ver como un punto en R
4
o un vector en R
4
.
Def. Dos vectores ) , ... , , (
2 1 n
u u u u = y ) , ... , , (
2 1 n
v v v v = en R
n
son iguales si y slo si
n n
v u v u v u = = = , ... , ,
2 2 1 1
.
Las operaciones con vectores en R
n
son similares a las operaciones con vectores en R
2
y R
3
,
as:
) , ... , , (
2 2 1 1 n n
v u v u v u v u + + + = + , ) , ... , , (
2 1 n
u k u k u k u k = donde k es un escalar.
Estas operaciones son denominadas operaciones estndar en R
n
. El vector cero en R
n
se
define como ) 0 ..., , 0 , 0 ( 0 = y el negativo del vector u se define como
) , ... , , (
2 1 n
u u u u = . La diferencia de dos vectores se define como
) , ... , , (
2 2 1 1 n n
v u v u v u v u = . Las propiedades de estas operaciones son similares a
las propiedades de las operaciones con vectores en R
2
y R
3
.
Tambin puede generalizarse el concepto de magnitud y de producto punto.
De esta manera:
2 2
2
2
1
...
n
u u u u + + + = y
n n
v u v u v u v u + + + = ... .
2 2 1 1
siendo ) , ... , , (
2 1 n
u u u u = y
) , ... , , (
2 1 n
v v v v = . De igual manera que la suma y el producto escalar-vector, las
propiedades de la magnitud y el producto punto son similares a las de la magnitud y
producto punto en el plano y el espacio.
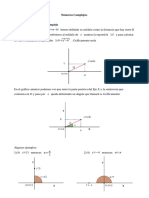
Por ejemplo, el ngulo entre vectores est dado por : cos . v u v u =
Ejemplo. Dados los vectores de R
4
) 0 , 7 , 4 , 5 ( ) 7 , 5 , 3 , 1 ( = = v y u , hallar:
a) v u 3 2 , b) el ngulo entre v y u .
Solucin. a) Primeramente multiplicamos por los escalares
) 0 , 21 , 12 , 15 ( 3 ) 14 , 10 , 6 , 2 ( 2 = = v y u .
Realizando la diferencia tenemos que:
) 14 , 11 , 18 , 17 ( ) 0 , 21 , 12 , 15 ( ) 14 , 10 , 6 , 2 ( 3 2 = = v u
Extrayendo magnitud, se tiene que:
v u 3 2
2 2 2 2
14 ) 11 ( 18 ) 17 ( + + + = 5 . 30 930 ~ =
b) Extraemos primeramente el producto punto:
20 35 12 3 ) 0 )( 7 ( ) 7 )( 5 ( ) 4 ( ) 3 ( ) 3 )( 1 ( ) 0 , 7 , 4 , 5 ( . ) 7 , 5 , 3 , 1 ( . = + = + + + = = v u
Ahora calculamos la magnitud de cada uno de los vectores:
84 7 5 3 ) 1 (
2 2 2 2
= + + + = u y 90 0 7 ) 4 ( 5
2 2 2 2
= + + + = v
De esta forma; 23 . 0
90 84
20
cos ~ = y
0 1
7 . 76 ) 23 . 0 ( cos ~ =

ESPACIOS VECTORIALES GENERALES.

Un espacio vectorial real V es un conjunto de objetos llamados vectores, junto con dos
operaciones llamadas suma de vectores y producto de un vector por un escalar que
satisfacen los diez axiomas enumerados a continuacin.
Si V w v u e , , y escalares R l k e , :
i) V v u e +
ii) u v v u + = +
iii) w v u w v u + + = + + ) ( ) (
iv) u u u V u todo para que tal V = + = + e e - 0 0 , 0
v) 0 ) ( ; = + = + e - e u u u u que tal V u V u
vi) V u k e
vii) u l u k u l k + = + ) (
viii) v k u k v u k + = + ) (
ix) u l k u l k ) ( ) ( =
x) u u = 1
Ejemplos de espacios vectoriales.
1) El conjunto de vectores en R
n
con las operaciones suma de vectores en R
n
y el
producto de un vector en R
n
por un escalar.
2) El conjunto de matrices de orden m x n M
mxn
con las operaciones suma de matrices
y producto de una matriz por un escalar.
3) El conjunto de polinomios de grado menor o igual a n, P
n
, con las operaciones suma
de polinomios y producto de un polinomio por un nmero.
4) El conjunto de funciones de variable real con las operaciones suma de funciones y
producto de una funcin por un nmero real.
Ejemplo de un espacio trivial. El conjunto que contiene solamente al vector cero o nulo,
es decir, } 0 { = V . Este espacio recibe el nombre de espacio trivial o espacio cero.
Ejemplo. Todo plano en R
3
que pasa por el origen es un espacio vectorial con las
operaciones suma de vectores y producto de un escalar por un vector en R
3
.
Solucin. Ya que los vectores del plano son vectores de R
3
las propiedades asociativas,
conmutativas son obvias, por lo tanto, bastar probar los axiomas; i, iv, v y vi.
i) Como todo plano que pasa por el origen tiene ecuacin 0 = + + cz by ax todo
vector del plano debe satisfacer dicha ecuacin. Sean ) , , (
3 2 1
u u u u = y
) , , (
3 2 1
v v v v = vectores del plano dado, entonces, 0
3 2 1
= + + cu bu au y
0
3 2 1
= + + cv bv av , sumando las dos igualdades anteriores y sacando factor
comn se tiene que: 0 ) ( ) ( ) (
3 3 2 2 1 1
= + + + + + v u c v u b v u a y de esta forma se
tiene que v u v u v u v u + = + + + ) , , (
3 3 2 2 1 1
satisface la ecuacin, por lo que
existe cerradura con respecto a la suma.
iv) El vector ) 0 , 0 , 0 ( 0 = satisface la ecuacin 0 = + + cz by ax , as que, todo plano
que pasa por el origen contiene al vector cero.
v) Si ) , , (
3 2 1
u u u u = est en el plano, entonces, 0
3 2 1
= + + cu bu au , lo que es
equivalente a la ecuacin 0 ) ( ) ( ) (
3 2 1
= + + u c u b u a y de esta forma el vector
) , , (
3 2 1
u u u u = tambin est en el plano, as que el plano que pasa por el
origen cumple con la ley del vector opuesto.
vi) Si ) , , (
3 2 1
u u u u = est en el plano, entonces, 0
3 2 1
= + + cu bu au , lo que es
equivalente a la ecuacin 0
3 2 1
= + + cu k bu k au k que tambin puede escribirse
como 0 ) ( ) ( ) (
3 2 1
= + + ku c ku b ku a y por lo tanto, el vector
) , , (
3 2 1
ku ku ku u k = tambin est en el plano.
As vemos pues, que se cumplen todos los axiomas, y por lo tanto todo plano del espacio
R
3
que pasa por el origen forma un espacio vectorial con las operaciones ya definidas.
Ejemplo. D una razn por la cual el conjunto } 0 , 0 / ) , ( { > > = y x y x W no es un
espacio vectorial con las operaciones en R
2
.
Solucin: No se cumple el axioma del opuesto, puesto que el conjunto dado solamente
contiene los vectores de R
2
situados en el primer cuadrante, desde el punto de vista
geomtrico, as que, los opuestos de estos vectores estarn en el tercer cuadrante, lo cual
no forma parte del conjunto.
De otra forma: Si , ) , (
2 1
W u u u e = entonces, W u u u e = ) , (
2 1
.
Teorema 1. Sea V un espacio vectorial, entonces:
i. 0 0 = k para todo escalar k
ii. 0 0 = v para todo V v e
iii. Si 0 = v k entonces, 0 = k 0 = v ( o ambos)
iv. u u = ) 1 (
Ejercicios propuestos.
1. En los siguientes ejercicios se da un conjunto de objetos con las operaciones adicin y
multiplicacin por un escalar. Determinar cuales de ellos son espacios vectoriales bajo
las operaciones dadas:
a) El conjunto de todas las ternas de nmeros reales (x,y,z ) con las operaciones (x,y,z)
+(x, y, z) = (x + x, y + y, z+ z) y k(x, y, z) = (kx, ky,kz)
b) El conjunto de todas las parejas de nmeros reales de la forma (x, y) donde x > 0,
con las operaciones estndar en R
2
.
c) El conjunto de las matrices de orden 2 x 2 cuyos elementos en la diagonal
secundaria son 1, con la adicin matricial y la multiplicacin por un escalar.
d) El conjunto de las funciones de valor real definidas en todo punto de la recta tal que
f(1) = 0 con las operaciones con funciones tradicionales.
e) El conjunto de los polinomios de la forma P(x) = a
0
+ a
1
x + a
2
x
2
+ ... + a
n
x
n
2. .Demostrar el teorema 1.
3. Mostrar que para todo escalar k y vectores v y u , v k u k v u k = ) (
4. Demostrar que toda recta en R
2
que pasa por el origen es un espacio vectorial con las
operaciones suma de vectores y producto de un vector por un escalar en R
2
.
5. Repita el ejercicio 4 para una recta que pasa por el origen en R
3
.
6. Puede un espacio vectorial componerse: 1) de un solo vector; 2) de dos vectores
diferentes?
7. A partir de un espacio vectorial ha sido eliminado el vector x. Puede el conjunto de los
vectores obtenido despus de esta eliminacin quedarse como espacio vectorial?
8. Cada da llegan a Peas Blancas (frontera CR-Nicaragua) camiones de diferente tipo:
furgones de carga, coches de tercera, segunda y primera clase, a partir de los cuales se
forman diariamente y salen buses de pasajeros ordinarios y rpidos. Sean
5 4 3 2 1
, , , , los incrementos diarios del nmero de camiones respectivos. Es el
conjunto de los nmeros (
5 4 3 2 1
, , , , ) un espacio vectorial?
9. Demostrar que el conjunto de todas las soluciones de un sistema de ecuaciones lineales
homogneas
= + +
= + +
0
0
2 2 2
1 1 1
z c y b x a
z c y b x a
forma un espacio vectorial.
SUBESPACIOS VECTORIALES.
Un subconjunto W de un espacio vectorial V es un subespacio de V, si W es a s mismo un
espacio vectorial bajo la adicin y producto escalar definidos sobre V .
Ejemplos. Las rectas y planos que pasan por el origen en R
3
son subespacios vectoriales de
R
3
.
Teorema 2: Si W es un conjunto de uno o ms vectores de V , entonces, W es un
subespacio de V si y slo si se cumplen las condiciones siguientes:
i) Si W v u W v u e + e , ,
ii) Si k es un escalar cualquiera y , W u e entonces, W u k e
Ejemplo. Sea W el conjunto de las matrices de la forma
|
|
.
|
\
|
0
0
21
12
a
a
. Determinar si W es
un subespacio del espacio de matrices M
2 x 2
.
Sean W B A e , , entonces,
|
|
.
|
\
|
=
|
|
.
|
\
|
=
0
0
0
0
21
12
21
12
b
b
B y
a
a
A , as:
i. W
b a
b a
b a
b a
B A e
|
|
.
|
\
|
+
+
=
|
|
.
|
\
|
+ +
+ +
= +
0
0
0 0
0 0
21 21
12 12
21 21
12 12

ii. Sea W
a k
a k
a
a
k A k R k e
|
|
.
|
\
|
=
|
|
.
|
\
|
= e
0
0
0
0
;
21
12
21
12
Por lo tanto, se cumplen ambas condiciones del teorema 2, as que el conjunto W
es un
subespacio del espacio M
2 x 2
.
Nota: Todo espacio vectorial tiene al menos dos subespacios, el espacio propio y el espacio
cero.
Ejemplo. Demostrar que el conjunto de las funciones continuas en todo R es un subespacio
de F, el espacio de las funciones de variable real.
Solucin. Sean W x g x f e ) ( ), ( , donde
W
es el conjunto de las funciones continuas en
toda la recta numrica. De esta forma, por las propiedades de las funciones continuas, se
tiene que:
i. W x g x f x g f e + = + ) ( ) ( ) ( ) ( ya que la suma de dos funciones continuas en toda
la recta numrica tambin es continua.
ii. Sea
k
un escalar cualquiera, entonces, tambin por las propiedades de las
funciones continuas ) ( ) ( ) ( x f k x f k = tambin es continua.
Por lo tanto el conjunto de las funciones continuas de variable real es un subespacio de las
funciones de variable real.
1. Cules de los siguientes conjuntos son subespacios de R
3
?
a) todos los vectores de la forma (a, 0, 0)
b) todos los vectores de la forma (a, 1, 1)
c) todos los vectores de la forma (a, b, c) con b = a + c + a
2. Cules de los siguientes subconjuntos de M
2 x 2
son subespacios de M
2 x 2
?
a) las matrices cuyos elementos son nmeros enteros
b) las matrices cuyos elementos en la diagonal principal suman cero
c) las matrices simtricas
d) las matrices antisimtricas
e) las matrices diagonales
f) las matrices singulares
3. Cules de los siguientes conjuntos son subespacios de los polinomios de grado
menor o igual a 3, P
3
?
a) los polinomios cuyo trmino independiente es cero
b) los polinomios cuya suma de sus coeficientes sea cero
4. Sea A X = 0, un sistema homogneo de ecuaciones donde A es una matriz de orden
m x n, X es un vector en R
n
y B un vector de R
m
. Determinar si el conjunto de
soluciones de este sistema es un subespacio de R
n
. Es vlida la conclusin anterior
si el sistema admite solamente la solucin trivial? Explique su respuesta.
5. Investigue si el conjunto } 2 : ) , , , ( {
4
d b a R d c b a S = e = es un subespacio de R
4
.
6. Determine cuales de los conjuntos son cerrados bajo las operaciones indicadas.
a. El conjunto de todas las matrices diagonales n x n respecto a la suma de
matrices y la multiplicacin por escalar.
b. El conjunto de todas las matrices triangulares superiores de n x n con respecto a
la adicin y la multiplicacin por escalar.
c. El conjunto S de todas las matrices de la forma
|
|
.
|
\
|
a b
b a
, en donde a y b son
nmeros reales, con la operacin de adicin de matrices y multiplicacin por un
escalar.
d. El conjunto de vectores en R
3
de la forma (x, x, x).
e. El conjunto de matrices simtricas de n x n bajo la suma y multiplicacin por
escalar.
f. El conjunto de matrices 2 x 2 que tienen la forma
|
|
.
|
\
|
0
0
b
a
bajo la suma y
multiplicacin por un escalar.
g. El conjunto de puntos en R
3
que estn sobre la recta x = t + 1, y = 2t, z = t 1.
7. Determine si el subconjunto dado H del espacio vectorial V es un subespacio de V.
a. V = R
2
; H = {(x, y)\ x = y}.
b. V = R
2
; H = { (x, y )\ x
2
+ y
2
s1}
c. V = M
n x n
; H = {T e M
n x n
, T es A superior}
d. V = M
nn
; H = { S e M
nn
; S es simtrica}
e. V = M
nn
; H ={ A e M
nn
; a
ij
= 0}
f. V = M
22
; H = { A e M
22
; A =
|
|
.
|
\
|
c b
b a
}
g. V = M
22
; H = {A e M
22
; A =
|
|
.
|
\
| +
0 0
1 a a
}
h. V = P
n
; H = {P e P
n
: p(0) = 1}
i. Sea V = M
22
; H
1
= {A e M
22
; a
11
= 0} . H
2
= {A e M
22
; A =
|
|
.
|
\
|
b a
a b
}.
Demuestre que H
1
. H
2
son subespacios.
j. Sea H = {(x, y, z, w)\ ax + by + cz + dw = 0}, donde a, b, c, d e 9 , no todos
cero. Demuestre que H es un subespacio propio de R
4
. H se llama hiperplano en
R
4
, que pasa por el origen.
k. Sea H = {(x
1
, x
2
,,x
n
)\ a
1
x
1
+ a
2
x
2
+ +a
n
x
n
= 0} donde a
1
, a
2
,,a
n
e 9, no
todos ceros. Demuestre que H es un subespacio propio de R
n
, H se llama
hiperplano en R
n
.
COMBINACIN LINEAL DE VECTORES.
Un vector w de un espacio vectorial
V
es combinacin lineal de los vectores
V v v v
r
e , ... , ,
2 1
si se puede expresar en la forma
r r
v k v k v k w + + + = ...
2 2 1 1
donde
r
k k k , ... , ,
2 1
son escalares.
Ejemplo. Sean ) 2 , 4 , 6 ( ) 1 , 2 , 1 ( = = v y u , expresar los vectores
) 8 , 1 , 4 ( ) 7 , 2 , 9 ( = = z y w como combinacin lineal de los vectores v y u .
Solucin.
Primeramente, escribimos la combinacin lineal como que sta existe y formamos un
sistema de ecuaciones lineales donde las incgnitas son los escalares.
(9, 2, 7) = k
1
(1, 2, -1) + k
2
(6, 4, 2)
(9, 2, 7) = (k
1
+ 6k
2 ,
2k
1
+ 4 k
2 ,
k
1
+ 2k
2
). De esta forma se tiene el sistema de
ecuaciones siguiente:
k
1
+ 6k
2
= 9

2k
1
+ 4 k
2
= 2
k
1
+ 2k
2
= 7
Haciendo uso de la eliminacin Gaussiana, tenemos que:
|
|
|
.
|
\
|
~
|
|
|
.
|
\
|
~
|
|
|
.
|
\
|
0 0 0
16 8 0
9 6 1
16 8 0
16 8 0
9 6 1
7 2 1
2 4 2
9 6 1
de donde se obtiene el sistema
equivalente:
k
1
+ 6k
2
= 9
- 8 k
2
= - 16 de donde resulta k
1
= -3 y k
2
= 2.
Por lo tanto, la combinacin lineal es: v u w 2 3 + = .
Al siguiente vector aplicamos la misma situacin, o sea:
v c u c z
2 1
+ = lo cual nos conduce al siguiente sistema de ecuaciones:
c
1
+ 6c
2
= 4
2c
1
+ 4 c
2
= - 1
c
1
+ 2c
2
= 7 el cual el es un sistema incompatible y por lo tanto el vector z
no puede expresarse como combinacin lineal de los vectores v y u .
1. Expresar los polinomios dados como combinacin lineal de los p = 2 + x + 4x
2
, q
= 1- x + 3x
2
, r = 3 + 2x + 5x
2
:
a) 5 + 9x + 5x
2
b) 2 + 6x
2
c) 2 + 2x + 3x
2
2. Dadas las siguientes matrices:
|
|
.
|
\
|
=
|
|
.
|
\
|
=
|
|
.
|
\
|
=
2 0
2 4
4 2
1 0
3 1
2 1
C B A . Cules de
las siguientes matrices son combinacin lineal de las matrices A, B y C.
a)
|
|
.
|
\
|
|
|
.
|
\
|
|
|
.
|
\
|
0 0
0 0
)
1 5
7 1
)
8 0
3 6
c b
3. Demostrar que cualquier vector del subespacio vectorial } 0 : ) , , ( {
3
= e = a R c b a S
es una combinacin lineal del conjunto } ) 1 , 3 , 0 ( , ) 0 , 1 , 0 ( { = A subconjunto de R
3
.
4. Haciendo uso de las combinaciones lineales, balancear las siguientes ecuaciones
qumicas:
a)
3 4 2 4 2 3
HNO SO Na SO H NO Na + +
b) O H NO HIO HNO I
2 2 3 3 2
+ + +
GENERADOR Y ESPACIO GENERADO.
Si
r
v v v , ... , ,
2 1
son vectores de un espacio vectorial
V
y si todo vector en
V
es
expresable como una combinacin lineal de los vectores
r
v v v , ... , ,
2 1
, entonces, se dice
que estos vectores generan al espacio vectorial
V
.
Ejemplo. Los vectores ) 1 , 0 , 0 ( ) 0 , 1 , 0 ( ), 0 , 0 , 1 ( = = = k y j i generan a R
3
ya que todo
vector ) , , ( c b a en R
3
puede expresarse como: k c j b i a c b a + + = ) , , (
Ejemplo. Los polinomios 1, x, x
2
, ... , x
n
genera al espacio de polinomios de grado n P
n
ya que: a
0
+ a
1
x + a
2
x
2
+ ... + a
n
x
n
= a
0
(1) + a
1
(x) + a
2
(x
2
) + + a
n
(x
n
)
Ejemplo. Determine si los vectores ) 3 , 1 , 2 ( ) 1 , 0 , 1 ( , ) 2 , 1 , 1 (
3 2 1
= = = v y v v generan a R
3
.
Solucin. Se debe probar que cualquier vector de R
3
) , , ( c b a u = debe expresarse como
combinacin lineal de los vectores dados inicialmente.
De esta manera:
) 3 , 1 , 2 ( ) 1 , 0 , 1 ( ) 2 , 1 , 1 ( ) , , (
3 2 1
k k k c b a + + = lo cual nos conlleva al siguiente sistema de
ecuaciones:
= + +
= +
= + +
c k k k
b k k
a k k k
3 2 1
3 1
3 2 1
3 2
2
. La matriz de coeficientes de este sistema de ecuaciones tiene
determinante igual a cero, lo cual indica que el sistema tiene infinitas soluciones o es
incompatible.
|
|
|
.
|
\
|

~
|
|
|
.
|
\
|

~
|
|
|
.
|
\
|
a b c
a b
a
a c
a b
a
c
b
a
0 0 0
1 1 0
2 1 1
2 1 1 0
1 1 0
2 1 1
3 1 2
1 0 1
2 1 1
Esto indica que el sistema es compatible si y slo si c b- a = 0 para que los rangos de la
matriz de coeficientes y la matriz ampliada del sistema sean iguales. En este caso dicho
rango es igual a 2.
Por lo tanto, los vectores dados no generan al espacio R
3
.
En general, un conjunto de vectores de un espacio vectorial determinado puede o no
generar al espacio dado. Si no lo genera, entonces, genera a un subespacio de ste. Dicho
subespacio es el conjunto de las combinaciones lineales de los vectores dados y se llama
espacio generado que se denota por lin(S) donde S es el conjunto que contiene a los
vectores.
Pregunta para el estudiante: Qu diferencia hay entre generador y espacio generado?
Explique.
1. Determine que conjunto de vectores generan a R
3
:
a) (1, 1, 1), (2, 2, 0), (3, 0, 0)
b) (2, -1, 3), (4, 1, 2), (8, -1, 8)
c) (1, 3, 3), (1, 3, 4), (1, 4, 3), (6, 2, 1)
2. Determine si los polinomios p = 1 + 2x x
2
, q = 3 + x
2
, generan a los polinomios de
grado 2.
3. Cules de las siguientes funciones estn en el espacio que genera las funciones f(x) =
cos
2
x, g(x) = sen
2
x.
a) cos 2x b) 3 + x
2
c) 1 d) sen x
4. Demuestre que el conjunto de vectores } ) 0 , 9 , 5 ( ), 2 , 5 , 3 ( ), 1 , 2 , 1 ( { = T no genera a
R
3
y determinar el subespacio de R
3
que genera dicho conjunto.
5. En M
22
;
|
|
.
|
\
|
|
|
.
|
\
|
|
|
.
|
\
|
|
|
.
|
\
|
1 3
0 0
;
0 0
1 3
;
1 2
0 0
;
0 0
1 2
6. En M
22
;
|
|
.
|
\
|

|
|
.
|
\
|
|
|
.
|
\
|

3 1
6 7
;
5 3
9 7
;
8 8
7 2
7. Cules de los siguientes subconjuntos constituyen una base para R
4
?
8.
|
|
|
|
|
.
|
\
|
|
|
|
|
|
.
|
\
|
|
|
|
|
|
.
|
\
|
|
|
|
|
|
.
|
\
|
2
3
4
4
,
1
2
5
5
,
0
1
3
3
,
2
0
1
1
2.
|
|
|
|
|
.
|
\
|
|
|
|
|
|
.
|
\
|
|
|
|
|
|
.
|
\
|
|
|
|
|
|
.
|
\
|
1
0
2
0
,
5
3
2
1
,
0
1
1
2
,
3
2
1
3
3.
|
|
|
|
|
.
|
\
|
|
|
|
|
|
.
|
\
|
|
|
|
|
|
.
|
\
|
|
|
|
|
|
.
|
\
|
3
1
2
0
,
0
0
1
4
,
0
0
0
0
,
5
3
1
1
9. Demuestre que los polinomios, 1, 1 + x, 1 + x + x
2
, ... , 1 + x + x
2
+ ... + x
n
generan al
espacio de polinomios de grado n.
10. Demuestre que si v y u estn en } , ... , , {
2 1 k
v v v lin entonces, u k y v u + estn
en } , ... , , {
2 1 k
v v v lin .
DEPENDENCIA E INDEPENCIA LINEAL.
Sea } , ... , , {
2 1 r
v v v S = un conjunto de vectores de un espacio vectorial, la ecuacin
vectorial 0 ...
2 2 1 1
= + + +
r r
v k v k v k tiene al menos una solucin a saber,
0 ...
2 1
= = = =
r
k k k . Si sta es la nica solucin , entonces, se dice que el conjunto S es
linealmente independiente, (L. I.) . Si hay otras soluciones, se dice que el conjunto es
linealmente dependiente (L. D.).
Ejemplo. El conjunto } ) 8 , 5 , 1 , 7 ( ), 1 , 5 , 2 , 1 ( ), 3 , 0 , 1 , 2 ( {
3 2 1
= = = = v v v S es
linealmente dependiente ya que 0 3
3 2 1
= + v v v .
Ejemplo. Los polinomios
2 2
3 1 , 2 3 5 , 1 x x r x x q x p + = + = = forman un conjunto
linealmente dependiente ya que 0 2 3 = + r q p
Ejemplo. Los vectores en R
3
, k j i , , forman un conjunto linealmente independiente ya
que ) 0 , 0 , 0 ( ) 1 , 0 , 0 ( ) 0 , 1 , 0 ( ) 0 , 0 , 1 (
3 2 1
= + + k k k implica que :
0 ) 0 , 0 , 0 ( ) , , (
3 2 1 3 2 1
= = = = k k k k k k
Ejemplo. Determinar si los vectores ) 1 , 2 , 3 ( ), 1 , 6 , 5 ( ), 3 , 2 , 1 (
3 2 1
= = = v v v son
linealmente dependientes o linealmente independientes.
Solucin. Primeramente planteamos una combinacin lineal de los vectores dados y se
iguala al vector cero, esto nos conduce a un sistema de ecuaciones homogneo, el cual se
analiza si solamente admite la solucin trivial o tiene otras soluciones:
) 0 , 0 , 0 ( ) 1 , 2 , 3 ( ) 1 6 , 5 ( ) 3 , 2 , 1 (
3 2 1
= + + k k k , el sistema de ecuaciones respectivo es:
= +
= + +
= + +
0 3
0 2 6 2
0 3 5 `
3 2 1
3 2 1
3 2 1
k k k
k k k
k k k
|
|
|
.
|
\
|
~
|
|
|
.
|
\
|

~
|
|
|
.
|
\
|
0 0 0
8 16 0
3 5 1
8 16 0
8 16 0
3 5 1
1 1 3
2 6 2
3 5 1
El sistema equivalente es:
= +
= + +
0 8 16
0 3 5
3 2
3 2 1
k k
k k k
De aqu se deduce que:
3 1 3 2
2
1
2
1
k k y k k = = , as que el sistema admite infinitas
soluciones y por lo tanto, los vectores dados son linealmente dependientes.
Si un conjunto de vectores es linealmente dependiente, se tiene que:
0 ...
2 2 1 1
= + + +
r r
v k v k v k
r
r
v
k
k
v
k
k
v
k
k
v
1
3
1
3
2
1
2
1
... =
En efecto, para un conjunto de vectores linealmente dependiente, cualquiera de los
vectores puede expresarse como combinacin lineal de los vectores restantes.
Anteriormente, se expres el vector
1
v como combinacin lineal de los vectores
r
v v v , ... , ,
3 2
.
Para el caso particular de dos vectores se tiene que 0
2 2 1 1
= + v k v k o sea que
2
1
2
1
v
k
k
v = , esto es , dos vectores de un espacio vectorial son linealmente
dependientes si y slo si, uno de ellos es mltiplo escalar del otro. En caso contrario son
linealmente independientes.

Teorema: Sea } , ... , , {
2 1 r
v v v S = un conjunto de vectores en R
n
. Si r > n entonces, el
conjunto S es linealmente dependiente.
Para el caso de funciones, se puede probar la dependencia lineal a travs del determinante
denominado Wronskiano. Sean
n
f f f , ... , ,
2 1
un conjunto de funciones, entonces, el
conjunto de funciones es linealmente dependiente si:
0
....
..... .....
...
. ...
) ... , , (
) 1 ( ) 1 (
2
) 1 (
1
2 1
2 1
2 1
= =
n
n
n n
n
n
n
f f f
f f f
f f f
f f f W , en caso contrario, el conjunto es LI.
Ejemplo. El conjunto } , {
2x x
e e S= es linealmente independiente ya que:
0 2
2
) , (
3 3
2
2
2
= = =
x x
x x
x x
x x
e e
e e
e e
e e W
2
v
1
v
Linealmente dependientes
2
v
1
v
Linealmente independientes
1. Investigar si los siguientes conjuntos de vectores son linealmente dependientes o
linealmente independientes.
a) A = { (2, 1, 0, 1), (2, 3, 0, 1), (1, 0, 0, 1)}
b) B = { (1,4), (0, 1), (3, 3), (4, 7)}
c) C = { 1, 0, 4), (0, 1, 3), (1, -1, 2)}
d) F = { x
2
3x + 2, x
2
4x + 3, x
2
5x + 4}
e)
}
0 0
4 2
,
1 0
0 2
,
1 2
1 0
,
2 0
1 1
{
|
|
.
|
\
|
|
|
.
|
\
|
|
|
.
|
\
|
|
|
.
|
\
|
= L
T = { f(x)= 2x
2
+ x 1 , g(x) = x 2, h(x) = 3 }
f) R = { f(x) = 1, g(x) = cos x, h(x) = sen x}
2. Para qu valores de k los vectores que siguen forman un conjunto linealmente
dependiente? (k, -1/2, -1/2), (-1/2, k, -1/2) , (-1/2, -1/2, k).
Determinar el nmero mximo de vectores L. I de los siguientes subconjuntos
3.
|
|
.
|
\
|
|
|
.
|
\
|
|
|
.
|
\
|
0
1
,
2
4
,
1
1
2.
|
|
|
.
|
\
|
|
|
|
.
|
\
|
|
|
|
.
|
\
|
1
1
3
,
2
4
2
,
1
3
1
3.
|
|
|
|
|
.
|
\
|
|
|
|
|
|
.
|
\
|
|
|
|
|
|
.
|
\
|
|
|
|
|
|
.
|
\
|
0
4
1
2
,
1
1
0
1
,
0
1
1
0
,
1
3
1
1
3. Sea } , ... , , {
2 1 n
v v v S = un conjunto de vectores de un espacio vectorial V, Demostrar
que si uno de los vectores es el vector cero, Entonces, S es linealmente dependiente.
4. Sean v y u dos vectores linealmente independientes y sea } , { v u lin w e ,
entonces, } , , { w v u es linealmente independiente.
5. Se tiene un conjunto de 4 vectores linealmente independientes. Entonces un conjunto
formado por tres de estos vectores es L. I.? Explique. Si al conjunto de los 4 vectores LI se
le agrega otro vector arbitrario, este nuevo conjunto es LI? Explique.
BASE Y DIMENSION DE UN ESPACIO VECTORIAL.
Si V es cualquier espacio vectorial y } , ... , , {
2 1 n
v v v S = es un conjunto de vectores en
V , entonces, S es una base para V si :i) S es L. I. ii) S genera a V .
Ejemplo. El conjunto de vectores } ) 1 , 0 , 0 ( ), 0 , 1 , 0 ( ), 0 , 0 , 1 ( { = S es una base para el
espacio vectorial R
3
ya que se demostr anteriormente que este conjunto genera a R
3
y
adems se puede probar que este conjunto es linealmente independiente. Esta base es la
llamada base cannica para R
3
.
Ejemplo. El conjunto {1, x, x
2
, ... , x
n
} es la base cannica para el espacio de polinomios
de grado menor o igual a n.
Ejemplo. Las matrices
|
|
.
|
\
|
|
|
.
|
\
|
|
|
.
|
\
|
|
|
.
|
\
|
1 0
0 0
,
0 1
0 0
,
0 0
1 0
,
0 0
0 1
forman la base cannica para el
espacio de matrices de orden 2 x 2, M
2x2
.
Ejemplo. Demostrar que el conjunto } ) 4 , 3 , 3 ( ), 0 , 9 , 2 ( ), 1 , 2 , 1 ( { = S es una base para R
3
.
Solucin. Se probarn las dos condiciones de base, primeramente veamos si el conjunto
genera a R
3
.
) 4 , 3 , 3 ( ) 0 , 9 , 2 ( ) 1 , 2 , 1 ( ) , , (
3 2 1
k k k c b a + + = el cual nos conduce al sistema de ecuaciones
siguientes:
= +
= + +
= + +
c k k
b k k k
a k k k
3 1
3 2 1
3 2 1
4
3 9 2
3 2
Calculando el determinante del sistema se tiene que:
0 1
4 0 1
3 9 2
3 2 1
= = , lo que indica que el sistema tiene una nica solucin
independientemente de los valores de c y b a, . As que los vectores generan a R
3
.
Ahora veamos si el conjunto de vectores es linealmente independiente:
) 4 , 3 , 3 ( ) 0 , 9 , 2 ( ) 1 , 2 , 1 ( ) 0 , 0 , 0 (
3 2 1
c c c + + = lo cual conduce al sistema homogneo de
ecuaciones siguientes:
= +
= + +
= + +
0 4
0 3 9 2
0 3 2
3 1
3 2 1
3 2 1
c c
c c c
c c c
El determinante del sistema es el mismo del sistema anterior, por lo tanto, el sistema
solamente admite la solucin trivial, as que los vectores son linealmente independientes.
As que el conjunto dado es una base para R
3
.
Teorema. Si } , ... , , {
2 1 n
v v v S = es una base para un espacio vectorial V , entonces, todo
conjunto de ms de n vectores, es linealmente dependiente.
Ejemplo. El conjunto de vectores{ (1,2,-1), (3,5,2), (-7, 9, 0), (8, -2, 4)} es linealmente
dependiente ya que la base cannica para R
3
tiene solamente tres vectores.
Teorema. Dos bases cualesquiera tienen el mismo nmero de vectores.
Ejemplo. Para R
3
la base cannica y la base {(1,2,1), (2,9,0),(3,3,4)} tienen tres vectores
cada una.
Un espacio vectorial es de dimensin finita si tiene un conjunto finito de vectores que
forman una base.
La dimensin de un espacio vectorial } , ... , , {
2 1 n
v v v S = se define como el nmero de
vectores en una base para V . Adems, por definicin, el espacio vectorial cero tiene
dimensin cero.
As por ejemplo, se tiene que:
dim R
n
= n, dim P
n
= n + 1, dim M
m xn
= m x n, d.im F = .
Teorema.
a) Si } , ... , , {
2 1 n
v v v S = es un conjunto de n vectores que genera un espacio V de
dimensin n, entonces, S es una base para V .
b) Si } , ... , , {
2 1 n
v v v S = es un conjunto de n vectores linealmente independientes en
un espacio V de dimensin n, entonces, S es una base para V .
c) Si } , ... , , {
2 1 r
v v v S = es un conjunto de vectores linealmente independientes en
un espacio V de dimensin n, y r < n, entonces, se puede agrandar S hasta
formar una base para V , es decir, existen los vectores
n r
v v , ... ,
1 +
tal que
} ..., , , ..., , , {
1 2 1 n r r
v v v v v
+
es una base para V .
Teorema. Sean V y U dos espacios vectoriales tal que V U _ , entonces,
V U dim dim s .
Ejemplo. Determinar si los vectores ) 5 , 5 ( ) 7 , 3 ( = = v y u forman una base para R
2
.
Solucin. Los vectores son linealmente independientes ya que ninguno de ellos es mltiplo
escalar del otro y como son dos vectores y dim R
2
= 2, entonces, el conjuntos formado por
los vectores ) 5 , 5 ( ) 7 , 3 ( = = v y u forman una base para R
2
.
1. Determinar si cada uno de los siguientes conjuntos de vectores forman o no una
base para el espacio vectorial especificado:
a) {(2, 1), (-3,5)} para R
2
b) {(2, 4, -3), (0, 1, 1), (0, 1, -1)} para R
3
c) { }
1 5
7 1
,
7 5
4 2
,
5 1
1 1
,
2 4
3 1
|
|
.
|
\
|

|
|
.
|
\
|

|
|
.
|
\
|
|
|
.
|
\
|

para M
2x2
2. D una explicacin por qu los conjuntos siguientes de vectores no son bases para
los espacios vectoriales que se indican (resolver por simple inspeccin)
a) {(1,2), (0,3), (2,7)} para R
2
b) { (-1, 3 2), (6,1,1)} para R
3
c){ 1 + x + x
2
, x 1} para P
2
3. Sea V el espacio generado por los vectores f(x) = cos
2
x, g(x) = sen
2
x, h(x) = cos
2x: a) Demostrar que estos vectores no forman una base para V
b) Hallar una base para V
4. Determine las dimensiones de los siguientes subespacios de R
4
:
a) todos los vectores de la forma (a, b, c, 0)
b) todos los vectores de la forma (a,b,c,d) con a = b = c = d
5. Determine la dimensin del subespacio del espacio de los polinomios de orden 3
que consta de los polinomios cuyo trmino independiente es igual a cero.
6. Cules de los siguientes subconjuntos constituyen una base para R
4
?
|
|
|
|
|
.
|
\
|
|
|
|
|
|
.
|
\
|
|
|
|
|
|
.
|
\
|
|
|
|
|
|
.
|
\
|
2
3
4
4
,
1
2
5
5
,
0
1
3
3
,
2
0
1
1
2.
|
|
|
|
|
.
|
\
|
|
|
|
|
|
.
|
\
|
|
|
|
|
|
.
|
\
|
|
|
|
|
|
.
|
\
|
1
0
2
0
,
5
3
2
1
,
0
1
1
2
,
3
2
1
3
3.
|
|
|
|
|
.
|
\
|
|
|
|
|
|
.
|
\
|
|
|
|
|
|
.
|
\
|
|
|
|
|
|
.
|
\
|
3
1
2
0
,
0
0
1
4
,
0
0
0
0
,
5
3
1
1
7. Hallar una base y la dimensin del espacio solucin de cada sistema homogneo:
a)
= + +
= +
= + +
0 8 5 3
0 5
0 2 3
z y x
z y x
z y x
b)
= +
= +
= + +
0 2 4 2 4 2
0 5 2 4 2
0 4 3 2
t s z y x
t s z y x
t s z y x
8. En R
n
un hiperplano que contiene a o es un subespacio de dimensin n 1. Si H es
un hiperplano en R
n
que contiene a o, demuestre que:
H = {(x
1
, x
2
,,x
n
): a
1
x
1
+ a
2
x
2
++ a
n
x
n
= 0} donde a
1
, a
2
,,a
n
son nmeros
reales , no todos ceros.
ESPACIOS VECTORIALES CON PRODUCTO INTERNO.
Sea V un espacio vectorial cualquiera, a cada par de vectores V v u e , se le asigna un
nmero real denominado producto interno o producto interior de v y u que se denota por
> < v u , que cumple las siguientes propiedades:
i. > < = > < u v v u , ,
ii. > < + > < = > + < w u v u w v u , , ,
iii. > < = > < v u k v u k , , para algn escalar k .
iv. 0 0 , 0 , = = > < > > < u u u y u u
Todo espacio vectorial que se define un producto interno, se denomina espacio con
producto interno.
Ejemplo. En R
2
y R
3
el producto interno conocido es el producto punto ya que cumple con
las cuatro propiedades anteriormente.
Ejemplo. Para los vectores ) , , ( ) , , (
3 2 1 3 2 1
v v v v y u u u u = = en R
3
puede definirse el
siguiente producto interno:
3 3 2 2 1 1
3 2 , v u v u v u v u + + = > < . Se deja al alumno que
demuestre que se cumplen las cuatro propiedades.
Tambin en el espacio de matrices, de polinomios y de funciones se pueden definir
productos interiores.
Sean
|
|
.
|
\
|
=
|
|
.
|
\
|
=
22 21
12 11
22 21
12 11
,
v v
v v
V
u u
u u
U , entonces:
22 22 21 21 12 12 11 11
, v u v u v u v u V U + + + = > <
es un producto interno para M
2x2
.
Si
2
2 1 0
2
2 1 0
, x b x b b q x a x a a p + + = + + = , un producto interno para el espacio de
polinomios de segundo grado es:
2 2 1 1 0 0
, b a b a b a q p + + = > < .
En el espacio de las funciones continuas en el intervalo | | b a, , el producto interno para dos
funciones en particular ) ( ), ( x g x f est dado por:
}
= > <
b
a
dx x g x f g f ) ( ) ( , .
El producto interior permite definir la norma de un vector, que de manera general est dada
por > < = u u u , . Esto significa que de acuerdo al producto interior que se utilice, la
norma va a variar. Esta norma no tiene ningn significado geomtrico excepto en el caso de
R
2
y R
3
cuando se considera como producto interior el producto punto o escalar de vectores
en el cual, esta norma se interpreta como el mdulo o tamao de un vector.
Si v y u son dos vectores cualesquiera de un espacio vectorial, se define la distancia entre
los vectores v y u como v u v u d = ) , ( . Un espacio que tiene definida una norma y
una distancia se denomina espacio mtrico y normado.
La norma tambin es utilizada para determinar el ngulo entre dos vectores, si v y u son
dos vectores cualesquiera de un espacio vectorial, el ngulo entre v y u
se determina
por:
v u
v u > <
=
,
cos
. Si el ngulo entre dos vectores es 90 grados, dichos vectores se
dice que son ortogonales.
Un vector unitario es un vector de norma uno. Se puede normalizar un vector no nulo
dividindolo entre su norma. En efecto:
u
u
.
Ejemplo. Encontrar el ngulo entre los vectores ) 3 , 2 , 1 , 2 ( ) 2 , 1 , 3 , 4 ( = = v y u .
Solucin.
El producto interno es 9 ) 3 )( 2 ( ) 2 )( 1 ( ) 1 )( 3 ( ) 2 )( 4 ( , = + + + = > < v u
Las normas de los vectores son: 18 30 = = v y u
As que:
0
78 . 112
18 30
9
cos =
=
BASES OROTONORMALES.
Se dice que un conjunto de vectores en un espacio de productos interiores es un conjunto
ortogonal si todas las parejas de vectores distintos en el conjunto son ortogonales. Un
conjunto ortogonal en el que cada vector tiene norma uno se conoce como ortonormal.
Ejemplo. El conjunto formado por los vectores )
2
1
, 0 ,
2
1
( ), 0 , 1 , 0 ( = = v u y
)
2
1
, 0 ,
2
1
( = w es ortonormal ya que cada uno de los vectores es unitario y son
ortogonales con el producto interno tradicional.
Una base ortonormal es un conjunto de vectores ortonormales que forman una base para un
espacio determinado.
Teorema. Si } , ... , , {
2 1 n
v v v S = es una base ortonormal para un espacio de productos
interiores V y si u es un vector cualquiera de V entonces:
n n
v v u v v u v v u u > < + + > < + > < = , ... , ,
2 2 1 1
. O sea, un vector se puede expresar
como combinacin lineal de los vectores de una base ortonormal, y los coeficientes de
dicha combinacin lineal est en trminos de productos interiores.
Teorema. Todo conjunto ortonormal de vectores es linealmente independiente.
Ejemplo. Dados los vectores )
5
4
, 0 ,
5
3
( ),
5
3
, 0 ,
5
4
( ), 0 , 1 , 0 (
3 2 1
= = = v v v , demostrar que
estos vectores forman una base ortonormal para R
3
y expresar ) 1 , 1 , 1 ( = w como
combinacin lineal de los vectores dados.
Solucin. Se puede observar que los tres vectores son unitarios, y adems los productos
internos de cada para de vectores distintos es cero. Por lo tanto como los vectores son
ortonormales, entonces, son linealmente independientes, adems como la cantidad de
vectores coincide con la dimensin del espacio, entonces, estos tres vectores forman una
base y esta base es ortonormal.
Luego,
5
7
)
5
4
, 0 ,
5
3
( ), 1 , 1 , 1 ( ,
5
1
)
5
3
, 0 ,
5
4
( ), 1 , 1 , 1 ( ,
1 ) 0 , 1 , 0 ( ), 1 , 1 , 1 ( ,
2
2
1
= > < = > <
= < = > <
= > < = > <
v u
v u
v u
As que:
2 2 1
5
7
5
1
v v v u + =
Proceso de Gram-Schmidt:
Todo espacio vectorial de productos interiores distinto del espacio nulo y de dimensin
finita tiene una base ortonormal.
Se puede tener una base inicial } , ... , , , {
3 2 1 n
u u u u B = y pasar por dicho proceso a otra base
que es ortonormal } , ... , , , {
3 2 1 n
v v v v B = con los siguientes pasos:
1. Se normaliza el primer vector de la base inicial para obtener
1
1
1
u
u
v =
2. Se encuentra un vector ortogonal al encontrado en el paso anterior y luego se
normaliza as:
1 1 2 2
1 1 2 2
2
,
,
v v u u
v v u u
v
> <
> <
=
3. Se encuentra un tercer vector ortogonal a los dos vectores del paso anterior y se
normaliza as:
2 2 3 1 1 3 3
2 2 3 1 1 3 3
2
, ,
, ,
v v u v v u u
v v u v v u u
v
> < > <
> < > <
=
El proceso contina de igual manera hasta llegar al vector n-simo.
Ejemplo. Dada la base de R
3
)} 0 , 0 , 1 ( ), 0 , 1 , 1 ( ), 1 , 1 , 1 ( {
1
= = u B . Ortonormalizar dicha base
usando el proceso de Gram Schmidt.
Solucin.
1. Se normaliza el primer vector )
3
1
,
3
1
,
3
1
(
1
= v
2. Se encuentra un vector ortogonal al anterior
)
3
1
,
3
1
,
3
1
( )
3
1
,
3
1
,
3
1
( ), 0 , 1 , 1 ( ) 0 , 1 , 1 (
2
> < = w
= )
3
2
,
3
1
,
3
1
( )
3
1
,
3
1
,
3
1
(
3
2
) 0 , 1 , 1 ( =
)
6
2
,
6
1
,
6
1
(
9
4
9
1
9
1
)
3
2
,
3
1
,
3
1
(
2
=
+ +
= v
3. Se encuentra un vector ortogonal a los dos anteriores.

)
6
2
,
6
1
,
6
1
( )
6
2
,
6
1
,
6
1
( ), 0 , 0 , 1 ( )
3
1
,
3
1
,
3
1
( )
3
1
,
3
1
,
3
1
( ), 0 , 0 , 1 ( ) 0 , 0 , 1 (
3
> < > < = w
) 0 ,
2
1
,
2
1
( )
3
1
,
6
1
,
6
1
( )
3
1
,
3
1
,
3
1
( ) 0 , 0 , 1 (
3
= = w
Y normalizando este resultado obtenemos: ) 0 ,
2
1
,
2
1
(
0
4
1
4
1
) 0 ,
2
1
,
2
1
(
3
=
+ +
= v
As pues, la base ortonormal es } ) 0 ,
2
1
,
2
1
( ),
6
2
,
6
1
,
6
1
( ),
3
1
,
3
1
,
3
1
( { = B
CAMBIO DE BASE.
Todo punto en un sistema de coordenadas puede representarse como combinacin lineal de
los vectores de una base. As, dadas dos bases } , { } , {
2 1 2 1
v v B y u u B = = se desea pasar la
combinacin lineal de la primera a la combinacin lineal en la segunda base.
Sea } ..., , , {
2 1 n
v v v B= una base cualquiera de un espacio vectorial, entonces, todo vector u
de dicho espacio puede expresarse como
n n
v c v c v c u + + + = ...
2 2 1 1
, entonces, los
escalares
n
c c c , ... , ,
2 1
se denominan coordenadas relativas de u respecto a la base B . El
vector de coordenadas para u en dicha base es ) , ... , , ( ) (
2 1 n B
c c c u = y la matriz de
coordenadas de u respecto a la base B est dada por: | |
(
(
(
(
(
(
=
n
B
c
c
c
u
.
.
2
1
Veamos para R
2
como se hara el cambio de una base } , {
2 1
u u B= a otra base } , { '
2 1
v v B = .
Expresamos los vectores de la base inicial como combinacin lineal de los vectores de la
base final:
2 1 2 2 1 1
, v d v c u v b v a u + = + = . Sea w
2
R we con matriz de coordenadas
respecto a la base inicial | |
(
=
2
1
k
k
w
B
. De esta forma se tiene que:
2 2 1 1 2 1 2 1 2 2 1 1 2 2 1 1
) ( ) ( ) ( ) ( v d k b k v c k a k v d v c k v b v a k u k u k w + + + = + + + = + =
As la matriz de coordenadas de w con respecto a la base ' B est dada por:
| | | |
B B
w P
k
k
d b
c a
d k b k
c k a k
w =
(
=
(
+
+
=
2
1
2 1
2 1
'
A la matriz
(
=
d b
c a
P se le denomina matriz de transicin de B hacia B.
En general, la matriz de transicin se construye usando como columnas las matrices de
coordenadas de los vectores de la base inicial con respecto a la base final.
Observe que: | | | |
(
=
(
=
d
c
u y
b
a
u
B B ' 2 ' 1
Esta matriz de transicin es una matriz no singular, o sea, que posee inversa
1
P y esta
inversa es la matriz de transicin de Bhacia B.
Si las bases B y B son bases ortonormales la matriz de transicin P es una matriz
ortogonal, es decir,
T
P P =
1
.
Ejemplo. Sea B = {(1,0), (0,1)} y B = { (1,1), (2,1)}. a) Hallar la matriz de transicin de B
hacia B , b) Hallar | | ) 2 , 7 (
'
= w si w
B
.
Solucin.
a) Expresamos primero los vectores de la base inicial como combinacin lineal de los
vectores de la base final. De esta manera:
) 1 , 2 ( ) 1 , 1 ( ) 0 , 1 (
2 1
c c + = , de donde se obtiene que 1 1
2 1
= = c y c
) 1 , 2 ( ) 1 , 1 ( ) 1 , 0 (
2 1
k k + = , de lo que resulta 1 2
2 1
= = k y k
Ahora encontramos las matrices de coordenadas de cada uno de estos vectores en
trminos de la base B:
| |
(
=
1
1
) 0 , 1 (
' B
y | |
(
=
1
2
) 1 , 0 (
' B
y
(
=
1 1
2 1
P
b) | |
(
=
2
7
B
w , en este caso, la matriz de coordenadas coincide con las componentes del
vector por que la base inicial B es la base cannica..De esta manera:
| |
(
=
(
=
5
3
2
7
1 1
2 1
' B
v y la combinacin lineal en trminos de la base B es:
) 1 , 2 ( 5 ) 1 , 1 ( 3 + = v
1. Con el producto interno
2 2 1 1
3 2 , v u v u v u + = > < donde ) , ( ) , (
2 1 2 1
v v v y u u u = = ,
calcular dicho producto para cada par de vectores dados:
a) (2, 1) , (-1, 3) b) (0,0), (7,2) c) (3,1), (-2,9)
2. Sean ) , , ( ) , , (
3 2 1 3 2 1
v v v v y u u u u = = determine cuales de las siguientes expresiones
son productos interiores para R
3
:
a)
3 3 1 1
, v u v u v u + = > <
b)
2
3
2
3
2
2
2
2
2
1
2
1
, v u v u v u v u + + = > <
c)
3 3 2 2 1 1
4 2 , v u v u v u v u + + = > <
3.
|
|
.
|
\
|
=
|
|
.
|
\
|
=
h g
f e
V y
d c
b a
U Sean . Determinar si dh cf bg ae V U + + + = > < , es un
producto interior sobre el espacio M
2x2
. Si no lo es, indicar que propiedad o propiedades de
producto interno no cumple.
4. Suponga el producto interno en R
3
definido como
3 3 2 2 1 1
3 2 , v u v u v u v u + + = > < .
Use dicho producto para determinar en cada caso el valor de k para que los vectores
dados sean ortogonales.
a) (2, 1, 3) y (1, 7, k) b) (k, k, 1) y (k, 5, 6)
5. Con el producto interior en R
3
(producto escalar) , use el proceso de Gram-Schmidt
para transformar las bases dadas en una base ortonormal:
a) (1, 1, 1), (-1, 1, 0), (1, 2, 1)
b) (1, 0, 0), (3, 7, -2), (0, 4, 1)
6. Repita el procedimiento del ejercicio anterior usando el producto interior del ejercicio
4.
7. Con el producto escalar tradicional en R
4
, ortonormalizar la base dada por los vectores
(0, 2, 1,0), (1, -1, 0, 0), (1, 2, 0, -1), (1, 0, 0, 1).
8. Considere las bases B = {(1,0), (0,1)} y B = { (2,1), (-3,4)} :
a) Hallar la matriz de transicin de B a B
b) Calcular la matriz de coordenadas | |
' B
w siendo ) 5 , 3 ( = w
c) Hallar la matriz de transicin de B a B
9. Repita el ejercicio 8 con B = { (-3, 0, -3), (-3,2,-1), (1,6,-1)} y B = {(-6,-6,0), (2,-6,4),
(-2,-3, 7)} y ) 5 , 8 , 5 ( = w .
10. Repita las instrucciones del ejercicio 8 con B = {6 + 3x, 10+2x} y B={2, 3+2x} y w =
-4 + x
11. Dado el conjunto de vectores {(0, 3/5, 4/5), (-1, 0, 0), (0, -4/5, 3/5)} demostrar que
estos vectores forman una base ortonormal y expresar los vectores (1, 1, 1), (2, 5, -7)
como combinacin lineal de los vectores del conjunto haciendo uso de producto
interno.
12. Construya una base ortonormal para el espacio o subespacio vectorial dado
a) t = {(x, y, z): 2x y z = 0}
b) t = {(x, y, z): 3x 2y + 6z = 0}
c) t = {(x, y, z):
4 3 2
z y x
= = }
d) t = {(x, y, z): ax + by + cz = 0}
e) H es el espacio de soluciones de :
|
|
|
.
|
\
|
= +
= +
= +
0 5 8 4
0 3 2 2
0 3
z y x
z y x
z y x

13. Encuentre Proy
H
V
a) {
2
R
y
x
e
|
|
.
|
\
|
: ax + by = 0} v =
|
|
.
|
\
|
b
a
{
3
R
z
y
x
e
|
|
|
.
|
\
|
: ax + by + cz = 0} v =
|
|
|
.
|
\
|
c
b
a

b) {
3
R
z
y
x
e
|
|
|
.
|
\
|
: 3x 2y + 6z = 0} v =
|
|
|
.
|
\
|
4
1
3
c) {
4
R
w
z
y
x
e
|
|
|
|
|
.
|
\
|
: 2x y + 3z w = 0} v =
|
|
|
|
|
.
|
\
|
3
2
1
1
d) {
4
R
w
z
y
x
e
|
|
|
|
|
.
|
\
|
: x = 3y . w = 3y} v =
|
|
|
|
|
.
|
\
|
1
3
2
1
14. En los ejercicios siguientes exprese x en trminos de B
2
.
a) Sea (x)
B1
=
|
|
.
|
\
|
1
2
; Sea B
1
=
)
`
|
|
.
|
\
|
|
|
.
|
\
|
1
2
,
4
5
y B
2
=
)
`
|
|
.
|
\
|
|
|
.
|
\
|
1
0
,
0
1
b) Sea (x)
B1
=
|
|
.
|
\
|
1
2
; Sea B
1
=
)
`
|
|
.
|
\
|
|
|
.
|
\
|
1
1
,
2
3
y B
2
=
)
`
|
|
.
|
\
|
|
|
.
|
\
|
1
2
,
1
3
c) Sea (x)
B1
=
|
|
.
|
\
|
2
3
; Sea B
1
=
)
`
|
|
.
|
\
|
|
|
.
|
\
|
0
24
,
6
12
y B
2
=
)
`
|
|
.
|
\
|
|
|
.
|
\
|
0
6
,
0
6
d) Sea (x)
B1
=
|
|
|
.
|
\
|
1
2
4
; Sea B
1
=
|
|
|
.
|
\
|
|
|
|
.
|
\
|
|
|
|
.
|
\
|
50
22
10
,
14
2
6
,
10
2
2
y B
2
=
|
|
|
.
|
\
|
|
|
|
.
|
\
|
|
|
|
.
|
\
|
0
4
0
,
2
2
2
,
10
2
2
e) Sea (x)
B1
=
|
|
|
.
|
\
|
3
5
7
; Sea B
1
=
|
|
|
.
|
\
|
|
|
|
.
|
\
|
|
|
|
.
|
\
|
46
51
25
,
23
21
13
,
10
6
8
y B
2
=
|
|
|
.
|
\
|
|
|
|
.
|
\
|
|
|
|
.
|
\
|
0
3
0
,
1
3
1
,
11
9
7
f) Sea (x)
B1
=
|
|
|
.
|
\
|
4
2
5
; Sea B
1
=
|
|
|
.
|
\
|
|
|
|
.
|
\
|
|
|
|
.
|
\
|
0
0
26
,
2
9
48
,
1
5
7
y B
2
=
|
|
|
.
|
\
|
|
|
|
.
|
\
|
|
|
|
.
|
\
|
0
3
2
,
0
1
8
,
1
5
7
TRANSFORMACIONES LINEALES.
Sean W y V dos espacios vectoriales y T una funcin que asocia un vector nico en
W con cada vector en V , se dice que T aplica W en V . Es decir, a cada vector V v e se le
asocia como imagen bajo T un vector W w e .
Ejemplo. Sea T: R
2
R
3
dada por T(x,y) = (x, x + y, x y). En este caso un vector del
espacio R
2
se transforma mediante T a un vector en R
3
. As, T(1,1) = (1, 1+1, 1-1) = (1, 2,
0).
Una transformacin W V T : es una transformacin lineal si para cada V v u e , se
cumple que:
i. ) ( ) ( ) ( v T u T v u T + = +
ii. ) ( ) ( u T k u k T = para algn escalar k
Ejemplo. Sea T: R
2
R
3
dada por T(x,y) = (x, x + y, x y). Determinar si T es o no es
lineal.
Sean , ,
2
R v u e entonces, ) , ( ), , ( ), , (
2 2 1 1 2 1 2 1
v u v u v u v v v u u u + + = + = = , de esta
forma:
i. ) , , ( ) , ( ) (
2 2 1 1 2 2 1 1 1 1 2 2 1 1
v u v u v u v u v u v u v u T v u T + + + + + = + + = +
= ) ( ) ( ) , , ( ) , , (
2 1 2 1 1 2 1 2 1 1
v T u T v v v v v u u u u u + = + + +
ii. ) ( ) , , ( ) , , ( ) , ( ) (
2 1 2 1 1 2 1 2 1 1 2 1
u T k u u u u u k ku ku ku ku ku ku ku T u k T = + = + = =
Por lo tanto, se cumplen las dos condiciones, y T es lineal.
Sea W V T : una transformacin lineal, entonces, para V v v e
2 1
, y para escalares
2 1
k y k se cumple que ) ( ) ( ) (
2 2 1 1 2 2 1 1
v T k v T k v k v k T + = + .
De igual forma, si
n
v v v ..., , ,
2 1
son vectores en V y si
n
k k k , ... , ,
2 1
son escalares y la
transformacin W V T : es lineal, entonces:
) ( ... ) ( ) ( ) ... (
2 2 1 1 2 2 1 1 n n n n
v T k v T k v T k v k v k v k T + + + = + + + .
Ejemplos de algunas transformaciones lineales:
1.
m n
R R T : dado por x A x T = ) ( donde A es una matriz de orden m x n.
2. La transformacin cero, W V T : donde V v v T e = , 0 ) ( .
3. La transformacin identidad, V V T : con V v v v T e = ) ( .
4. Dilatacin o contraccin de un vector, V V T : con V v v k v T e = ) ( y algn
escalar k .
5. La transformacin derivada y la transformacin integral en el espacio de funciones son
transformaciones lineales. O sea:
F F T : dada por ) ( f f T = y
}
= dx x f F I con F F I ) ( ) ( :
son transformaciones lineales segn las propiedades de la derivada y de la integral.
Teorema. Sea W V T : una transformacin lineal, entonces:
i. 0 ) 0 ( = T
ii. ) ( ) ( v T v T =
iii. ) ( ) ( ) ( w T v T w v T =
Demostracin (ii).
Sea V v e y sea W V T : una transformacin lineal, entonces:
) ( ) ( ) 1 ( ) ) 1 ( ( ) ( v T v T v T v T = = =
Se deja la demostracin (i) y (iii) al estudiante.
NCLEO Y RECORRIDO DE UNA TRANSFORMACIN LINEAL.
Si W V T : es una transformacin lineal, entonces, el conjunto de vectores en V que
aplica hacia W e 0 se conoce como ncleo o Kernel o espacio nulo de T y se denota por
Ker(T). El conjunto de todos los vectores en W que son imgenes bajo T de al menos un
vector en V se conoce como recorrido de T y se denota por R(T).
Ejemplo. En el caso de la transformacin cero W V T : , V T Ker = ) ( puesto que todos
los vectores aplican hacia el cero y } 0 { ) ( = T R puesto que es el nico elemento al cual
llegan todos los vectores de V .
Ejemplo. Sea
m n
R R T : la transformacin que multiplica
(
(
(
(
n
x
x
x
.
2
1
por la matriz
(
(
(
=
nn n n
n
a a a
a a a
A
...
...
2 1
1 12 11
. El ncleo de esta transformacin consiste en todos los vectores x
que son solucin del sistema homogneo 0 = x A , o sea:
= + + +
= + + +
= + + +
0 ...
0 ...
0 ...
2 2 1 1
2 2 22 1 21
1 2 12 1 11
n nn n n
n n
n n
x a x a x a
x a x a x a
x a x a x a
El recorrido de T consiste de todos los vectores
(
(
(
(
=
n
b
b
b
b
.
2
1
tal que el sistema b x A = es un
sistema compatible.
Ejemplo. Sea
2 4
: R R T dada por ) , ( ) , , , ( c b b a d c b a T + + = .Hallar el ncleo y
recorrido de la transformacin.
Solucin. El ncleo es el conjunto de vectores de R
4
que aplican al cero en R
2
, de esta
forma se tiene que:
} , ) , , , ( { } , ) , , , ( { } 0 , 0 ) , , , ( { ) ( R d a d a a a c b a b d c b a c b b a d c b a T Ker e = = = = = + = + =
El recorrido consiste de aquellos vectores en R
2
tal que c b y b a x + = + = ,
} , , ) , ( { ) ( R c b a c b b a T R e + + =
Teorema. Sea W V T : una transformacin lineal, entonces:
i. ) (T Ker es un subespacio de V
ii. ) (T R es un subespacio de W
Demostracin.
Sean ) ( ,
2 1
T Ker v v e , entonces, 0 0 0 ) ( ) ( ) (
2 1 2 1
= + = + = + v T v T v v T , de esta forma,
se cumple con la propiedad de cerradura con respecto a la suma, o sea,
) ( ) (
2 1
T Ker v v e + .
Adems, sea k un escalar, entonces, 0 0 . ) ( ) (
1 1
= = = k v T k v k T , por lo tanto, se cumple
la cerradura respecto al producto escalar-vector, o sea, ) ( 1 T Ker v k e
.
As, ) (T Ker es un subespacio de V .
Se deja al estudiante la demostracin del inciso (ii).
Supongamos que un conjunto de vectores } , ... , , {
2 1 n
v v v es una base para un espacio
vectorial V y W V T : una transformacin lineal . Si se conocen las imgenes
) ( , ... ), ( ), (
2 1

n
v T v T v T , entonces, se puede obtener la imagen de
v expresando previamente
v como combinacin lineal de los vectores de la base, es decir,

n n
v k v k v k v + + + = ...
2 2 1 1
y luego ) ( ... ) ( ) ( ) (
2 2 1 1 n n
v T k v T k v T k v T + + + = . O sea, una
transformacin lineal est completamente determinada por sus valores en una base.
Ejemplo. Sea la base de R
3
{(1, 1, 1), (1, 1, 0), (1, 0, 0)} con T(1, 1,1) = (1, 0), T(1, 1, 0) =
(2, -1) y T(1, 0, 0) = (4, 3). Determinar T(2, -3, 5).
Solucin.
Primeramente se expresa (2, -3, 5) como combinacin lineal de los vectores de la base. De
esta forma se tiene que (2, -3, 5) = 5(1, 1,1)- 8(1, 1, 0) + 5(1, 0, 0). Aplicando la propiedad
antes mencionada, se obtiene:
T(2, -3, 5) = 5 T(1, 1, 1) 8 T(1, 1,0) + 5 T(1, 0, 0) = 5 (1, 0) 8 (2, -1) + 5 (4, 3)
= ( 9, 23).
Si W V T : es una transformacin lineal, la dimensin del recorrido de T se conoce
como rango de T y la dimensin del ncleo se denomina nulidad de T. Adems, si
n V = dim entonces, se tiene que: (rango T) + (nulidad de T) = n.
1. Para cada funcin F : R
2
R
2
, determinar si F es lineal: a) F(x, y) = (2x, y) b) F(x,
y) = (x, y+1) c) F(x, y) = (y, y)
2. Repetir el ejercicio 1 para cada funcin F: R
3
R
2
: a) F(x, y, z) = (x, x + y + z) b)
F(x, y, z) = (1, 1) c) F(x, y, z) = (0, 0)
3. Determine si H: P
2
P
2
es lineal:
a) H(a
0
+ a
1
x + a
2
x
2
) = a
0
+ (a
1
+ a
2
) x + (2 a
0
- 3 a
1
)x
2
b) H(a
0
+ a
1
x + a
2
x
2
) = a
0
+ a
1
(x +1)+ a
2
(x + 1)
2
c) H(a
0
+ a
1
x + a
2
x
2
) = (a
0
+ 1) + a
1
x + a
2
x
2

4. Determine si G es lineal con G: M
2 x 2
R :
a) d a
d c
b a
G + =
|
|
.
|
\
|
(
b)
(
=
|
|
.
|
\
|
(
d c
b a
d c
b a
G det
c)
2 2
d a
d c
b a
G + =
|
|
.
|
\
|
(
d) d c b a
d c
b a
G + + =
|
|
.
|
\
|
(
3 2
5. Sea B una matriz fija de orden 2 x 3. Demuestre que la funcin T: M
2x2
M
2x3
definida por T(A) = A B es una transformacin lineal.
6. Sea } , ... , , {
2 1 n
v v v una base para un espacio vectorial V y supngase que W V T : es
una transformacin lineal. Demuestre que si 0 ) ( ... ) ( ) (
2 1
= = = =
n
v T v T v T , entonces, T
es la transformacin cero.
7. Sea } , ... , , {
2 1 n
v v v una base para un espacio vectorial V y supngase que V V T : es
un operador lineal. Demuestre que si
1 1
) ( v v T = ,
2 2
) ( v v T = , ...,
n n
v v T = ) ( , entonces,
T es la transformacin identidad sobre V.
8. Sea T: R
2
R
2
la multiplicacin por
(

4 8
1 2
i. Cules de las siguientes matrices estn en el recorrido de T:
(
4
1

(
0
5

(
12
3
ii. Cules de las siguientes matrices estn en ) (T Ker ?
(
10
5

(
2
3

(
1
1
9. Repetir el ejercicio 8 ahora con
3 4
: R R T y
|
|
|
.
|
\
|

9 9 0 6
4 1 1 2
3 2 1 4
i)
(
(
(
6
0
0

(
(
(
(
(
(
1
4
2
0
3
1
ii)
(
(
(
(
(
(
(
(
(
(
(
(
0
1
4
0
1
0
0
0
0
2
8
3
10. Igual que 8 con T : P
2
P
2
y T(p(x)) = x p(x):
i) x + x
2
, 1 + x , 3 x
2
ii) x
2
, 0 , 1 + x
11.Sea V cualquier espacio vectorial y supngase que T : V V est definida por
v v T 3 ) ( = . Cul es el ncleo de T? Cul es el recorrido de T?
MATRIZ ASOCIADA A UNA TRANSFORMACIN LINEAL. MATRICES
SEMEJANTES.
Sea W V T : una transformacin lineal y sean B y B bases para W y V
respectivamente. Adems se conoce que m W y n V = = dim dim , entonces, para cada
V x e la matriz de coordenadas | |
B
x es un vector de R
n
y la matriz de coordenadas
| |
'
) (
B
x T es un vector de R
m
. Se desea encontrar una matriz
n x m
A tal que
| | | |
'
) (
B B
x T x A = .
Sean } , ... , , { ' } , ... , , {
2 1 2 1 m n
v v v B y u u u B = = .
Si
(
(
(
(
(
=
mn m m
n
n
a a a
a a a
a a a
A
...
...
...
2 1
2 22 21
1 12 11
, entonces, sucede que:
| | | |
' 1
21
11
1
) (
B
mn
b
u T
a
a
a
u A =
(
(
(
(
=
De igual forma
| |
(
(
(
(
(
=
nj
j
j
B
j
a
a
a
u A
2
1
y as | | | | | | | |
n x m B n B B
u T u T u T A
' ' 2 ' 1
) ( ... ) ( ) ( =
Ejemplo. Sea
1 2
: P P T la transformacin lineal definida por ) ( )) ( ( x p x x p T = .
Encontrar la matriz asociada a T con respecto a las bases B ={1, x} y B = {1, x, x
2
}.
Solucin. Primeramente se encuentran las transformaciones de los vectores de la base
inicial, as, T(1) = x.1 = x y T(x) = x. x = x
2
. Luego se expresan los vectores
transformados de la base inicial como combinacin lineal de los vectores de la base final y
as T(1) = x = 0(1) + 1(x) + 0(x
2
) y T(x) = x
2
= 0(1) + 0(1) +1(x
2
)
De esta forma se tiene que:
| | | |
(
(
(
=
(
(
(
=
(
(
(
=
1 0
0 1
0 0
1
0
0
) (
0
1
0
) 1 (
' '
A as y x T y T
B B
La matriz asociada a una Transformacin lineal se puede utilizar para encontrar la
transformacin de cualquier vector del espacio vectorial de partida. Por ejemplo,
2
2 ) 2 1 ( ) 2 1 ( x x x x x T = = . Haciendo uso de la matriz asociada obtenemos que:
i. | |
(
=
2
1
2 1
B
x
ii. | | | |
B B
v A v T =
'
) ( . Por lo tanto, se tiene que | |
(
(
(
=
(
(
(
(
=
2
1
0
2
1
1 0
0 1
0 0
) 2 1 (
' B
x T
iii.
2 2
2 ) ( 2 ) ( 1 ) 1 ( 0 ) 2 1 ( x x x x x T = + =
Si la transformacin lineal est en el mismo espacio, es decir, V V T : entonces, se
puede tomar B = B y la matriz resultante se conoce como matriz de T con respecto a la
base B . Si la dimensin del espacio es n, entonces, la matriz obtenida es una matriz
cuadrada de orden n.
Ejemplo 1. Si } , ... , , {
2 1 n
u u u B = es cualquier base para un espacio vectorial V de
dimensin finita y si V V I : es el operador identidad sobre V , entonces, se cumple que
n n
u u I u u I u u I = = = ) ( , ... , ) ( , ) (
2 2 1 1
y de esta forma los vectores asociados son los
vectores cannicos, y la matriz asociada es la matriz identidad
n
I .
Ejemplo 2. Sea
2 2
: R R T el operador lineal definido como
(
+
+
=
(
y x
y x
y
x
T
4 2
.
Encontrar la matriz asociada a T con respecto a la base }
2
1
,
1
1
{
(
= B .
Solucin.
) 2 , 1 ( 3 ) 6 , 3 ( ) 2 , 1 ( ) 1 , 1 ( 2 ) 2 , 2 ( ) 1 , 1 ( = = = = T y T .De esta forma, la matriz asociada a T est
dada por
(
=
3 0
0 2
A .
Teorema. Sea V V T : una transformacin lineal sobre un espacio vectorial de
dimensin finita. Si A es la matriz de transicin de T con respecto a una base B y A es la
matriz de T con respecto a una base B entonces , P A P A
1
'

= donde P es la matriz de
transicin de B hacia B.
Ejemplo. En el ejercicio anterior, sea B = {(1, 0), (0, 1)} y B= {(1, 1), (1,2)}, entonces,
(
=
3 0
0 2
' A . Ahora bien, T(1,0) = (1, -2) y T(0, 1) = (1,4). As,
(
=
4 2
1 1
A .
La matriz de transicin de B hacia B es
(
=
2 1
1 1
P . Puede demostrarse que :
(
=
(

= =

3 0
0 2
2 1
1 1
4 2
1 1
2 1
1 2
'
1
P A P A .
Si A y B son dos matrices cuadradas, se dice que A es semejante a B si existe una matriz
inversible P tal que P A P B
1
= . En el ejemplo anterior, las matrices A y A son
semejantes. Adems, puede demostrarse que si B es semejante a A, entonces, tambin, A es
semejante a B. (Se deja esta ltima demostracin al estudiante).
VALORES Y VECTORES PROPIOS.
Si A es una matriz cuadrada de orden n, entonces, se dice que un vector diferente de cero
n
R x e es un vector propio (o eigenvector o vector caracterstico) de la matriz A si
x x A = para algn escalar . El valor se denomina valor propio ( o eigenvalor o
valor caracterstico) de A y se dice que x es un vector propio correspondiente al valor
propio .
Ejemplo. El vector
(
=
2
1
x es un eigenvector para la matriz
(
=
1 8
0 3
A correspondiente
al eigenvalor = 3 porque:
x x A 3
6
3
2
1
1 8
0 3
=
(
=
(
= .
Para encontrar los eigenvalores de una matriz A escribimos:
0 ) ( = = = x I A x I x A x x A .
Para que sea un eigenvalor debe haber una solucin distinta de la trivial de esta
ecuacin, o sea, 0 ) ( det = I A .
Esta ecuacin se conoce como ecuacin caracterstica de A, los escalares que satisfacen
esta ecuacin son los eigenvalores de A. Cuando se desarrolla este determinante nos queda
un polinomio en de grado n conocido como polinomio caracterstico de A.
Ejemplo. Hallar los valores y vectores propios de la matriz
(
=
0 1
2 3
A .
Solucin.
Planteamos inicialmente la ecuacin caracterstica:
2 , 1 0 ) 1 )( 2 ( 0 2 3 0
1
2 3
) det(
2
= = = + + =
I A
Para encontrar los vectores propios sustituimos los valores propios en la ecuacin
0 ) ( = x I A .
Si = 1, se obtiene el sistema de ecuaciones:
2 1
2 1
2 1
2
1
0
0 2 2
0
0
1 1
2 2
x x
x x
x x
x
x
=
=
=
=
(
Esto significa que

(
=
(
=
1
1
2
2
2
x
x
x
x . O sea, que los vectores propios correspondientes al
valor propio =1, son mltiplos escalares o combinacin lineal del vector
(
1
1
.
Para
2 1
2 1
2 1
2
1
2
0 2
0 2
0
0
2 1
2 1
; 2 y y
y y
y y
y
y
=
=
=
=
(
=
Por lo tanto, se tiene que
(
=
(
=
1
2 2
2
2
2
y
y
y
y . Esto es, todo vector propio correspondiente a
= 2, es combinacin lineal del vector
(
1
2
.
Los eigenvalores correspondientes al eigenvalor son vectores no nulos del espacio de
soluciones de 0 ) ( = x I A . A este espacio de soluciones se le conoce como eigenespacio
(o espacio propio o espacio caracterstico) de A correspondiente a . Los valores y
vectores propios se pueden tanto para operadores lineales como para matrices. Si T es una
transformacin lineal en un espacio vectorial V y A es la matriz asociada a T con respecto a
una base B dada, los valores y vectores propios correspondientes a la matriz A son los
mismos valores y vectores propios correspondientes a la transformacin lineal T definida
inicialmente.
Ejemplo. Hallar los eigenvalores y bases para los eigenespacios del operador lineal
2 2
: P P T definido por
2 2
) 5 ( ) 3 2 ( ) 2 3 ( ) ( x c x b a b a c bx ax T + + + = + + con la base
} , , 1 {
2
x x B= .
Solucin. .Primero debe encontrarse la matriz correspondiente a la base dada. Dicha matriz
es la siguiente:
(
(
(

=
5 0 0
0 3 2
0 2 3
A
La ecuacin caracterstica est dada por 0
5 0 0
0 3 2
0 2 3
=
O sea: 1 ; 5 0
3 2
2 3
5
3 2 1
= = = =

.
Si = 5, se tiene el siguiente sistema de ecuaciones:
libre iable x x x
x x
x x
x
x
x
var
0 2 2
0 2 2
0
0
0
0 0 0
0 2 2
0 2 2
3 2 1
2 1
2 1
3
2
1
= A =
=
=
(
(
(
=
(
(
(
(
(
(

De esta forma, un valor propio para el valor propio = 5 est dado por el vector:
(
(
(
+
(
(
(
=
(
(
(
=
1
0
0
0
1
1
3 2
3
2
2
x x
x
x
x
X . O sea, X es combinacin lineal de los vectores (-1, 1, 0) y
(0, 0, 1). Esto implica que esos vectores forman la base para el espacio propio formado por
el valor propio = 5.
Si = 1, el sistema formado est dado por:
0 ,
0 4
0 2 2
0 2 2
0
0
0
4 0 0
0 2 2
0 2 2
3 2 1
3
2 1
2 1
3
2
1
= =
=
= +
=
(
(
(
=
(
(
(
(
(
(

y y y
y
y y
y y
y
y
y
As, el vector propio asociado al valor propio = 1 es:
(
(
(
=
(
(
(
=
0
1
1
0
2 2
2
y y
y
Y . Entonces, la base para el espacio propio correspondiente al valor propio
= 1 est compuesta por el vector (1,1,0).

1. Sea
1 2
: P P T la transformacin lineal dada por
) 3 2 ( ) ( ) (
2 1 1 0
2
2 1 0
x a a a a x a x a a T + + + = + + , halle la matriz de T con respecto a las
bases estndar para P
2
y P
1.
2. Sea
3 2
: R R T dada por ) 0 , , 2 ( ) , ( x y x y x T + = . Hallar la matriz asociada a T
con respecto a las bases B = { (1, 3), (-2, 4)} y B = {(1,1,1), (2, 2,0), (3, 0, 0)}.
3. Sea )} 4 , 1 ( ), 3 , 1 ( {
2 1
= = = v v B y suponga
(
=
5 2
3 1
A la matriz de la
transformacin en R
2
con respecto a la base B:
a) Hallar | | | |
B B
v T y v T ) ( ) (
2 1
b) Encuentre ) ( ) (
2 1
v T y v T
c) Halle T(1, 1).
4. Sea
4 2
: P P T la transformacin lineal definida por ) ( )) ( (
2
x p x x p T = :
a) Halle la matriz de T con respecto a las bases B = {1 + x
2
, 1+ 2x + 3x
2
, 4 +
5x + x
2
} y B la base estndar de P
2
.
b) Use la matriz obtenida en (a) para calcular T(-3 + 5x 2x
2
).
5. Sea
(
(
(
=
4 2 6
5 0 2
1 3 1
A la matriz de
2 2
: P P T con respecto a la base B = { 3x + 3x
2
,
-1 + 3x + 2x
2
, 3 + 7x + 2x
2
}.
a) Hallar | | | | | |
B B B
x x T x x T x x T ) 2 7 3 ( , ) 2 3 1 ( , ) 3 3 (
2 2 2
+ + + + +
b) Encuentre T(3x+ 3x
2
), T(1 + 3x + 2x
2
), T(3 + 7x + 2x
2
)
c) Halle T(1 + x
2
)
6. Demuestre que si W V T : es la transformacin cero, entonces, la matriz de T con
respecto a cualquier base para W y V es una matriz cero.
7. Sea
2 2
: P P D el operador de derivacin D(p) = p . En los incisos (a) y (b) halle
la matriz de D con respecto a las base B = { p, q, r } :
a) p = 1, q = x, r = x
2
b) p = 2, q = 2 2x, r = 2 3x +8x
2
c) Use la matriz que encontr en (a) para calcular D(6 6x +24x
2
)
d) Repita el inciso ( c ) usando la matriz hallada en (b)
8. Halle la matriz A con respecto a B, calcular la matriz A de T con respecto a B
usando A = P
1
A P donde P es la matriz de transicin de B a B:
a)
2 2
: R R T con T(x, y) = (x 2y, -y) con B = { (1, 0), (0, 1) } y B = {(2, 1), (-3,
4) }
b)
3 3
: R R T con T(x, y, z) = (x + 2y z, -y, x + 7z) con B = {(1,0,0), (0, 1, 0), (0,
0, 1)} y B = { (1, 0, 0), (1, 1, 0), (1, 1, 1)}
c)
1 1
: P P T con T(a + bx) = a + b(x+1) con B = { 6+ 3x, 10 + 2x} y B = { 2, 3 +
2x}
9. Probar que si A y B son matrices semejantes entonces, det(A) = det(B) .
10. Probar que si A y B son matrices semejantes, entonces, A
2
y B
2
son semejantes, y
de modo ms general A
k
y B
k
son tambin semejantes donde k es un entero positivo.
11. Para cada matriz dada, encontrar la ecuacin caracterstica, los eigenvalores y las
bases para los eigenespacios correspondientes.
a)
(
1 8
0 3
b)
(
2 4
9 10
c)
(
(
(
1 0 2
0 1 2
1 0 4
d)
(
(
(
(
2 1 1
0 1
5
1
5 0 3
12. .Sea
2 2
: P P T dado por T(a + bx + cx
2
) = (5a + 6b + 2c) ( b + 8c)x + (a
2c)x
2
. Hallar los eigenvalores de T y las bases para los eigenespacios de T.
13. Encuentre la matriz asociada a la transformacin lineal dada.
a) T: R
2
R
2
; T
|
|
.
|
\
| +
=
|
|
.
|
\
|
y
y x
y
x
b) T: R
2
R
3
; T
|
|
|
.
|
\
|
+
=
|
|
.
|
\
|
y x
y
y x
y
x
2
c) T: R
3
R
2
; T
|
|
.
|
\
|
+
+
=
|
|
|
.
|
\
|
z y
y x
z
y
x
d) T: R
3
R
3
; T
|
|
|
.
|
\
|
+
+
=
|
|
|
.
|
\
|
z
z y
z y x
z
y
x
4 2
14. Determine Ker (T) y Nul (T).
a) T : R
2
R
3
; T (x, y) = (x + y, 3x, 2y)
b) T : R
2
R
2
; T (x, y) = (5x y, x + 2y)
c) T : R
5
R
3
; T(x, y, z, u, w) = (x- y + 6w, z + 5u w, x - y + 4w + 2z + 10u)
d) T:R
2
R
4
; T (x, y) = (2x + 3y, x y, 2x, 5x 4y)
e) T: R
3
R
2
; T(x, y, z) = (2x y 2z, x + 6y z)
15. En los siguientes ejercicios encuentre A
T
, Ker(T), Img(T), Rng(T), Nul(T).
a) T: R
2
R
3
; T
|
|
|
.
|
\
|
+
+
=
|
|
.
|
\
|
y x
y x
y x
y
x
3 2
b) T: R
3
R
3
; T
|
|
|
.
|
\
|
+
+ +
+
=
|
|
|
.
|
\
|
z y x
z y x
z y x
z
y
x
8 5
4 3
2
c) T: R
3
R
3
; T
|
|
|
.
|
\
|
+ +

+ +
=
|
|
|
.
|
\
|
z y x
z y x
z y x
z
y
x
3 6 3
2 4 2
2

d) T: R
4
R
3
; T
|
|
|
.
|
\
|
+ +
+ +
+ +
=
|
|
|
|
|
.
|
\
|
w z x
w z y
w z y x
w
z
y
x
6 6
3 4
3 2
b) En los siguientes ejercicios encuentre A
T
, Ker(T), Img(T), Rng(T), Nul(T).
a) T: R
2
R
2
; T
|
|
.
|
\
|
+
=
|
|
.
|
\
|
y x
y x
y
x
2 3
4
B
1
= B
2
=
)
`
|
|
.
|
\
|
|
|
.
|
\
|
3
4
,
1
1
b) T: R
2
R
3
; T
|
|
|
.
|
\
|
+
=
|
|
.
|
\
|
y
y x
y x
y
x
2 B
1
=
)
`
|
|
.
|
\
|
|
|
.
|
\
|
2
1
,
1
2
B
2
=
|
|
|
.
|
\
|
|
|
|
.
|
\
|
|
|
|
.
|
\
|
5
2
0
,
0
2
0
,
0
1
1
c) T: R
2
R
2
; T
|
|
.
|
\
|
=
|
|
.
|
\
|
y x
x
y
x 2
B
1
=
)
`
|
|
.
|
\
|
|
|
.
|
\
|
1
3
,
2
4
B
2
=
)
`
|
|
.
|
\
|
|
|
.
|
\
|
1
5
,
1
6
d) T: R
3
R
2
; T
)
`
|
|
.
|
\
|
=
|
|
|
.
|
\
|
x
z y
z
y
x
2
B
1
=
|
|
|
.
|
\
|
|
|
|
.
|
\
|
|
|
|
.
|
\
|
3
5
2
,
1
4
2
,
0
1
0
B
2
=
)
`
|
|
.
|
\
|
|
|
.
|
\
|
1
1
,
2
3
e) T: R
3
R
2
; T
|
|
.
|
\
|
=
|
|
|
.
|
\
|
y
x
z
y
x
3
2
B
1
=
|
|
|
.
|
\
|
|
|
|
.
|
\
|
|
|
|
.
|
\
|
1
6
0
,
2
1
0
,
3
1
2
B
2
=
)
`
|
|
.
|
\
|
|
|
.
|
\
|
2
5
,
1
3
f) T: R
2
R
3
; T
|
|
|
.
|
\
|
+ =
|
|
.
|
\
|
0
2
y x x
x
y
x
B
1
=
)
`
|
|
.
|
\
|
|
|
.
|
\
|
2
3
,
4
1
B
2
=
|
|
|
.
|
\
|
|
|
|
.
|
\
|
|
|
|
.
|
\
|
2
1
3
,
5
3
2
,
0
0
1
Diagonalizacin de matrices.
Se plantean los siguientes problemas:
1. Dado un operador lineal V V T : sobre un espacio vectorial V de dimensin
finita, existe una base para V respecto a la cual la matriz de T sea diagonal?
2. Dado un operador lineal V V T : sobre un espacio de productos interiores de
dimensin finita , hay una base ortonormal para V con respecto a la cual la
matriz de T sea diagonal?
O sea, dada una matriz cuadrada A, existe una matriz inversible P tal que P
-1
A P sea
diagonal?
Dada una matriz cuadrada A, hay una matriz ortogonal P tal que P
-1
A P = P
T
A P sea
diagonal?
Se dice que una matriz cuadrada A es diagonalizable si existe una matriz inversible P tal
que P
-1
AP sea diagonal, en este caso, se dice que la matriz P diagonaliza a A.
Teorema: Si A es una matriz cuadrada de orden n , entonces, las proposiciones que siguen
son equivalentes:
i. A es diagonalizable
ii. A tiene n eigenvectores linealmente independientes
El procedimiento para diagonal izar una matriz A es el siguiente:
a) Se hallan n eigenvectores linealmente independientes de A,
n
p p p , ... , ,
2 1
b) Se forma una matriz P que tenga a
n
p p p , ... , ,
2 1
como sus vectores columnas
c) Entonces P
-1
AP ser diagonal con
n
, ... , ,
2 1
como sus elementos sucesivos en la
diagonal, en donde
i
es el eigenvalor correspondiente a
i
p , i = 1, 2, ... , n.
Ejemplo. Halle una matriz P que diagonalice a la matriz
(
(
(

=
5 0 0
0 3 2
0 2 3
A .
Solucin. Primeramente se encuentran los eigenvalores que son 5 y 1 y los eigenvectores
que son
(
(
(
=
(
(
(
=
1
0
0
,
0
1
1
2 1
p p para 5 = y
(
(
(
=
0
1
1
3
p para 1 =
De esta forma, hay tres vectores propios linealmente independientes y por lo tanto la matriz
A es diagonalizable y la matriz que la diagonaliza es
(
(
(
=
0 1 0
1 0 1
1 0 1
P .
Ahora
(
(
(
=
(
(
(
(
(
(

(
(
(
(
(
1 0 0
0 5 0
0 0 5
0 1 0
1 0 1
1 0 1
5 0 0
0 3 2
0 2 3
0
2
1
2
1
1 0 0
0
2
1
2
1
1
AP P .
Ejemplo. Probar que la matriz
(
=
1 2
2 3
A no es diagonalizable.
Solucin. La ecuacin caracterstica es 0
1 2
2 3
=

. Desarrollando este
determinante se tiene que: 1 0 ) 1 ( 0 4 3 3
2 2
= = + = + + + .
Si
(
=
(
=
0
0
2 2
2 2
, 1
2
1
x
x
, de esta forma,
2 1
x x = y un vector propio para 1 = es:
(
=
(
=
1
1
2
2
2
x
x
x
x y por lo tanto una base para el espacio solamente contiene al vector (1,
1). Como solamente hay un vector propio linealmente independiente y la matriz dada es de
orden dos, entonces, la matriz no es diagonalizable.
Teorema. Si
n
v v v , ... , ,
2 1
son eigenvectores de una matriz A correspondientes a
eigenvalores distintos
n
, ... , ,
2 1
entonces el conjunto de los vectores {
n
v v v , ... , ,
2 1
} es
linealmente independiente.
Teorema. Si una matriz A de orden n tiene n eigenvalores distintos, entonces, es
diagonalizable.
Nota: El recproco del teorema es falso, es decir, una matriz A de orden n puede ser
diagonalizable an cuando no tenga n eigenvalores distintos.
Ejemplo. La matriz
(
=
3 0
0 3
A solamente tiene un eigenvalor 3 = , sin embargo, es
diagonalizable, tomando P = I, P
-1
= I, y as, P
-1
A P = I A I = A.
Diagonalizacin ortogonal de matrices.
Se dice que una matriz cuadrada A es ortogonalmente diagonalizable si existe una matriz
ortogonal P tal que P
-1
A P = P
T
A P sea diagonal, en este caso se dice que P diagonaliza
ortogonalmente a la matriz A.
Teorema: Sea A una matriz cuadrada de orden n, las proposiciones siguientes son
equivalentes: i) A es ortogonalmente diagonalizable, ii) A tiene un conjunto ortonormal de
n vectores propios.
Teorema: Una matriz de orden n es ortogonalmente diagonalizable si y slo si A es
simtrica.
En efecto, ntese que si D AP P =
1
, donde D es una matriz diagonal, entonces:
A PDP P D P A PDP A PDP A PDP A PD AP
T T T T T T T T T
= = = = = = =
1 1
) ( ) (
De esta manera, se comprueba que A es una matriz simtrica.
El procedimiento para diagonalizar ortogonalmente una matriz simtrica es el siguiente:
i. Hallar una base para cada espacio propio de A
ii. Aplicar el proceso de Gram-Schmidt a cada una de estas bases a fin de obtener una
base ortonormal para cada espacio propio.
iii. Frmese la matriz P cuyas columnas sean los vectores bases construidos en el paso
anterior, esta matriz diagonaliza ortogonalmente a la matriz A.
Ejemplo. Hallar una matriz ortogonal P que diagonal ice a
(
(
(
=
4 2 2
2 4 2
2 2 4
A .
Solucin. Primero determinamos los valores propios:
0 ) 8 ( ) 2 (
4 2 2
2 4 2
2 2 4
2
= =
. As, los valores propios son 8 , 2 = =

Si
3 2 1 3 2 1
3
2
1
0 2 2 2
0
0
0
2 2 2
2 2 2
2 2 2
: , 2 x x x x x x
x
x
x
tiene se = = + +
(
(
(
=
(
(
(
(
(
(
= .
De esta forma, una base para este espacio propio, la componen los vectores (-1, 1, 0) y (-1,
0, 1) y ortonormalizando esta base nos queda:
)
6
2
,
6
1
,
6
1
( ) 0 ,
2
1
,
2
1
( y .
Si
(
(
(
=
(
(
(
(
(
(
=
0
0
0
4 2 2
2 4 2
2 2 4
: , 8
3
2
1
y
y
y
tiene se
Ejercicios Propuestos
1. Hallar los valores y vectores propios de T
|
|
.
|
\
|
+
+
=
|
|
.
|
\
|
y x
y x
y
x
2
2
2. Diagonalizar T
|
|
|
.
|
\
|
+
+
+
=
|
|
|
.
|
\
|
z y x
z y x
z y x
z
y
x
4 6 6
3 5 3
3 3
3. Diagonalizar
(
(
(
(
1 0 0 1
1 0 0 0
0 1 1 0
0 0 0 2
4. Hallar valores y vectores caractersticos T
|
|
|
.
|
\
|
+
+
=
|
|
|
.
|
\
|
z y
z y
y x
y
x
4 2
2
.
|
|
|
.
|
\
|

2 0 0
0 4 1
0 4 0
EXAMEN
I. Completacin
1. Determinar si las siguientes proposiciones son verdaderas o falsas. Justifique su
respuesta.
a) El conjunto de puntos sobre la recta y = 2 x + 1 para x , representa un espacio
vectorial:__________________________________________
b) Si H
1
y H
2
son subespacios de un espacio vectorial V. Entonces H
1
+ H
2
es
un subespacio de V:___________________________________
c) La condicin para que los vectores
|
|
.
|
\
|
|
|
.
|
\
|
d
c
y
b
a
sean linealmente dependiente
es: ad - bc = 0 para a, b, c y d nmeros
reales:_______________________
d) Los vectores
|
|
|
.
|
\
|
|
|
|
.
|
\
|
|
|
|
.
|
\
|
1
0
0
;
1
1
0
;
1
1
1
generan al espacio vectorial V =
3
:____
II. En las proposiciones siguientes marque la repuesta correcta.
1. Dado un espacio vectorial E si | e E y B = {b
1
, b
2
, b
3
, b
4
} c E y se cumple que para
1,
2
,
3
,
4
son nicos y distintos de cero. | =
1
b
1
+
2
b
2
+
3
b
3
+
4
b
4
entonces:
a) {b
1
, b
2
, b
3
, b
4
} es L.I
b) {b
1
, b
2
, b
3
, b
4
} es L.D
c) {b
1
, b
2
, b
3
} es L.I
d) {b
1
, b
2
, b
3
, b
4
, a} es L.D
2. Una base para el subespacio vectorial, T = {(a, b, c, d) e R
4
| a = c = 0} es el conjunto.
a) {(0, 1, 0, 1), (0, 2, 0, 2)}
b) {(0, 0, 0, 1), (0, 2, 0, 0)}
c) {(0, 2, 0, -1), (0, 1, 0, 3), (0, 1, 0, 1)}
d) {(0, 1, 0, 1)}
3. El ncleo de una T. Lineal f: E F es:
a) N = {x e E | f(x) = 0 , 0 e F}
b) N = {x e E | f(x) = 0, 0 e E}
c) N = {x e E | f(x) e F}
d) N = {x e F | f(x) = 0 , 0 e F}
4. Dado dim E = n, dim F = p y T: E F lineal, si dim N = q y dim f (E) = k, entonces se
cumple la relacin.
a) q = n p
b) k = q + p
c) q = n k
d) q = n + k
5. es un valor propio de una T. L f de E, si existen en E vectores x tales que:
a) f(x) = x ; para todo x
b) f(x) = f(x)
c) f(x) = f(E)
d) f(x) = x ; x = 0
III. Encuentre una base ortonormal utilizando el proceso de Gram Schmidt para el conjunto
de vectores en el plano:

=
|
|
|
.
|
\
|
= 0 2 : z y x
z
y
x
IV. Sea T una transformacin Lineal de

2
3
tal que
|
|
.
|
\
|
|
|
|
.
|
\
|
=
|
|
.
|
\
|
|
|
|
.
|
\
|
=
|
|
.
|
\
|
4
2
5
0
4
5
3
3
2
1
3
1
T encuentre T y T
V. Sea T:
3

3
definida por
|
|
|
.
|
\
|
+
+
+
=
|
|
|
.
|
\
|
=
z y x
z y x
z y x
z
y
x
T
9 3 6
6 2 4
3 2

Halle A
T
; Ker ( T ) : Img ( T ) ; NuL ( T ) ; Rang. ( T )
VI. Diagonalizar T
|
|
|
.
|
\
|
+
+
+
=
|
|
|
.
|
\
|
z y x
z y x
z y x
z
y
x
4 6 6
3 5 3
3 3
VII. Determine si la matriz
|
|
.
|
\
|
=
3 3
2 4
A es diagonalizable. Si lo es encuentre una matriz
C tal que D = C
1
A C
VIII. Dada la matriz A =
|
|
|
.
|
\
|
2 2 2
2 5 4
2 4 5
verifique si A es ortogonalmente diagonalizable. Si lo es
encontrar la matriz C y verificar que D = C
T
A C.

TAREA de Espacios Vectoriales Folleto

Uploaded by

Document Information

Copyright

Available Formats

Share this document

Share or Embed Document

Sharing Options

Did you find this document useful?

Is this content inappropriate?

Copyright:

Available Formats

TAREA de Espacios Vectoriales Folleto

Uploaded by

Copyright:

Available Formats

ESPACIOS VECTORIALES Y TRANSFORMACIONES LINEALES

Elaborado : ROGER ALBERTO GARCIA GUEVARA Pgina 1

ESPACIOS VECTORIALES GENERALES.

v como combinacin lineal de los vectores de la base, es decir,

Esto significa que

. As, los valores propios son 8 , 2 = =

IV. Sea T una transformacin Lineal de

You might also like