Professional Documents
Culture Documents
Basic Geometry
Uploaded by
Muralidharan KrishnamoorthyCopyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Basic Geometry
Uploaded by
Muralidharan KrishnamoorthyCopyright:
Available Formats
Basic Geometry
Basic Geometry - Center for Graphics and Geometric Computing,
Technion
2
Some Linear Algebra
Vectors and inner products
Commutative
Linear operator
Orthogonally
Orthonormality
L
2
-Norm
Normalized vector
v
v
v
v v v
c c b b a a v v
c b a v
=
=
+ + =
=
,
,
, ,
2 1 2 1 2 1 2 1
Basic Geometry - Center for Graphics and Geometric Computing,
Technion
3
Some Linear Algebra
Matrix Multiplication Linear
Transformation
Do not Commute
Vector-Matrix Multiplication
Treat the vector as a 1d matrix.
Observe the right dimensions
(
(
(
(
+ + +
=
(
(
(
(
(
(
(
(
* * * *
* * * *
* * * *
* * *
* * *
* * *
* * *
* * *
* * * *
* * * *
* * * *
dh cg bf ae
h
g
f
e d c b a
A B B A =
| |
(
(
(
(
+ + +
=
(
(
(
(
*
*
*
* * *
* * *
* * *
* * *
dh cg bf ae
h
g
f
e
d c b a
Bv vB=
Basic Geometry - Center for Graphics and Geometric Computing,
Technion
4
Determinants
If A is a [2 x 2] matrix then det(A) = ad-bc
In this case, det(A) = area of parallelogram
defined by vectors (a,c) and (b,d)
General determinate is defined recursively
by minors
minors are computed by eliminating the
row and column of an entry and
computing the determinant on the
residue.
Few reminders
Determinants are multiplicative
|AB|=|A||B|
|A|=|A
T
|
a b
A
c d
(
=
(
1
( 1)
n
i j
nxn ij ij
j
A a M
+
=
=
Basic Geometry - Center for Graphics and Geometric Computing,
Technion
5
Cross products
The cross product of two vectors V
1
and V
2
V
1
=(x
1
,y
1
,z
1
),V
2
=(x
2
,y
2
,z
2
)
is defined (in determinant form)
Meanings
The area of the parallelogram that is defined by V
1
and V
2
The direction of the normal to the plane that is determined by V
1
and V
2
A vector which is orthogonal to both V
1
and V
2
2 2 2
1 1 1 2 1
z y x
z y x
z y x
V V =
|V
1
x V
2
|
V
1
V
2
Basic Geometry - Center for Graphics and Geometric Computing,
Technion
6
Cross Product
Properties
V
1
x V
2
= V
2
x V
1
Reverse the direction.
|V
1
x V
2
|= |V
1
||V
2
|sin(o)
V
1
V
2
o
V
1
x V
2
V
2
x V
1
=
-V
1
x V
2
Basic Geometry - Center for Graphics and Geometric Computing,
Technion
7
Right and Left Coordinate Systems
Question: What is a positive angle of rotation around an axis
specified by a vector ?
Answer: Align your thumb with the vector. Your other fingers
indicate the direction of a positive rotation.
Definition: A three-dimensional left (right) coordinate system is such
that the positive rotation direction around the Z axis using the left
(right) thumb rotates X towards Y.
A three-dimensional left
coordinate system.
A three-dimensional right
coordinate system.
X
Y Y Z X
Z
Basic Geometry - Center for Graphics and Geometric Computing,
Technion
8
Coordinate Systems
Modeling Coordinate System
World Coordinate System
View Coordinate System
Projection Transform
Screen Coordinate System
Basic Geometry - Center for Graphics and Geometric Computing,
Technion
9
Demo
Modeling and World Coordinate Systems
The modeling coordinate system is the coordinate system
where the object is defined (modeled)
Customarily, objects are modeled around the center of axes
Why?
The world coordinate system is the global coordinate
system where all the object reside
To move objects from one coordinates system to the other we
apply transformations on the object
Multiply the vertices of a polygonal object by a proper [4X4]
matrix
Modeling Transform
Basic Geometry - Center for Graphics and Geometric Computing,
Technion
10
View Coordinate System
A coordinate system that is centered on the virtual
camera
All objects in a scene are either in positive (in front of
the camera) or negative (behind) Z
Positions the viewing volume in the world.
After multiplying objects by the viewing matrix, these
objects are transformed from the world coordinate
system to the view (camera) coordinate system
Basic Geometry - Center for Graphics and Geometric Computing,
Technion
11
Projection Transform & screen
coordinates
The location where a 3D object is projected onto a 2D plane
(image).
There are several options there will be discussed during the
lectures
Usually it is preferred to consider normalized projected space
where the projection transform maps to [-1,1]X[-1,1] square
After the projection transform took place, the object is not yet in
device coordinate systems.
These are the integer values
Basic Geometry - Center for Graphics and Geometric Computing,
Technion
12
The complete pipeline
For every vertex V in a polygonal model apply M, the
concatenated matrix which contain all the
transformations.
(
(
(
(
(
(
(
(
(
(
(
(
(
(
(
(
=
` ` ` `
` ` ` `
` ` ` `
` ` ` `
' ' ' ' ' ' ' '
' ' ' ' ' ' ' '
' ' ' ' ' ' ' '
' ' ' ' ' ' ' '
' ' ' '
' ' ' '
' ' ' '
' ' ' '
p o n m
l k j i
h g f e
d c b a
p o n m
l k j i
h g f e
d c b a
p o n m
l k j i
h g f e
d c b a
p o n m
l l j i
h g f e
d c b a
M
Modeling
Matrix
Viewing
Matrix
Projection
Matrix
Screen
Matrix
M V V = '
Basic Geometry - Center for Graphics and Geometric Computing,
Technion
13
Line equations
What are the available forms
Explicit form F(x) = ax +b
Implicit form F(x,y) = ax + by +c = 0
Parametric form F(t) = P
0
+t(P
1
- P
0
)
Applications
A point on a line query
Traverse the line
Rendering
Basic Geometry - Center for Graphics and Geometric Computing,
Technion
14
Point-Line Distance
<(P
0
P
1
),(P-P
2
)> = 0
<(P
0
P
1
),(P
0
+t(P
1
-P
0
)-P
2
)> = 0
Solve for t
Substitute into the first equation to get the value of P.
Find the distance between P and P
2
as usual.
P
P
1
P
0
P
2
(1) :P = P
0
+t(P
1
-P
0
)
2 0 1 0 2 0 1 0 2 0 1 0
1 0 1 0
( )( ) ( )( ) , x x x x y y y y P P P P
t
P P P P
+ < >
= =
Basic Geometry - Center for Graphics and Geometric Computing,
Technion
15
Point-Plane Distance
The projection of the line (P
a
,P
b
) on the normal is
given by:
Substitute the following to solve the equation:
P
a
P
b
P
Ax+By+Cz+D =0
P=(x,y,z)
o
n
( ) ( ) ( )
b a b a b a
A x x B y y C z z
Dist
n
+ +
=
Basic Geometry - Center for Graphics and Geometric Computing,
Technion
16
Line-Line Intersection
1 1 1 1 2 2 2 2
0 1 0 0 1 0
1 2
1 1 1 1 2 2 2 2
0 1 0 0 1 0
( ) ( ) ( ) ( )
[0,1] [0,1]
( ) ( ) ( ) ( )
x t x x x t x r x x x r
L t L r
y t y y y t y r y y y r
= + = +
= e = e
= + = +
At an intersection point, the x and y values are equal in both
representations, forming two linear equations in two unknowns (r,t).
Question: What is the meaning of r,t < 0 or r,t >1 ?
(x
0
1
,y
0
1
)
(x
1
1
,y
1
1
)
(x
1
2
,y
1
2
)
(x
0
2
,y
0
2
)
L
1
L
2
1 1 1 2 2 2
0 1 0 0 1 0
1 1 1 2 2 2
0 1 0 0 1 0
( ) ( )
( ) ( )
x x x t x x x r
y y y t y y y r
+ = +
+ = +
Basic Geometry - Center for Graphics and Geometric Computing,
Technion
17
Linear Operators
Definition: A linear operator, L:AB, satisfies the following:
L(aX+bY) = aL(X) + bL(Y)
Examples
( ) ( ) ( ) ( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
D af x bg x D af x D bg x
aD f x bD g x
+ = +
= +
Scaling
( ) ( ) ( ) ( ) ( ) ( )
( ) ( )
( ) ( ) ( ) ( ) x g bS x f aS
x bsg x asf
x bg x af s x bg x af S
+ =
+ =
+ = +
Differentiation
D(h(x)) = h(x)
S(h(x)) = sh(x)
Question: Is F(X) = oX+| a linear operation ?
Basic Geometry - Center for Graphics and Geometric Computing,
Technion
18
Linear Operators (cont).
Answer: No !!
( )
( )
( ) ( )
( ) ( ) (1 )
( ) ( ) (1 )
F aX bY
aX bY
aX bY
a X b Y
a X b Y a b
aF X bF Y a b
o |
o o |
o o |
o | o | |
|
+
= + +
= + +
= + +
= + + + +
= + +
Definition: An affine operator, A, satisfies:
A(aX+bY) = aA(X) + bA(Y), for a+b = 1
Question: Is F(X) = oX+| an affine operation ?
Basic Geometry - Center for Graphics and Geometric Computing,
Technion
19
Convexity
.
2 1
, 2 For .
1
.
1
of an is
1
say that We
.
1
0 , 1 ,
1
let and points, be
1
Let
P P P n
n
i
i
P CH P
n
i
i
P
i
P
n
i i
a P
n
i i
a
i
a
n
i
i
a n
n
i
i
P
e =
=
e
=
=
=
=
> =
= =
|
|
.
|
\
|
)
`
)
`
)
`
)
`
n combinatio affine
An object 0 is convex iff for any two points
P,Qe0,
tP+(1-t)Qe0, te[0,1].
P
Q
( )Q t tP + 1
0
The convex hull CH(0), of an object 0,
is the minimal convex shape C, such
that 0_C.
C
0
C=CH(0)
Basic Geometry - Center for Graphics and Geometric Computing,
Technion
20
Curves
( ) ( ) ( )
| |
T C t
dC t
dt
x t y t = ' = = ' '
( )
,
C(t) may be thought of as the
trajectory of a point in time.
The unit length tangent vector is
( )
( ) ( ) | |
( ) ( )
2 2
,
t y t x
t y t x
t C T
' + '
' '
= =
( ) t C
( )
dt
t dC
T =
Let C(t)=[x(t),y(t)] te[T
0
,T
1
]
be a continuous uni-
variate parametric curve. The tangent vector is
T=C(t):
C(t) is the velocity vector at
time t.
You might also like
- GTC On GeM 3.0 v1.12Document40 pagesGTC On GeM 3.0 v1.12govind tiwariNo ratings yet
- Grade 1 Maths Revision Ppt-19 FebDocument7 pagesGrade 1 Maths Revision Ppt-19 FebMuralidharan KrishnamoorthyNo ratings yet
- 1671515247nit - Chenab Valley Power Projects (P) Limited (CVPPPL) - Tender Id Cvpppl22-23et1 - Electro-Mechanical (E&m) Works Package (Lot-III) of Kwar He Project 540 MW - Due Date 25.01.2023Document21 pages1671515247nit - Chenab Valley Power Projects (P) Limited (CVPPPL) - Tender Id Cvpppl22-23et1 - Electro-Mechanical (E&m) Works Package (Lot-III) of Kwar He Project 540 MW - Due Date 25.01.2023Muralidharan KrishnamoorthyNo ratings yet
- Cursive Handwriting FreebieDocument10 pagesCursive Handwriting FreebieMuralidharan KrishnamoorthyNo ratings yet
- STD II ENGLISH - Assessment VDocument5 pagesSTD II ENGLISH - Assessment VMuralidharan KrishnamoorthyNo ratings yet
- Demo Cursive Handwriting Practice Set 23159175Document1 pageDemo Cursive Handwriting Practice Set 23159175Muralidharan KrishnamoorthyNo ratings yet
- Readers Digest Feb 2020 PDFDocument148 pagesReaders Digest Feb 2020 PDFMuralidharan KrishnamoorthyNo ratings yet
- Pragati Millets Booklet 25.10Document136 pagesPragati Millets Booklet 25.10Muralidharan KrishnamoorthyNo ratings yet
- ABSLI Capped Nifty Index FundDocument1 pageABSLI Capped Nifty Index FundMuralidharan KrishnamoorthyNo ratings yet
- Ratnam-Ball Pens-2019-2Document2 pagesRatnam-Ball Pens-2019-2Muralidharan KrishnamoorthyNo ratings yet
- Eligible Bank List: Pbank - Name Pbank - NameDocument1 pageEligible Bank List: Pbank - Name Pbank - NameMuralidharan KrishnamoorthyNo ratings yet
- 4test: Free Valid Test Questions and Dumps PDF For Certification Test PrepDocument7 pages4test: Free Valid Test Questions and Dumps PDF For Certification Test PrepMuralidharan KrishnamoorthyNo ratings yet
- Joankaylor Com Thank You For Being A StudentDocument1 pageJoankaylor Com Thank You For Being A StudentMuralidharan KrishnamoorthyNo ratings yet
- Giri Book Isbn List 08.12.17Document43 pagesGiri Book Isbn List 08.12.17Muralidharan KrishnamoorthyNo ratings yet
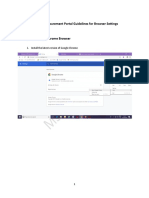
- Install Component Guide - For Chrome, Mozilla PDFDocument10 pagesInstall Component Guide - For Chrome, Mozilla PDFMuralidharan KrishnamoorthyNo ratings yet
- Science&TechnologyDocument31 pagesScience&TechnologyMuralidharan KrishnamoorthyNo ratings yet
- Modern Baby Names PDFDocument113 pagesModern Baby Names PDFvenkateshsj100% (2)
- RTGS Mandate FormDocument1 pageRTGS Mandate Formsaravananji665No ratings yet
- Hindu Baby Girl Names in Kerala PDF Hindu Baby Girl Names in Kerala PDFDocument3 pagesHindu Baby Girl Names in Kerala PDF Hindu Baby Girl Names in Kerala PDFMuralidharan KrishnamoorthyNo ratings yet
- Male Muslim NamesDocument6 pagesMale Muslim NamesBilal KhanNo ratings yet
- Verb To Be - Verb To Be 3Document3 pagesVerb To Be - Verb To Be 3Muralidharan KrishnamoorthyNo ratings yet
- Physically Handicapped Phy14017 - 16 - 2002 - Estt - RR-13032002 PWDLDocument3 pagesPhysically Handicapped Phy14017 - 16 - 2002 - Estt - RR-13032002 PWDLMuralidharan KrishnamoorthyNo ratings yet
- Prep4Sure: Real Exam & Prep4Sureexam Is For Well Preparation of It ExamDocument7 pagesPrep4Sure: Real Exam & Prep4Sureexam Is For Well Preparation of It ExamMuralidharan KrishnamoorthyNo ratings yet
- Uom Ug2017Document122 pagesUom Ug2017GOWTHAMNo ratings yet
- Install Component Guide - For Chrome, Mozilla PDFDocument10 pagesInstall Component Guide - For Chrome, Mozilla PDFMuralidharan KrishnamoorthyNo ratings yet
- Grade 1 EVS Worksheet 1 - Chapter 2Document2 pagesGrade 1 EVS Worksheet 1 - Chapter 2Muralidharan Krishnamoorthy100% (1)
- Grade 1 EVS Answer Key Worksheet 1 - Chapter 2Document2 pagesGrade 1 EVS Answer Key Worksheet 1 - Chapter 2Muralidharan KrishnamoorthyNo ratings yet
- Thank You For Installing Bullzip PDF Printer: Like Us?Document2 pagesThank You For Installing Bullzip PDF Printer: Like Us?Muralidharan KrishnamoorthyNo ratings yet
- Grade 1 EVS Hands On Activity Chapter 3-Parts of A PlantDocument1 pageGrade 1 EVS Hands On Activity Chapter 3-Parts of A PlantMuralidharan KrishnamoorthyNo ratings yet
- Answer The Following Questions:: Class: I Worksheet 4 Name: Subject: EVS Chapter 3: Parts of A PlantDocument2 pagesAnswer The Following Questions:: Class: I Worksheet 4 Name: Subject: EVS Chapter 3: Parts of A PlantMuralidharan KrishnamoorthyNo ratings yet
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeFrom EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeRating: 4 out of 5 stars4/5 (5794)
- Shoe Dog: A Memoir by the Creator of NikeFrom EverandShoe Dog: A Memoir by the Creator of NikeRating: 4.5 out of 5 stars4.5/5 (537)
- The Yellow House: A Memoir (2019 National Book Award Winner)From EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Rating: 4 out of 5 stars4/5 (98)
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceFrom EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceRating: 4 out of 5 stars4/5 (895)
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersFrom EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersRating: 4.5 out of 5 stars4.5/5 (344)
- The Little Book of Hygge: Danish Secrets to Happy LivingFrom EverandThe Little Book of Hygge: Danish Secrets to Happy LivingRating: 3.5 out of 5 stars3.5/5 (399)
- Grit: The Power of Passion and PerseveranceFrom EverandGrit: The Power of Passion and PerseveranceRating: 4 out of 5 stars4/5 (588)
- The Emperor of All Maladies: A Biography of CancerFrom EverandThe Emperor of All Maladies: A Biography of CancerRating: 4.5 out of 5 stars4.5/5 (271)
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaFrom EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaRating: 4.5 out of 5 stars4.5/5 (266)
- Never Split the Difference: Negotiating As If Your Life Depended On ItFrom EverandNever Split the Difference: Negotiating As If Your Life Depended On ItRating: 4.5 out of 5 stars4.5/5 (838)
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryFrom EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryRating: 3.5 out of 5 stars3.5/5 (231)
- On Fire: The (Burning) Case for a Green New DealFrom EverandOn Fire: The (Burning) Case for a Green New DealRating: 4 out of 5 stars4/5 (73)
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureFrom EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureRating: 4.5 out of 5 stars4.5/5 (474)
- Team of Rivals: The Political Genius of Abraham LincolnFrom EverandTeam of Rivals: The Political Genius of Abraham LincolnRating: 4.5 out of 5 stars4.5/5 (234)
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyFrom EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyRating: 3.5 out of 5 stars3.5/5 (2259)
- The Unwinding: An Inner History of the New AmericaFrom EverandThe Unwinding: An Inner History of the New AmericaRating: 4 out of 5 stars4/5 (45)
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreFrom EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreRating: 4 out of 5 stars4/5 (1090)
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)From EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Rating: 4.5 out of 5 stars4.5/5 (120)
- Her Body and Other Parties: StoriesFrom EverandHer Body and Other Parties: StoriesRating: 4 out of 5 stars4/5 (821)
- Introduction and Assessment of The Renal - Urological SystemDocument182 pagesIntroduction and Assessment of The Renal - Urological SystemValerie Suge-Michieka100% (1)
- Criminal Law Book 2 Titles 1-8Document146 pagesCriminal Law Book 2 Titles 1-8Minato NamikazeNo ratings yet
- Grandinetti - Document No. 3Document16 pagesGrandinetti - Document No. 3Justia.comNo ratings yet
- Maxima Book Chapter 4Document43 pagesMaxima Book Chapter 4prakush_prakushNo ratings yet
- Internetworking Concepts Overview: © 1999, Cisco Systems, IncDocument50 pagesInternetworking Concepts Overview: © 1999, Cisco Systems, IncShashi Kant RaviNo ratings yet
- Contoh Writing AdfelpsDocument1 pageContoh Writing Adfelpsmikael sunarwan100% (2)
- GRADE 11 Gen Math Inverse FunctionsDocument13 pagesGRADE 11 Gen Math Inverse FunctionsAiejhay Bordaje100% (1)
- The Discovery of The Tun Huang Library and Its Effect On Chinese StudiesDocument21 pagesThe Discovery of The Tun Huang Library and Its Effect On Chinese Studiesfabricatore_21639575No ratings yet
- AIX CommandsDocument8 pagesAIX CommandsKamal KantNo ratings yet
- Energy Management Principles and PracticesDocument102 pagesEnergy Management Principles and PracticesConnor ReedNo ratings yet
- Power Semiconductor DevicesDocument11 pagesPower Semiconductor DevicesBhavesh Kaushal100% (1)
- 332-Article Text-1279-1-10-20170327Document24 pages332-Article Text-1279-1-10-20170327Krisdayanti MendrofaNo ratings yet
- 9709 w06 Ms 6Document6 pages9709 w06 Ms 6michael hengNo ratings yet
- Two Steps From Hell Full Track ListDocument13 pagesTwo Steps From Hell Full Track ListneijeskiNo ratings yet
- Mythbusters - Archimedes Cannon QuestionsDocument2 pagesMythbusters - Archimedes Cannon QuestionsVictoria RojugbokanNo ratings yet
- 2nd YearDocument46 pages2nd YearRajnish DeoNo ratings yet
- Levels of Curriculum PlanningDocument3 pagesLevels of Curriculum Planningysndnl0% (1)
- Case Digest 1-4.46Document4 pagesCase Digest 1-4.46jobelle barcellanoNo ratings yet
- Entrepreneurial Culture - Chapter 13Document11 pagesEntrepreneurial Culture - Chapter 13bnp guptaNo ratings yet
- Isl Isl StyleguideDocument50 pagesIsl Isl StyleguideCole FranklinNo ratings yet
- Kashida Embroidery: KashmirDocument22 pagesKashida Embroidery: KashmirRohit kumarNo ratings yet
- Torts and Damages Midterm ReviewerDocument25 pagesTorts and Damages Midterm ReviewerErika-Anne ThereseNo ratings yet
- Fossils (DK Smithsonian Handbook) by DKDocument320 pagesFossils (DK Smithsonian Handbook) by DKAnthony Mello71% (7)
- Dwnload Full Social Psychology 4th Edition Gilovich Test Bank PDFDocument35 pagesDwnload Full Social Psychology 4th Edition Gilovich Test Bank PDFalilonghidotardlyq71i7f100% (8)
- TestDocument21 pagesTestTri Arini TitisingtyasNo ratings yet
- Create and Open Input Dialog Box - MATLAB InputdlgDocument4 pagesCreate and Open Input Dialog Box - MATLAB InputdlgwhytheritoNo ratings yet
- Syntax Made Easy (Roberta D'Alessandro)Document23 pagesSyntax Made Easy (Roberta D'Alessandro)John DoeNo ratings yet
- Online Sales of New Cars: StudyDocument29 pagesOnline Sales of New Cars: StudyIson StudiosNo ratings yet
- Odisha State Museum-1Document26 pagesOdisha State Museum-1ajitkpatnaikNo ratings yet
- STaD 01 C 4Document4 pagesSTaD 01 C 4rogeraccuraNo ratings yet