OXFORD UNIVERSITY PRESS

MOCK 13(I) COMPULSORY PART PAPER 1 SOLUTION

Oxford University Press 2013 P.1
Compulsory Part Paper 1
Solution Marks

1.

3 3 1
2 4
) ( y x
y x

=
9 3
2 4
y x
y x

= x
4 + 3
y
2 9

=
7
1
xy




1M
1M
1A
----------(3)

2.

a
ab
+

1
2 3
= 3 b
3 2ab = (3 b)(1 + a)
3 2ab = 3 + 3a b ab
b = ab + 3a
b = a(b + 3)
a =
3 + b
b



1M

1M

1A
----------(3)

3. (a) 16m
2
9n
2

= (4m)
2
(3n)
2
= (4m + 3n)(4m 3n)


1A

(b)
4m 3n 16m
2
+ 9n
2

= (4m 3n) (16m
2
9n
2
)
= (4m 3n) (4m + 3n)(4m 3n)
= (4m 3n)(1 4m 3n)


1M
1A
----------(3)

4. (a) Let $x be the cost of the tablet computer.
x(1 + 30%) = 4 940
x =
% 30 1
940 4
+

= 3 800
The cost of the tablet computer is $3 800.

1M


1A

OXFORD UNIVERSITY PRESS
MOCK 13(I) COMPULSORY PART PAPER 1 SOLUTION

Oxford University Press 2013 P.2
Solution Marks
(b) Selling price at a discount of 20%
= $4 940 (1 20%)
= $3 952
> $3 800
i.e. He can still make a profit.
The claim is agreed.

1M




1A
----------(4)

5. Suppose x child tickets of that train are sold each day.
Then (13 1 000 x) adult tickets of that train are sold each day.
90x + 150(13 1 000 x) = 1 716 000
90x + 1 950 000 150x = 1 716 000
60x = 234 000
x = 3 900
The number of child tickets of that train sold each day is 3 900.



1A
1M + 1A


1A

----------(4)

6. (a)

2
2 + x
> 3(x 4)

2
2 + x
> 3x + 12
x + 2 > 6x + 24
x + 6x > 24 2
7x > 22
x >
7
22







1M

1A
(b)
1 7x s 13
12 s 7x
x >
7
12

x >
7
22
or x >
7
12

i.e. x >
7
12

The required smallest integer is 1.



1A




1A
----------(4)


OXFORD UNIVERSITY PRESS
MOCK 13(I) COMPULSORY PART PAPER 1 SOLUTION

Oxford University Press 2013 P.3
Solution Marks
7. ZAOD = 90 + 36
= 126
ZACD =
2
126

= 63
ZODC = 36
In CDF,
ZAFO = 63 + 36
= 99
In AFO,
ZOAC + 99 = 126
ZOAC = 27



1M


1A

1M



1A
----------(4)

8. (a) A' = (3 , 360 60)
= (3 , 300)
B' = (4 , 120 + 90)
= (4 , 210)


1A

1A
(b) ZA'OB' = 300 210
= 90


1A
(c) ZAOB = 120 60
= 60
Height above OB = OA sin 60
Height above OB' = OA'
We have
area of AOB =
2
1
OB OA sin 60
and area of A'OB' =
2
1
OB' OA'
OA = OA', OB = OB' and sin 60 < 1
The area of A'OB' is greater than the area of AOB.
i.e. A'OB' has a greater area.






1M



1A
----------(5)

OXFORD UNIVERSITY PRESS
MOCK 13(I) COMPULSORY PART PAPER 1 SOLUTION

Oxford University Press 2013 P.4
Solution Marks
9. (a)
Radius of the sphere =
2
18
cm = 9 cm
Inner radius of the container = radius of the sphere = 9 cm
Volume of the water poured into the container
= |
.
|

\
|

3 2
9
3
4
18 9 cm
3
= 486t cm
3




1A

1M
1A

(b) Let h cm be the height of the water in the container.
t 9
2
h = 486t
h = 6
The height of the water in the container is 6 cm.

1M
1A

----------(5)

10. (a) f(x) = (x 2)(x
2
3x + 4) + r
f(x) (x 1)g(x)
x 1 is a factor of f(x).
By the factor theorem,
f(1) = 0
(1)(1 3 + 4) + r = 0
r = 2
1A



1M

1A
----------(3)

(b) f(x) = (x 2)(x
2
3x + 4) + 2
= x
3
5x
2
+ 10x 6
= (x 1)(x
2
4x + 6)

g(x) = x
2
4x + 6

Consider x
2
4x + 6 = 0.
A = (4)
2
4(1)(6)
= 8
< 0
i.e. All the roots of the equation g(x) = 0 are not real numbers.
The claim is agreed.


1M

1A



1M



1A
----------(4)

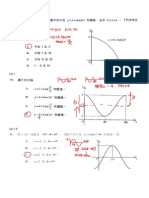
11. (a) Median = 58
Inter-quartile range = 68 50
= 18
1A

1A
----------(2)

x
3
5x
2
+ 10x 6 )
x
3
x
2

x
2
4x + 6
4x
2
+ 10x
4x
2
+ 4x
6x 6
x 1
6x 6
OXFORD UNIVERSITY PRESS
MOCK 13(I) COMPULSORY PART PAPER 1 SOLUTION

Oxford University Press 2013 P.5
Solution Marks
(b)

1A
for the
median
1A
for all correct
----------(2)

(c) Since the 7 students who scored the lowest marks in the first English test may
not be the 7 students who score the lowest marks in the second English test,
we cannot conclude that the 1st quartile of the scores in the second test is
greater than that in the first test.
The claim is disagreed.




1M
1A
----------(2)


12. (a) Let C = k
1
p + k
2
t
2
, where k
1
and k
2
are non-zero constants.
When p = 60 and t = 0.5, C =
000 2
400 3
.

000 2
400 3
= k
1
(60) + k
2
(0.5)
2

1.7 = 60k
1
+ 0.25k
2
..................................................... (1)
When p = 90 and t = 0.75, C =
000 1
700 2
.

000 1
700 2
= k
1
(90) + k
2
(0.75)
2

2.7 = 90k
1
+ 0.562 5k
2
................................................. (2)
(1) 1.5: 2.55 = 90k
1
+ 0.375k
2
................................................ (3)
(2) (3): 0.15 = 0.187 5k
2

k
2
= 0.8
Substitute k
2
= 0.8 into (1).
1.7 = 60k
1
+ 0.25(0.8)
k
1
= 0.025
C = 0.025p + 0.8t
2

When p = 100 and t = 0.8,
C = 0.025(100) + 0.8(0.8)
2

= 3.012
The required total cost
= $3 000 3.012
= $9 036


1A















1A

1M



1A
----------(5)
1M
either one
40 50 60 70 80 90
Score
OXFORD UNIVERSITY PRESS
MOCK 13(I) COMPULSORY PART PAPER 1 SOLUTION

Oxford University Press 2013 P.6
Solution Marks
(b) Cost of each notebook = $
000 1
200 3
= $3.2
3.2 = 0.025(120) + 0.8t
2

t
2
= 0.25
t = 0.5 or 0.5 (rejected)
The required thickness is 0.5 cm.


1M

1A
----------(2)

13. (a) Let cm be the slant height of the cone.
2 2
6 . 3 8 . 4 + =
= 6
Curved surface area
= t 3.6 6 cm
2

= 21.6t cm
2






1M
1A
----------(2)


(b)(i) Maximum absolute error =
2
1 . 0
cm = 0.05 cm
Least possible value of the height = 3.55 cm
Least possible value of the base radius = 4.75 cm
Least possible value of the total surface area
= (t 3.55
2
+ t 3.55
2 2
55 . 3 75 . 4 + ) cm
2

~ 105.73 cm
2

< 120 cm
2

The claim is disagreed.






1M + 1A


1A
(ii)
95
96
4.75
4.8
of Height
of Height
= =
B
A

71
72
3.55
3.6
of radius Base
of radius Base
= =
B
A


B
A
B
A
of radius Base
of radius Base
of Height
of Height
=
A and B are not similar solids.





1M

1A
----------(5)

14. (a) Coordinates of A = |
.
|

\
|

2
6
,
2
8

= (4 , 3)

1A
----------(1)

OXFORD UNIVERSITY PRESS
MOCK 13(I) COMPULSORY PART PAPER 1 SOLUTION

Oxford University Press 2013 P.7
Solution Marks
(b)(i)
I is the perpendicular bisector of AB. 1A

(ii)
Let (x , y) be the coordinates of P.
PA = PB

2 2
) 3 ( ) 4 ( + y x =
2 2
)] 1 ( [ ) 6 ( + y x

2 2
) 3 ( ) 4 ( + y x = (x 6)
2
+ (y + 1)
2

x
2
8x + 16 + y
2
6y + 9 = x
2
12x + 36 + y
2
+ 2y + 1
4x 8y 12 = 0
x 2y 3 = 0
The equation of I is x 2y 3 = 0.



1M + 1A




1A

Alternative Solution
Coordinates of the mid-point of AB = |
.
|

\
| + +
2
) 1 ( 3
,
2
6 4

= (5 , 1)
Slope of AB =
4 6
3 1

= 2
AB I
Slope of I =
2
1

=
2
1

The equation of I is
y 1 =
2
1
(x 5)
2y 2 = x 5
x 2y 3 = 0













1M + 1A

1A
----------(4)

(c) I is the perpendicular bisector of AB.
Perpendicular distance from A to I = perpendicular distance from B to I
Area of AHK
= HK
2
1
perpendicular distance from A to I
= HK
2
1
perpendicular distance from B to I
= area of BHK
Area of AHK = area of BHK
Area of AHK : area of BHK = 1 : 1


1M





1M

1A
----------(3)

OXFORD UNIVERSITY PRESS
MOCK 13(I) COMPULSORY PART PAPER 1 SOLUTION

Oxford University Press 2013 P.8
Solution Marks
15. (a) The required probability
=
7
7
2
2
6
6
P
P P

=
7
2


1M

1A
----------(2)

(b) The required probability
=
7
3
5
1
2
2
5
2
2
1
C
C C C C +

=
35
25

=
7
5


1M



1A

Alternative Solution
The required probability
= 1
7
3
5
3
C
C

= 1
35
10

=
7
5





1M

1A
----------(2)

16. (a)
Let s marks be the standard deviation of the scores in the test.

s
62 60
= 0.4
s = 5
Standard score of Bruce in the test
=
5
62 64

= 0.4







1A
----------(2)

1M
either one

OXFORD UNIVERSITY PRESS
MOCK 13(I) COMPULSORY PART PAPER 1 SOLUTION

Oxford University Press 2013 P.9
Solution Marks
(b) Consider the mean score of the class.

2
65 59+
= 62
i.e. The mean score of the two students who quit the school is the same as
the original mean score of the class.
The mean score of the class remains unchanged after the two scores are
removed.

Consider the standard deviation of the test scores.
Original variance = 5
2
= 25
(59 62)
2
= 9 < 25
(65 62)
2
= 9 < 25
The squares of the differences between the scores of the two students who
quit the school and the mean are both less than the original variance, while
the number of students decreases by 2.
The variance of the test scores will increase after the two scores are
removed.
i.e. The standard deviation of the test scores will increase.
The standard score of Bruce will decrease.
i.e. The standard score of Bruce will change.







1M










1M

1A
----------(3)

17. (a) Let G be the centre of the circle C.
Coordinates of G = |
.
|

\
|

2
4
,
2
6

= (3 , 2)
Slope of AG =
3 1
) 2 ( 1

=
2
1

Slope of the tangent at A = 2
The equation of the tangent is
y (1) = 2(x 1)
y + 1 = 2x 2
2x y 3 = 0










1M

1A
----------(2)

OXFORD UNIVERSITY PRESS
MOCK 13(I) COMPULSORY PART PAPER 1 SOLUTION

Oxford University Press 2013 P.10
Solution Marks
(b)(i)







The equation of L is y = 2x + b.
Substitute y = 2x + b into the equation of the circle.
x
2
+ (2x + b)
2
6x + 4(2x + b) + 8 = 0
x
2
+ 4x
2
+ 4xb + b
2
6x + 8x + 4b + 8 = 0
5x
2
+ (4b + 2)x + b
2
+ 4b + 8 = 0
Discriminant of the above equation
= (4b + 2)
2
4(5)(b
2
+ 4b + 8)
= 16b
2
+ 16b + 4 20b
2
80b 160
= 4b
2
64b 156
L and C intersect at two points.
4b
2
64b 156 > 0
b
2
+ 16b + 39 < 0
(b + 3)(b + 13) < 0
13 < b < 3
1M







1A




1A

(ii) Let y = 2x + k be the equation of L'.
From (b)(i), we have
5x
2
+ (4k + 2)x + k
2
+ 4k + 8 = 0
Product of the two roots of the above equation = 4
4
5
8 4
2
=
+ + k k

k
2
+ 4k + 8 = 20
k
2
+ 4k 12 = 0
(k + 6)(k 2) = 0
k = 6 or 2 (rejected)
The equation of L' is y = 2x 6.





1M





1A
----------(5)

18. (a) In ABD,
BD =
2 2
9 15 cm
= 12 cm



1A

Alternative Solution
In BCD,
BD =
2 2
5 13 cm
= 12 cm



1A

----------(1)

OXFORD UNIVERSITY PRESS
MOCK 13(I) COMPULSORY PART PAPER 1 SOLUTION

Oxford University Press 2013 P.11
Solution Marks
(b)(i) In ABC,
AC
2
= AB
2
+ BC
2
2(AB)(BC) cos ZABC
AC = + 30 cos ) 13 )( 15 ( 2 13 15
2 2
cm
~ 7.500 006 168 cm
= 7.50 cm, cor. to 3 sig. fig.
The length of the piece of plastic rod is 7.50 cm.




1M


1A


(ii) s =
2
168 006 500 . 7 5 9 + +
cm
~ 10.750 003 08 cm
Area of ACD
= ) )( )( ( AC s DC s AD s s
~ 18.749 911 18 cm
2

= 18.7 cm
2
, cor. to 3 sig. fig.




1M

1A
----------(4)

(c) Let h cm be the height of ACD above AD.

2
9 h
~ 18.749 911 18
h = 4.17, cor. to 3 sig. fig.
> 4
The perpendicular distance from C to AD is larger than the height of the
box.
Mary cannot put the paper model completely into the box.



1M





1A
----------(2)

19. (a)(i) When n = 1,
k + 1 000a = 363 900 . (1)
When n = 2,
k + 1 000a
2
= 364 650 (2)
(2) (1): 1 000a
2
1 000a = 750
4a
2
4a 3 = 0
(2a 3)(2a + 1) = 0
a = 1.5 or 0.5 (rejected)
Substitute a = 1.5 into (1).
k + 1 000(1.5) = 363 900
k = 362 400





1M


1A


1A

OXFORD UNIVERSITY PRESS
MOCK 13(I) COMPULSORY PART PAPER 1 SOLUTION

Oxford University Press 2013 P.12
Solution Marks
(ii) W(n) = 362 400 + 1 000(1.5)
n

% 100
) 1 (
) 1 ( ) (

n W
n W n W
> 40%
% 100
1
1
) 5 . 1 ( 000 1 400 362
] ) 5 . 1 ( 000 1 400 362 [ ) 5 . 1 ( 000 1 400 362

+
+ +
n
n n
> 40%
1 000(1.5)
n
1 000(1.5)
n 1
> 144 960 + 400(1.5)
n 1

1 000(1.5)
n 1
(1.5 1.4) > 144 960
1.5
n 1
> 1 449.6
(n 1)log 1.5 > log 1 449.6
n 1 > 17.952 328 79
n > 18.952 328 79
Starting from the 19th year, the weight of waste that P needs to handle
will increase by more than 40% annually.






1M




1M



1A
----------(6)

(b)(i) Total weight of waste handled by P in the first n years
= [(k + 1 000a) + (k + 1 000a
2
) + + (k + 1 000a
n
)] tonnes
= [nk + 1 000(a + a
2
+ + a
n
)] tonnes
=
(

+
1
) 1 ( 000 1
a
a a
nk
n
tonnes
=
(

+
1 5 . 1
) 1 5 . 1 )( 5 . 1 ( 000 1
400 362
n
n tonnes
= [362 400n + 3 000(1.5
n
1)] tonnes







1M

1A

(ii) Total weight of waste handled by P in the first 18 years
= [362 400(18) + 3 000(1.5
18
1)] tonnes
~ 10 953 875.64 tonnes
= 10 953 876 tonnes, cor. to the nearest tonne




1A
----------(3)

OXFORD UNIVERSITY PRESS
MOCK 13(I) COMPULSORY PART PAPER 1 SOLUTION

Oxford University Press 2013 P.13
Solution Marks
(c) W(19)
= 362 400 + 1 000(1.5)
19

~ 2 579 237.82

Upper limit of the weight of waste in the 19th year
= [700 000 + (19 1)(100 000)] tonnes
= 2 500 000 tonnes
< 2 579 237.82 tonnes
The weight of waste exceeds the limit that P can handle in the 19th year.
2 579 237.82 40%
= 1 031 695.128
> 100 000
By (a)(ii), the weight of waste exceeds the limit that P can handle in
every subsequent year after the 19th year.
The claim is agreed.





1M





1M


1A
----------(3)

)