24 MACROMOLECULES

2.1.2 The Gaussian Chain Model

Important Concepts: uctuating bond, Hamiltonian for the
Gaussian Chain Model
We consider a chain made up of orientationally uncorrelated (freely-jointed) links
where the length of any link vector is no longer constant but has a probability
distribution
G(r) =
_
3
2b
2
_
3/2
exp
_

3r
2
2b
2
_
(2.36)
with the expectation for the link length being
< r
2
>= b
2
. (2.37)
The probability distribution for the end-to-end vector is then
P(R
e
) = P({r
n
}) (2.38)
=
N

n=1
_
3
2b
2
_
3/2
exp
_

3r
2
n
2b
2
_
(2.39)
=
_
3
2b
2
_
3/2
exp
_

n=1
3(R
n
R
n1
)
2
2b
2
_
(2.40)
and hence for the entropy
S = lnP =
N

n=1
ln P(r
n
) (2.41)
= const
3
2b
2
N

n=1
r
2
n
. (2.42)
From this we obtain the free energy
F({r
n
}) = E +
3T
2b
2
N

n=1
r
2
n
(2.43)
with the internal energy E being independent of {r
n
}.
Prof. Heermann, Heidelberg University
2.1 GENERAL PROPERTIES OF MACROMOLECULES 25
Hence we obtain the same equilibrium distribution as for the freely-jointed chain.
Eq (2.40) also results if we start off with the Hamiltonian for a chain of springs
H =
3
2
k
B
T
b
2
N

n=1
(R
n
R
n1
)
2
(2.44)
and we also obtain the scaling of the end-to-end distance
< R
2
e
> N . (2.45)
Further Reading 2.1.4 (Continuous scales)
For the later development we note the generalization to all scales for the Gaussian
model at xed contour length L
P(R) =
_
r(L)=R
r(0)=0
D[r(s)] exp
_
3L
2b
2
_
L
0
ds
_
r(s)
s
_
2
_
, (2.46)
where r(s) denotes the contour or conformation of the chain. This is solved by
P(R) =
_
3
2b
2
_
3/2
exp
_

3R
2
2b
2
_
(2.47)
and is the proper continuum limit of the FJC, where the limits N and b 0
were taken, such that Nb
2
stayed nite.
We further generalize the effective Hamiltonian
H =
3
2
k
B
T
b
2
_
L
0
ds r
2
(s) (2.48)
where the derivation is to be taken along the contour.
2.1.3 Worm-like Chain Model
Important Concepts: bending rigidity and the relation with the
persistence length
A short-coming of the above models (besides they being phantom chains, i.e.
no self-avoidance) is that there is no intrinsic stiffness. Intuitively, we expect a
bending of the chain to cost energy. A model that provides this is the worm-like
chain model (WLC)
Prof. Heermann, Heidelberg University
26 MACROMOLECULES
R(s)
r(s)
r
n
r
n+1
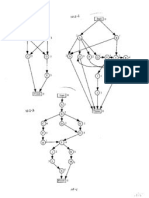
Figure 2.10: Denition of the coordinates used to describe the chain as a con-
tinuous curve
H =
N1

n=1
r
n
r
n+1
(2.49)
which is simply the one-dimensional Heisenberg model for ferromagnets. Here
|r
n
| = b. This model can be treated in the continuum limit where N , b 0
and with
/N = constant , (2.50)
keeping the contour length also constant. Using
r
n+1
r
n
=
1
2
[(r
n
r
n+1
)
2
2b
2
] (2.51)
we have
H = lim
b0,,N
b
2
N1

n=1
b
_
r
n
r
n+1
b
_
2
. (2.52)
To cross over to the continuum limit we use the tangent vector with the arc length
s
r(s)
s
= lim
b0
_
r
n+1
r
n
b
_
(2.53)
Prof. Heermann, Heidelberg University
2.1 GENERAL PROPERTIES OF MACROMOLECULES 27
and

N1
n=1
b
_
L
0
ds to nd
H =

2
_
L
0
ds
_
r(s)
s
_
2
=

2
_
L
0
ds
_

2
R(s)
s
2
_
2
(2.54)
with the bending modulus = b.
Thus the partition function is given by
Z =
_
D[r(s)](|r(s)| 1)exp(H[r(s)]) . (2.55)
The bending modulus must have a relation with the persistence length. To nd
this relation we need to calculate the correlation function
< r(s)r(s

) > exp(|s s

|/
p
) . (2.56)
We can nowcalculate the mean squared end-to-end-distance and the mean squared
radius of gyration
< R
2
e
> = <
__
L
0
dsr(s)
_
2
> (2.57)
=
_
L
0
ds
_
L
0
ds

< r(s) r(s

) > (2.58)
= 2
2
p
_
L

p
1 + e
L/p
_
(2.59)
= L
2
f
D
_
L

p
_
, (2.60)
where f
D
(x) = 2(x 1 + e
x
)/x
2
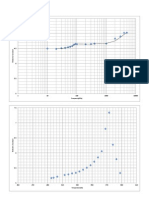
being the Debye-function (see gure 2.11).
Further Reading 2.1.5 (Lattice Chains)
We can also go about calculating the average end-to-end distance staying discrete
(Kratky-Porod model [36] ). For this we write
H =
N1

n=1
r
n
r
n+1
=
N

n=1
cos
n
. (2.61)
The partition function is given by
Z
N
=
N

n=1
_
d
n
e
cos n
= Q
N
l
(2.62)
Prof. Heermann, Heidelberg University
28 MACROMOLECULES
30 10
x
60 40 50
fd(x)
1
0,8
0,6
20
0,4
0,2
0
TheDebyefunction
Figure 2.11: The Debye-function
with
Q
l
= 2
_
1
1
d(cos)e
cos
= 4
sinh

. (2.63)
With this we can calculate the distance
< R
2
e
>= b
2
< (

r
n
)
2
>= b
2

n,m
< r
n
r
m
> (2.64)
again as the correlation between the directions of bonds. For the nearest neighbour
correlation we have
< r
n
r
n+1
> = < cos > (2.65)
=
_
dcos e
cos
_
de
cos
(2.66)
=
d lnQ
l
d()
(2.67)
= coth() 1/ (2.68)
= f
L
() , (2.69)
where f
L
is the Langevin function. In general the correlation is given by [37]
Prof. Heermann, Heidelberg University
2.1 GENERAL PROPERTIES OF MACROMOLECULES 29
< r
n
r
n+1
>= e
N ln(1/c)
, (2.70)
which can be written in terms of the persistence length
p
< r
n
r
n+1
>= e
Nb/p
(2.71)
with

p
=
b
ln(1/c)
(2.72)
If the macromolecule is stiff >> 1 and
c 1 k
B
T/ , (2.73)
then
ln(1/c) k
B
T/ (2.74)
and thus

p
= b . (2.75)
Let us rewrite the end-to-end distance in terms of c
1
b
2
< R
2
e
>=
N

i=1
_
i1

j=1
c
ij
+ 1 +
N

j=i+1
c
ji
_
, (2.76)
then for most i the two sums in the braces can be replaced by

k=1
=
c
1c
and
with this we obtain
< R
2
e
> Nb
2
_
1 +
2c
1 c
_
= Nb
2
1 + c
1 c
. (2.77)
1+c
1c
is the Flory factor. The Kuhn segment length l
K
is then given by
l
K
=
1 + c
1 c
b . (2.78)
Prof. Heermann, Heidelberg University
30 MACROMOLECULES
P
b
t
n
b
t
n
P`
Figure 2.12: Motion of the Fernet triad along a curve
Since we are dealing in some sense with mathematical curves in three dimen-
sional space recall that a curve in space is mathematically determined by the two
parameters: curvature and torsion ( the basic triad {t
k
})
db
ds
= n ,
dn
ds
= t + b ,
t
ds
= n (2.79)
Choosing = = 0 we obtain a straight line, r = 1/ and = 0 for a circle
with radius r.
Consider the case of a helix (see gure 2.13) with
r(s) =
_
r cos
_
qs
_
(qr)
2
+ 1
_
, r sin
_
qs
_
(qr)
2
+ 1
_
,
s
_
(qr)
2
+ 1
_
(2.80)
and
(s) =
rq
2
1 + (qr)
2
(2.81)
(s) =
q
1 + (qr)
2
(2.82)
Clearly as r 0 we must approach a straight line. The curvature vanishes indeed
in this limit but the torsion does not.
Prof. Heermann, Heidelberg University
2.1 GENERAL PROPERTIES OF MACROMOLECULES 31
Pitch p
Radius r
Figure 2.13: Denition of the parameters for a helix
We can generalize the Fernet-frame introducing a third parameter
dt
i
(s)
ds
=

j,k

ijk

j
(s)t
k
(s) (2.83)
where

1
= cos ,
2
= sin ,
3
= +
d
ds
(2.84)
This could be used to dene an elastic energy with spontaneous curvature and
torsion {
0k
} (the deviation from equilibrium is denoted by
k
=
k

0k
U =
1
2

k
b
k
_
L
0

2
k
ds (2.85)
The parameters b
k
dene the rigidity. Dening
Prof. Heermann, Heidelberg University
32 MACROMOLECULES
A =
_

_
0
0
0
_

_
(2.86)
with
A
ij
=

ijk

k
(2.87)
we can develop also a numerical procedure to generate curves that have a pre-
scribed spontaneous curvature with uctuations. For this let v
x
= (t
x
1
, t
x
2
, t
x
3
, ) etc.
then we write the equation 2.83 as
dv
i
ds
= Av
i
(2.88)
which can be discretized as
v
i
(s + ds) = Ov
i
(s) (2.89)
with
O = (1 +
ds
2
A)(1
ds
2
A)
1
(2.90)
Note that O is an orthogonal matrix guaranteeing that we consistently generate
orthogonal triads.
In gure is depicted the case for a curve where the spontaneous curvature is set
such that a circle is preferred.
2.1.4 Self-Avoiding Chains
The above models all lack the excluded volume interaction between the monomers.
Indeed, the ubiquitous polymer model is a self-avoiding random walk.
Let U(R
n
R
m
) be a monomer-monomer interaction potential assumed to handle
the excluded volume. We treat the polymer as gas of disconnected monomers
conned within the same volume V as the polymer coil. If

R denotes the average
extent of the chain then the chain occupies a volume V =

R
3
. Let F
c
be the term
that arises from the chemical work done by initially preparing the monomers in
Prof. Heermann, Heidelberg University