additionalmathematicsadditionalmat

hematicsadditionalmathematicsaddit
ionalmathematicsadditionalmathema
ticsadditionalmathematicsadditional
mathematicsadditionalmathematicsa
dditionalmathematicsadditionalmath
ematicsadditionalmathematicsadditi
onalmathematicsadditionalmathemat
icsadditionalmathematicsadditional
mathematicsadditionalmathematicsa
dditionalmathematicsadditionalmath
ematicsadditionalmathematicsadditi
onalmathematicsadditionalmathemat
icsadditionalmathematicsadditional
mathematicsadditionalmathematicsa
dditionalmathematicsadditionalmath
ematicsadditionalmathematicsadditi
onalmathematicsadditionalmathemat
icsadditionalmathematicsadditional
mathematicsadditionalmathematicsa



DIFFERENTIATION


Name

........................................................................................


Differentiation
zefry@sas.edu.my
CHAPTER 9 : DIFFERENTIATION:















































9.1: To determine the limit of a function
- Dont write the substitution.
- If
0
0
or

is found in the solution then the function have to be

-
simplify by factorization.
- Remember that if a
=
0 then
0
a
=

and
a
0
= 0 .
- Example of factorization :
(a) (b)

|
.
|

\
|
+ = +
x
b
a x b ax

|
.
|

\
|
+ = +
x
b
a x bx ax
2 2














EXAMPLE:
Evaluate the following limits.

1.
x
x
x
6
2 lim
3
+

2.
1 2
2
lim
2
2
1
+
+

x x
x x
x
3.
( )x x x
x
o
o
+

1
lim
0


Question Step
Solution/Answer
1. 1. Substitute (without write it down)
the value of x and write the answer.


8

2.

1. Substitute (without write it down)
the value of x and write the answer.

0
0


2. Simplify the function, hence
calculate the limit.





3.

1. Substitute (without write it down)
the value of x and write the answer.


2
1
x


Differentiation
zefry@sas.edu.my


EXERCISE 1:
Evaluate the following limits
1.
2
1
lim
0

x
x
3.
6 5
4
lim
2
2
2
+

x x
x
x
5.
x
x
x
x
2
2
1
lim
|
.
|

\
|
+










2. x x
x
o
o
+

2 lim
0
4.
x x
x
o
o
+

1
lim
0
6. ( ) x x x
x
o
o
+ +

6 3 lim
2
0








9.2: To find
dx
dy
by first principle:


























1. Using
y o
and
x o
.
2. Solving simultaneous equation .
3. Determine the expression for
x
y
o
o
.

4. Using .
x
y
lim
0 x
o
o
o



Differentiation
zefry@sas.edu.my























EXERCISE 1: Find the first derivative of x y 2 5 = by using the first principle.


Step Solution
1. Let the function given be the first equation.

2. Let the equation using x and y o o be the
second equation.



3. Second equation minus first equation and express
y o in terms of . x o



4. Determine .
x
y
o
o


5. Determine
dx
dy
by using . lim
0
x
y
x
o
o
o
















EXAMPLE:
Find the first derivative of 7 4 = x y by using the first principle.

Step Solution
1. Let the function given be the first equation.

7 4 = x y .. (i)

2. Let the equation using x and y o o be the second
equation.

) ( ... 7 ) ( 4 ii x x y y + = + o o


3.Second equation minus first equation and express y o
in terms of . x o

x y o o 4 =
4. Determine .
x
y
o
o

4
5. Determine
dx
dy
by using . lim
0
x
y
x
o
o
o


4


Differentiation
zefry@sas.edu.my



































9.3: Differentiation of a function y = ax
n
, differentiation of a sum and difference of algebraic
functions.
















EXERCISE 2:

Find the first derivative of the following functions using the first
principle.

1. 5 4 + = x y





2. = y
2
2
1
x









3.
x
y
3
2
=

1. Given y = x
n
then
dx
dy
= n x
n 1

2. Given y = ax
n
then
dx
dy
= an x
n 1

3. Given y = k then
dx
dy
= 0 , where k is a constant.
4. Given y = kx then
dx
dy
= k , where k is a constant.
5. If f(x) = p(x) q(x) , then f
/
(x)= p
/
(x) + q
/
(x) where f
/
(x), p
/
(x) and q
/
(x) are first derivatives.
Differentiation
zefry@sas.edu.my
EXAMPLE:
Find
dx
dy
for the following functions :
(a) y = x
4

step solution
1. make sure x is in index form before differentiate x
4

2. differentiate y with respect to x
dx
dy

3. differentiate x
4
with respect to x by Multiply 4 and index Minus 1 4x
3

4. complete answer
dx
dy
= 4x
3


(b) y = x
6

step solution
1. make sure x is in index form before differentiate
2. differentiate y with respect to x


3. differentiate x
4
with respect to x by Multiply 4 and index Minus 1

4. complete answer

































Differentiation
zefry@sas.edu.my

EXERCISE: Find
dx
dy
for the following functions:






















































1 y = x
3


2 y = 5x


3 y = 7

4 y = 6x
2


5 y = 12x

6
y =
25
x
5


7 y = 4x
3
8
y =
x
6



9
y =
4
x
8

10
y =
8
x 4
3

11
y =
( )
2
x 3
2

12
y =
3
x
3
|
.
|

\
|





13 y = 3t x
4
14 y = 400





15
y =
x
7
1

16
y =
2
x 3
1








Differentiation
zefry@sas.edu.my
EXAMPLE 1: Differentiate each of the following functions :
(a) y = 3x
4
+ 2x
3
4

step solution
1. make sure x is in index form before differentiate x
4
, x
3
2. differentiate y with respect to x
dx
dy

3. differentiate all the terms on the right hand side with respect to x 12x
3
+ 6x
2
4. complete answer
dx
dy
=12x
3
+ 6x
2


(b) f(x) =
2
x
3
x
3

step solution
1. make sure x is in index form before differentiate 3x
1
, 3x
2
2. differentiate f(x) with respect to x f
/
(x)

3. differentiate all the terms on the right hand side with respect to x 3x
2
(2)3x
3

4. complete answer
f
/
(x)= 3x
2
(2)3x
3



































Differentiation
zefry@sas.edu.my

























































EXERCISE: Differentiate each of the following functions :
1 y = x
6
3x
3
+ 6 2
y =
9 x 4 x
2
1
2 4
+ +



3
f (x) =
3
x
2
x
2
+

4
f(x) = 1 +
2
x
1
x
1
+






5 y = (x 1) (2x + 5) 6
y =
2
(2 3 ) y x =






7
v =
t
9 t 2
2

8
s =
2
t
) t 3 2 )( 1 t ( +







Differentiation
zefry@sas.edu.my
9.4: Differentiation of a Composite function .







EXAMPLE:
Differentiate y = (2x
3
+ 5)
6
with respect to x:

steps solution
1. recognise the composite
function
k ( ax + b)
n

(2x
3
+ 5)
6


2. differentiate y with respect to x
dx
dy

3. differentiate composite function
|
|
.
|

\
|
|
.
|

\
|

bracket
in function
ate differenti
bracket in
function back copy
kn
1 n

6 (2x
3
+ 5)
5
(6x
2
)
4. complete answer

dx
dy
=6 (2x
3
+ 5)
5
(6x
2
)






























Given y = k ( ax + b)
n

Then
dx
dy
= k n ( ax + b)
n 1
(a)
EXERCISE
Differentiate each of the following functions :
1 y = (4x +7)
3
2 y = (x
3
+ 6)
4




3 y = (6 4x
2
)
3
4
f (x) =
6
3
9 x
3
1
|
.
|

\
|






5 f (x) = (x
2
+ 5x 3 )
4
6
y =
1 x 5
2
+




7
y =
4 x
3
2
+


8
s =
2 4
5
( 2) t






9
v =
3 2
) 6 t 4 t (
1
+






10
y = ( )
2
3
x 3 x 6 5



Differentiation
zefry@sas.edu.my
9.5: Differentiation of the Product of Algebraic functions.








EXAMPLE: Find
dx
dy
for y = (3x
2
2)( x
2
+5x +4).
step solution
1. recognise the product function
v u y=

u = (3x
2
2)

v = ( x
2
+5x +4).
2. differentiate y with respect to x
dx
dy

3. differentiate product function

( )( ) ) u ate differenti ( ) v copy ( v ate differenti u copy +

(3x
2
2) (2x + 5) + ( x
2
+ 5x + 4) (6x )
4. complete answer
dx
dy
= (3x
2
2) (2x +5) + ( x
2
+5x +4) (6x)
5. Simplify the answer
dx
dy
= 12x
3
+ 45x
2
+ 20x 10
Exercise : Find
dy
dx

1. y = 2x
3
( 2 x
5
) 2. y = (4x +7) (3x
2
5)

y = (x
3
+ 6)

(1 4x +2x
2
)





3. y = (x
3
+ 6)

(1 4x +2x
2
) 4. y = x
2
(x + 1)
4







5. y = x
2
(4-3x )
2
6. y = (2x + 1) (x + 3)
3










Method The Product Rule
If v u y= , then find the first derivative of u and v.
Then substitute into the formula:
dx
du
v
dx
dv
u
dx
dy
+ =

Differentiation
zefry@sas.edu.my
9.6: Differentiation of the Quotient of Algebraic functions.












EXAMPLE:





Steps solutions

1.


Determine whether product or quotient
function involved .

y =
v
u
quotient function.


2.
Use the quotient rule for , y =
v
u

2
v
dx
dv
u
dx
du
v
dx
dy

=

3.

Determine u and v , and find
dx
du
and
dx
dv

by differentiating
u and v with respect to x .


u = x
3
, v = 2 x
4

2
3x
dx
du
=
3
4x
dx
dv
=

4.




Substitute into the formula.


( )( ) ( )
( )
2
4
3 3 2 4
2
4 3 2
x
x x x x
dx
dy

=

5 Simplify your answer.


( )
2
4
6 6 2
2
4 3 6
x
x x x
dx
dy

+
=
( )
2
4
6 2
2
6
x
x x
dx
dy

+
=










Method The Quotient Rule
If
( )
( ) x v
x u
y =
, then find the first derivative of u and v.
Then substitute into the formula:
2
v
dx
dv
u
dx
du
v
dx
dy

=

Given that
4
3
2 x
x
y

=
, find
dx
dy
. Guide: Dont expand the denominator





Differentiation
zefry@sas.edu.my
EXERCISE:

1. y =
2
2
x
x

2. y =
3 x
x 5
+













3. y =
2
2
3
7
x
x

4. y =
1 x
) x 3 (
2
+

5. f (x) =
3
) 1 x (
5 x 2
+
+

6. f (x) =
2 x 5
) x 3 1 (
4
+

Differentiation
zefry@sas.edu.my
9.7: GRADIENT OF TANGENT AND NORMAL















EXAMPLE:.
Given that P( 1 , 4 ) is a point on a curve y = 6 + 5x -7x
2

Find
(a) the gradient of tangent and the gradient of normal at point P.

(b) the equation of tangent and the equation of normal at point P.



































1. Determine the gradient of tangent at a point by substitution the x-
coordinate into
dx
dy
.

2. Determine the gradient of normal by referring to the gradient of the
tangent.

3. Determine the equation of tangent and normal at a point of a curve by
using the formula
) (
1 1
x x m y y =
Steps Solution
1. Find .
dx
dy


x 14 5
dx
dy
=

2. Find the gradient of tangent by Substitution the value of x.
9 ) 1 ( 14 5
dx
dy
= =
3. Find the gradient of normal by
using formula.
m
1
m
2
= 1
9
1
m
normal
=
4. Find the equation of tangent.
y y
1
= m
1
(x x
1
)
y = - 9x + 13
5. Find the equation of normal.
y y
1
= m
2
(x x
1
)

4
15
x
9
1
y + =



Differentiation
zefry@sas.edu.my
























































EXERCISE

1. Given that P(1,7) is a point on curve y = 3x
2
x + 5 . Find
(a) the gradient of tangent and the gradient of normal at point P.
(b) the equation of tangent and the equation of normal at point P

















2. Given that P(2,4) is a point on curve y = (2x 3)(x + 2) .
Find
(a) the gradient of tangent and the gradient of normal at point P.
(b) the equation of tangent and the equation of normal at point P.















Differentiation
zefry@sas.edu.my
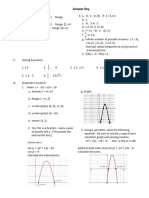
9.8: TURNING POINTS - MINIMUM OR MAXIMUM.
























































EXAMPLE: Find the turning point of the curve y = 3x
2
x
3
+ 5 and determine its maximum and
minimum point.
Step Solution
1. To determine the turning point
i Find
dx
dy
.
i) y = ax
n
ii) y = kx

dx
dy
= a
1 n
nx
dx
dy
= k

dx
dy
= 6x 3x
2


ii. Let
dx
dy
= 0 .
and solve for x .
6x 3x
2
= 0
3x(2 x) = 0
x = 0 , x = 2
iii. To determine the y-coordinate for each value of
x that satisfy the above equation .

y = 0 0 + 5 = 5
y = 3(2)
2
- 2
3
+ 5 = 9
iv. State the turning point (0, 5) and (2, 9)
2. To determine the maximum or minimum
point
i. Find
2
2
dx
y d




2
2
dx
y d
= 6 6x
ii. Substitute the value of x to get the value of
2
2
dx
y d
x = 0,
2
2
dx
y d
= 6 0 = 6
2
2
dx
y d
> 0 min
x = 2,
2
2
dx
y d
=6-6(2) = -6 < 0 max
iii. State the coordinate
Minimum point (0. 5)
Maximum point (2, 9)


1. To find the turning points
- Find
dx
dy
.
- Lets
dx
dy
= 0 , solve the equation to find x.
- Find the value of y.
- State in ordered pairs (x,y) .
2. To determine whether the turning point is a
maximum or minimum point.
- Find
2
2
dx
y d
.
- Substitute the value of x to the product of the differentiation .
- If
2
2
dx
y d
< 0, maximum point.
If
2
2
dx
y d
> 0, minimum point.
3. The difference between maximum/minimum point with
the maximum/minimum value
- Point : in ordered pairs ( x, y)
- Value : refers only to the value of y.
Differentiation
zefry@sas.edu.my
EXERCISE

Find (a) the turning point (b) determine the maximum or minimum point (c) max/min value , from
the following curve equations.
1. y = x
2
+2x

+ 3

2. y = 4 + 8x -x
2
















3. y = 2x
3
+6x
2
-1 4. y = x
3
-12x +1




































Differentiation
zefry@sas.edu.my
9.9 Rate of change

,

y
area
volume
dy
differentiate y with respect to x
dx
dx
rate of change of x
dt
dy
rate of change of
dt
dA
rate of change of
dt
dV
rate of change of
dt
=
=
=
=
=


Formulae frequently used:

.
.
.
dy dy dx
dt dx dt
dA dA dr
dt dr dt
dV dV dr
dt dr dt
=
=
=


EXAMPLE: Given y=x
2
+ 4x +3 and the rate of change of x is 0.5 unit s
-1
when x= 2, find the rate of
change of y.
Step Solution
1. Using formula
.
dy dy dx
dt dx dt
=
2. Given
0.5

dx
dt
dy
find
dx
=

2 4
2, 2(2) 4 8
dy
x
dx
dy
x
dx
= +
= = + =

3. Substitute into formula 1
.
dy dy dx
dt dx dt
=
= 8(0.5) =4














Differentiation
zefry@sas.edu.my
Exercise

1.Given y=x
2
- 6x +2 and x decreases at the rate
of 0.5 unit s
-1
when x= 3, find the rate of change
of y.

2. Given y=x
3
- 4x +5 and x increases at the rate
of 2 unit s
-1
when x= 4, find the rate of change of
y.














4. The radius of a circle increases at the
rate of 2 cms
-1
when its radius is 10
cm. Find the rate of change in its area
5. The radius of a sphere decreases at
the rate of 2 cms
-1
when its radius is 8
cm. Find the rate of change in its
volume


























Differentiation
zefry@sas.edu.my

9.10: Small change And Approximation.






















































- The increment in y, x
dx
dy
y o o ~
ox = the small change in x

- If x is decreasing then ox is negative .

- The differences between the small change of y with the
approximate value of y
- The small change of y is oy
- The approximate value of y = y
origin
+ oy
y
origin
= the value of y before x changes
EXAMPLE: Given that y = x
2
+ 5x, use differentiation to find the small change in y
when x increases from 3 to 3.01.
Step Solution
Keyword
- find oy



1. Using formula




2. Determine the
- Value of x

- Value of ox

- Find
dx
dy

- substitute the value of x



3. Substitute into the formula (1)









Differentiation
zefry@sas.edu.my


1. Given that y = 2x
3
+6x
2
, find the small
change of y when x increase from 2 to 2.01
3. Find the approximate increase in the area of a
circle when its radius increases from 5 to 5.03














2. Given that y = 6t + t, find the small change
of y when t increase from 2 to 2.01.

4. The radius of a cylinder is fixed at 4 cm. If the
height of the cylinder decreases by 0.25, find
the approximate decrease in the volume of the
cylinder.