Hyperbolic function

1
Hyperbolic function
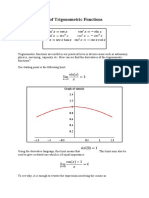
A ray through the origin intercepts the unit hyperbola in the point
, where is twice the area between the ray, the hyperbola, and
the -axis. For points on the hyperbola below the -axis, the area is considered
negative (see animated version with comparison with the trigonometric (circular)
functions).
In mathematics, hyperbolic functions are
analogs of the ordinary trigonometric, or
circular, functions. The basic hyperbolic
functions are the hyperbolic sine "sinh"
(/snt/ or /an/), and the hyperbolic cosine
"cosh" /k/, from which are derived the
hyperbolic tangent "tanh" (/tnt/ or
/n/), hyperbolic cosecant "csch" or
"cosech" /kok/ or /kost/, hyperbolic
secant "sech" /k/ or /st/, and
hyperbolic cotangent "coth" /ko/ or
/k/,
[1]
corresponding to the derived
trigonometric functions. The inverse
hyperbolic functions are the area hyperbolic
sine "arsinh" (also called "asinh" or
sometimes "arcsinh")
[2]
and so on.
Just as the points (cost,sint) form a circle
with a unit radius, the points (cosht,sinht)
form the right half of the equilateral
hyperbola. Hyperbolic functions occur in the
solutions of some important linear differential equations, for example the equation defining a catenary, of some
cubic equations, and of Laplace's equation in Cartesian coordinates. The latter is important in many areas of physics,
including electromagnetic theory, heat transfer, fluid dynamics, and special relativity.
The hyperbolic functions take real values for a real argument called a hyperbolic angle. The size of a hyperbolic
angle is the area of its hyperbolic sector. The hyperbolic functions may be defined in terms of the legs of a right
triangle covering this sector.
In complex analysis, the hyperbolic functions arise as the imaginary parts of sine and cosine. When considered
defined by a complex variable, the hyperbolic functions are rational functions of exponentials, and are hence
meromorphic.
Hyperbolic functions were introduced in the 1760s independently by Vincenzo Riccati and Johann Heinrich
Lambert.
[3]
Riccati used Sc. and Cc. ([co]sinus circulare) to refer to circular functions and Sh. and Ch. ([co]sinus
hyperbolico) to refer to hyperbolic functions. Lambert adopted the names but altered the abbreviations to what they
are today.
[4]
The abbreviations sh and ch are still used in some other languages, like European French and Russian.
Hyperbolic function
2
Standard algebraic expressions
sinh, cosh and tanh
csch, sech and coth
(a) cosh(x) is the average of e
x
and e
x
(b) sinh(x) is half the difference of e
x
and e
x
Hyperbolic functions (a) cosh and (b) sinh obtained using exponential functions and
The hyperbolic functions are:
Hyperbolic sine:
Hyperbolic cosine:
Hyperbolic tangent:
Hyperbolic cotangent:
Hyperbolic function
3
Hyperbolic secant:
Hyperbolic cosecant:
Hyperbolic functions can be introduced via imaginary circular angles:
Hyperbolic sine:
Hyperbolic cosine:
Hyperbolic tangent:
Hyperbolic cotangent:
Hyperbolic secant:
Hyperbolic cosecant:
where i is the imaginary unit defined by i
2
= 1.
The complex forms in the definitions above derive from Euler's formula.
Useful relations
Odd and even functions:
Hence:
It can be seen that cosh x and sech x are even functions; the others are odd functions.
Hyperbolic sine and cosine satisfy the identity
Hyperbolic function
4
which is similar to the Pythagorean trigonometric identity. One also has
for the other functions.
The hyperbolic tangent is the solution to the nonlinear boundary value problem:
It can be shown that the area under the curve of cosh(x) is always equal to the arc length:
[5]
Sums of arguments:
particularly
Sum and difference of cosh and sinh:
Inverse functions as logarithms
Hyperbolic function
5
Derivatives
Standard integrals
For a full list of integrals of hyperbolic functions, see list of integrals of hyperbolic functions.
Hyperbolic function
6
where C is the constant of integration.
Taylor series expressions
It is possible to express the above functions as Taylor series:
The function sinhx has a Taylor series expression with only odd exponents for x. Thus it is an odd function, that is,
sinhx=sinh(x), and sinh0=0.
The function coshx has a Taylor series expression with only even exponents for x. Thus it is an even function, that
is, symmetric with respect to the y-axis. The sum of the sinh and cosh series is the infinite series expression of the
exponential function.
where
is the nth Bernoulli number
is the nth Euler number
Hyperbolic function
7
Comparison with circular functions
Circle and hyperbola tangent at (1,1) display geometry of circular
functions in terms of circular sector area u and hyperbolic functions
depending on hyperbolic sector area u.
The hyperbolic functions represent an expansion of
trigonometry beyond the circular functions. Both types
depend on an argument, either circular angle or
hyperbolic angle.
Since the area of a circular sector is it will be
equal to u when r = square root of 2. In the diagram
such a circle is tangent to the hyperbola x y = 1 at (1,1).
The yellow sector depicts an area and angle magnitude.
Similarly, the red augmentation depicts an area and
magnitude as hyperbolic angle.
The legs of the two right triangles with hypotenuse on
the ray defining the angles are of length 2 times the
circular and hyperbolic functions.
Identities
The hyperbolic functions satisfy many identities, all of them similar in form to the trigonometric identities. In fact,
Osborn's rule
[6]
states that one can convert any trigonometric identity into a hyperbolic identity by expanding it
completely in terms of integral powers of sines and cosines, changing sine to sinh and cosine to cosh, and switching
the sign of every term which contains a product of 2, 6, 10, 14, ... sinhs. This yields for example the addition
theorems
the "double argument formulas"
and the "half-argument formulas"
[7]
Note: This is equivalent to its circular counterpart multiplied by 1.
Note: This corresponds to its circular counterpart.
Hyperbolic function
8
The derivative of sinhx is coshx and the derivative of coshx is sinhx; this is similar to trigonometric functions,
albeit the sign is different (i.e., the derivative of cosx is sinx).
The Gudermannian function gives a direct relationship between the circular functions and the hyperbolic ones that
does not involve complex numbers.
The graph of the function acosh(x/a) is the catenary, the curve formed by a uniform flexible chain hanging freely
between two fixed points under uniform gravity.
Relationship to the exponential function
From the definitions of the hyperbolic sine and cosine, we can derive the following identities:
and
These expressions are analogous to the expressions for sine and cosine, based on Euler's formula, as sums of
complex exponentials.
Hyperbolic functions for complex numbers
Since the exponential function can be defined for any complex argument, we can extend the definitions of the
hyperbolic functions also to complex arguments. The functions sinhz and coshz are then holomorphic.
Relationships to ordinary trigonometric functions are given by Euler's formula for complex numbers:
so:
Thus, hyperbolic functions are periodic with respect to the imaginary component, with period ( for
hyperbolic tangent and cotangent).
Hyperbolic function
9
Hyperbolic functions in the complex plane
References
[1] tanh (http:/ / www. mathcentre.ac. uk/ resources/ workbooks/ mathcentre/ hyperbolicfunctions. pdf)
[2] Some examples of using arcsinh (http:/ / www. google. com/ books?q=arcsinh+ -library) found in Google Books.
[3] Robert E. Bradley, Lawrence A. D'Antonio, Charles Edward Sandifer. Euler at 300: an appreciation. Mathematical Association of America,
2007. Page 100.
[4] Georg F. Becker. Hyperbolic functions. Read Books, 1931. Page xlviii.
[5] , Extract of page 472 (http:/ / books.google.com/ books?id=hfi2bn2Ly4cC& pg=PA472)
[6] G. Osborn, Mnemonic for hyperbolic formulae (http:/ / links. jstor. org/ sici?sici=0025-5572(190207)2:2:34<189:1MFHF>2. 0. CO;2-Z), The
Mathematical Gazette, p. 189, volume 2, issue 34, July 1902
[7] , Chapter 26, page 1155 (http:/ / books. google. com/ books?id=PGuSDjHvircC& pg=PA1155)
External links
Hazewinkel, Michiel, ed. (2001), "Hyperbolic functions" (http:/ / www. encyclopediaofmath. org/ index.
php?title=p/ h048250), Encyclopedia of Mathematics, Springer, ISBN978-1-55608-010-4
Hyperbolic functions (http:/ / planetmath. org/ encyclopedia/ HyperbolicFunctions. html) on PlanetMath
Hyperbolic functions (http:/ / mathworld. wolfram. com/ HyperbolicFunctions. html) entry at MathWorld
GonioLab (http:/ / glab. trixon. se/ ): Visualization of the unit circle, trigonometric and hyperbolic functions (Java
Web Start)
Web-based calculator of hyperbolic functions (http:/ / www. calctool. org/ CALC/ math/ trigonometry/
hyperbolic)
Article Sources and Contributors
10
Article Sources and Contributors
Hyperbolic function Source: http://en.wikipedia.org/w/index.php?oldid=604474202 Contributors: A876, Aaron Rotenberg, Access Denied, Agro r, AlanUS, Albmont, Alle, Allispaul,
AndrewWTaylor, Andy Fisher aKa Shine, Armeria wiki, Ashis Kumar Sahoo, AxelBoldt, Azo bob, Barak Sh, Bcherkas, Ben pcc, BenFrantzDale, Bh3u4m, Bhadani, Blah314, Brad7777,
Brighterorange, Calvinballing, Can't sleep, clown will eat me, Canderson7, Carlodn6, Charles Matthews, Chris-gore, ChrisGualtieri, Chzz, CiaPan, Coasterlover1994, Cojoco, Compotatoj,
Cottonmouse, Courcelles, Ctifumdope, Culero101, Cyp, DVdm, Daniele Pugliesi, Dcqec111, Deathbeast, Deflective, Derepi, Deskana, Dlituiev, Doctormatt, Double sharp, Dr Greg, Dragnmn,
Drilnoth, Duoduoduo, Eettttt, Egmontaz, Eleolar, Email4mobile, Eric119, Error792, Evil saltine, Fanix1128, Faramir1138, Footyfanatic3000, Fredrik, Gabbe, Gauge, Gco, GeiwTeol, Gene Ward
Smith, Georg Muntingh, Georgia guy, Geraldshields11, Gesslein, Giftlite, Goffrie, Gogo Dodo, Googl, Guardian of Light, Hashar, Hdt83, Heliomance, Herbee, HowiAuckland, Husond, Icairns,
IgnorantArmies, JP.Martin-Flatin, Jackfork, Jdh8, Jeandavid54, Jleedev, JoeHillen, John of Reading, Josh Grosse, Jrgsampaio, Justin W Smith, K4vin, KarlJorgensen, KennethJ, Kiensvay,
KnowledgeOfSelf, Krishnavedala, Kritikool99, Ktims, Kwamikagami, LOL, Lambiam, Lee, Linas, LokiClock, LucasVB, Lzur, Macrakis, MadGuy7023, Maksim-e, MarSch, MarkSweep,
Mate2code, Materialscientist, Matt24, Me and, Mebden, Metacomet, Michael Hardy, Michael.YX.Wu, Michiganfan9000, Mleconte, Montparnasse, Moverington, Moxfyre, N4m3, Nascar1996,
Nbarth, Ninly, Noerdosnum, Nonagonal Spider, Oleg Alexandrov, PAR, Patchouli, Pikalax, Pne, Pokajanje, Policron, Prophile, Qantas94Heavy, Qwertyus, Reciprocist, Rgdboer, Richnfg,
Roberdin, Rocketrod1960, Rocky2009, SKvalen, Salih, Sam Derbyshire, Scientific29, SebastianHelm, Seraph85, Sergiacid, Sharonlees, Shen, Shubham10,000, Silly rabbit, Sjakkalle, Smack,
Snevets, Societelibre, Sohale, Steve911411, Suisui, Sverdrup, Swetrix, TV4Fun, TYelliot, TakuyaMurata, The Anome, TheBendster, Tim bates, Tob, Tobias Bergemann, Tsemii, Txebixev,
Urhixidur, V1adis1av, Vinograd19, Vizziee, Vt Zajac, WIKIWIZDOM, Wagnerjp25, Wavelength, Wereon, Wiccan Quagga, WikHead, WojciechSwiderski, Wwoods, Xanthoxyl, Zvika, 413
anonymous edits
Image Sources, Licenses and Contributors
Image:Hyperbolic functions-2.svg Source: http://en.wikipedia.org/w/index.php?title=File:Hyperbolic_functions-2.svg License: Public Domain Contributors: Hyperbolic_functions.svg:
Original uploader was Marco Polo at en.wikipedia derivative work: Jeandavid54 (talk)
Image:sinh cosh tanh.svg Source: http://en.wikipedia.org/w/index.php?title=File:Sinh_cosh_tanh.svg License: Public Domain Contributors: Original uploader was Ktims at en.wikipedia
Image:csch sech coth.svg Source: http://en.wikipedia.org/w/index.php?title=File:Csch_sech_coth.svg License: Public Domain Contributors: Original uploader was Ktims at en.wikipedia
file:Hyperbolic and exponential; cosh.svg Source: http://en.wikipedia.org/w/index.php?title=File:Hyperbolic_and_exponential;_cosh.svg License: Creative Commons Attribution-Sharealike
3.0 Contributors: Krishnavedala
file:Hyperbolic and exponential; sinh.svg Source: http://en.wikipedia.org/w/index.php?title=File:Hyperbolic_and_exponential;_sinh.svg License: Creative Commons Attribution-Sharealike
3.0 Contributors: Krishnavedala
File:Circular and hyperbolic angle.svg Source: http://en.wikipedia.org/w/index.php?title=File:Circular_and_hyperbolic_angle.svg License: Creative Commons Zero Contributors:
User:Maschen
Image:Complex Sinh.jpg Source: http://en.wikipedia.org/w/index.php?title=File:Complex_Sinh.jpg License: Public Domain Contributors: Jan Homann
Image:Complex Cosh.jpg Source: http://en.wikipedia.org/w/index.php?title=File:Complex_Cosh.jpg License: Public Domain Contributors: Jan Homann
Image:Complex Tanh.jpg Source: http://en.wikipedia.org/w/index.php?title=File:Complex_Tanh.jpg License: Public Domain Contributors: Jan Homann
Image:Complex Coth.jpg Source: http://en.wikipedia.org/w/index.php?title=File:Complex_Coth.jpg License: Public Domain Contributors: Jan Homann
Image:Complex Sech.jpg Source: http://en.wikipedia.org/w/index.php?title=File:Complex_Sech.jpg License: Public Domain Contributors: Jan Homann
Image:Complex Csch.jpg Source: http://en.wikipedia.org/w/index.php?title=File:Complex_Csch.jpg License: Public Domain Contributors: Jan Homann
License
Creative Commons Attribution-Share Alike 3.0
//creativecommons.org/licenses/by-sa/3.0/