Formal and Informal Proof on How to Find the Solutions of a Quadratic

Lets begin this journey by analyzing what a quadratic function is and its appearance
graphically. Suppose that if you throw a ball, it will go up, and it will slow down as it
reaches its maximum height, then the ball comes down. If the acceleration of the
ball is a constant, then for position vs. time you will get a quadratic function. The
quadratic formula is used to find the roots of a quadratic equation. The roots are the
x-values of the points where the graph intersects the x-axis.
Informal
Figure 1 represents a quadratic equation in its standard form.
Figure 1: Standard Form of Quadratic Equation

The letters a, b, and c are constants, where (a 0), and x is the variable.
There are two forms of the quadratic equation. One of them is the standards form,
which is described above. The other one is the vertex form.
The vertex form is() ( )

, where (h, k) represent the vertex. If a is

negative then the parabola opens Downwards. If a is positive, then the parabola
opens upwards. If the absolute value of a is less than one, then the parabola
widens. If the absolute value is greater than one, then the parabola becomes
narrower. When you have a quadratic equation you can find the discriminant. The
discriminant is a number calculated from the quadratic equation, it provides critical
information about the solutions. The discriminant can be found using

. If
the value of,

is positive, then there are two real solutions. If it equals zero

the equation only one unique real solution. If the discriminant is negative then there
are no real solutions, but two imaginary solutions. Now that you have more
knowledge about quadratics, I can proceed to the next step.














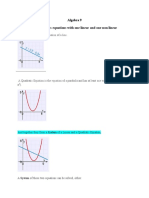
A graph of a quadratic equation is represented above. This graph shows that the
leading coefficient of the quadratic equation has to be positive. The axis of
symmetry is the x-value of the vertex, the vertex, in this example, is (2,-4). If the
graph opens downward, the leading coefficient is negative, and the vertex would be
the maximum point on the graph.










The graph above has complex solutions. When a graph does not intersect the x-axis,
then the discriminant is negative. When the discriminant is negative then the roots
to the equation are complex conjugates. To find the solutions of the graph above the
most appropriate thing to do is to use the quadratic formula.







The graph above only have one unique real solution. This is when the discriminant
is equal to zero. The graph above has two real solutions, but it only has one unique
solution, this is because the equation has a multiplicity of two. To find the root of
this solution of this equation, one can look at the vertex or at the minimum point on
the graph.


To find the solutions, roots, or zeros of a quadratic equation you can start by looking
at a graph. Given a quadratic function y =

, then you have the following
graph.








If the equation has two real solutions you can find the solutions by figuring out
where the graph touches the x-axis. Where the graph intersects the x-axis, the y
value is zero. To show that your findings are correct, you can use the points to find
the midpoint. If the midpoint x-value is the same as the axis of symmetry, then you
have done the correct work.


Formal
The solutions to a quadratic equation can be found by using the quadratic formula.
The quadratic formula is the following,

, this formula contains the

axis of symmetry (

) and the formula to find the discriminants (

)
The quadratic formula can be derived from the standard equation of a quadratic.
The method used to derive this formula is, completing the square. The following
steps are the steps you will need to take in order to derive the quadratic formula
from the standard equation of a quadratic.

Divide by a, because the coefficient of X

2

has to be one.

I subtracted

from both sides, because I want to isolate the

variables from constants. Now complete the square.
To complete the square, you need to take the coefficient of x and divided by two,
once you divide it by two you squared.

I divided the coefficient of x by two.

Once I divided the coefficient of x by two, I squared.

Since I divided by (

I have to subtract by (

because I want to add zero to the equation and not make changes.

Now add (

to both sides.

Now factor the left side

(

Now find a common denominator for the right side

(

Use the commutative property for addition, rearrange -4ac

and b
2
(

Now take the square root, remember that, every time you
take the square root of something there are two solutions.

Simplify

Now subtract

from both sides

Since there is a common denominator you can combine the

subtraction.

This is the Quadratic Formula.

The Quadratic Formula contains the expression for the line of symmetry. It
appears as part of the formula as

The line of symmetry basically represents the

midpoint between the two solutions.
As I have demonstrated the solutions to a quadratic equation can be found in
two different ways. The first is visually. You can find the solution by looking at the
equations graph and finding where the graph touches the x-axis. The second method
is to use the quadratic equation. The quadratic formula may be used to find real or
imaginary solutions for any quadratic equation. In conclusion, finding solutions
using the quadratic formula may be useful and efficient as shown throughout this
document.





















References
"Quadratic Graph Information - MathBitsNotebook(A1 - CCSS Math)."Quadratic Graph
Information - MathBitsNotebook(A1 - CCSS Math). N.p., n.d. Web. 04 May 2014.