Professional Documents
Culture Documents
Week 3 Lect 3
Uploaded by
BobOriginal Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Week 3 Lect 3
Uploaded by
BobCopyright:
Available Formats
MATH2831/2931
Linear Models/ Higher Linear Models.
August 14, 2013
Week 3 Lecture 3 - Last lecture:
Least squares estimation of parameters in the general linear
model.
The full rank linear model.
Example - Polynomial regression
Example 2 - Basis Function Regressions
Week 3 Lecture 2 - This lecture:
Properties of least squares estimator of .
Week 3 Lecture 2 - Formulation of the general linear model
Responses y
1
, ..., y
n
.
The general linear model:
y
i
=
0
+
1
x
i 1
+ ... +
k
x
ik
+
i
where
0
, ...,
k
are unknown parameters and
i
, i = 1, ..., n are a
collection of uncorrelated errors with zero mean and common
variance
2
.
_
_
y
1
.
.
.
y
n
_
_
=
_
_
1 x
11
. . . x
1k
.
.
.
.
.
.
1 x
n1
. . . x
nk
_
_
_
0
.
.
.
k
_
_
+
_
1
.
.
.
n
_
_
or
y = X + .
Week 3 Lecture 2 - Full rank linear model
Least squares estimate b of (provided (X
X)
1
exists) is
b = (X
X)
1
X
y.
For simple linear regression model, we derived expressions for:
E(b
0
), E(b
1
), Var (b
0
), Var (b
1
), Cov(b
0
, b
1
).
For least squares estimator b of , want similar results.
Expectations of random vectors.
Y = (Y
1
, ..., Y
k
)
a random vector, E(Y
i
) =
i
, then
E(Y) = = (
1
, ...,
n
)
.
Week 3 Lecture 2 - Result about vector expectations
Lemma:
i) If a is a k 1 vector of constants then E(a) = a.
ii) If a is a k 1 vector of constants, and Y is a k 1 random
vector with E(Y) = , then E(a
Y) = a
.
iii) If A is an n k matrix, and Y is a k 1 random vector with
E(Y) = , then E(AY) = A.
Week 3 Lecture 2 - Vector expectations
Proof of i) is obvious.
Proof of ii:
a
Y =
k
i =1
a
i
Y
i
and hence
E(a
Y) = E(
k
i =1
a
i
Y
i
)
=
k
i =1
a
i
E(Y
i
)
=
k
i =1
a
i
i
= a
Week 3 Lecture 2 - Vector expectations
Proof of iii:
(AY)
i
=
k
m=1
A
im
Y
m
and so
E((AY)
i
) = E(
k
m=1
A
im
Y
m
)
=
k
m=1
A
im
E(Y
m
)
=
k
m=1
A
im
m
= (A)
i
.
Week 3 Lecture 2 - Unbiasedness of b
Exercise: apply the lemma just proved to show that b, the least
squares estimator of , is unbiased.
We have
b = (X
X)
1
X
y,
so, applying our lemma
E(b) = (X
X)
1
X
E(y)
= (X
X)
1
X
X
=
so that the least squares estimator is unbiased.
We would also like some measure of the precision of b.
What are the variances of components of b? Covariances?
Week 3 Lecture 2 - Covariance matrices
Covariance matrix (sometimes called variance-covariance matrix)
of a random vector:
Y is a k 1 random vector, the covariance matrix of Y denoted
Var (Y), k k matrix with element (i , j ) equal to Cov(Y
i
, Y
j
).
We have seen that expected value of a random matrix A is the
matrix with the same dimensions as A and with element (i , j )
equal to E(A
ij
).
Hence, we can write:
Var (Y) = E((Y )(Y )
)
Diagonal elements of Var (Y) are variances of components of Y,
and Var (Y) is symmetric (since Cov(Y
i
, Y
j
) = Cov(Y
j
, Y
i
)).
Week 3 Lecture 2 - Results about variances and covariance
matrices
Lemma:
i) Let Y be a k 1 random vector with Var (Y) = V. If a is a
k 1 vector of real numbers, then
Var (a
Y) = a
Va.
ii) Let Y be a k 1 random vector with Var (Y) = V. Let A be a
k k matrix. If Z = AY, then
Var (Z) = AVA
.
Week 3 Lecture 2 - Covariance matrices
Proof of i:
Var (a
Y) = Var (
k
i =1
a
i
Y
i
) = E
_
_
_
k
i =1
a
i
Y
i
k
i =1
a
i
i
_
2
_
_
= E
_
_
_
k
i =1
a
i
(Y
i
i
)
_
2
_
_
= E
_
_
k
i =1
k
j =1
a
i
a
j
(Y
i
i
)(Y
j
j
)
_
_
=
k
i =1
k
j =1
a
i
a
j
E((Y
i
i
)(Y
j
j
))
=
k
i =1
k
j =1
a
i
a
j
V
ij
= a
Va.
Week 3 Lecture 2 - Covariance matrices
Cov(Z
i
, Z
j
) = Cov
q=1
A
iq
Y
q
,
k
r =1
A
jr
Y
r
= E
q=1
A
iq
(Y
q
q
)
r =1
A
jr
(Y
r
r
)
= E
q=1
k
r =1
A
iq
A
jr
(Y
r
r
)(Y
q
q
)
=
k
q=1
k
r =1
A
iq
A
jr
V
qr
=
k
q=1
A
iq
k
r =1
V
qr
A
jr
=
k
q=1
A
iq
(VA
)
qj
= (AVA
)
ij
Week 3 Lecture 2 - Properties of least squares estimator
Theorem:
In the full rank linear model, the least squares estimator
b = (X
X)
1
X
y is unbiased,
E(b) =
with covariance matrix
Var (b) =
2
(X
X)
1
.
Week 3 Lecture 2 - Properties of least squares estimator
Recall:
E(b) = E((X
X)
1
X
y)
= (X
X)
1
X
X
=
Finding an expression for the covariance matrix is easy to do using
the previous lemma.
Using Var (y) =
2
I (where I is the identity matrix)
Var (b) =
2
(X
X)
1
X
((X
X)
1
X
=
2
(X
X)
1
X
X(X
X)
1
=
2
(X
X)
1
Week 2 Lecture 2 - Polynomial Regression (Special
examples of LINEAR MODELS).
In a polynomial regression model we consider multiple
predictors which can be used to construct a model such as the
examples:
y
i
=
0
+
J
j =1
j
x
ij
+
K
k=1
L
l =1
kl
x
l
ik
+
M
m=1
S
s=1
ms
x
im
x
is
+ . . . +
i
For example we could consider:
y
i
=
0
+
1
x
4
i 1
+
2
x
i 3
+
3
x
i 1
x
i 4
+
i
HOW DO WE SELECT SUCH MODELS?
ARE THERE STATISTICAL PROCEDURES?
ARE THEY AUTOMATED PROCEDURES ?
Week 3 - Basis Function Regression.
Enough of basic regression what else can we do? (note small
change to notation here)
Now consider an extension to the class of linear models so far
considered:
y = f (x, w) +
where
f (x, w) = w
0
+
M1
j =1
w
j
j
(x) = w
T
(x)
with
j
(x) a basis function and we dene
0
(x) = 1.
We still typically assume zero mean Gaussian errors
N(0, ) ( =
2
).
Basis regression is important to many areas of applied
statistics, Signal Processing Engineering, nancial modelling,
spatial point process modelling ....
Week 3 - Basis Function Regression.
Some Popular Basis Functions:
Many choices can be used:
Gaussian basis:
j
(x) = exp
_
(x)
2
2s
2
_
Sigmoidal basis:
j
(x) =
_
x
s
_
where the logistic sigmoid
function (a) =
1
1+exp(a)
or (a) =
tanh(a)+1
2
.
1 0 1
1
0.5
0
0.5
1
1 0 1
0
0.25
0.5
0.75
1
1 0 1
0
0.25
0.5
0.75
1
Figure : polynomial basis functions, Gaussian basis functions and
sigmoidal basis function examples.
Week 3 - Basis Function Regression.
Hence our model is now:
p(y|x, w, ) = N(y|f (x, w), ).
Under the squared error loss function (we know from week
one simple linear model case) that the optimal prediction, for
a new value of x is given by the the conditional mean of the
target variable -
E(y|x) =
_
yp(y|x)dy = f (x, w).
Our least squares estimates carry through in the same manner
as before =
_
_
1
T
y
Week 3 - Basis Function Regression.
Where the design matrix for the basis function regression becomes
=
_
0
(x)
1
(x) . . .
M
(x)
=
_
0
(x
11
)
1
(x
11
) . . .
M
(x
1M
)
.
.
.
.
.
.
0
(x
11
)
1
(x
1n
) . . .
M
(x
nM
)
_
_
Week 2 Lecture 2 - Learning Expectations.
Be familiar with the matrix formulation of the linear regression
model.
Be able to apply basic matrix manipulations to obtain the
least squares estimate and its mean and variance.
You might also like
- 01 7.1 Distributions 13-14-0 PDF Week 7 New VersionDocument21 pages01 7.1 Distributions 13-14-0 PDF Week 7 New VersionBobNo ratings yet
- 10 FM 1 TN 1ppDocument101 pages10 FM 1 TN 1ppBobNo ratings yet
- Calc 1141 2Document27 pagesCalc 1141 2BobNo ratings yet
- 01 7.1 Distributions 13-14Document33 pages01 7.1 Distributions 13-14BobNo ratings yet
- ch19 3Document40 pagesch19 3BobNo ratings yet
- ch19 5Document6 pagesch19 5BobNo ratings yet
- ACTL4001 Lecture 11Document12 pagesACTL4001 Lecture 11BobNo ratings yet
- (Carmona R.a.) Interest Rate ModelsDocument58 pages(Carmona R.a.) Interest Rate ModelsBobNo ratings yet
- The Global Financial Crisis: - An Actuarial PerspectiveDocument3 pagesThe Global Financial Crisis: - An Actuarial PerspectiveBobNo ratings yet
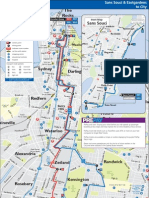
- 301 302 303 X03mapDocument1 page301 302 303 X03mapKyungJun ShinNo ratings yet
- Linear Algebra Done WrongDocument231 pagesLinear Algebra Done WrongS NandaNo ratings yet
- 376 - 377 Bus MapDocument1 page376 - 377 Bus MapBobNo ratings yet
- History of The Actuarial ProfessionDocument3 pagesHistory of The Actuarial ProfessionBobNo ratings yet
- Linear Algebra Done WrongDocument231 pagesLinear Algebra Done WrongS NandaNo ratings yet
- 301 302 303 X03mapDocument1 page301 302 303 X03mapKyungJun ShinNo ratings yet
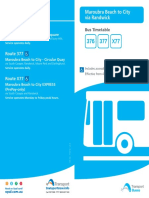
- 376 - 377 Bus Time TableDocument19 pages376 - 377 Bus Time TableBobNo ratings yet
- 376 - 377 Bus MapDocument1 page376 - 377 Bus MapBobNo ratings yet
- Hapter Xercise OlutionsDocument5 pagesHapter Xercise OlutionsBobNo ratings yet
- International: 2020 VisionDocument5 pagesInternational: 2020 VisionBobNo ratings yet
- 376 - 377 Bus Time TableDocument19 pages376 - 377 Bus Time TableBobNo ratings yet
- Takaful: An Islamic Alternative To Conventional Insurance Sees Phenomenal GrowthDocument3 pagesTakaful: An Islamic Alternative To Conventional Insurance Sees Phenomenal GrowthBobNo ratings yet
- Pension Benefit Design: Flexibility and The Integration of Insurance Over The Life CycleDocument43 pagesPension Benefit Design: Flexibility and The Integration of Insurance Over The Life CycleBobNo ratings yet
- Draft Standards For The Development of Spreadsheets: 1 Spreadsheets Can Be AssetsDocument5 pagesDraft Standards For The Development of Spreadsheets: 1 Spreadsheets Can Be AssetsBobNo ratings yet
- Is Insurance A Luxury?Document3 pagesIs Insurance A Luxury?BobNo ratings yet
- It's Time To Abolish Retirement (And Here's How To Do It) .: Work, Learn and Play Till You DropDocument47 pagesIt's Time To Abolish Retirement (And Here's How To Do It) .: Work, Learn and Play Till You DropBobNo ratings yet
- ch4 5Document37 pagesch4 5BobNo ratings yet
- Signs of Ageing: HealthcareDocument2 pagesSigns of Ageing: HealthcareBobNo ratings yet
- ch4 1Document42 pagesch4 1BobNo ratings yet
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeFrom EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeRating: 4 out of 5 stars4/5 (5794)
- The Yellow House: A Memoir (2019 National Book Award Winner)From EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Rating: 4 out of 5 stars4/5 (98)
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryFrom EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryRating: 3.5 out of 5 stars3.5/5 (231)
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceFrom EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceRating: 4 out of 5 stars4/5 (895)
- The Little Book of Hygge: Danish Secrets to Happy LivingFrom EverandThe Little Book of Hygge: Danish Secrets to Happy LivingRating: 3.5 out of 5 stars3.5/5 (400)
- Shoe Dog: A Memoir by the Creator of NikeFrom EverandShoe Dog: A Memoir by the Creator of NikeRating: 4.5 out of 5 stars4.5/5 (537)
- Never Split the Difference: Negotiating As If Your Life Depended On ItFrom EverandNever Split the Difference: Negotiating As If Your Life Depended On ItRating: 4.5 out of 5 stars4.5/5 (838)
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureFrom EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureRating: 4.5 out of 5 stars4.5/5 (474)
- Grit: The Power of Passion and PerseveranceFrom EverandGrit: The Power of Passion and PerseveranceRating: 4 out of 5 stars4/5 (588)
- The Emperor of All Maladies: A Biography of CancerFrom EverandThe Emperor of All Maladies: A Biography of CancerRating: 4.5 out of 5 stars4.5/5 (271)
- On Fire: The (Burning) Case for a Green New DealFrom EverandOn Fire: The (Burning) Case for a Green New DealRating: 4 out of 5 stars4/5 (74)
- Team of Rivals: The Political Genius of Abraham LincolnFrom EverandTeam of Rivals: The Political Genius of Abraham LincolnRating: 4.5 out of 5 stars4.5/5 (234)
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaFrom EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaRating: 4.5 out of 5 stars4.5/5 (266)
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersFrom EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersRating: 4.5 out of 5 stars4.5/5 (344)
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyFrom EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyRating: 3.5 out of 5 stars3.5/5 (2259)
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreFrom EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreRating: 4 out of 5 stars4/5 (1090)
- The Unwinding: An Inner History of the New AmericaFrom EverandThe Unwinding: An Inner History of the New AmericaRating: 4 out of 5 stars4/5 (45)
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)From EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Rating: 4.5 out of 5 stars4.5/5 (121)
- Her Body and Other Parties: StoriesFrom EverandHer Body and Other Parties: StoriesRating: 4 out of 5 stars4/5 (821)
- Ch6 Statistical HydrologyDocument16 pagesCh6 Statistical HydrologykundanNo ratings yet
- CVEN2002 Laboratory ExercisesDocument41 pagesCVEN2002 Laboratory ExercisesMary DinhNo ratings yet
- Questions and Answers On Unit Roots, Cointegration, Vars and VecmsDocument6 pagesQuestions and Answers On Unit Roots, Cointegration, Vars and VecmsTinotenda DubeNo ratings yet
- Probability, AUC, and Excel Linest FunctionDocument2 pagesProbability, AUC, and Excel Linest FunctionWathek Al Zuaiby0% (1)
- Periodic Table of The ElementsDocument36 pagesPeriodic Table of The ElementsJayakaran PachiyappanNo ratings yet
- Evaluation of Ambient Noise Levels in Port Harcourt Metropolis, South-South, NigeriaDocument7 pagesEvaluation of Ambient Noise Levels in Port Harcourt Metropolis, South-South, NigeriaIOSRjournalNo ratings yet
- Beetroot Core PracticalDocument15 pagesBeetroot Core PracticalSanngeeta100% (1)
- 03 Probability DistributionDocument3 pages03 Probability DistributionLKS-388No ratings yet
- Bayes GaussDocument29 pagesBayes GaussYogesh Nijsure100% (1)
- Fungicide Programs Used To Manage Powdery Mildew Erysiphe Ne - 2021 - Crop ProtDocument11 pagesFungicide Programs Used To Manage Powdery Mildew Erysiphe Ne - 2021 - Crop ProtIlija MileticNo ratings yet
- Analysis of Factors Affecting The Winning Percentage ODI Cricket MatchesDocument24 pagesAnalysis of Factors Affecting The Winning Percentage ODI Cricket MatchesVenu Gopal Vegi0% (1)
- Silk Reeling and Testing Manual. Chapter 2Document11 pagesSilk Reeling and Testing Manual. Chapter 2Vipin Singh KandholNo ratings yet
- 2024 State Competition Sprint RoundDocument8 pages2024 State Competition Sprint Roundshimmiguel00No ratings yet
- Inference About A Population VarianceDocument17 pagesInference About A Population VarianceIves LeeNo ratings yet
- Guia Diseño Aashto 93Document626 pagesGuia Diseño Aashto 93Geoffrey Collantes JulcaNo ratings yet
- Basic Statistics Formula SheetDocument5 pagesBasic Statistics Formula SheetHéctor FloresNo ratings yet
- Experiment 9 - DryingDocument10 pagesExperiment 9 - DryingMelike SucuNo ratings yet
- Skittles FinalDocument12 pagesSkittles Finalapi-241861434No ratings yet
- Mechanical Engineering Objective Type Questions For ExamsDocument7 pagesMechanical Engineering Objective Type Questions For ExamsSagarias AlbusNo ratings yet
- Assignment 1Document6 pagesAssignment 1Griffin William UnderwoodNo ratings yet
- Quantum XLExampleDocument83 pagesQuantum XLExamplesankar22No ratings yet
- Statistical Process Control.Document26 pagesStatistical Process Control.foofoolNo ratings yet
- Crop Yield PredictionDocument6 pagesCrop Yield PredictionVartul Tripathi100% (1)
- Materials of Construction and TestingDocument58 pagesMaterials of Construction and TestingChristian BaldoNo ratings yet
- Forecasting Long Range Dependent Time Series With Exogenous Variable Using ARFIMAX ModelDocument4 pagesForecasting Long Range Dependent Time Series With Exogenous Variable Using ARFIMAX ModelKrishna SarkarNo ratings yet
- Statistical Inference, Econometric Analysis and Matrix Algebra. Schipp, Bernhard Krämer, Walter. 2009Document445 pagesStatistical Inference, Econometric Analysis and Matrix Algebra. Schipp, Bernhard Krämer, Walter. 2009José Daniel Rivera MedinaNo ratings yet
- GraphPad Prism SlidesDocument79 pagesGraphPad Prism SlidesVasincuAlexandruNo ratings yet
- Traffic Prediction - Using AIDocument15 pagesTraffic Prediction - Using AIDhanvini BasavaNo ratings yet
- Lecture 8 - StatisticsDocument21 pagesLecture 8 - StatisticsMohanad SulimanNo ratings yet
- Every Number CountsDocument5 pagesEvery Number CountsGary GohNo ratings yet