Professional Documents
Culture Documents
The First Derivative: Types of Stationary Points
Uploaded by
api-19505025Original Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
The First Derivative: Types of Stationary Points
Uploaded by
api-19505025Copyright:
Available Formats
GITIMH3 94107 Geometrical Applications of Differentiation Page 1
The First Derivative
11/11/98
To See How To Differentiate See Differentiation
The point on the curve is increasing when f’(x) > 0
The point on the curve is decreasing when f’(x) < 0
The point on the curve is stationary when f’(x) = 0
f’(x) < 0 f’(x) > 0
f’(x) = 0
Types of Stationary Points:
Local Minimum Point
x LHS MIN RH
S
f’(x) <0 0 >0
Local Maximum Point
x LHS MA RHS
X
f’(x) >0 0 <0
Point of Horizontal Inflection
(1) (2)
x LHS PT RHS
1 f’(x) <0 0 <0
2 f’(x) >0 0 >0
Luke Cole Page 1
GITIMH3 94107 Geometrical Applications of Differentiation Page 2
E.g. (1) Find all ‘x’ values for which the curve f(x) = x2 – 4.x + 1 is decreasing
A f(x) = x2 – 4.x + 1
f’(x) = 2.x – 4
So, 2.x – 4 < 0 for a decreasing point
x<2
E.g. (2) Find the stationary points of y = x3 – 48.x – 7
dy
A 3.x 2 48
dx
So, 3.x2 – 48 = 0 for stationary points
x=4
Subbing x = 4 into equation
(4, 135) & ( 4, 121)
E.g. (3) Determine the types of stationary points for y = x3
dy
A 3.x 2 0 for stationary points
dx
x=0
So, x 0 0 0+
dy + 0 +
dx
The Type of stationary point is: Horizontal point of infection
Luke Cole Page 2
GITIMH3 94107 Geometrical Applications of Differentiation Page 3
The Second Derivative
12/11/98
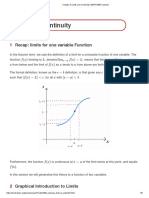
The curve is concave up when f’’(x) > 0
The curve is concave down when f’’(x) < 0
There is a point of inflection when f’’(x) = 0 and concavity changes
f’’(x) < 0 f’’(x) = 0
f’’(x) > 0
Types of Stationary Points:
Local Minimum Point
x LHS MIN RH
S
f’(x) <0 0 >0
or
f’’(x) > 0
Maximum Stationary Point
x LHS MA RHS
X
f’(x) >0 0 <0
or
f’’(x) < 0
Point of Inflection
(1) x LHS PT RH (2)
S
1 f’’(x) <0 0 >0
2 f’’(x) >0 0 <0
Luke Cole Page 3
GITIMH3 94107 Geometrical Applications of Differentiation Page 4
E.g. (1) If f(x) = 2.x3 7.x2 5.x + 4, find where f(x) is concave down
A f’(x) = 6x2 – 14x – 5
f’’(x) = 12.x – 14
So, 12.x – 4 < 0 for concave down curves
x < 7/6
7
/6
E.g. (2) Find the point of inflection of y = x3 – 6.x2 + 5.x + 9
dy
A 3.x 2 12.x 5
dx
d2y
2
6.x 12.x 2 0 for points of inflection
dx
So, x=2&y=3
And, x 2 2 2+
d2y 0 +
Concavity Changes
dx 2
(2, 3) is a point of inflection
E.g. (3) Graph y = x4
Luke Cole Page 4
GITIMH3 94107 Geometrical Applications of Differentiation Page 5
dy
A 4.x 3 0 for stationary points
dx
So, x=0
d2y
2
12.x 2
dx
d2y
At, x=0 0
dx 2
And, x 0 0 0+
d2y + 0 +
Concavity doesn’t change
dx 2
Since f’(x) = 0 & f’’(x) = 0 but doesn’t change concavity, no point of
inflection so:
dy
From, 4.x 3
dx
x 0 0 0+
dy 0 +
dx
Luke Cole Page 5
GITIMH3 94107 Geometrical Applications of Differentiation Page 6
Curve Sketching
16/11/98
Sketching Curves Involves:
Stationary points
Points of inflection
‘x’ and ‘y’ intercepts
Domain and Range
Asymptotes and limits
Establish if odd or even
If needed draw a table of values
E.g. Sketch the curve, y = 2.x3 + 3.x2 12.x 13
A Finding Stationary Points
dy
6.x 2 6.x 12 0 for stationary points
dx
x=2 & x=1
y=7 y = 20
x 2 2+ x 1 1 1+
2 dy 0 +
dy + 0 dx
dx
( 2, 7) maximum & (1, 20) minimum
Finding Points of Inflection
d2y
12.x 6 0 for points of inflection
dx 2
x=½
y = 6½
x 6½ 6½+
6½
dy 0 +
dx
( ½, 6½) is a point of inflection
Luke Cole Page 6
GITIMH3 94107 Geometrical Applications of Differentiation Page 7
Finding ‘x’ & ‘y’ Intercepts
Let, x = 0 for y-intercepts:
y = 13
Let, y = 0 for x-intercepts:
0 = 2.x3 + 3.x2 12.x 13
Since, 2x2 + x 13 is divisible by x + 1:
i.e. (x+ 1)(2.x2 + x 13) = 0
x=1 & x 2.3, 2.8
Finding Domain and Range
So, 2.x3 + 3.x2 12.x 13 All Real:
Domain = All Real
Since, y = 2.x3 + 3.x2 12.x 13:
Range = All Real
Since domain and range are all real there is on limits or asymptotes
Sketch
( 2, 7) y
(1, 20)
Luke Cole Page 7
GITIMH3 94107 Geometrical Applications of Differentiation Page 8
Maximum and Minimum
When asked to find the maximum (not local max) it’s the greatest value for ‘y’
When asked to find the minimum (not local min) it’s the smallest value for ‘y’
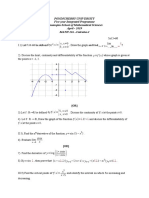
E.g. Find the max and min values for the function y = x4 2.x2 + 1 for 2 x 3
A …
…
Sketch in the domain 2 x 3
MAX
So, MAX y = 64
MIN y = 0
MIN
Luke Cole Page 8
GITIMH3 94107 Geometrical Applications of Differentiation Page 9
Maxima and Minima Problems
E.g. The council wishes to make a rectangular swimming area at the beach using a
straight cliff on one side and a length of 300m of shark pool netting for the other
3 sides what are the dimensions of the rectangle that encloses the greatest area?
A Perimeter
P = 2.x + y = 300 …(1)
Area
A = x.y …(2)
(1) y = 300 2.x …(3)
Now sub (2) into (3) x
A = x(300 2.x)
= 300.x 2.x2
Max area y
dA
300 4.x 0 for stationary points
dx
x = 75
x 75 75 75+
dA + 0
dx
Dimensions are x = 75 & y = 150
Luke Cole Page 9
GITIMH3 94107 Geometrical Applications of Differentiation Page 10
Primitive Functions
Primitive functions is finding f(x) knowing f’(x)
x n 1
If, f’(x) = xn When, f x C
n1
C = Constant
E.g. (1) Find f(x) from f’(x) = x5 4.x3
x 6 4.x 4
So, f x C
6 4
= 1 6 .x 6 x 4 C
E.g. (2) If f’’(x) = 6.x + 2 and f’(1) = 0 and f( 2) = 0 find f(3)
A Here, f’(x) = 3.x2 + 2.x + C
Since, f’(1) = 0 = 3(1)2 + 2(1) + C
C=5
So, f’(x) = 3.x2 + 2.x 5
Now, f(x) = x3 + x2 5.x + C
Since, f( 2) = 0 = ( 2)3 + ( 2)2 5( 2) + C
C=6
f(x) = x3 + x2 5.x 6
f(3) = 15
Luke Cole Page 10
You might also like
- Lecture 2Document11 pagesLecture 2MeryemNo ratings yet
- 5, X 0 Lim: Byf (X) X, X 0Document2 pages5, X 0 Lim: Byf (X) X, X 0Ilamurugan INo ratings yet
- Calculus, Probability, and Statistics Primers: Dave GoldsmanDocument104 pagesCalculus, Probability, and Statistics Primers: Dave Goldsmanbanned minerNo ratings yet
- Homework Session 2 Flows On The Line: 2.4 Linear Stability AnalysisDocument6 pagesHomework Session 2 Flows On The Line: 2.4 Linear Stability AnalysisAaaereNo ratings yet
- Chapter 3 Limits and Continuity - MATH1006 CalculusDocument8 pagesChapter 3 Limits and Continuity - MATH1006 CalculusHerkhinwale OmoakinNo ratings yet
- MIT OpenCourseWare Http://Ocw - Mit.eduDocument41 pagesMIT OpenCourseWare Http://Ocw - Mit.eduAdamNo ratings yet
- Splitted 2. - Calculus - Schaums - Fifth - Edition-86-102-DikonversiDocument5 pagesSplitted 2. - Calculus - Schaums - Fifth - Edition-86-102-DikonversiGulu GuluNo ratings yet
- One Dimensional FlowsDocument19 pagesOne Dimensional FlowsBhawan NarineNo ratings yet
- For More Important Questions Visit:: Applications of DerivativesDocument14 pagesFor More Important Questions Visit:: Applications of DerivativesRutva Paresh BabariaNo ratings yet
- Continuous Random Variable Density FunctionDocument11 pagesContinuous Random Variable Density FunctionTom WhanNo ratings yet
- 27 Tangent Planes and Linear ApproximationDocument23 pages27 Tangent Planes and Linear ApproximationKouji TomasNo ratings yet
- 4.2 (Cont.) Standard Deviation of A Discrete Random VariableDocument33 pages4.2 (Cont.) Standard Deviation of A Discrete Random Variableshiela valdemoroNo ratings yet
- DiferentiabilityDocument24 pagesDiferentiabilitypau miquelNo ratings yet
- PDE - S and Transition Density FunctionDocument44 pagesPDE - S and Transition Density FunctionParitoshNo ratings yet
- Orddiffsolnlesson 8Document7 pagesOrddiffsolnlesson 8Graham MooreNo ratings yet
- Limits and Continuity ChapterDocument11 pagesLimits and Continuity ChapterSashaNo ratings yet
- One Dimensional Taylor SeriesDocument4 pagesOne Dimensional Taylor Serieseddyedwards511No ratings yet
- UntitledDocument4 pagesUntitledPRINCE KUMARNo ratings yet
- Topic 6. Calculus PDFDocument100 pagesTopic 6. Calculus PDFAYushi SarafNo ratings yet
- 10.1 2D Alignment LLSDocument28 pages10.1 2D Alignment LLSD21L243 -Hari Vignesh S KNo ratings yet
- AdvStats - W4 - ContinousDocument24 pagesAdvStats - W4 - ContinousPedro FernandezNo ratings yet
- APMA 0160 (A. Yew) Spring 2011 - Numerical Differentiation Finite DifferencesDocument2 pagesAPMA 0160 (A. Yew) Spring 2011 - Numerical Differentiation Finite DifferencesNazifa NawerNo ratings yet
- DIFFERENTIATION & FUNCTIONS (Q 6, 7 & 8, PAPER 1Document7 pagesDIFFERENTIATION & FUNCTIONS (Q 6, 7 & 8, PAPER 1Graham MooreNo ratings yet
- Chapter 4: Unconstrained OptimizationDocument25 pagesChapter 4: Unconstrained OptimizationcucrasNo ratings yet
- MTU07305 Lecture 2-Roots of Functions Using Iterative MethodsDocument18 pagesMTU07305 Lecture 2-Roots of Functions Using Iterative MethodsKrizzy krizNo ratings yet
- Finding Derivatives and Tangent SlopesDocument24 pagesFinding Derivatives and Tangent SlopesLiliana AmpNo ratings yet
- Diferent I AbilityDocument24 pagesDiferent I AbilityLiliana AmpNo ratings yet
- Unit 3 DifferentiationDocument41 pagesUnit 3 Differentiationieman najmiNo ratings yet
- (Chapter 6) DifferentiationDocument27 pages(Chapter 6) DifferentiationdenixngNo ratings yet
- Turning PointsDocument20 pagesTurning PointsRachelle ParedesNo ratings yet
- Concept of Local Maximum and Local Minimum Local Maximum: 1. First Derivative Test: IfDocument5 pagesConcept of Local Maximum and Local Minimum Local Maximum: 1. First Derivative Test: IfAyush SrivastavNo ratings yet
- EC2303 Additional Practice QuestionsDocument7 pagesEC2303 Additional Practice QuestionsSiya LimNo ratings yet
- Sheet - 01 - DifferentiabilityDocument26 pagesSheet - 01 - DifferentiabilityMankirat SinghNo ratings yet
- Engineering Prob & Stat Lecture Notes 6Document12 pagesEngineering Prob & Stat Lecture Notes 6EICQ/00154/2020 SAMUEL MWANGI RUKWARONo ratings yet
- Https App - Oswaalbooks.com Download Sample-Qp Subsolution 350SAP-3 SolDocument11 pagesHttps App - Oswaalbooks.com Download Sample-Qp Subsolution 350SAP-3 Sol3107aloksinghNo ratings yet
- Continuous Functions: 1 ConceptDocument5 pagesContinuous Functions: 1 Concept01. ZUENo ratings yet
- HW 5 Arc F04Document7 pagesHW 5 Arc F04jordangeorge.66jNo ratings yet
- TALectureNotes W3Document19 pagesTALectureNotes W3簡千翔No ratings yet
- Differential Calculus in a NutshellDocument32 pagesDifferential Calculus in a NutshellBagoes Budi LaksonoNo ratings yet
- Lecture13 CaiDocument20 pagesLecture13 CaiWilliam Sin Chau WaiNo ratings yet
- Lecture Notes On Differentiation MATH161 PDFDocument12 pagesLecture Notes On Differentiation MATH161 PDFalchemistNo ratings yet
- UPSC Civil Services Main 1983 - Mathematics Calculus: Sunder LalDocument7 pagesUPSC Civil Services Main 1983 - Mathematics Calculus: Sunder Lalsayhigaurav07No ratings yet
- Maths-Pt-1 SolutionDocument6 pagesMaths-Pt-1 SolutionRaju SinghNo ratings yet
- Numerical DifferentiationDocument26 pagesNumerical Differentiationneil mempinNo ratings yet
- Unit 4 - Continuous Random VariablesDocument35 pagesUnit 4 - Continuous Random VariablesShouq AbdullahNo ratings yet
- Basic Differentiation Rules for Calculus I (NYUDocument100 pagesBasic Differentiation Rules for Calculus I (NYUAudie T. MataNo ratings yet
- Instantaneous Rate of Change - The DerivativeDocument7 pagesInstantaneous Rate of Change - The DerivativeTrishul GyNo ratings yet
- Power Series and Differential Equations: The Method of FrobeniusDocument25 pagesPower Series and Differential Equations: The Method of Frobeniusomotoriogun samuelNo ratings yet
- UNIT-1 (Limits and Continuity)Document2 pagesUNIT-1 (Limits and Continuity)Dheeraj Krishna NeelamNo ratings yet
- MA 101 (Mathematics - I) : Differentiation: Exercise Set 2Document1 pageMA 101 (Mathematics - I) : Differentiation: Exercise Set 2AdityaNo ratings yet
- P1 - Chapter Review 8Document4 pagesP1 - Chapter Review 8more ProfitsNo ratings yet
- Maxima, Minima, Rolle's Theorem & DerivativesDocument2 pagesMaxima, Minima, Rolle's Theorem & DerivativesvishaldeepNo ratings yet
- Pertemuan Ke 4 Kalkulus IDocument6 pagesPertemuan Ke 4 Kalkulus IBintang BintangNo ratings yet
- Week 4 Quiz: Differential Calculus: Uses of The Derivative: Increasing and Decreasing FunctionsDocument7 pagesWeek 4 Quiz: Differential Calculus: Uses of The Derivative: Increasing and Decreasing Functionsatharva deshpandeNo ratings yet
- ECO4112F Section 2 Comparative StaticsDocument50 pagesECO4112F Section 2 Comparative StaticsAhmad ZakiNo ratings yet
- HIGHER DERIVATIVESDocument6 pagesHIGHER DERIVATIVESHarry PotterNo ratings yet
- L31 - Non-Linear Programming Problems - Unconstrained Optimization - KKT ConditionsDocument48 pagesL31 - Non-Linear Programming Problems - Unconstrained Optimization - KKT ConditionsNirmit100% (1)
- Probability Homework 3: Key ConceptsDocument3 pagesProbability Homework 3: Key ConceptsYuliVelozNo ratings yet
- Green's Function Estimates for Lattice Schrödinger Operators and Applications. (AM-158)From EverandGreen's Function Estimates for Lattice Schrödinger Operators and Applications. (AM-158)No ratings yet
- On the Tangent Space to the Space of Algebraic Cycles on a Smooth Algebraic Variety. (AM-157)From EverandOn the Tangent Space to the Space of Algebraic Cycles on a Smooth Algebraic Variety. (AM-157)No ratings yet
- Counting Techniques:: GIKPKC7 94107 Permutations & CombinationsDocument3 pagesCounting Techniques:: GIKPKC7 94107 Permutations & Combinationsapi-19505025No ratings yet
- Wired Equivalent Privacy: (WEP) : 17th of April, 2003Document6 pagesWired Equivalent Privacy: (WEP) : 17th of April, 2003api-19505025No ratings yet
- Ipv 6Document5 pagesIpv 6api-19505025No ratings yet
- Drawing Using The Scorbot Manipulator ArmDocument17 pagesDrawing Using The Scorbot Manipulator Armlfc_hotmail4253No ratings yet
- Trigonometric Ratios:: Sine Cosine TangentDocument12 pagesTrigonometric Ratios:: Sine Cosine Tangentapi-19505025No ratings yet
- Autonomous LEGO C Climber Project - StingrayDocument12 pagesAutonomous LEGO C Climber Project - Stingrayapi-19505025No ratings yet
- Monte Carlo Localisation For Mobile Robots: 31st of May, 2006Document4 pagesMonte Carlo Localisation For Mobile Robots: 31st of May, 2006api-19505025No ratings yet
- The Binomial TheoremDocument4 pagesThe Binomial Theoremapi-19505025No ratings yet
- Monte Carlo Localisation For Mobile Robots: 31st of May, 2006Document16 pagesMonte Carlo Localisation For Mobile Robots: 31st of May, 2006api-19505025No ratings yet
- Definitions:: General FormDocument8 pagesDefinitions:: General Formapi-19505025No ratings yet
- Terms:: Asymptote Continuous Discontinuous DerivativeDocument9 pagesTerms:: Asymptote Continuous Discontinuous Derivativeapi-19505025No ratings yet
- Notation:: Range of ProbabilityDocument6 pagesNotation:: Range of Probabilityapi-19505025No ratings yet
- Terms:: The Real Number SystemDocument11 pagesTerms:: The Real Number Systemapi-19505025No ratings yet
- Sequences: Sigma Notation (Document8 pagesSequences: Sigma Notation (api-19505025No ratings yet
- Approximation Methods: The Trapezoidal RuleDocument5 pagesApproximation Methods: The Trapezoidal Ruleapi-19505025No ratings yet
- Independent / Dependant Variables:: ValueDocument11 pagesIndependent / Dependant Variables:: Valueapi-19505025No ratings yet
- Polynomials IIDocument3 pagesPolynomials IIapi-19505025No ratings yet
- Localisation Using Active Mirror Vision System: Luke Cole (U4014181) Supervised by Dr. David AustinDocument17 pagesLocalisation Using Active Mirror Vision System: Luke Cole (U4014181) Supervised by Dr. David Austinapi-19505025No ratings yet
- ParabolaDocument12 pagesParabolaapi-19505025No ratings yet
- Matrices: A Complete CourseDocument22 pagesMatrices: A Complete Courseapi-19505025No ratings yet
- Co-Ordinate GeometryDocument5 pagesCo-Ordinate Geometryapi-19505025No ratings yet
- GeometryDocument8 pagesGeometryapi-19505025No ratings yet
- Complex NumbersDocument21 pagesComplex Numbersapi-19505025No ratings yet
- Localisation Using Active Mirror Vision System-Anu05Document55 pagesLocalisation Using Active Mirror Vision System-Anu05api-19505025No ratings yet
- Conic SectionsDocument11 pagesConic Sectionsapi-19505025No ratings yet
- Circle GeometryDocument5 pagesCircle Geometryapi-19505025No ratings yet
- Insect Inspired Robots-Acra06Document6 pagesInsect Inspired Robots-Acra06api-19505025No ratings yet
- Airhockey Chi06 PosterDocument1 pageAirhockey Chi06 Posterapi-19505025No ratings yet
- Airhockey Pergames06Document7 pagesAirhockey Pergames06api-19505025No ratings yet
- Assignment 3 Differential Equation and Laplace TransformDocument2 pagesAssignment 3 Differential Equation and Laplace TransformJunior Paul BalenNo ratings yet
- Derivations of maximum flow models for transportation systems engineeringDocument3 pagesDerivations of maximum flow models for transportation systems engineeringReinold NdreuNo ratings yet
- Detailed Lesson Plan in Mathematics 6Document6 pagesDetailed Lesson Plan in Mathematics 6Ma. Jennifer Mapanoo100% (2)
- Data Representation and Digital ComputersDocument16 pagesData Representation and Digital Computersremyaresmi05No ratings yet
- U3-2 Method of Variation of ParametersDocument15 pagesU3-2 Method of Variation of ParametersR NishanNo ratings yet
- EDO IIT Guwahati PDFDocument359 pagesEDO IIT Guwahati PDFBruno QueirozNo ratings yet
- Finite Difference Method: ME710 Mathematical Methods For Engineers Mechanical Engineering NITK SurathkalDocument20 pagesFinite Difference Method: ME710 Mathematical Methods For Engineers Mechanical Engineering NITK SurathkalSantosh Kumar AgastiNo ratings yet
- Chapter2 MicroprocessorDocument95 pagesChapter2 MicroprocessorsagarNo ratings yet
- DE For EEDocument6 pagesDE For EEPaul Simon NacisNo ratings yet
- Formula 1Document2 pagesFormula 1Sampurna SharmaNo ratings yet
- Lesson Plan 12 07 - Subtraction Using Base Ten BlocksDocument3 pagesLesson Plan 12 07 - Subtraction Using Base Ten Blocksapi-385469985No ratings yet
- Salmiya Indian Model School Math Plan May-June 2020Document3 pagesSalmiya Indian Model School Math Plan May-June 2020Mehaboob BashaNo ratings yet
- Grade 7 Unit 5 Student PageDocument2 pagesGrade 7 Unit 5 Student Pageapi-237707754No ratings yet
- Post LabDocument25 pagesPost LabMugunthan KrishnaNo ratings yet
- 01 MTH401 (Updated Handouts)Document428 pages01 MTH401 (Updated Handouts)Muhammad HanzalaNo ratings yet
- Error FunctionDocument10 pagesError Functionprithviraj gavhaneNo ratings yet
- Solving First Order Differential EquationsDocument43 pagesSolving First Order Differential EquationsAnggoro Indarto AkbarNo ratings yet
- Derivatives, Integrals, Multiplication and Division by T Laplce Transforms by Michael PantonillaDocument21 pagesDerivatives, Integrals, Multiplication and Division by T Laplce Transforms by Michael PantonillaMichael PantonillaNo ratings yet
- Techniques in Numerical Reasoning TestDocument13 pagesTechniques in Numerical Reasoning Testatz Kusain100% (1)
- Lecture Computer CodesDocument87 pagesLecture Computer CodesKim Brian CarboNo ratings yet
- Weekly Home Learning Plan - KindergartenDocument3 pagesWeekly Home Learning Plan - KindergartenPrecious ArniNo ratings yet
- Formulas Derivatives Trigonometric FunctionsDocument7 pagesFormulas Derivatives Trigonometric FunctionsJoshuaNo ratings yet
- Derivative Rules and TechniquesDocument16 pagesDerivative Rules and TechniqueslegoNo ratings yet
- Math 0 - Module 1.2 PolynomialsDocument11 pagesMath 0 - Module 1.2 PolynomialsWhelance TomboconNo ratings yet
- Solution of First Order Differential Equations (Exact Differential Equations)Document37 pagesSolution of First Order Differential Equations (Exact Differential Equations)Nazeer SurchiNo ratings yet
- Ordinary Differential Equations - BAMAT-201Document256 pagesOrdinary Differential Equations - BAMAT-201Vanitha RamsNo ratings yet
- Unit - Iii - TpdeDocument15 pagesUnit - Iii - TpdeAmal_YaguNo ratings yet
- Methods of Solution of Selected Differential EquationsDocument7 pagesMethods of Solution of Selected Differential EquationsCHRISTINE NICOLE VICTORIONo ratings yet
- r17 STLD NotesDocument118 pagesr17 STLD NotesJNRNo ratings yet
- Beginning and Intermediate Algebra 6th Edition Lial Solutions ManualDocument90 pagesBeginning and Intermediate Algebra 6th Edition Lial Solutions ManualJamesWolfefsgr100% (45)