1

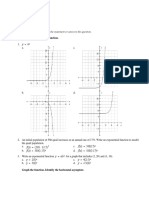
The hyperbolic end

Before you begin this problem set, set your calculator to show With a square scale, a distance of
1 unit in the x direction is the
same as the distance of 1 unit in
the y direction. Because
calculator screen are not squares,
giving the x and y axes the same
windows does not give a square
scale!
x values between 10 and 10, and y values between 10 and 10.
Then reset the window to a square scale. (On most calculators,
there is a ZOOM SQUARE setting.) This keeps the graphs from
being distorted.
1. The standard equation for an ellipse is
x
2
a
2
+
y
2
b
2
= 1. Let
If you worked through the
problem set The circle and its
cousins, you looked at equations
of the form
x
2
r
+
y
2
s
= 1. If both
r and s are positive, then a =

r
and b =

s. What happens to
the graph if only one of r and s is
positive?
a = 2 and b = 3, and graph this equation on your graph-
ing calculator using the window described above. (NOTE:
For a given y
2
, there are usually two values of y that are
possiblefor example, if y
2
is 4, y could be 2 or 2. You
need to graph two functions to get all of the ellipse on your
graph.)
(a) What are the lines of symmetry of this ellipse? Of a
general ellipse (
x
2
a
2
+
y
2
b
2
= 1)?
(b) What are the intercepts of this ellipse? Of a general
ellipse?
2. The standard equation for a hyperbola is
x
2
a
2

y
2
b
2
= 1. Let
The graph of the equation
y
2
a
2

x
2
b
2
= 1 is also a hyperbola.
When youve completed this
problem set, you might want to
try it again with this other
equation.
a = 2 and b = 3, and graph this equation on your graphing
calculator.
(a) What are the lines of symmetry of this hyperbola? Of
a general hyperbola (
x
2
a
2

y
2
b
2
= 1)?
(b) What are the intercepts of this hyperbola? Of a general
hyperbola?
3. Compare your answers to problems 1 and 2. What do they
have in common? What is dierent?
4. You should have been able to supply more information
about the ellipse than about the hyperbola. What pa-
rameters of the ellipse equation did you use to supply the
additional information?
Now lets see if you cant nd a way to use that parameter for
the hyperbola, too. (Call it the unused parameter for the
moment.)
5. Zoom out on your graph of the hyperbola several times,
until the shape looks dierent than it did (and then once
or twice more for good measure). Keep track of how many
times you zoomed out.
(a) What does the graph look like now?
Problems with a Point: April 1, 2002 c EDC 2002
The hyperbolic end: Problem 2
(b) Now, try to nd a dierent set of equations that
appears to give the same graph for this zoomed-out
window. Then graph the hyperbola and the equations
on the zoomed-out graph to verify that your equations
approximate the hyperbola in this window.
(c) How is the unused parameter used in your equations?
(d) Now, zoom in as many times as you zoomed out, so
youre back to the original window. How do the graphs
compare now?
The equations you found are asymptotes for the hyperbola:
As x gets more positive or more negative (getting further away
from the y-axis), the hyperbola gets closer to the asymptotes.
(However, the hyperbola will never actually touch or cross the
asymptotes.) Note: Some asymptotes can be
crossed, but not in the case of
hyperbolas.
6. What are the intercepts and asymptotes of the general
hyperbola,
x
2
a
2

y
2
b
2
= 1?
7. Use what you know about the graphs of a hyperbola to
make a reasonable graph, by hand, of the hyperbola with
equation
x
2
25

y
2
16
= 1. Do not graph it on your calculator
Hint: First nd the asymptotes
and draw them in using a dashed
line.
rst!
Problems with a Point: April 1, 2002 c EDC 2002
The hyperbolic end: Hints 1
Hints
Hint for problem 5b. It may be dicult to see any points
where the lines go through. One point should be easy, however
where they cross.
To nd another point on each, try just using the arrow but-
tons to move the cursor onto the line, or use the TRACE feature
to follow the hyperbola. Use a point as far from the other one
(the intersection point) as you can.
Hint for problem 5c. You may want to convert the numbers
in your equations to fractionsor nd fractions that are reason-
ably close to those numbers. As an extra hint, the parameters
of the hyperbola equation should show up in the fraction!
Problems with a Point: April 1, 2002 c EDC 2002
The hyperbolic end: Answers 1
Answers
1. (a) Lines of symmetry in both cases are the x- and y-axes.
(b) The x-intercepts of this ellipse are 2 and 2, and for
the general ellipse are a. The y-intercepts are 3
and 3 for this ellipse and b for the general ellipse.
2. (a) Lines of symmetry in both cases are the x- and y-axes.
(b) The x-intercepts of this ellipse are 2 and 2, and for
the general ellipse are a. (These hyperbolas have no
y-intercepts.)
3. The lines of symmetry and their x-intercepts are the same.
However, the ellipse has y-intercepts and the hyperbola
doesnt.
4. The parameter was b.
5. (a) It looks like two lines that go through the origin.
(b) Equations are y =
3
2
x and y =
3
2
x.
(c) Its the numerator of the slopes of the lines.
(d) The hyperbola is nestled between the lines, getting
closer as x gets more positive and more negative. It
looks like its trying to become the lines, in a way, or
like the hyperbola is being pulled toward the lines.
6. The intercepts are x = a and x = a, and the asymptotes Teachers Note: As an
extension, you might have your
students try to explain why these
are the asymptotes. Solving for y
gives y =
b
a

x
2
a
2
, or
y =
bx
a

1
a
2
x
2
. With a little
thought (and perhaps
experimenting with numerical
values), students should see that
these values get closer to
b
a
x as x
gets more positive or more
negative.
are y =
b
a
x and y =
b
a
x.
7. The intercepts are x = 5, and the asymptotes are y =

4
5
x. The following graph is more accurate than students
are expected to create; it is enough for them to have the
correct intercepts, asymptotes, and the general shape for
the hyperbola (curves that approach but dont touch the
asymptotes).
Problems with a Point: April 1, 2002 c EDC 2002
The hyperbolic end: Answers 2
Remember, the asymptotes are
not part of the graph of the
equationwhich is why they are
often drawn as dashed or dotted
lines.
Problems with a Point: April 1, 2002 c EDC 2002