Professional Documents
Culture Documents
Time: 3 Hour Total Marks: 100: Mathematics Class XII Sample Paper 1
Uploaded by
avi0341Original Description:
Original Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Time: 3 Hour Total Marks: 100: Mathematics Class XII Sample Paper 1
Uploaded by
avi0341Copyright:
Available Formats
CBSE XII | Mathematics
Sample Paper Sample paper set I
www.topperlearning.com 1
Mathematics
Class XII
Sample Paper 1
Time: 3 hour Total Marks: 100
1. All questions are compulsory.
2. The question paper consist of 29 questions divided into three sections A, B and C.
Section A comprises of 10 questions of one mar each, section B comprises of 12
questions of four mars each and section C comprises of 0! questions of si" mars
each.
#. All questions in Section A are to $e ans%ered in one %ord, one sentence or as per
the e"act requirement of the question.
&. There is no overall choice. 'o%ever, internal choice has $een provided in 0&
questions of four mars each and 02 questions of si" mars each. (ou have to
attempt only one of the alternatives in all such questions.
). *se of calculators is not permitted.
SECTION A
1. +f A , - a, $, c . and B , - 1, 2, # . and a function f / A B is 0iven $y
f , - 1a, 2 2 , 1 $ , # 2 , 1 c , 1 2 . . +s f a $i3ective function4
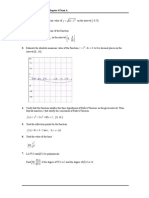
2. 5rom the 0raph of y , cos ", identify the intervals of " in %hich the function can $e
inverted.
3. +f A and B are square matrices of the same order. Chec %hether
1A 6 B2
2
, A
2
6 2AB 6 B
2
is true or not 4
4. +f a matri"
3 -4
A =
1 1
(
(
, Sho% that (A A') is a se% symmetric matri" , %here A' is
the transpose of matri" A.
5. +f A ,
2 3
3 4
| |
|
\
and
A
2,
5 18
18 7
| |
|
\
find
A
27 8A 6 1!+ .
CBSE XII | Mathematics
Sample Paper Sample paper set I
www.topperlearning.com 2
6. 5ind
2
1
dx
9 25x
7. 5ind a unit vector in the direction of
$
a 3i 2j 6k = +
r
$ $
.
8. 5ind the components and ma0nitude of the vector
uuur
PQ , %here 9 has coordinates 171,7
2,&2 and : has coordinates 12,0,722.
9. Sho% that the points A1#,7),12 , B 171, 0 , ;2 and C 1 ! , 710 , 782 are collinear.
10.
/2
7
- /2
Find sin xdx
SECTI! " #
11. <et A , : " :, : $ein0 the set of rationals. <et =>? $e a $inary operation on A, defined $y
1a, $2 > 1c, d2 , 1ac, ad 6 $2. Sho% that
1i2 =>? is not commutative 1ii2 =>? is associative
1iii2 The +dentity element %.r.t =>? is 11, 02
$
Let '*'be a binary operation on the set { !1!2!3!"!5# and
a$b i% a$b&6
a*b '
a$b-6 i% a$b 6
5ind the identity element and the inverse element of each element of the set
for the operation =>?.
12. Solve the @quation
-1 1
1-x
1$x
x!(x )
1
tan ' tan
2
>
| |
|
\
13. +s the 0iven function continuous at " , 04
1
x
1
x
e 1
! x
%(x)
e 1
! x
=
+
14. 5ind
2
dy
!*hen y ' a$ a$ a$x !*here a is a +onstant
dx
CBSE XII | Mathematics
Sample Paper Sample paper set I
www.topperlearning.com 3
15. Aiscuss the applica$ility of <a0ran0e?s Bean value theorem for the function/
%(x) ' sinx in the inter,a- - !
2 2
(
(
16.
dx
.,a-/ate the inte0ra-
1$x x
$
/2
-1
.,a-/ate sin2x tan (sinx)dx
17. 5orm the differential equation satisfied $y
2 2
(1 x ) (1 y ) ' a1(x - y) + =
%here
a is an ar$itrary constant.
18. Solve the differential equation 1"712dy 6 y d" , " 1"712 y
1C#
d"
$
2 3
dy
2o-,e the di%%erentia- e3/ation4 se+ y 2xtany x
dx
+ =
19. 5ind the an0le $et%een a
r
andb
r
. +f 0 a b c + + =
r r r
and a 3! b 5 5 + 7 = = =
r r r
$
= + = + Find i% the ,e+tors a i j 3k andb " i 5 j 2k
are perpendi+/-ar to ea+h other1
20. 5ind the distance of the point 12, &, 712 from the line
x 5 y 3 6 6
1 " 9
+ +
= =
21. A die is tossed thrice. 5ind the pro$a$ility of 0ettin0 an odd num$er at least once.
22. 5ind the interval in %hich the value of the determinant of the matri" A lies.
1 1
1 sin 1
7i,en 8' -sin 1 sin
sin
(
(
(
(
CBSE XII | Mathematics
Sample Paper Sample paper set I
www.topperlearning.com 4
SECTI! " C
23. 5ind A
71
, $y usin0 elementary ro% transformations. Diven
2 3 3
A = 2 2 3
3 2 2
(
(
(
(
.
24. Sho% that the hei0ht of the cylinder of 0reatest volume that can $e inscri$ed in a ri0ht
circular cone of hei0ht h and havin0 semi vertical an0le is one third that of the cone
and the 0reatest volume of cylinder is
3 2
"
h tan
27
25. 9rove that the curves y , "
2
and " , y
2
divide the square $ounded $y
" , 0, y,0, " , 1 and y,1 into three parts that are equal in area.
26. The chances of a patient havin0 a heart attac is &0E. Accordin0 to latest research
Aru0 A reduces the ris of heart attac $y #0E and dru0 B reduces its chances $y
2)E. At a time a patient can choose any one of the t%o options %ith equal
pro$a$ilities. +t is 0iven that after 0oin0 throu0h one of the t%o options the patient
selected at random
Suffers a heart attac. 5ind the pro$a$ility that the patient had $een prescri$ed Aru0 A.
$
A factory manufactures scre%s, machines F, ( and G manufacture respectively
1000,2000, #000 of the scre%s,1E, 1.)E and 2 E of their outputs are respectively
defective .A scre% is dra%n at random from the product and is found to $e defective.
Hhat is the pro$a$ility that it is manufactured $y the machine F 4
27. 5ind the equation of t%o lines throu0h the ori0in %hich intersect the line
3 3
at angles of
2 1 1 3
x y z
= = .
28. 5ind
( )
"
2
x 1dx
x 1)(x 1) +
$
5ind
( +ot x tanx)1dx +
29. T%o tailors A and B earn Is 1)0 and Is 200 per day respectively. A can stitch 8 shirts
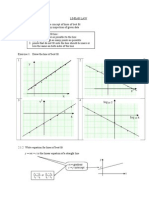
and & pants per day %hile B can stitch 10 shirts and & pants per day. 'o% many days
shall each %or, if it is desired to produce atleast 80 shirts and #2 pants at a minimum
la$our cost4 Solve the pro$lem 0raphically.
You might also like
- SPM Add Maths Formula List Form5Document28 pagesSPM Add Maths Formula List Form5Sayantani GhoshNo ratings yet
- Class - XI Subject - Mathematics: General InstructionsDocument5 pagesClass - XI Subject - Mathematics: General InstructionsDipankar Narendra AryaNo ratings yet
- Answer All Questions: Solve The Simultaneous Equations Selesaikan Persamaan Serentak 4x + y - 5 0Document8 pagesAnswer All Questions: Solve The Simultaneous Equations Selesaikan Persamaan Serentak 4x + y - 5 0saifolizamNo ratings yet
- AMC Years 11 and 12 (Senior) 2001 SOLUTIONSDocument5 pagesAMC Years 11 and 12 (Senior) 2001 SOLUTIONSDylan YapNo ratings yet
- Sample Paper-04 (Solved) Mathematics Class - XIDocument2 pagesSample Paper-04 (Solved) Mathematics Class - XIkishor0786No ratings yet
- Chemistry Test Class XDocument3 pagesChemistry Test Class XVedSachdevaNo ratings yet
- Sample Paper MathematicsDocument6 pagesSample Paper MathematicsAimee Layson PolancoNo ratings yet
- I.S.F.D y T. #103: Profesorado de Técnicos Prof: Martín MellerDocument11 pagesI.S.F.D y T. #103: Profesorado de Técnicos Prof: Martín MellerAriel LeucipoNo ratings yet
- (WWW - Entrance-Exa12 M.net) - IsC Class 12 Mathematics Sample Paper 6Document5 pages(WWW - Entrance-Exa12 M.net) - IsC Class 12 Mathematics Sample Paper 6Jennifer StevensonNo ratings yet
- EXAM MAT093 Sept 2013 I LearnDocument4 pagesEXAM MAT093 Sept 2013 I LearnNor HafizahNo ratings yet
- 2 Quadratic EqnDocument20 pages2 Quadratic EqnFam Sin YunNo ratings yet
- Equations. ActivitiesDocument2 pagesEquations. ActivitiesgringasNo ratings yet
- Sample Paper - 2012 Class - XII Subject - : Mathematics Time:3hrs Maximum Marks: 100Document6 pagesSample Paper - 2012 Class - XII Subject - : Mathematics Time:3hrs Maximum Marks: 100neela94No ratings yet
- Preparatory Problems For 1st YearsDocument25 pagesPreparatory Problems For 1st Yearswnasir123No ratings yet
- Square Roots and Cube Roots: Important Facts and FormulaeDocument5 pagesSquare Roots and Cube Roots: Important Facts and FormulaeshashankniecNo ratings yet
- Klinik Set1Document9 pagesKlinik Set1Nur WanNo ratings yet
- Q.E For Grade 7 (Answer Key)Document5 pagesQ.E For Grade 7 (Answer Key)Rogelio PontejoNo ratings yet
- MTH 401Document12 pagesMTH 401humza8081100% (1)
- Csec Mathematics Past Paper Solution - Jan 2008: Cxcdirect InstituteDocument12 pagesCsec Mathematics Past Paper Solution - Jan 2008: Cxcdirect Institutestyles_2980No ratings yet
- Discrete Random Variables: IntegralDocument7 pagesDiscrete Random Variables: IntegralKanchana RandallNo ratings yet
- Sample Paper-03 (Solved) Mathematics Class - XIDocument2 pagesSample Paper-03 (Solved) Mathematics Class - XIkishor0786No ratings yet
- 2014 2013 Math, Physics, ChemistryDocument30 pages2014 2013 Math, Physics, ChemistryMolay AdhikaryNo ratings yet
- Stewart - Calculus ET 6e Chapter 4 Form ADocument4 pagesStewart - Calculus ET 6e Chapter 4 Form AHarrison MeridaNo ratings yet
- Q2 LAS Math8 Wk1Document7 pagesQ2 LAS Math8 Wk1MIRAFLOR CUARTERONo ratings yet
- Section-A: 2 5 1 If 1,, - Find X and Y. 3 3 3 3Document5 pagesSection-A: 2 5 1 If 1,, - Find X and Y. 3 3 3 3Mayuri DuttaNo ratings yet
- CXC Mathematics Tutorial: Author: John Spencer MBA (Dist), M. SC, B. SCDocument9 pagesCXC Mathematics Tutorial: Author: John Spencer MBA (Dist), M. SC, B. SCPerry SinNo ratings yet
- Emath and Amath FormulaDocument21 pagesEmath and Amath FormulaveryveryhappyfeetNo ratings yet
- Sample Paper Half - Yearly Examination (2012 - 2013)Document3 pagesSample Paper Half - Yearly Examination (2012 - 2013)lock_jaw30No ratings yet
- UP1 Add Math F5 2014Document15 pagesUP1 Add Math F5 2014Diana YusofNo ratings yet
- Sample Paper - 2012 Class - Xii Subject - Mathematics: Findab AndbDocument4 pagesSample Paper - 2012 Class - Xii Subject - Mathematics: Findab AndbakmxsafNo ratings yet
- Higher 2 Mathematics: Paper 1Document6 pagesHigher 2 Mathematics: Paper 1Seng SoonNo ratings yet
- Linear EquationDocument6 pagesLinear EquationTRIZIE CHENGNo ratings yet
- Eoc Practicews 5Document1 pageEoc Practicews 5api-241157101No ratings yet
- PersonalDocument8 pagesPersonalAtanu Brainless RoyNo ratings yet
- Kerja Cuti Sekolah Tahun Baru Cina MT Ting 4 2013Document2 pagesKerja Cuti Sekolah Tahun Baru Cina MT Ting 4 2013SohameddyNo ratings yet
- 1Document7 pages1SachinSharmaNo ratings yet
- Name: - Section: - ScoreDocument4 pagesName: - Section: - ScoreDina M. ValdoriaNo ratings yet
- MCR3U Exam Review 2013Document9 pagesMCR3U Exam Review 2013Hari MenonNo ratings yet
- NullDocument10 pagesNullapi-26004855No ratings yet
- Msqe Pea Peb 2015 PDFDocument10 pagesMsqe Pea Peb 2015 PDFsushant jhaNo ratings yet
- Handout 6 (Chapter 6) : Point Estimation: Unbiased Estimator: A Point EstimatorDocument9 pagesHandout 6 (Chapter 6) : Point Estimation: Unbiased Estimator: A Point EstimatoradditionalpylozNo ratings yet
- Handout - Measures of Central Tendencyt - GroupedDocument5 pagesHandout - Measures of Central Tendencyt - GroupedSyElfredGNo ratings yet
- Mathematics NAME: - SECTION: - A. EASY (2 Points Each)Document5 pagesMathematics NAME: - SECTION: - A. EASY (2 Points Each)Bryan MagnayeNo ratings yet
- C3 Differentiation - Implicit DifferentiationDocument3 pagesC3 Differentiation - Implicit DifferentiationDwi PradnyanaNo ratings yet
- Maths PMR Form 3 NotesDocument4 pagesMaths PMR Form 3 NotesAkashahNadiha MarsyaAmnaNo ratings yet
- HSC Trial 2021 Mathematics AdvancedDocument33 pagesHSC Trial 2021 Mathematics Advancedwill100% (1)
- DocumentDocument8 pagesDocumentmauryavks15No ratings yet
- Correction BTS 2023 Maths B1Document3 pagesCorrection BTS 2023 Maths B1LETUDIANTNo ratings yet
- Problem Sheet 10 Applications of DifferentiationDocument2 pagesProblem Sheet 10 Applications of Differentiationn0tsewNo ratings yet
- Y MX + C Is The Linear Equation of A Straight Line Y: y y y y or X X X XDocument12 pagesY MX + C Is The Linear Equation of A Straight Line Y: y y y y or X X X XLee Fhu SinNo ratings yet
- Pretest GenmathDocument3 pagesPretest GenmathHaruki AfkNo ratings yet
- Assessment Grade 11Document4 pagesAssessment Grade 11Shout Out DacanhighNo ratings yet
- CH 4 Linear Equation in One UnknownDocument2 pagesCH 4 Linear Equation in One UnknowneddiechowNo ratings yet
- Functions Review PacketDocument7 pagesFunctions Review Packetapi-267265141No ratings yet
- Form 4 Add Maths Final P2Document16 pagesForm 4 Add Maths Final P2Liew Kok YeeNo ratings yet
- Factoring and Algebra - A Selection of Classic Mathematical Articles Containing Examples and Exercises on the Subject of Algebra (Mathematics Series)From EverandFactoring and Algebra - A Selection of Classic Mathematical Articles Containing Examples and Exercises on the Subject of Algebra (Mathematics Series)No ratings yet
- Applications of Derivatives Errors and Approximation (Calculus) Mathematics Question BankFrom EverandApplications of Derivatives Errors and Approximation (Calculus) Mathematics Question BankNo ratings yet
- Differential Equations (Calculus) Mathematics E-Book For Public ExamsFrom EverandDifferential Equations (Calculus) Mathematics E-Book For Public ExamsRating: 5 out of 5 stars5/5 (1)
- OFF-LINE Registration Form: 3 International Conference On Microwave and Photonics (ICMAP) - 2018Document1 pageOFF-LINE Registration Form: 3 International Conference On Microwave and Photonics (ICMAP) - 2018avi0341No ratings yet
- Hash Functions: A Gentle Introduction: Palash SarkarDocument74 pagesHash Functions: A Gentle Introduction: Palash Sarkaravi0341No ratings yet
- At The Time of Admission or Latest by September 15, 2016Document1 pageAt The Time of Admission or Latest by September 15, 2016avi0341No ratings yet
- Cryptographic Hash FunctionsDocument55 pagesCryptographic Hash Functionsavi0341No ratings yet
- Role of Wickability On The Critical Heat Flux of Structured Superhydrophilic SurfacesDocument10 pagesRole of Wickability On The Critical Heat Flux of Structured Superhydrophilic Surfacesavi0341No ratings yet
- Notice M.tech. (MKM)Document1 pageNotice M.tech. (MKM)avi0341No ratings yet
- Studies On Cryptosystem by Applying Chaos: Avishek KumarDocument1 pageStudies On Cryptosystem by Applying Chaos: Avishek Kumaravi0341No ratings yet
- Motivation: 100584R - W.A.H.R.WeerathungeDocument2 pagesMotivation: 100584R - W.A.H.R.Weerathungeavi0341No ratings yet
- Department of Instrumention Science University of Pune List of JournalDocument2 pagesDepartment of Instrumention Science University of Pune List of Journalavi0341No ratings yet
- Energies: Battery Management Systems in Electric and Hybrid VehiclesDocument18 pagesEnergies: Battery Management Systems in Electric and Hybrid Vehiclesavi0341No ratings yet
- An Introduction To Cryptography and Digital Signatures: Author: Ian Curry March 2001Document6 pagesAn Introduction To Cryptography and Digital Signatures: Author: Ian Curry March 2001avi0341No ratings yet
- Shift-Tolerance Property of An Optical Double-Random Phase-Encoding Encryption SystemDocument7 pagesShift-Tolerance Property of An Optical Double-Random Phase-Encoding Encryption Systemavi0341No ratings yet
- Compressive Optical Image Encryption: Jun Li, Jiao Sheng Li, Yang Yang Pan & Rong LiDocument10 pagesCompressive Optical Image Encryption: Jun Li, Jiao Sheng Li, Yang Yang Pan & Rong Liavi0341No ratings yet
- El Gamal PDFDocument2 pagesEl Gamal PDFavi0341No ratings yet
- MidSem 2016Document2 pagesMidSem 2016avi0341No ratings yet
- HTCH QR$ S (F-/E-Mail: QffiffirDocument2 pagesHTCH QR$ S (F-/E-Mail: Qffiffiravi0341No ratings yet
- Rotary Club of Asansol: 3240 R I DistrictDocument4 pagesRotary Club of Asansol: 3240 R I Districtavi0341No ratings yet
- Hindi Poems and Motivation PDFDocument6 pagesHindi Poems and Motivation PDFavi0341No ratings yet
- Death Related EncountersDocument4 pagesDeath Related Encountersavi034167% (3)
- ReadMe PDFDocument2 pagesReadMe PDFavi0341No ratings yet
- Disentangling Classical and Bayesian Approaches To Uncertainty AnalysisDocument19 pagesDisentangling Classical and Bayesian Approaches To Uncertainty Analysiszilangamba_s4535No ratings yet
- PPSD A TT 027 0002 R0Document14 pagesPPSD A TT 027 0002 R0santosh_ms_kumar2827No ratings yet
- PADT TheFocus 35 PDFDocument18 pagesPADT TheFocus 35 PDFDipak BorsaikiaNo ratings yet
- Be & Ca PDFDocument45 pagesBe & Ca PDFRonimack Trajano de SouzaNo ratings yet
- TD12 CompleteDocument110 pagesTD12 Completemadina1386100% (2)
- Fabrication Layout Design Rules 2005Document28 pagesFabrication Layout Design Rules 2005lai_infoNo ratings yet
- Sulpiride MonographieDocument3 pagesSulpiride MonographieMohamed DahmaneNo ratings yet
- TRIAL STPM Mathematics M 2 (SABAH) SMK Tinggi KotaKinabaluDocument12 pagesTRIAL STPM Mathematics M 2 (SABAH) SMK Tinggi KotaKinabaluSKNo ratings yet
- Building Envelope Design Guide - Curtain Walls - Whole Building Design GuideDocument8 pagesBuilding Envelope Design Guide - Curtain Walls - Whole Building Design GuideAyman_Elmasry_9107No ratings yet
- Scope TC 9124Document1 pageScope TC 9124Esscon Engineering Services Pvt. Ltd.No ratings yet
- Preliminaries: Properties of IntegersDocument5 pagesPreliminaries: Properties of Integerssepti roichatul wardahNo ratings yet
- N Different Books (N 3) Are Put at Random in A Shelf. Among These Books There Is A ParticularDocument8 pagesN Different Books (N 3) Are Put at Random in A Shelf. Among These Books There Is A ParticularAnkit Gupta100% (1)
- Physics of Artificial GravityDocument15 pagesPhysics of Artificial GravityWilliam RiveraNo ratings yet
- White Paper Hydraulic Press Calculation-SflbDocument3 pagesWhite Paper Hydraulic Press Calculation-SflbHamam SuhailyNo ratings yet
- Dvp-Es2 Ss2 Sa2 Sx2-Program o en 20110302Document14 pagesDvp-Es2 Ss2 Sa2 Sx2-Program o en 20110302yasinNo ratings yet
- MICROECONOMICS ch07ANNEXDocument6 pagesMICROECONOMICS ch07ANNEXSabrina GoNo ratings yet
- Revent Us 723 Hirez 1Document2 pagesRevent Us 723 Hirez 1Umma NakhlunNo ratings yet
- 1.8 Rack Shift of The Gear: UndercutDocument6 pages1.8 Rack Shift of The Gear: UndercutJuanNo ratings yet
- Mills - CatalogDocument4 pagesMills - Catalogdéborah_rosalesNo ratings yet
- Datasheet BSS66Document1 pageDatasheet BSS66Diego DiazNo ratings yet
- 27-12-14 SR - Iit-Z (Iz) Co-Spark Jee Main (2011) Ptm-16 Q'paperDocument23 pages27-12-14 SR - Iit-Z (Iz) Co-Spark Jee Main (2011) Ptm-16 Q'paperazeemNo ratings yet
- Lecture 3-1: HFSS 3D Design Setup: Introduction To ANSYS HFSSDocument40 pagesLecture 3-1: HFSS 3D Design Setup: Introduction To ANSYS HFSSRicardo MichelinNo ratings yet
- Earth EvolutionDocument37 pagesEarth Evolutionkrish_mplNo ratings yet
- Ecoupled Understanding Wireless PowerDocument14 pagesEcoupled Understanding Wireless PowerLeon BurgerNo ratings yet
- Rays and RadiationsDocument43 pagesRays and RadiationsAnonymous SCZ4uYNo ratings yet
- 1 s2.0 S1359431199000496 Main PDFDocument14 pages1 s2.0 S1359431199000496 Main PDFWILLIAMCARABALINo ratings yet
- Radial Distribution Function For Argon Calculations From Thermodynamic Properties andDocument11 pagesRadial Distribution Function For Argon Calculations From Thermodynamic Properties andrafelNo ratings yet
- MDOT Research Report NMB Splice PDFDocument74 pagesMDOT Research Report NMB Splice PDFRajnikanth GedhadaNo ratings yet
- CG Industrial Product OverviewDocument12 pagesCG Industrial Product Overviewvanessa quispeNo ratings yet
- WEEK 5 Dot Product and WorkDocument10 pagesWEEK 5 Dot Product and Workmaria1345No ratings yet