EE42/100- Spring 2006 Problem Set6 - Solutions

1. (Reading Assignment)
Sections 6.2, 6.3, 6.6 and 6.8 of Chapter 6 as well as sections 11.1 and 11.2 of
Chapter 11: Hambley 3
rd
edition.


2. Problem 5.53

Since the reactance is negative, the load is capacitive
Power delivered is kW R I P
rms
d
5 . 22 100 ) 15 (
2 2

Reactive power is kVAR X I P
rms
r
25 . 11 ) 50 ( ) 15 (
2 2

Power factor is
( ) [ ] [ ] % 44 . 89 57 . 26 cos 5 . 0 tan cos tan cos ) cos(
1 1

1
]
1

,
_

d
r
f
P
P
P

3. Problem 5.56

First let us compute the rms current ) (
rms
I
A I
j
I
rms
8 . 36 71 . 52 . 52
2 1
30 2 220 50 2 240

+


Knowing the current ) (
rms
I , we can now compute the power for each source
(absorbed or delivered)
Power delivered by source A
kW I P
rms A
8 . 8 ) 71 . 52 50 cos( 240
KVAR I Q
rms A
42 . 0 ) 71 . 52 50 sin( 240

Power dissipated/absorbed by source B
kW I P
rms B
5 . 7 ) 71 . 52 30 cos( 220
KVAR I Q
rms B
1 . 3 ) 71 . 52 30 sin( 220

Power dissipated/absorbed by the resistor
kW R I P
rms
R
35 . 1 1 ) 8 . 36 (
2 2


Power dissipated/absorbed by the inductor
kVAR X I P
rms
r
7 . 2 ) 2 ( ) 8 . 36 (
2 2



4. Problem 5.68

We are asked to find the Thevenin and Norton of the circuit given:
After Zeroing the sources, we have:










Now we can compute the Thevenin impedance as follow:

4 2 43 . 63 472 . 4
5 / 1 10 / 1
1
j
j
Z
t
+
+

Using KCL to compute for the current flowing at the upper end of the current source
under open circuit conditions, we get:
5
5 10
45 100
+

j
V V
OC OC
, Solving for V
OC
, we get
80 . 93 56 . 62
OC t
V V
And 36 . 30 99 . 13
t
t
t
Z
V
I
Therefore, the Thevenin and Norton equivalences are given by:










The maximum power that this circuit can deliver to a load with complex
impedance is computed as follow:
load load rms load
Z I P

2


Given 4 2 j Z
load
and
+ +

+
80 . 93 64 . 15
4 2 4 2
80 . 93 56 . 62
j j Z Z
V
I
load t
t
load

W Z I P
load load rms load
6 . 244
2



10
5j Z
t
4j
2
36 . 30 99 . 13
2 4j
80 . 93 56 . 62
+
-
The maximum power that this circuit can deliver to a load with complex
impedance is computed as follow:
load load rms load
Z I P

2


Given 472 . 4
load load
R Z &
+ +

+
08 . 62 223 . 8
472 . 4 4 2
80 . 93 56 . 62
j Z Z
V
I
load t
t
load

W R I P
load load rms load
2 . 151
2







5. Problem 6.9

The phasors for the steady state input and output of this filter are given as follow:
25 2
in
V and 20 1
out
V
Therefore, the complex value of the filter transfer function at f=5,000Hz will be given
as:
45 5 . 0 ) 000 , 5 (
in
out
V
V
H



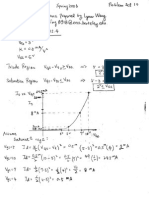
6. Problem 6.12

Given the input signal provided as
) 4000 cos( 4 ) 3000 sin( 3 ) 2000 cos( 2 1 ) ( t t t t V
in
+ + +
One can extract the following frequency components: 0, 1000, 1500 and 2000 Hz
The transfer function for each of these frequencies is compute by dividing the
corresponding output to the input. This results in the following:
3
1
3
) 0 ( H ,


30 2
0 2
30 4
) 000 , 1 ( H
, 90 1
90 3
0 3
) 500 , 1 (


H 0
0 4
0
) 000 , 2 (

H









7. Problem 6.19


Given the input signal to be ) 4000 cos( 4 ) 3000 sin( 3 ) 2000 cos( 2 1 ) ( t t t t V
in
+ + + with
frequencies components of 250, 500 and 1000 Hz
The half power of the filter frequency is Hz
RC
f
b
500
2
1

The transfer function is given by equation 6.9 in the text book
( )
b
f f
f H
+

1
1
) (
After computing the transfer function for the different component frequencies of
in
V , we
get the following:


+
57 . 26 89 . 0
)
500
250
( 1
1
) 250 (
j
H

+
45 707 . 0
)
500
500
( 1
1
) 500 (
j
H

+
43 . 63 44 . 0
)
500
1000
( 1
1
) 1000 (
j
H
Applying the appropriate value of the transfer function to each of these component of the
input signal allows us to an expression for the output signal which results to:
) 43 . 63 2000 cos( 236 . 2 ) 45 1000 cos( 535 . 3 ) 57 . 26 500 cos( 472 . 4 ) ( + + t t t t V
out




8. Problem 6.33


To convert to decibels, we need to take 20 times the common logarithm of a transfer
function. Therefore, we have:
dB 021 . 6 ) 5 . 0 log( 20 and dB 021 . 6 ) 2 log( 20 +