Journal of Sound and Vibration (1995) 182(3), 427440

NON-LINEAR VIBRATION OF CANTILEVER

SKEW PLATES SUBJECTED TO AERODYNAMIC
AND IN-PLANE EXCITING FORCES
T. H. YoiNc :Nb F. Y. CnrN
Department of Mechanical Engineering, National Taiwan Institute of Technology,
Taipei, Taiwan, R.O.C.
(Received 9 November 1993, and in nal form 28 February 1994)
A previous work of the authors shows that a cantilever skew plate acted upon by an
aerodynamic force and a small, slowly varying in-plane force may become unstable before
the aerodynamic force reaches its critical value. This paper describes a study of the
non-linear vibration of a cantilever skew plate when it becomes unstable. A nite element
formulation is rst applied to obtain the discretized system equations. The system equations
are then partially uncoupled and reduced in size by the modal truncation method. Finally,
the method of multiple scales is used to determine the response amplitudes of the plate.
The eects of the system parameters on the response of the plate are studied numerically.
1. INTRODUCTION
The stability of elastic structures exposed to air ows is one of the major considerations
in structural design, especially for aerospace structures where high speed air ow and a
low safety factor are encountered in design. Therefore, many references pertaining to this
topic can be found in the existing literature [14]. In most of the references the structures
are considered to be subjected to aerodynamic forces only and primarily with the
determination of the critical value of the aerodynamic pressure [57] is the objective.
It would be more general and physically realistic to consider simultaneously the in-plane
forces induced by edge constraints or thermal loadings. Dugundji [8] found the exact
solution for a simply supported rectangular plate subjected to aerodynamic and in-plane
forces. Numerical results show that the critical aerodynamic pressure increases with
increasing aerodynamic damping. The critical aerodynamic pressure of a quadrilateral
plate subjected simultaneously to in-plane loads was calculated by Sander, Bon and
Geradin [9] by using conforming and non-conforming nite elements. Convergence studies
for these two kinds of elements and the eects of aspect ratio, ow angularity and in-plane
loads are presented in this work, and the calculated results are also compared with
experimental ones. Kariappa, Somashekar and Shah [10] applied the matrix displacement
method to solve the utter problem of a skew panel with in-plane forces under a yawed
supersonic ow. The eects of the skew angle, yaw angle and in-plane force on the utter
boundaries of the skew panel were studied.
The post-utter behavior of panels has also attracted researchers attention in the past
few decades. Dowell [11] investigated the eects of system parameters on the post-utter
behavior of simply supported plates simultaneously subjected to both a supersonic
aerodynamic pressure and an in-plane force. Galerkins method was used in this work to
eliminate the dependence on the spatial co-ordinates, yielding a set of non-linear ordinary
427
0022460X/95/180427 +14 $08.00/0 7 1995 Academic Press Limited
1. n. .oiNc :Nb r. .. cnrN 428
dierential equations which was then solved by numerical integration. The non-linear
utter problem of rectangular plates acted upon by aerodynamic and mid-plane forces was
studied by Kuo, Morino and Dugundji [12]. Perturbation methods were applied to obtain
post-utter amplitudes of the plates. They found that the eect of the viscoelastic structural
damping on the utter boundaries was generally destabilizing, and the post-utter
behavior became more explosive. Non-linear panel utter problems were also studied by
Mei [13] and by Han and Yang [14] by the nite element method. The static in-plane
loadings were included in both works.
The in-plane force considered in the above references is static. However, in real
situations, it is usually time-dependent. Young and Chen [15] rst studied the stability of
skew panels subjected to both an aerodynamic pressure and a small, slowly varying
in-plane force simultaneously. The authors found that due to this small, slowly varying
force, the panel may become unstable before the aerodynamic force reaches its critical
value. In what follows here the past eort is extended further to investigate the non-linear
vibration of the same panel when it becomes unstable.
2. EQUATION OF MOTION
A cantilever skew plate of side lengths a and b and of uniform thickness h with a skew
angle u, subjected to both aerodynamic and in-plane forces, is shown in Figure 1. In this
gure, the relations between the skew co-ordinates (z
1
, z
2
) and the Cartesian co-ordinates
(x
1
, x
2
) are given by
z
1
=x
1
x
2
tan u, z
2
=x
2
/cos u. (1)
According to the von Ka rma n plate theory, the bending strain energy takes the form [16]
U
b
=
1
2
g
V
e
T
[E]e dV, (2)
where V is the volume of the plate, e
T
is the transpose of the column matrix of the strain
components, and [E] is the material-property matrix: i.e.,
e
T
=
8
u
1,1
+u
2
3,1
u
2,2
+u
2
3,2
u
1,2
+u
2,1
+u
3,1
u
3,29
x
3
8
u
3,11
u
3,22
2u
3,129
, [E] =
E
1 n
2
&
1
n
0
n
1
0
0
0
(1 n)/2
'
,
where u
i
are the displacement components of the plate, and a comma denotes partial
dierentiation with respect to the following x
i
. E and n are the Youngs modulus and the
Figure 1. The conguration of a cantilever skew plate subjected to both an aerodynamic and an in-plane
exciting force.
sirv ii:1r vi1n :rro :Nb iN-ii:Nr rorcrs 429
Poisson ratio of the plate, respectively. According to the Kirchho hypothesis, the shear
deformation is neglected in the bending strain energy. Consistent with this hypothesis, the
rotary inertia is also omitted in the kinetic energy. Therefore, the kinetic energy of the plate
can be written as
T=
rh
2
g
A
(u
3
)
2
dA, (3)
where r and A are the mass density and the area of the plate, respectively. The dot denotes
partial dierentiation with respect to time t.
The aerodynamic pressure for a suciently high supersonic ow can be described by
two-dimensional rst order theory (also called piston theory) as [17]
p(z
1
, z
2
, t) =
2q
zM
2
a
1 0
1u
3
1z
2
+
u
3
U
M
2
a
2
M
2
a
1
1
, (4)
where q is the dynamic pressure, M
a
is the Mach number, and U is the ow velocity.
Therefore, the virtual work done by the aerodynamic force is expressed as
dW
a
=
g
A
p(z
1
, z
2
, t) du
3
dA. (5)
The virtual work done by the in-plane force is [16]
dW
p
=
g
G
f (t) du
1
dG, (6)
in which G is the boundary where the in-plane force is applied. Substituting the strain
energy, the kinetic energy and the virtual work done by the aerodynamic and in-plane
forces, as given by equations (2)(6), into Hamiltons principle and going through
variational manipulations yields the governing equation and the boundary conditions of
the system.
Since the problem possesses no exact solutions, no attempt is made in this work to obtain
the governing equation. Alternatively, approximate methods are utilized to nd an
approximate solution instead. The nite element method is used rst, to deal with the
dependence on the spatial co-ordinates. By the use of the three-node triangular CZK
element [18], the displacement within an element can be written as
8
u
1
u
2
u
39
=[N]a
e
, (7)
where a
e
and [N] are the nodal parameter vector and shape function matrix, respectively.
The nodal parameters for the ith node are divided into the in-plane and transverse
parameters, respectively: i.e.,
a
i
=
6
a
p
i
a
b
i 7
with a
p
i
=
6
u
1i
u
2i 7
and a
b
i
=
8
u
3i
hu
3,1i
hu
3,2i 9
, i =1, 2, 3.
The shape function matrix for the ith element can also be subdivided as
[N
i
] =
$
[N
p
i
]
[0]
[0]
[N
b
i
]
%
,
where [N
p
i
] and [N
b
i
] are 2 6 and 1 9 matrices, respectively, and are given in the book
of Zienkiewicz [18].
1. n. .oiNc :Nb r. .. cnrN 430
By the standard nite element formulation, the following equations for the discretized
system are obtained:
[K
11
]j +[K
12
]h +K
u
(z) =(ah/D)f(t)F
p
, [K
21
]j +[K
22
]h +K
v
(z) =0, (8a, b)
(rha
4
/D)[M]z+(ma
4
/D)[C]z +[K
b
]z +(ba
3
/D)[F
a
]z +K
w
(j, h, z) =0. (8c)
Here b =2q/zM
2
a
1, m =(b/U)[(M
2
a
2)/(M
2
a
1)], j =u
1
/h, h =u
2
/h and z =a
b
/h,
in which u
1
, u
2
and a
b
are formed by u
1i
, u
2i
and a
b
i
. In equations (8), [K
11
], [K
12
], [K
21
] and
[K
22
] are membrane stiness matrices. [M], [C], and [K
b
] are the mass, damping and
bending stiness matrices, respectively. K
u
and K
v
are vectors and are functions of z, while
K
w
is a function of j, h and z. F
p
is a vector due to the in-plane force, and [F
a
] is a matrix
due to the aerodynamic force. From equations (8a) and (8b), j and h can be expressed
in terms of z, and equation (8c) can be written as
(rha
4
/D)[M]z +(ma
4
/D)[C]z +[K
b
]z +(ba
3
/D)[F
a
]z +(a
2
/D) f (t)[F
p
]z +[K
n
(z)]z =0,
(9)
where [F
p
] is a matrix due to the in-plane force, and [K
n
(z)] is a matrix of which the entries
are quadratic functions of z. Note that the damping matrix [C] is equal to the mass matrix
[M]; the matrices [M], [K
b
] and [F
p
] are symmetric, while [F
a
] is asymmetric.
Equation (9) is a set of non-linear dierential equations with variable coecients and
cannot be solved exactly. To improve the solvability of the system equations, a modal
analysis procedure is applied to decouple the linear autonomous terms in the equations.
The procedure can be stated briey as follows. By considering the corresponding
undamped, linear autonomous system equations and letting z =ye
ivt
gives the following
eigenvalue problem:
(rha
4
v
2
/D)[M]y ([K
b
] +(ba
3
/D)[F
a
])y =0. (10)
This eigenvalue problem can be solved for all natural frequencies v and right modal
vectors y. For small values of b, the natural frequencies are all real and distinct. As the
value of b reaches a specic value, two of the natural frequencies become equal, and the
system is said to be uttered. This specic value of b is called the critical aerodynamic
pressure (denoted b
cr
). In this work, the aerodynamic pressure parameter b is assumed to
be smaller than its critical value b
cr
. Since [F
a
] is asymmetric, to decouple it, one needs
to solve the adjoint eigenvalue problem of equation (10), i.e.,
(rha
4
v
2
/D)z
T
[M] z
T
([K
b
] +(ba
3
/D)[F
a
]) =0, (11)
where v are again the natural frequencies of the same system, and z are the left modal
vectors of the system. If the modal vectors are normalized with respect to the mass matrix,
i.e., [Z]
T
[M][Y] =[I], then [Z]
T
([K
b
] +(ba
3
/D)[F
a
])[Y] =[rha
4
v
2
/D], where [Y] and [Z] are
the right and left modal matrices, respectively, [I] is an identity matrix, and [rha
4
v
2
/D] is
a diagonal matrix with each diagonal entry being the square of the nondimensional natural
frequencies.
Usually, utter occurs among the lowest few modes, and one has to deal with these
modes only. Therefore, the size of the system equations should be reduced in order to save
storage space and computing time. One thus can introduce a linear transformation
z =[Y]v, where [Y] is a truncated right modal matrix formed by the rst M normalized
modes. Substituting this transformation into equation (9), premultiplying the transpose of
the corresponding truncated left modal matrix [Z]
T
to the equation and making use of the
sirv ii:1r vi1n :rro :Nb iN-ii:Nr rorcrs 431
orthogonality of the modal vectors yields the reduced and partially uncoupled form of
equation (9),
(rha
4
/D)v +(ma
4
/D)v +[ rha
4
v
2
/D]v +(f (t)a
2
/D)[G]v +[K
n
(v)]v =0, (12)
where the matrices [G] =[Z]
T
[F
p
][Y] and [K
n
] =[Z]
T
[K
n
(v)][Y]. The (ij)th entry of [K
n
(v)]
has the form k
ij
=v
T
[Z]
T
[H]
ij
[Y]v, where [H]
ij
is a constant matrix.
The system equations (12) still cannot be solved exactly. If the non-linear and the
non-autonomous terms are small in comparison with the others, the system is said to be
weakly non-linear and weakly non-autonomous, and perturbation methods can be used
to construct analytical solutions of the system.
3. PERTURBATION ANALYSIS
The in-plane force f(t) is assumed to be periodic. Therefore, it can be expressed in a
Fourier series of the form
f (t) = s
J
j =J
f
j
e
ijVt
, (13)
where V is called the fundamental excitation frequency. Since the in-plane force is assumed
to be small compared to the aerodynamic force ba, the magnitude of each Fourier
coecient f
j
is also small compared to ba. Therefore, the small parameter e appearing in
the perturbation technique is dened as e == f
J
=/b
cr
a. In addition, the temporal variable is
changed so that the dierential equation is in terms of the dimensionless variable
t =zD/rha
4t
. This change transforms equation (12) into the form
v0
m
(t) +2av'
m
(t) +v
2
m
v
m
(t) +e s
J
j =J
f
j
e
iV

j
t
s
M
n =1
g
mn
v
n
(t) + s
M
n =1
s
M
r =1
s
M
s =1
k
mnrs
v
n
v
r
v
s
=0,
m=1, . . . , M, (14)
where v
m
and g
mn
are entries of the matrices v and [G], respectively; k
mnrs
is the (rs)th entry
of the matrix [H]
mn
. A prime denotes a dierentiation with respect to t, and
a =ma
2
/2zrhD, f
j
=f
j
b
cr
a
3
/= f
J
=D, v
m
=v
m
zrha
4
/D and V
j
=jVzrha
4
/D.
The method of multiple scales can be used to nd an analytical solution of equation
(14). One begins by introducing new independent variables T
k
as dened in the textbook
by Nayfeh and Mook [19]. It follows that the derivatives with respect to t become
expressions in terms of the partial derivatives with respect to T
k
of the form
d
dt
=
dT
0
dt
1
1T
0
+
dT
1
dt
1
1T
1
+ =D
0
+eD
1
+ ,
d
2
dt
2
=D
2
0
+2eD
0
D
1
+ . (15)
It is assumed that the solution of equation (14) can be represented by a uniformly valid
expansion having the form
v
m
(t, e) =v
m0
(T
0
, T
1
. . . ) +ev
m1
(T
0
, T
1
. . . ) + . (16)
The expansion is carried out to the order of e
2
here; therefore, only T
0
and T
1
are necessary.
Substituting equations (15) and (16) into equation (14) and equating the coecients of like
powers of e yields the equations:
order 1, D
2
0
v
m0
+v
2
m
v
m0
=0; (17)
1. n. .oiNc :Nb r. .. cnrN 432
order e, D
2
0
v
m1
+v
2
m
v
m1
=2D
0
(D
1
+a)v
m0
s
J
j =J
f
j
e
iV
j
T
0
s
M
n =1
g
mn
v
n0
s
M
n =1
s
M
r =1
s
M
s =1
k
mnrs
v
n0
v
r0
v
s0
, (18)
where a =ea and k
mnrs
=ek
mnrs
are assumed in order to have the damping and the non-linear
terms appearing in the same order as the rst non-autonomous term.
The general solution of equation (17) is found to be
v
m0
=H
m
(T
1
) e
iv
m
T
0
+c.c., (19)
where c.c. denotes the complex conjugate of the preceding term, and H
m
is an
undetermined function of T
1
. Substituting equation (19) into equation (18) gives
D
2
0
v
m1
+v
2
m
v
m1
=2iv
m
(D
1
H
m
+aH
m
) e
iv
m
T
0
s
J
j =1
s
M
n =1
f
j
g
mn
[H
n
e
i(V
j
+v
n
)T
0
+H
n
e
i(V
j
v
n
)T
0
] s
M
n =1
s
M
r =1
s
M
s =1
k
mnrs
[H
n
H
r
H
s
e
i(v
n
+v
r
+v
s
)T
0
+H
n
H
r
H
s
e
i(v
n
v
r
+v
s
)T
0
+H
n
H
r
H
s
e
i(v
n
+v
r
v
s
)T
0
+H
n
H
r
H
s
e
i(v
n
v
r
v
s
)T
0
] +c.c., (20)
where H
m
denotes the complex conjugate of H
m
, and f
0
is assumed to be zero without loss
of generality. To this order of approximation, there exist three possible frequency
combinations of V
j
, v
p
and v
q
. All three cases of frequency combinations will be
investigated separately in the following:
3.1. 1nr c:sr or V
j
:v:. rrox v
p
2v
q
When the frequency of the excitation is away from the sum or the dierence of two
natural frequencies of the system, one speaks of a non-resonant case. In this case, to obtain
a periodic solution, the secular termsterms with e
iv
m
T
0
must be eliminated from
equation (20), which yields
H
m
=h
m
e
aT
1
, (21)
where h
m
is an undetermined coecient. Now v
m1
can be obtained from equation (20) as
v
m1
= s
J
j =1
s
M
n =1
f
j
g
mn
$
H
n
(V
j
+v
n
)
2
v
2
m
e
i(V
j
+v
n
)T
0
+
H
n
(V
j
v
n
)
2
v
2
m
e
i(V
j
v
n
)T
0
%
+c.c. +N.L.T., (22)
where N.L.T. denotes non-linear terms of H
m
. Since H
m
will die out as time passes, the
system is always stable in this case.
3.2. 1nr c:sr or V
j
Nr:r v
p
v
q
When the frequency of the excitation is close to the dierence of two natural frequencies
of the system, combination resonance of the dierence type exists between the pth and qth
modes. First, a detuning parameter s, which quantitatively describes the nearness of V

j
to v
p
v
q
is introduced according to
V
j
=v
p
v
q
+es. (23)
sirv ii:1r vi1n :rro :Nb iN-ii:Nr rorcrs 433
This has the advantage of helping one to recognize the terms that lead to secular terms.
Then, setting the coecients of these terms to zero in equation (20) yields
2iv
p
(D
1
+a)H
p
+f
j
g
pq
H
q
e
isT
1
+3k
pppp
H
2
p
H
p
+2 s
M
n =1,n $p
(k
pnnp
+k
pnpn
+k
ppnn
)H
n
H
n
H
p
=0, (24a)
2iv
q
(D
1
+a)H
q
+f
j
g
qp
H
p
e
isT
1
+3k
qqqq
H
2
q
H
q
+2 s
M
n =1,n $q
(k
qnnq
+k
qnqn
+k
qqnn
)H
n
H
n
H
q
=0, (24b)
2iv
m
(D
1
+a)H
m
+3k
mmmm
H
2
m
H
m
+2 s
M
n =1,n $m
(k
mnnm
+k
mnmn
+k
mmnn
)H
n
H
n
H
m
=0,m$p or q. (24c)
One assumes that the solution of equations (24) has the form
H
m
=h
m
e
iu
m
, m=1, 2 . . . , M, (25)
where h
m
and u
m
are real functions of T
1
. Substituting H
m
in this form into equation (24)
and separating the real and imaginary parts yields the equations
2v
p
h
p
u'
p
+f
j
g
pq
h
q
cos g +3k
pppp
h
3
p
+2 s
n =1,n $p
(k
ppnn
+k
pnpn
+k
pnnp
)h
2
n
h
p
=0, (26a)
2v
p
h'
p
+2av
p
h
p
+f
j
g
pq
h
q
sin g =0, (26b)
2v
q
h
q
u'
q
+f
j
g
qp
h
p
cos g +3k
qqqq
h
3
q
+2 s
n =1,n $q
(k
qqnn
+k
qnqn
+k
qnnq
)h
2
n
h
q
=0, (26c)
2v
q
h'
q
+2av
q
h
q
f
j
g
qp
h
p
sin g =0, (26d)
2v
m
h
m
u'
m
+3k
qqqq
h
3
q
+2 s
n =1,n $m
(k
mmnn
+k
mnmn
+k
mnnm
)h
2
n
h
m
=0, (26e)
2v
m
h'
m
+2av
m
h
m
=0, (26f)
where g =sT
1
+u
q
u
p
. From equation (26f), h
n
, if n is not equal to p and q, is found
to be
h
n
=S
n
e
aT
1
, (27)
where S
n
is an integration constant. As T
1
approaches innity, h
n
will decay to zero if n
is not equal to p and q: that is, for steady state vibration, h
n
will not be present. Moreover,
h'
p
, h'
q
and g' are all equal to zero for steady state vibration, and equations (26a)(26d)
can be reduced to
2v
p
v
q
h
p
h
q
s +f
j
(g
pq
v
q
h
2
q
g
pq
v
q
h
2
q
) cos g +(C
p
h
2
p
C
q
h
2
q
)h
p
h
q
=0, (28a)
2av
p
h
p
+f
j
g
pq
h
q
sin g =0, 2av
q
h
q
f
j
g
qp
h
p
sin g =0, (28b, c)
where
C
p
=3k
pppp
v
q
2v
p
(k
qqpp
+k
qpqp
+k
qppq
)
and
C
q
=3k
qqqq
v
p
2v
q
(k
ppqq
+k
pqpq
+k
pqqp
).
1. n. .oiNc :Nb r. .. cnrN 434
If h
p
and h
q
are not equal to zero simultaneously, from equations (28b) and (28c), the
following relations exist:
sin g =z4a
2
v
p
v
q
/f
2
j
g
pq
g
qp
, h
p
=zv
q
g
pq
/v
p
g
qp
h
q
. (29a, b)
Note that if g
pq
and g
qp
have opposite signs, a dierence type of combination resonance
between the pth and qth modes exists; otherwise, it does not exist. Substituting the above
expressions into equation (28a) gives the response amplitudes:
h
p
=
6
2v
p
v
q
s 22zv
p
v
q
(f
2
j
g
pq
g
qp
4a
2
v
p
v
q
)
C
p
+C
q
v
p
g
qp
/v
q
g
pq 7
1/2
. (30)
Note that letting h
p
equal zero yields the expression for the transition curves, the curves
which separate stable solutions from unstable ones, of the system:
V
j
=v
p
v
q
2ezf
2
j
g
pq
g
qp
/v
p
v
q
4a
2
. (31)
This expression coincides with that given in the previous work by the authors [15].
Equation (30) gives two sets of steady state solutions, one of which is stable while the
other is unstable. By investigating the nature of the singular points of equations (26), the
stability of the steady state motion can be determined. Let the solutions of these equations
be
h
p
=h
0
p
+h*
p
, h
q
=h
0
q
+h*
q
, g =g
0
+g*,
h
n
=h*
n
n $p, n $q, u
n
=u*
n
n $p, n $q, (32)
h
0
p
, h
0
q
and g
0
being the steady state solutions of the system. Substituting the assumed
solutions into equations (26), expanding for small variations h*
p
, h*
q
, g*, h*
n
and u*
n
, noting
that the steady state solutions satisfy equations (28), and keeping the terms linear in the
small variations yields
d =[A]d, (33)
where [A] is a constant matrix, and d =[h*
p
, h*
q
, g*, h*
n
, u*
n
]
T
. Upon assuming that
d =de
lT
1
, equation (33) becomes an eigenvalue problem. If the real parts of all eigenvalues
l are negative, the steady state solutions are stable. Otherwise, they are unstable.
3.3. 1nr c:sr or V
j
Nr:r v
p
+v
q
When the frequency of the excitation is close to the sum of two natural frequencies of
the system, combination resonance of the summed type exists between the pth and qth
modes. Again, one introduces a detuning parameter s such that
V
j
=v
p
+v
q
+es, (34)
and, by following the above-stated procedure, the response amplitudes may be obtained
from equations (29b) and (30) by changing the sign of v
q
, as
h
p
=
6
2v
p
v
q
s 22zv
p
v
q
(f
2
j
g
pq
g
qp
4a
2
v
p
v
q
)
C
p
+C
q
v
p
g
qp
/v
q
g
pq 7
1/2
, p $q, (35a)
and
h
q
=zv
p
g
qp
/v
q
g
pq
h
p
, (35b)
sirv ii:1r vi1n :rro :Nb iN-ii:Nr rorcrs 435
where C
p
=3k
pppp
v
q
+2v
p
(k
qqpp
+k
qpqp
+k
qppq
) and C
q
=3k
qqqq
v
p
+2v
q
(k
ppqq
+k
pqpq
+
k
pqqp
). Again, the transition curves corresponding to this type of combination resonances
can be found by letting h
p
equal zero, which yields
V
j
=v
p
+v
q
2ezf
2
j
g
pq
g
qp
/v
p
v
q
4a
2
. (36)
When p is equal to q, one speaks of main resonances. In this case, the response amplitudes
and the transition curves are given by
h
p
=
6
v
p
s 2zf
2
j
g
2
pp
4a
2
v
2
p
3k
pppp 7
1/2
, V
j
=2v
p
+ezf
2
j
g
2
pp
/v
2
p
4a
2
. (37a, b)
Note that although the expression for the transition curves at main resonances can be
obtained from that of a combination resonance of the summed type, equation (36), by
letting p equal q, the expression for the response amplitudes at such resonances cannot
be so obtained from equation (35a).
4. NUMERICAL RESULTS AND DISCUSSION
As an example of application of the general solutions, the in-plane force is assumed to
be a simple harmonic function, i.e., f(t) =F
0
cos Vt, where F
0
is assumed to be small
compared to b
cr
a. Hence the small parameter e appearing in the perturbation technique
is dened as e =F
0
/b
cr
a. Moreover, based on previous research experience of the authors
[15] with convergence of the numerical results, 72 elements with 126 degrees of freedom
in the transverse direction are used in the nite element discretization, and the number of
modes used in the modal truncation method is taken as 30.
The transition curves of a cantilever square plate subjected to a subcritical aerodynamic
pressure b/b
cr
=095 and an in-plane force are presented in Figure 2. This gure shows
that unstable regions are developed at V1v
2
v
1
, 2v
1
and 2v
2
but not at V1v
1
+v
2
,
and the unstable region at the second main resonance is larger than that at the rst one.
In addition, a larger value of the aerodynamic damping coecient causes all unstable
regions to shrink upwards. Therefore, the eect of the aerodynamic damping is stabilizing,
which coincides with the prediction of equations (31), (36) and (37b).
Since the eects of system parameters on the changes of the transition curves of the plate
have been studied in detail in the previous work by the authors [15], we will concentrate
our eort here on the changes of response amplitudes subjected to variations of the system
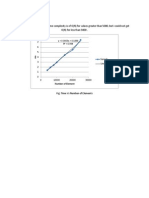
parameters in the present work. The response curves of the square plate considered in the
above gure with a small in-plane force (e =001) are shown in Figure 3. In this gure,
Figure 2. The transition curves of a cantilever square plate subjected to a subcritical aerodynamic pressure
and in-plane force: n =03 and b/bcr =095. , a=005; , a =01.
1. n. .oiNc :Nb r. .. cnrN 436
Figure 3. The response curves of a cantilever square plate subjected to a subcritical aerodynamic pressure and
an in-plane force: n =03, a =0.05, b/bcr =095 and e =001. (a) V1v2 v1; (b) V12v1; (c) V12v2.
one observes that only the right mode is excited at a main resonance, but two
corresponding modes are excited at a combination resonance. At these resonances, there
appear two response curves for each mode. The curve with a larger amplitude corresponds
to stable response, while the other one corresponds to unstable response. The points in
the gure represent the amplitudes of the limit circles obtained by numerical integration.
It is found that these points agree excellently with the stable response curves.
In Figure 3, the response curves at the rst main resonance lean toward the lower
frequency range and exhibit a soft-spring type of non-linearity despite large amplitude
vibration. This is because the value of k
1111
in equation (37a) is negative. However, the
curves at the second main resonance lean in the opposite direction and exhibit a hard-spring
type of non-linearity, since the value of k
2222
is positive. Due to the eect of the second mode,
the response curves at V1v
2
v
1
also exhibit a hard-spring type of non-linearity.
Furthermore, the amplitude of the rst mode is smaller than that of the second mode at
the dierence type of combination resonance V1v
2
v
1
because, according to equation
(29b), the amplitude ratio h
2
/h
1
depends not only on the frequency ratio v
1
/v
2
but also on
the ratio of the corresponding entries of the excitation matrix g
21
/g
12
.
From previous results, one nds that utter rst occurs at the coalescence of the rst
two natural frequencies for a cantilever square plate. Moreover, in this work, we are
interested in how a slowly varying in-plane force aects the dynamic behavior of the plate
when subjected simultaneously to a subcritical aerodynamic force. Therefore, we will focus
our attention on the response amplitudes at the dierence type of combination resonance
V1v
2
v
1
hereafter. The eect of the aerodynamic force on the response curves of the
cantilever square plate at V1v
2
v
1
is depicted in Figure 4. The gure shows that an
increase in the value of b/b
cr
results in smaller response amplitudes and in further
separation of each pair of the response curves. This means that the eect of the
aerodynamic force widens the unstable region in the linear analysis but reduces the
response amplitudes in the nonlinear analysis. Similar phenomena exist at the rst two
main resonances.
sirv ii:1r vi1n :rro :Nb iN-ii:Nr rorcrs 437
Figure 4. The response curves at V1v2 v1 of a cantilever square plate subjected to subcritical aerodynamic
and in-plane forces at dierent values of b/bcr : n =03, a =005 and e =001. (a) b/bcr =093; (b) b/bcr =095;
(c) b/bcr =097.
It is shown in Figure 3 that at each resonance, two response curves appear for each
mode. The one drawn by a solid line corresponds to stable response, while the other one
is unstable. Comparing with Figure 2, one nds that the left branch of the transition curve
at V1v
2
v
1
corresponds to a stable conguration, while the right branch corresponds
to an unstable conguration. The response curves at excitation frequencies below and
above the dierence of the rst two natural frequencies, respectively are illustrated in
Figure 5. In Figure 5(a), the excitation frequency is below the dierence of the rst
two natural frequencies. As the excitation amplitude increases from zero, the response
Figure 5. The response curves of a cantilever square plate subjected to subcritical aerodynamic and in-plane
forces at dierent frequencies: n =03, a =005 and b/bcr =095. (a) Vzrha
4
/D=14; (b) Vzrha
4
/D=16.
1. n. .oiNc :Nb r. .. cnrN 438
Figure 6. The response curves at V1v2 v1 of a cantilever square plate subjected to subcritical aerodynamic
and in-plane forces at dierent amplitudes: n =03, a =005 and b/bcr =095. (a) e =001; (b) e =002.
conguration will meet and cross the left branch of the transition curve in Figure 2, and the
response amplitudes will rise continuously from zero and increase steadily. In Figure 5(b),
the excitation frequency is above the dierence of the rst two natural frequencies. As the
excitation amplitude increases from zero, the response conguration will meet and cross
the right branch of the transition curve, and the response amplitudes are rst zero, then
jump vertically to the stable conguration at e =00032, and increase steadily afterwards.
The eect of the excitation amplitude on the response of the cantilever square plate (i.e.,
u =0) is shown in Figure 6. The gure reveals that a larger excitation amplitude results
Figure 7. The response curves at V1v2 v1 of a cantilever skew plate subjected to subcritical aerodynamic
and in-plane forces at dierent skew angles: a/b =10, n =03, a =005, b/bcr =095 and e =001. (a) u =0;
(b) u =15; (c) u =30.
sirv ii:1r vi1n :rro :Nb iN-ii:Nr rorcrs 439
in larger response amplitudes and causes the pair of response curves to separate from each
other. A greater distance between the pair of response curves corresponds a wider unstable
region. Therefore, the eect of the excitation amplitude is destablizing in both linear and
non-linear analyses.
The eect of changes of the skew angle on the response of a cantilever skew plate
subjected to both a subcritical aerodynamic pressure and an in-plane force is presented
in Figure 7. One nds from the gure that an increase in the skew angle causes the
pair of response curves to move closer together but results in larger response
amplitudes. herefore, the eect of the skew angle is stabilizing in the linear analysis, but
is unfavorable in the non-linear oscillation. Similar phenomena appear at the rst two main
resonances.
5. CONCLUSIONS
A previous research study showed that a skew plate subjected to a subcritical
aerodynamic force might become unstable when also under the action of a small, slowly
varying in-plane force. The dynamic response of such a skew plate was studied in the
present paper when it became unstable. Combination resonances of both the dierence and
summed types were shown to arise in the non-resonant solutions due to the
time-dependence of the in-plane force. Resonant solutions were then derived from which
the response amplitudes of the corresponding modes were obtained. Due to the complexity
of the problem, a simple harmonic function f(t) =F
0
cos Vt was considered to provide
numerical examples of the derived general solutions. However, solutions for more general
periodic functions can easily be generated for the rst few approximations.
From the numerical results, one obtains conclusions as follows. At all resonances, there
exist two response curves for each mode. The curve with a larger amplitude corresponds
to a stable conguration of the plate, while the other one is unstable. The response curves
may exhibit either a soft- or a hard-spring type of non-linearity, despite the large amplitude
vibration, but depending upon the characteristics of that mode at main resonances and
of the higher mode at combination resonances. The eect of the aerodynamic damping
is stabilizing, but the eect of the amplitude of the in-plane exciting force is destabilizing.
Moreover, an increase in the aerodynamic pressure widens the unstable regions in the
linear analysis but reduces the response amplitudes in the nonlinear analysis. An increase
in the skew angle shows the opposite trend.
REFERENCES
1. Y. C. FiNc 1960 A Summary of the Theories and Experiments on Panel Flutter. AFOSR TN
60224, California Institute of Technology, Pasadena, California.
2. Y. C. FiNc 1963 American Institute of Aeronautics and Astronautics Journal 1, 898909. Some
recent contributions to panel utter research.
3. E. H. Dovrii 1970 American Institute of Aeronautics and Astronautics Journal 8, 385399.
A review of the aeroelastic stability of plate and shell.
4. E. H. Dovrii 1975 Aeroelasticity of Plates and Shells. Leyden: Noordho.
5. S. Dirv:sii: 1967 American Institute of Aeronautics and Astronautics Journal 5, 16681673.
Flutter of simply supported, parallelogrammic, at panels in supersonic ow.
6. R. S. SriNiv:s:N and B. J. C. B:ni 1985 Journal of Sound and Vibration 98, 4553. Flutter
analysis of cantilevered quadrilateral plates.
7. M. D. OisoN 1970 American Institute of Aeronautics and Astronautics Journal 8, 747752. Flutter
solutions using nite elements.
8. J. DiciNbi 1966 American Institute of Aeronautics and Astronautics Journal 4, 12571266.
Theoretical considerations of panel utter at high supersonic Mach numbers.
1. n. .oiNc :Nb r. .. cnrN 440
9. G. S:Nbrr, C. BoN and M. Grr:biN 1973 Journal of Numerical Methods in Engineering 7,
379394. Finite element analysis of supersonic panel utter.
10. K:ri:ii:, B. R. Sox:snri:r and C. G. Sn:n 1970 American Institute of Aeronautics and
Astronautics Journal 8, 20172022. Discrete element approach to utter of skew panels with
in-plane forces under yawed supersonic ow.
11. E. H. Dovrii 1966 American Institute of Aeronautics and Astronautics Journal 4, 12671275.
Nonlinear oscillations of a uttering plate.
12. L. C. Kio, L. MoriNo and J. DiciNbi 1972 American Institute of Aeronautics and Astronautics
Journal 10, 14791484. Perturbation and harmonic balance methods for nonlinear panel utter.
13. C. Mri 1977 American Institute of Aeronautics and Astronautics Journal 15, 11071110. A nite
element approach for nonlinear panel utter.
14. A. D. H:N and T. Y. Y:Nc 1983 American Institute of Aeronautics and Astronautics Journal
21, 14531461. Nonlinear panel utter using high-order triangular nite element.
15. T. H. YoiNc and F. Y. CnrN 1994 Journal of Sound and Vibration 1994 171, 603615. Stability
of skew plates subjected to aerodynamic and in-plane forces.
16. A. W. Lriss: 1969 Vibration of Plates (NASA SP-160). Washington, D.C.: U.S. Government
Printing Oce.
17. R. L. BisiiiNcnorr and H. Asnir. 1962 Principles of Aeroelasticity. New York: John Wiley.
18. O. C. ZirNiirvicz 1977 The Finite Element Method. Maidenhead, Berkshire: McGraw-Hill.
19. A. H. N:.rrn and D. T. Mooi 1979 Nonlinear Oscillations. New York: John Wiley.