Maxima and Minima

1. Find all critical points of f(x, y) = x

2
+ y
2
.
Solution. We want f
x
= f
y
= 0. We calculate f
x
= 2x, f
y
= 2y , and the only way that this can be
true is for x and y to both be 0. Thus, the only critical point is (x, y) = (0, 0) .
2. Find all critical points of f(x, y) = 5 x
3
+ y
3
+ 3xy.
Solution. We want f
x
= f
y
= 0, and we can calculate f
x
= 3x
2
+ 3y, f
y
= 3y
2
+ 3x. So, we want
3x
2
+3y = 0 and 3y
2
+3x = 0. The rst equation tells us that x
2
= y; plugging this into the second,
we get that x
4
+ x = 0 = x(x
3
+ 1), so x = 0 or 1 . Plugging this back into the rst equation gives
y = 0 or 1, so (0, 0) and (1, 1) are the only two critical point.
3. Find all critical points of f(x, y) = xy
2
x
2
2y
2
and determine whether each is a local minimum,
local maximum, or saddle point.
Solution. We want f =

0, and we can calculate f = y
2
2x, 2xy 4y. So, we want y
2
2x = 0
and 2xy 4y = 0. The rst equation tells us that x =
y
2
2
; plugging this into the second equation gives
y
3
4y = 0. We can factor this as y(y 2)(y + 2) = 0, so y = 0, 2, or 2. Since x =
y
2
2
, this gives us
three points, (0, 0) and (2, 2).
To classify our three critical points, we need to calculate the discriminant f
xx
f
yy
f
2
xy
at each point.
Lets rst just calculate it in terms of x and y: f
xx
= 2, f
xy
= 2y, and f
yy
= 2x4, so f
xx
f
yy
f
2
xy
=
4(x 2) 4y
2
. So:
At (0, 0), the discriminant is 8, which tells us that (0, 0) is either a local minimum or a lo-
cal maximum. To decide which, we can use the fact that f
xx
= 2 < 0, which tells us that
(0, 0) is a local maximum .
At (2, 2), the discriminant is 16, so (2, 2) is a saddle point .
At (2, 2), the discriminant is 16, so (2, 2) is a saddle point .
4. Find the points on the cone z
2
= x
2
+ y
2
that are closest to the point (4, 2, 0).
Solution. The distance from a point (x, y, z) to (4, 2, 0) is

(x 4)
2
+ (y 2)
2
+ z
2
. Finding minimal
values of distance is the same as nding minimal values of the square of the distance. So we let
f = (x 4)
2
+ (y 2)
2
+ z
2
and search for the minimum of f.
Before nding the critical points, notice that if (x, y, z) is on the cone, z is dependent on x, y, so we
substitute z
2
= x
2
+ y
2
in f then f = f(x, y) = (x 4)
2
+ (y 2)
2
+ x
2
+ y
2
is a function of two free
variables. Next, f
x
= 2(x 4) + 2x = 4x 8, f
y
= 2(y 2) + 2y = 4y 4. Therefore f
x
= f
y
= 0
implies x = 2, y = 1. D = f
xx
f
yy
f
2
xy
= 4 4 0
2
= 16. The point x = 2, y = 1 is a minimum.
z
2
= 2
2
+ 1
2
= 5, z =

5 or

5.
Conclusion: (2, 1,

5) and (2, 1,

5) are the closest point to (4, 2, 0) on the cone.

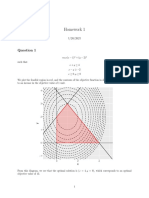
5. Find the absolute maximum and minimum values of f(x, y) = y
2
x
2
on the square |x| 1, |y| 1.
Solution. Since |x| 1, |y| 1 is a closed bounded region in R
2
, we know that f(x, y) must attain
its maximum and minimum values on this region. Remember that the basic strategy is to check the
1
critical points and boundary separately. That is, well nd all the critical points, and then well nd all
the points on the boundary where the absolute minimum or maximum might occur; after weve done
that, well plug each point into f to see which gives the highest value and which gives the lowest.
The critical points are where =

0. Since f = 2x, 2y, the only critical point is (0, 0).
(1)
Now, we look at the boundary. The boundary is composed of four separate pieces, and well look at
each one individually:
Lets look at the piece where x = 1. Here, f(x, y) = f(1, y) = y
2
1, and we are concerned with
y in the interval [1, 1]. So, we want to maximize and minimize y
2
1 on the interval [1, 1].
You can do this using calculus or just by looking at the graph of y
2
1; either way, you should
nd that its biggest when y = 1 and smallest when y = 0. This gives us three candidate points,
(1, 1), (1, 1), and (1, 0).
On the piece where x = 1, f(x, y) = f(1, y) = y
2
1, and we again want to maximize and
minimize y
2
1 on the interval [1, 1]. The maximum is when y = 1 and the minimum is when
y = 0. This gives us three more candidate points, (1, 1), (1, 1), and (1, 0).
On the piece y = 1, f(x, y) = f(x, 1) = 1 x
2
, and we want to maximize and minimize this on
the interval [1, 1]. The maximum occurs when x = 0, and the minimum occurs when x = 1,
so we get three more candidates, (0, 1), (1, 1), and (1, 1).
On the piece y = 1, f(x, y) = f(x, 1) = 1 x
2
, and we get three more candidates, (0, 1),
(1, 1), and (1, 1).
So, we now have a big list of points where the absolute minimum and maximum might occur: (0, 0),
(1, 1), (1, 1), (1, 0), (1, 1), (1, 1), (1, 0), (0, 1), (1, 1), (1, 1), (0, 1), (1, 1), and (1, 1).
We evaluate f at each of these points, and we nd that the absolute maximum occurs at (0, 1), where
the function is equal to 1. The absolute minimum occurs at (1, 0), where the function is equal to
1.
6. Find the absolute maximum and minimum values of 2x
3
+y
4
on the unit disk D = {(x, y) | x
2
+y
2
1}.
Solution. Let f(x, y) = 2x
3
+ y
4
, Since D is a closed and bounded region and f is continuous, we
know f must have attain global maximum and minimum in D.
Step 1: Find critical points: f
x
= 6x
2
, f
y
= 4y
3
, and hence the only critical point is (0, 0) and its
indeed in D. f(0, 0) = 0.
Step 2: On the boundary x
2
+ y
2
= 1,
f(x, y) = 2x
3
+ y
4
= 2x
3
+ (1 x
2
)
2
= x
4
+ 2x
3
2x
2
+ 1.
Thus we regard it as a function of only one variable x and nd extremum. This can be done by taking
derivative f

= 4x
3
+ 6x
2
= 4x and set it equal to zero. f

= 2x(2x 1)(x + 2) therefore x = 0 or 1/2

(x = 2 is not in D). The correspoding points and values are f(0, 1) = 1, f(
1
2
,

3
2
) =
13
16
. Dont
forget about the endpoint x = 1 and x = 1, they are f(1, 0) = 2, f(1, 0) = 2.
Step 3: After comparing all candidates, we nd f(1, 0) = 2 is the global minimum and f(1, 0) = 2
is the global maximum.
(1)
You can use the Second Derivative Test to see what type of critical point (0, 0) is, but its not necessary to do so since we
are really just compiling a list of candidate points that we will check later.
2