University of Portsmouth, Department of Electronic and Computer Engineering

B307 Discrete and Modern Control Systems Design - Lecture 3/Tutorial 1

Branislav Vuksanovic

Tutorial 1 - State Space Equations

1. Prove that the state space model of the R-L-C circuit system analysed in the previous
lecture can be expressed in the form:
State equation: ( ) ( ) ( )
0 1 0
1 1
t t t
R
LC L LC


= +



x x u
i

Output equation: ( ) [ ] ( ) 1 0 t t = y x
if state variables are defined as ( ) ( )
1 0
x t v t = and ( ) ( ) 0
2
x t v t =
i
.

2. Classify each of the following state-space models as being linear/nonlinear and time-
varying/time-invariant. For each LTI (linear-time-invariant) system, determine its order,
evaluate the corresponding transfer function and write down the poles of the system.
a)
( )
1 2
2 1 1 2
1
2 1
x x
x x x x u
y x
=
= + +
=
i
i

b)
1 2
2 1 2
1
2
x x
x x x u
y x
=
= +
=
i
i

c)
( )
1 2
2 1 2
1
sin
2
x t x
x x x u
y x
=
= +
=
i
i

d)
1 1 3 1
2 2 3 2
3 1
1 1 3
2 2 3
5
3
6
x x x u
x x x u
x x
y x x
y x x
= +
= + +
=
= +
= +
i
i
i


3. Derive a state-space model for each of the following systems. Define as state
variables
1
x y = ,
2
x y =
i
and for b)
3
x y =
ii
.
a) The mass-spring-damper system described by the second-order differential
equation:
( ) ( ) ( ) ( ) m y t b y t ky t u t + + =
ii i

b) A third order system with input u(t) and output y(t) related by:
( ) ( ) ( )
( ) ( )
3 2
2 1 0 3 2
d y t d y t dy t
a a a y t bu t
dt dt dt
+ + + =
University of Portsmouth, Department of Electronic and Computer Engineering
B307 Discrete and Modern Control Systems Design - Lecture 3/Tutorial 1

Branislav Vuksanovic


4. Derive a state-space model for a general SISO system. You can use an n-th order
differential equation to describe this system:
( ) ( ) ( )
( ) ( )
1
1 1 0 1
...
n n
n n n
d y t d y t dy t
a a a y t u t
dt dt dt

+ + + + =

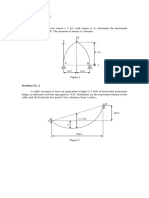
5. Figure 1 shows a field-controlled dc servomotor which produces a torque T Ki = . Let J =
moment of inertia of all moving parts referred to the motor shaft, and b =coefficient of
viscous damping. Determine a state-space model which relates the output angular
position of the load to the input voltage v. Define as state variables
1
x = ,
2
x =
i
and
3
x =
ii
.

Figure 1.

6. Complex machine system is modelled as two masses connected by a flexible structure.
One mass carries all the drive and the other all the instruments. The drive mass is isolated
from instrumentation structure by a spring and damper. Find the state space model for the
system, shown in Figure 2 below using the velocity and displacement of the two masses
as the state variables. Regard the displacement of the second mass as the system output.

Figure 2.

University of Portsmouth, Department of Electronic and Computer Engineering
B307 Discrete and Modern Control Systems Design - Lecture 3/Tutorial 1

Branislav Vuksanovic

SOLUTIONS:

1. Start from the second order differential equation derived in lecture:
( ) ( ) ( ) ( )
1 1
o o o
R
v t v t v t u t
L LC LC
+ + =
ii i

and define two state variables:
( ) ( )
( ) ( )
1
2
o
o
x t v t
x t v t
=
=
i

to obtain specified state space model.

2.
a)
( )
1 2
2 1 1 2
1
2 1
x x
x x x x u
y x
=
= + +
=
i
i

System is time invariant, but non-linear
b)
1 2
2 1 2
1
2
x x
x x x u
y x
=
= +
=
i
i

This is an LTI system
c)
( )
1 2
2 1 2
1
sin
2
x t x
x x x u
y x
=
= +
=
i
i


System is linear but time-varying
d)
1 1 3 1
2 2 3 2
3 1
1 1 3
2 2 3
5
3
6
x x x u
x x x u
x x
y x x
y x x
= +
= + +
=
= +
= +
i
i
i

This is an LTI system

For LTI system b): ( )
( )( )
1
1 2
TF G s
s s
= =
+ +

For LTI system d): ( )
( )
( )( )
( )
( )( )( )
6
0
2 3
6 2
1
1 2 3 1
s
s s
TF G s
s
s s s s
+

+ +

= =

+ + + +



University of Portsmouth, Department of Electronic and Computer Engineering
B307 Discrete and Modern Control Systems Design - Lecture 3/Tutorial 1

Branislav Vuksanovic


3.
a)
0 1
A
k b
m m


=



,
0
1
B
m


=


,
[ ] 1 0 C = , 0 D =
b)
0 1 2
0 1 0
0 0 1 A
a a a


=



,
0
0 B
b


=



,
[ ]
1 1 0 C = , 0 D =

4. Start from derived n
th
order differential equation:
( ) ( ) ( )
( ) ( )
1
1 1 0 1
...
n n
n n n
d x t d x t dx t
a a a x t f t
dt dt dt

+ + + + =
and define n-1 state variables:
( ) ( )
( )
( )
( )
( )
1
2
1
1
.
.
.
n
n n
x t q t
dq t
x t
dt
d q t
x t
dt

=
=
=

to obtain:
0 1 2
0 1 0 ... 0
0 0 1 0
...
0 0 0 1
n
A
a a a a



=





,
0
0
...
0
1
B



=





(after some mathematical manipulations)
NOTE: No output equation was considered, so matrices C and D are not derived.

5.
0 1 0
0 0 1
0
A
Rb b R
JL J L



=



+



,
0
0 B
K
JL



=




,
[ ]
1 0 0 C = , 0 D =
University of Portsmouth, Department of Electronic and Computer Engineering
B307 Discrete and Modern Control Systems Design - Lecture 3/Tutorial 1

Branislav Vuksanovic

6.
1 1 1 1
2 2 2 2
0 1 0 0
0 0 0 1
k b k b
m m m m
A
k b k b
m m m m





=






,
1
0
1
0
0
m B



=




,
[ ] 0 0 1 0 C = , 0 D =