14

: APPENDIX

Polynomials and
Difference Equations

A time-series model is one which postulates a relationship amongst a number of temporal sequences or time series. For example, we have the regression
model
(1)

y(t) = x(t) + (t)

where x(t) is an observable sequence indexed by the time subscript t and (t) is
an unobservable sequence of independently and identically distributed random
variables.
A more general model, which we shall call the general temporal regression model, is one which postulates a relationship comprising any number of
consecutive elements of x(t), y(t) and (t). Thus we have
(2)

p
X

i y(t i) =

i=0

k
X

i x(t i) +

i=0

q
X

i (t i)

i=0

Any of the sums in this expression can be infinite, but if the model is to be
viable, the sequences of coefficients {i }, {i } and {i } can depend on only a
limited number of parameters.
We are particularly interested in a number of specialisations of the model.
The model represented by the equation
(3)

y(t) = x(t i) +

q
X

i (t i)

i=0

is described asP
a regression model with a serially correlated disturbance sequence (t) =
i (t i). If this sum is finite, then (t) is called a moving
average process. The model represented by
(4)

p
X

i y(t i) = x(t) + (t)

i=0

D.S.G. POLLOCK : ECONOMETRIC THEORY

is described as an autoregressive regression model. The equation
(5)

y(t) =

i x(t i) + (t)

i=0

represents the distributed-lag regression model.

The foregoing models are all termed regression models by virtue of the
inclusion of the observable explanatory sequence x(t). When x(t) is deleted, we
obtain the simpler unconditional linear stochastic models. Thus the equation
(6)

y(t) =

q
X

i (t i),

i=0

where the sum is finite, represents a moving average process; whereas

p
X

(7)

i y(t i) = (t),

i=0

again with a finite sum, represents an autoregressive process. The equation

(8)

p
X

i y(t i) =

i=0

q
X

i (t i)

i=0

represents an autoregressive-moving average process.

The Algebra of the Lag Operator
A sequence x(t) is any function mapping from the set of integers Z =
{0, 1, 2, . . .} to the real line. If the set of integers represents a set of dates
separated by unit intervals, then we say that x(t) is a temporal sequence or
time series.
The set of all time series represents a vector space, and we can define
various linear transformations or operators over the space. For example, we
define the lag operator by
(9)

Lx(t) = x(t 1).

Now, L{Lx(t)} = Lx(t 1) = x(t 2); so it makes sense to define L2 by

L2 x(t) = x(t 2). More generally, Lk x(t) = x(t k) and, likewise, Lk x(t) =
x(t + k). Other operators are the difference operator = I L which has the
effect that
(10)

x(t) = x(t) x(t 1),

2

D.S.G. POLLOCK : POLYNOMIALS

the forward-difference operator = L1 I, and the summation operator
S = (I L)1 = {I + L + L2 + } which has the effect that
(11)

Sx(t) =

x(t i).

i=0

In general, we can define polynomials

of the lag operator of the form p(L) =
P
pi Li having the effect that
p0 + p1 L + p2 L2 + + pn Ln =

(12)

p(L)x(t) = p0 x(t) + p1 x(t 1) + + pn x(t n)

n
X
=
pi x(t i).
i=0

The advantage which comes from defining polynomials in the lag operator
stems from the fact that they are isomorphic to the set of ordinary algebraic
polynomials. Thus we can rely upon what we know about ordinary polynomials
to treat problems concerning lag-operator polynomials.
Algebraic Polynomials
Consider the equation 0 + 1 z + 2 z 2 = 0. On dividing the equation by
2 , we can factorise it as (z 1 )(z 2 ) where 1 , 2 are the roots of the
equation that are given by the formula
(13)

p
12 42 0
.
22

If 12 42 0 , then the roots 1 , 2 are real. If 12 = 42 0 , then 1 = 2 .

If 12 42 0 , then theroots are the conjugate complex numbers = + i,
= i where i = 1.
Complex Roots
There are three alternative ways of representing the conjugate complex
numbers and :
(14)

= + i = (cos + i sin ) = ei ,
= i = (cos i sin ) = ei ,

where
(15)

(2 + 2 )

and
3

= tan1

D.S.G. POLLOCK : ECONOMETRIC THEORY

These are called, respectively, the Cartesian form, the trigonometrical form and
the exponential form.
The polar representation is understood by considering the Argand diagram:

Im

Re

Figure 1. The Argand Diagram showing a complex

number = + i and its conjugate = i .

The exponential form is understood by considering the following series

expansions of cos and i sin about the point = 0:
4
6
2
+

+
2!
4!
6!
i3
i5
i7
i sin = i
+

+
3!
5!
7!
cos = 1

(16)

Adding these gives us Eulers equation:

(17)

cos + i sin = 1 + i

i3
4
2

+
+
2!
3!
4!

= ei .
Likewise, by subtraction, we get
(18)

cos i sin = ei .

It follows readily from (17) and (18) that

(19)

cos =

ei + ei
2
4

D.S.G. POLLOCK : POLYNOMIALS

and
i(ei ei )
2
ei ei
=
.
2i

sin =
(20)

The n-th Order Polynomial

Now consider the general equation of the nth order:
0 + 1 z + 2 z 2 + + n z n = 0.

(21)

On dividing by n , we can factorise this as

(z 1 )(z 2 ) (z n ) = 0,

(22)

where some of the roots may be real and others may be complex. The complex
roots come in conjugate pairs, so that, if = + i is a complex root, then
there is a corresponding root = i such that the product (z)(z ) =
z 2 + 2z + (2 + 2 ) is real and quadratic. When we multiply the n factors
together, we obtain the expansion
X
XX
i z n1 +
i j z n2 (1)n 1 2 n .
(23)
0 = zn
i

We can compare this with the expression (0 /n )+(1 /n )z + +z n = 0.QBy

equating coefficients of the two expressions, we find that (0 /n ) = (1)n i
or, equivalently,
(24)

n = 0

n
Y

(i )1 .

i=1

Thus we can express the polynomial in any of the following forms:

X
Y
i z i = n (z i )
Y
Y
= 0 (i )1 (z i )
(25)

Y
z
.
1
= 0
i
P
We should also note that, if is a P
root of the equation
i z i = 0,
then = 1/ is a root of the equation
i z ni = 0. This follows since
5

D.S.G. POLLOCK : ECONOMETRIC THEORY

P
P
P
i i =
i i = 0. Confusion
i ni = n i i = 0 implies that
can arise from not knowing which of the two equations one is dealing with.
P

Rational Functions of Polynomials

If (z) and (z) are polynomial functions of x of degrees n and m respectively with n < m, then the ratio (z)/(z) is described as a proper rational
polynomial. We shall often encounter expressions of the form
y(t) =

(L)
x(t).
(L)

For this to have a meaningful interpretation in the context of a time-series

model, we normally require that y(t) should be a bounded sequence whenever
x(t) is bounded. The necessary and sufficient condition for the boundedness of
y(t), in that case, is that the series expansion of (z)/(z) should be convergent
whenever |z| 1. We can determine whether or not the sequence will converge
by expressing the ratio (z)/(z) as a sum of partial fractions. The basic result
is as follows:
(26)

If (z)/(z) = (z)/{1 (z)2 (z)} is a proper rational fraction, and

if 1 (z) and 2 (z) have no common factor, then the fraction can
be uniquely expressed as
1 (z)
2 (z)
(z)
=
+
,
(z)
1 (z) 2 (z)
where 1 (z)/1 (z) and 2 (z)/2 (z) are proper rational fractions.

Q
Imagine that (z) = (1 z/i ). Then repeated applications of this basic
result enables us to write
2
n
1
+
+ +
.
(27)
(z) =
1 z/1
1 z/2
1 z/n
By adding the terms on the RHS, we find an expression with a numerator of
order n 1. By equating the terms of the numerator with the terms of (z),
we can find the values 1 , 2 , . . . , n .
Consider, for example,

(28)

3x
3x
=
1 + x 2x2
(1 x)(1 + 2x)
2
2
=
+
1 x 1 + 2x
1 (1 + 2x) + 2 (1 x)
.
=
(1 x)(1 + 2x)
6

D.S.G. POLLOCK : POLYNOMIALS

Equating the terms of the numerator gives
(29)

3x = (21 2 )x + (1 + 2 ),

so that 2 = 1 which gives 3 = (21 2 ) = 31 ; and thus we have 1 = 1,

2 = 1.
The conditions for the convergence of the expansion of (z)/(z) are
straightforward. For the rational function converges if and only if the expansion
of each of its partial fractions converges. For the expansion
n
o

(30)
= 1 + z/ + (z/)2 +
(1 z/)
to converge when |z| 1, it is necessary and sufficient that || > 1.
Linear Difference Equations
An nth-order linear difference equation is a relationship amongst n + 1
consecutive elements of a sequence x(t) of the form
(31)

0 x(t) + 1 x(t) + + n x(t n) = u(t),

where u(t) is some specified sequence. We can also write this as

(32)

(L)x(t) = u(t),

where (L) = 0 + 1 L + 2 L2 + + n Ln . If we are given n consecutive

values of x(t), say x1 , x2 , . . . , xn , then we can use this relationship to find the
succeeding value xn+1 . In this way, so long as u(t) is fully specified, we can
generate all the succeeding elements of the sequence. Likewise, we can generate
all the values of the sequence prior to t = 1; and thus, in effect, we can deduce
the function x(t) from the difference equation. However, instead of a recursive
solution, we usually seek an analytic expression for x(t).
The function x(t; c), expressing the analytic solution, will comprise a set
of n constants in c = [c1 , c2 , . . . , cn ]0 which can only be determined once we are
given a set of n consecutive values of x(t) which are called initial conditions.
The general analytic solution of the equation (L)x(t) = u(t) is expressed as
x(t; c) = y(t; c) + z(t), where y(t) is the general solution of the homogeneous
equation (L)y(t) = 0, and z(t) = 1 (L)u(t) is called a particular solution of
the inhomogeneous equation.
We solve the difference equation in three steps. First, we find the general
solution of the homogeneous equation. Next, we find the particular solution
z(t) which embodies no unknown quantities. Finally, we use the n initial values
of x to determine the constants c1 , c2 , . . . , cn . We shall discuss in detail only
the solution of the homogeneous equation.
7

D.S.G. POLLOCK : ECONOMETRIC THEORY

Solution of the Homogeneous Difference Equation
If j is a root of the equation (z) = 0 + 1 z + 2 z 2 + + n z n = 0 such
that (j ) = 0, then yj (t) = (1/j )t is a solution of the equation (L)y(t) = 0.
We can see this by considering the expression

(L)

1
j

t
= (0 + 1 L + + n Ln )

= 0

(33)

1
j

+ 1

1
j

t1

= (j )

1
j

+ + n

= (0 + 1 j + + n nj )

1
j

1
j

1
j

tn

Q
Alternatively, consider the factorisation (L) = 0 i (1 L/j ). Within this
product, we have the term 1 L/j and, clearly, since

L
1
j

1
j

t
=

1
j

1
j

t
= 0,

we must have (L)(1j )t = 0.

The general solution, in the case where (L) = 0 has distinct real roots, is
given by

(34)

y(t; c) = c1

1
1

+ c2

1
2

+ + cn

1
n

t
,

where c1 , c2 , . . . , cn are the constants which are determined by the initial conditions.
In the case where two roots coincide at a value of , the equation (L)y(t)
= 0 has the solutions y1 (t) = (1/)t and y2 (t) = t(1/)t . To show
this, let
Q
us extract the term (1 L/)2 from the factorisation (L) = 0 i (1 L/j )
given under (25). Then, according to the previous argument, we have (1
L/)2 (1/)t = 0, but, also, we have

(35)

L
1

2 t
t
2L L2
1
1
+ 2 t
t
= 1

t
t
1
1
1
=t
+ (t 2)
= 0.
t 2(t 1)

D.S.G. POLLOCK : POLYNOMIALS

In general, if there are r repeated roots, then (1/)t , t(1/)t , t2 (1/)t , . . . ,
tr1 (1/)t are all solutions to the equation (L)y(t) = 0.
The 2nd-order Difference equation with Complex Roots
Imagine that the 2nd-order equation (L)y(t) = 0 y(t) + 1 y(t 1) +
2 y(t 2) = 0 is such that (z) = 0 has complex roots = 1/ and = 1/ .
Let us write
(36)

= + i = (cos + i sin ) = ei ,
= i = (cos i sin ) = ei .

These will appear in a general solution of the difference equation of the form of
(37)

y(t) = ct + c ( )t .

This is a real-valued sequence; and, since a real term must equal its own conjugate, we require c and c to be conjugate numbers of the form
(38)

c = (cos + i sin ) = ei ,
c = (cos i sin ) = ei .

Thus we have

(39)

ct + c ( )t = ei (ei )t + ei (ei )t
n
o
= t ei(t) + ei(t)
= 2t cos(t ).

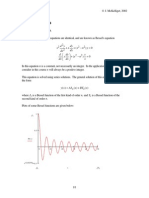
To analyse the final expression, consider first the factor cos(t ). This
is a displaced cosine wave. The value , which is a number of radians per unit
period, is called the angular velocity or the angular frequency of the wave. The
value f = /2 is its frequency in cycles per unit period. The duration of one
cycle, also called the period, is r = 2/.
The term is called the phase displacement of the cosine wave, and it
serves to shift the cosine function along the axis of t so that the peak occurs at
the value of t = / instead of at t = 0.

Next consider the term t wherein = ( 2 + 2 ) is the modulus of the

complex roots. When has a value of less than unity, it becomes a damping
factor which serves to attenuate the cosine wave as t increases.
Finally, the factor 2 represents the initial amplitude of the cosine wave
which is the value that it assumes when t = 0. Since is just the modulus of
the values c and c , this amplitude reflects the initial conditions.
9