Professional Documents
Culture Documents
Chapter 3 - Integration
Uploaded by
Muhamad NazrinOriginal Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Chapter 3 - Integration
Uploaded by
Muhamad NazrinCopyright:
Available Formats
SFM 1002 Mathematics II
Chapter 3 Integration
CHAPTER 3
INTEGRATION
________________________________________________________________________
At the end of chapter, the students are able to
find the anti-derivative of a function (C1)
trace the anti-derivative rule to find the integration of the polynomial, trigonometric,
exponential, and logarithmic function (P3, C1)
trace and use the integration by substitute and integration by part to find the antiderivative of the function (P3, C3)
find the definite integration (C1)
trace the concept of definite integration to find the area under the line (P3, C1)
sketch the graph and find the area of the region between 2 lines (C3)
________________________________________________________________________
3.1
Indefinite Integration
Definition 3.1: An anti-derivative of a function g (x) is any function f (x) such that
g ( x)= f '( x) for each x in the domain of g (x) .
Definition 3.2: The set of all anti-derivative of g (x) is the indefinite integral of g (x) with
respect to x , denoted by
g ( x)dx =
f ( x) + C .
Example 3.1(a): Find the derivative of the function f ( x) = x 2 + x + 1 . If g ( x) = f ' ( x) , find
anti-derivative of g (x) .
Solution:
f ' ( x) = 2 x + 1 ;
Therefore, g ( x) = 2 x + 1 .
2 x + 1dx = x
+ x+C .
Example 3.1(b): Find the derivative of the function f ( x) = 2 x 3 + 3 x + 4 . If g ( x) = f ' ( x) , find
anti-derivative of g (x) .
29
SFM 1002 Mathematics II
Chapter 3 Integration
Proposition 3.1(Rules of Anti-derivative): The indefinite Integral function of g (x) can be
found by integral formula as follow:
a) 0dx = C
b)
kdx = kx + C
x n +1
+ C , for n 1
n +1
1
d) x 1 dx = dx = ln x + C
x
x
x
e) e dx = e + C
c)
f)
g)
h)
i)
j)
k)
l)
m)
n
x dx =
e f ' ( x)dx = e + C
sin xdx = cos x + C
cos xdx = sin x + C
tan xdx = ln sec x + C
cot xdx = ln sin x + C
sec xdx = tan x + C
csc xdx = cot x + C
sec x tan xdx = sec x + C
f ( x)
f ( x)
n) [ f ( x) g ( x)] dx = f ( x)dx g ( x)dx
o) k f ( x)dx=k f ( x)dx
Example 3.2: Solve the following problems.
a) 7 dx
Solution:
b)
x dx
5
Solution:
c)
x dx = 6 x
5
+C
+ sin xdx
Solution:
d)
7dx = 7 x + C
5 x
+ sin xdx =
1 3
x cos x + C
3
dx
Solution:
5 x
dx =
1
1
e 5 x (5)dx = e 5 x + C
5
5
30
SFM 1002 Mathematics II
Chapter 3 Integration
e)
cot x + 2e
2 x e x + x 4 3 x 2 + 7 dx
2
Proposition 3.2: If f (x) is a differentiable function, g (x) is a continuous function, and G (x)
is an anti-derivative of g (x) , then
g ( f ( x)) f ' ( x)dx = G( f ( x)) + C .
Besides that, the integration can be done by another way.
du = f ' ( x)dx , then
Suppose that u = f (x) and
g ( f ( x)) f ' ( x)dx = g (u ) du = G(u ) + C = G( f ( x)) + C .
This method is
called integration by substitution.
Substitution Method:
To integrate the function
Step 1:
Step 2:
Choose u = f (x) and du = f ' ( x)dx ,
Substitute u and du into the equation, then we got
g ( f ( x)) f ' ( x)dx = g (u ) du
Integrate
Step 3:
g ( f ( x)) f ' ( x)dx , we need to the follow:
g (u ) du = G(u ) + C
Replace u = f (x) into G (u ) + C
Example 3.3: Solve the following problems.
a) ( x + 3) 7 dx
Solution:
Step 1:
Step 2:
Step 3:
Let u = x + 3 , then du = dx
1 8
7
7
( x + 3) dx = u du = 8 u + C
Replace u = x + 3 , therefore
( x + 3)
1
dx = ( x + 3)8 + C
8
31
SFM 1002 Mathematics II
Chapter 3 Integration
b)
3x
( x 3 + 1) 5 dx
Solution:
Step 1:
Step 2:
Step 3:
c)
Let u = x 3 + 1 , then du = 3 x 2 dx
1 6
u +C
6
1
Replace u = x 3 + 1 , therefore 3 x 2 ( x 3 + 1) 5 dx = ( x 3 + 1) 6 + C
6
3x
( x 3 + 1) 5 dx = ( x 3 + 1) 5 3 x 2 dx = u 5 du =
(2e x + 3)10 dx
Proposition 3.3: The formula for integration by parts is udv = uv vdu .
When integration by substitution does not work, we can use integration by parts to solve the
problem.
Example 3.4: Solve the following problems.
a) x cos xdx
Solution:
Step 1:
Step 2:
Step 3:
Choose u = x , then du = dx
Choose dv = cos xdx , then v = sin x
x cos xdx = x sin x sin xdx = x sin x ( cos x) + C
= x sin x + cos x + C
32
SFM 1002 Mathematics II
Chapter 3 Integration
b)
xe
dx
Solution:
Step 1:
Step 2:
Step 3:
c)
Choose u = x , then du = dx
Choose dv = e x dx , then v = e x
x
x
x
x
x
xe dx = xe e dx = xe e + C
sin xdx
Solution:
Step 1:
Step 2:
Step 3:
Choose u = e x , then du = e x dx
Choose dv = sin xdx , then v = cos x
x
x
x
x
x
e sin xdx = e ( cos x) cos x e dx = e cos x + cos x e dx
Step 1a:
Step 2a:
Choose u1 = e x , then du1 = e x dx
Choose dv1 = cos xdx , then v1 = sin x
Step 3a:
cos xdx = e x sin x sin x e x dx
Replace e x cos xdx = e x sin x sin x e x dx into e x sin xdx , then
sin xdx = e x cos x + (e x sin x sin x e x dx)
= e x cos x + e x sin x sin x e x dx
2 e x sin xdx = e x cos x + e x sin x
e x sin xdx =
d)
1
1
(e x cos x + e x sin x) = e x (sin x cos x)
2
2
x ln xdx
33
SFM 1002 Mathematics II
Chapter 3 Integration
3.2
Define Integration and Its Applications
Proposition 3.4: If f (x) is continuous at every point in [a, b] and F (x) is any anti-derivative
b
of f (x) on [a, b] , then
f ( x)dx = F (b) F (a) .
a
Method:
b
To integrate the function
f ( x)dx = F (b) F (a) , we need to the follow:
a
f ( x)dx , and let
Step 1:
Find
Step 2:
Find F (a ) and F (b) .
F ( x) = f ( x)dx .
b
Step 3:
Replace into the equation
f ( x)dx = F (b) F (a) .
a
Example 3.5: Solve the following problems.
2
a)
3x
dx
Solution:
Step 1: 3 x 2 dx = x 3 + C = F ( x)
Step 2: F (2) = 8 + C and F (1) = 1 + C
2
Step 3:
3x dx = F (2) F (1) = 7
2
b)
sin x + 2 xdx
0
34
SFM 1002 Mathematics II
Chapter 3 Integration
Proposition 3.5 (Properties of Definite Integrals): If f (x) and g (x) are integrable, then the
definite integral satisfied the following rules.
a)
f ( x)dx = f ( x)dx
a
b)
f ( x)dx =0
a
c)
k f ( x)dx = k f ( x)dx , for any number k
b
d)
e)
f ( x) g ( x)dx = f ( x)dx g ( x)dx
a
f ( x)dx + f ( x)dx = f ( x)dx
Proposition 3.6: The area under the line y = f (x) over the interval [a, b] can be found by using
b
A = f ( x)dx .
a
y = f (x)
x
a
Figure 3.1: Area Under the Line y = f (x) Over the Interval [a, b]
Example 3.6: Find the area under the line y = 3x 2 over the interval [1,2] .
Solution:
b
A = f ( x)dx = 3x 2 dx = x 3 = 8 1 = 7 unit 2
2
Note: We can use the method which is shown at Example 3.5 to find the answer.
35
SFM 1002 Mathematics II
Chapter 3 Integration
Proposition 3.7: If f (x) and g (x) are continuous over the interval [a, b] , then the area of the
b
region between the lines y1 = f ( x) and y 2 = g ( x) is A = f ( x) g ( x)dx , where y1 = f ( x) is
a
upper line and y 2 = g ( x) is lower line.
y
y 2 = g ( x)
y1 = f ( x)
x
a
Figure 3.2: The Area of The Region Between The Lines y1 = f ( x) And y 2 = g ( x) over the
interval [a, b]
Method:
To find the area of the region between 2 lines y1 and y2 over the interval [a, b] ,
we need to the follow:
Step 1:
Sketch the graph.
Step 2:
Determine the upper line and lower line.
b
Step 3:
Compute A = f ( x) g ( x)dx , where f (x) is upper line and
a
g (x) is lower line.
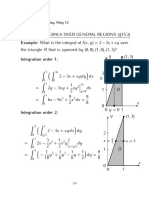
Example 3.7(a): Find the area of the region between the lines y1 = 2 x and y2 = x 2 3 over the
interval [1,2] .
Solution:
Step 1:
Sketch the graph
36
SFM 1002 Mathematics II
Chapter 3 Integration
y2 = x 2 3
y1 = 2 x
Step 2:
Upper line: y1 = 2 x
Lower line: y2 = x 2 3
Step 3:
A = f ( x) g ( x)dx = (2 x) ( x 2 3)dx = x 2 + 2 x + 3dx
1
2
1
1
1
= ( x 3 + x 2 + 3 x) = (2) 3 + (2) 2 + 3(2) (1) 3 + (1) 2 + 3(1)
3
3
3
1
22 11 11
= = unit 2
3 3 3
Example 3.7(b): Find the area of the region between the lines y1 = x 2 and y2 = x 2 + 2 over the
interval [1,1] .
37
SFM 1002 Mathematics II
Chapter 3 Integration
Exercise 3:
In Problem 1-22, evaluate the indefinite integrals.
1. 5dx
12. x 2 ( x 3 + 5 x 2 x + 3 )dx
3
2
3 )dx
2
x
x
2x 3
14. (
+ 5 )dx
x
x
6
4
4 x + 3x
15.
dx
x3
x6 x
16.
dx
x3
13. (
2. ( x 4)dx
3. ( x 2 )dx
4. (3 x 2 3 )dx
5
5. x 4 dx
2
3
6. 3 x dx
7.
17. ( x 3 + x)dx
18. ( x 3 + x )dx
dx
8. 7 x 4 dx
19. ( x + 1) 2 dx
9. ( x 2 x)dx
( z + 2 z ) dz
21. (3 sin 4 cos )d
22. (3 cos 4 sin +
2
20.
10. (3 x 2 x)dx
11. (4 x 5 x 3 )dx
) d
In Problem 1-14, use the First Fundamental Theorem of Calculus to evaluate each definite
integral.
1.
2.
3.
4.
x 3 dx
8.
x 4 dx
9.
(3 x 2 2 x + 3)dx
(4 x + 7)dx
3
1
dw
1 w2
3 2
6. 3 dt
1 t
5.
7.
t dt
10.
12.
14.
wdw
11.
13.
(y 2 +
s4 8
ds
s2
2
0
cos xdx
2 sin tdt
(2 x
0
1
)dy
y3
3 x 2 + 5)dx
1
( x 3 2 x 3 )dx
38
SFM 1002 Mathematics II
Chapter 3 Integration
Use the method of substitution to find each of the following indicated integrals.
1. (2 x + 3) 4 dx
6. x(3 x 2 5) 50 dx
7.
3. (11 2 x) dx
8.
4. ( x 2 cos 3 x)dx
9.
2
x( x + 3)
2.
3t 5dt
4
5
5.
x(3x
5)dx
2 x 3 5dx
( x 3 + 5) 9 dx
12
7
dx
1
8
10. (6 x 7) dx
Find the areas of the regions enclosed by the lines and curves in the following questions.
1.
y = x 2 2 and y = 2 over the interval [2,2]
2.
y = 2 x x 2 and y = 3 over the interval [1,3]
3.
y = x 4 and y = 8 x over the interval [0,2]
4.
y = x 2 2 x and y = x over the interval [0,3]
5.
y = x 2 and y = x 2 + 4 x over the interval [0,2]
6.
y = 7 2 x 2 and y = x 2 + 4 over the interval [1,1]
7.
y = x 4 4 x 2 + 4 and y = x 2 over the interval [1,4]
39
You might also like
- Integral CalculusDocument25 pagesIntegral CalculusCarl Kristopher PeloniaNo ratings yet
- Practice Exam3 21b SolDocument6 pagesPractice Exam3 21b SolUmer Iftikhar AhmedNo ratings yet
- Chap 1 Advanced DifferentiationDocument25 pagesChap 1 Advanced Differentiationprakash silvarajanNo ratings yet
- F (X) DX F (X) +C Symbol of IntegrationDocument13 pagesF (X) DX F (X) +C Symbol of IntegrationSyed Mohammad AskariNo ratings yet
- Calculus Cheat Sheet Integrals ReducedDocument3 pagesCalculus Cheat Sheet Integrals ReducedShahnaz GazalNo ratings yet
- Mit Calculus Integral NotesDocument64 pagesMit Calculus Integral Notesalex_58357No ratings yet
- C N X K DX X K DX KX: Integral Calculus - Indefinite IntegralDocument6 pagesC N X K DX X K DX KX: Integral Calculus - Indefinite IntegralCho Yin TangNo ratings yet
- Jan98 MA1002 CalculusDocument6 pagesJan98 MA1002 CalculusZama MakhathiniNo ratings yet
- Lec 26Document6 pagesLec 26raw.junkNo ratings yet
- H2 Mathematics Cheat Sheet by Sean LimDocument27 pagesH2 Mathematics Cheat Sheet by Sean LimGale HawthorneNo ratings yet
- Bab Xiii Integral: 13. 1 DefinisiDocument25 pagesBab Xiii Integral: 13. 1 DefinisiDeazzy AndriyaniNo ratings yet
- Integration PDFDocument8 pagesIntegration PDFAre Peace El MananaNo ratings yet
- 2012 Differentiation Barely PassedDocument10 pages2012 Differentiation Barely PassedcsanjeevanNo ratings yet
- Calculus Cheat Sheet IntegralsDocument5 pagesCalculus Cheat Sheet Integralstasos_rex31390% (2)
- Integration Key FactsDocument7 pagesIntegration Key FactsLauren BuxtonNo ratings yet
- X With Respect To X The Derived Function Is 2x .: IntegrationDocument15 pagesX With Respect To X The Derived Function Is 2x .: IntegrationAdri EnneNo ratings yet
- Fe Tutorials Sem2Document8 pagesFe Tutorials Sem2narendasreNo ratings yet
- Integral Calculus by Arihant B016Document27 pagesIntegral Calculus by Arihant B016Luis Anderson60% (5)
- WAJA 2009: Additional Mathematics Form FiveDocument20 pagesWAJA 2009: Additional Mathematics Form FiveLim Wai Wai SmktpNo ratings yet
- Indefinite IntegrationDocument24 pagesIndefinite IntegrationAditya BansalNo ratings yet
- Theory Definite Integrals PDFDocument35 pagesTheory Definite Integrals PDFvaranasilkoNo ratings yet
- Integration PDFDocument11 pagesIntegration PDFJaymour Cris FiestaNo ratings yet
- Calculus: Differentiation RulesDocument17 pagesCalculus: Differentiation RulesAoSd' TikmanNo ratings yet
- 5 - IntegrationDocument9 pages5 - IntegrationSham JaggernauthNo ratings yet
- DocumentDocument9 pagesDocumentDavid RodriguezNo ratings yet
- F (X) DX F (X) +C Symbol of IntegrationDocument9 pagesF (X) DX F (X) +C Symbol of IntegrationLuCiFeR GamingNo ratings yet
- Maxima and Minima: Basic MathematicsDocument30 pagesMaxima and Minima: Basic MathematicsShrivardhan PatilNo ratings yet
- Homework #2 Solutions Problems: Math 19: Calculus Summer 2010Document6 pagesHomework #2 Solutions Problems: Math 19: Calculus Summer 2010AnaMendezNo ratings yet
- Chain Rule ReverseDocument11 pagesChain Rule ReverseJosué QuintanillaNo ratings yet
- Calculus Cheat Sheet IntegralsDocument5 pagesCalculus Cheat Sheet Integralsapi-322359712No ratings yet
- Unit 1Document62 pagesUnit 1Reetesh DabeedeenNo ratings yet
- Capitolul I INTEGRALE (Recapitulareliceu) : Funcţii Elementare Funcţii Compuse 1) 2) 3) 4) 5)Document49 pagesCapitolul I INTEGRALE (Recapitulareliceu) : Funcţii Elementare Funcţii Compuse 1) 2) 3) 4) 5)EugenhoNo ratings yet
- 10 - Integration WorksheetDocument18 pages10 - Integration WorksheetAs EdNo ratings yet
- Math 105 Practice Exam 3 SolutionsDocument3 pagesMath 105 Practice Exam 3 SolutionsexamkillerNo ratings yet
- Anti-Differentiation (Integration) : y X + y X + yDocument4 pagesAnti-Differentiation (Integration) : y X + y X + ygilalulaNo ratings yet
- Differential Equations: Introduction ToDocument78 pagesDifferential Equations: Introduction ToDaten YusfarinaNo ratings yet
- Integral Calculus - ExercisesDocument34 pagesIntegral Calculus - ExercisesVillamorchard0% (2)
- Integration Key FactsDocument7 pagesIntegration Key FactsAhmad Hussain100% (1)
- Integrales DoblesDocument7 pagesIntegrales DoblescarinasubiraNo ratings yet
- 5.integral Calculus Objectives:: DX DyDocument16 pages5.integral Calculus Objectives:: DX DyAndyMavia100% (1)
- IntegrationDocument8 pagesIntegrationapi-298592212No ratings yet
- Calculus NoteDocument95 pagesCalculus NoteAfeef Abu BakarNo ratings yet
- Chapter 6 (Integration Techniques) : DX X XDocument27 pagesChapter 6 (Integration Techniques) : DX X XArap DomNo ratings yet
- Tabular IntegrationDocument21 pagesTabular IntegrationArsalan JumaniNo ratings yet
- Unidad 1 Integrales Calculo Integral Valeria Casandra Rios Tellez ES1922027238 Raymundo Irineo Zanabria Salcedo LT-LCIN-2002-B1-001 24-07-2020Document6 pagesUnidad 1 Integrales Calculo Integral Valeria Casandra Rios Tellez ES1922027238 Raymundo Irineo Zanabria Salcedo LT-LCIN-2002-B1-001 24-07-2020Valeria CasandraNo ratings yet
- MATH26 M4 Applications Manguilimotan BSEDMath3ADocument11 pagesMATH26 M4 Applications Manguilimotan BSEDMath3ARetchel ManguilimotanNo ratings yet
- INTEGRAL CALCULUS HandoutsDocument7 pagesINTEGRAL CALCULUS Handoutsurfriend_jjn05No ratings yet
- Wang07 PDFDocument6 pagesWang07 PDFNandang Arif SaefulohNo ratings yet
- Knf1013 Week9 Differentiation Compatibility ModeDocument37 pagesKnf1013 Week9 Differentiation Compatibility ModeSyura PisyuNo ratings yet
- Worksheet 4.3 Integrating Special Functions: Section 1Document5 pagesWorksheet 4.3 Integrating Special Functions: Section 1atiggy05No ratings yet
- Common Practice Test - 5 Jee Mains: Matheamtics SolutionDocument7 pagesCommon Practice Test - 5 Jee Mains: Matheamtics Solutionblue_l1No ratings yet
- Unit 3. Integration: 3A. Differentials, Indefinite IntegrationDocument18 pagesUnit 3. Integration: 3A. Differentials, Indefinite IntegrationSantiago SeekerNo ratings yet
- Mathematics 1St First Order Linear Differential Equations 2Nd Second Order Linear Differential Equations Laplace Fourier Bessel MathematicsFrom EverandMathematics 1St First Order Linear Differential Equations 2Nd Second Order Linear Differential Equations Laplace Fourier Bessel MathematicsNo ratings yet
- Ten-Decimal Tables of the Logarithms of Complex Numbers and for the Transformation from Cartesian to Polar Coordinates: Volume 33 in Mathematical Tables SeriesFrom EverandTen-Decimal Tables of the Logarithms of Complex Numbers and for the Transformation from Cartesian to Polar Coordinates: Volume 33 in Mathematical Tables SeriesNo ratings yet
- Factoring and Algebra - A Selection of Classic Mathematical Articles Containing Examples and Exercises on the Subject of Algebra (Mathematics Series)From EverandFactoring and Algebra - A Selection of Classic Mathematical Articles Containing Examples and Exercises on the Subject of Algebra (Mathematics Series)No ratings yet
- Introductory Differential Equations: with Boundary Value Problems, Student Solutions Manual (e-only)From EverandIntroductory Differential Equations: with Boundary Value Problems, Student Solutions Manual (e-only)No ratings yet
- Chap 1 - Introduction To AccountingDocument27 pagesChap 1 - Introduction To AccountingMuhamad NazrinNo ratings yet
- Chapter 5 - Descriptive StatisticsDocument9 pagesChapter 5 - Descriptive StatisticsMuhamad NazrinNo ratings yet
- Chapter 6 - ProbabilityDocument9 pagesChapter 6 - ProbabilityMuhamad NazrinNo ratings yet
- Differentiation: SFM 1002 Mathematics II Chapter 2 DifferentiationDocument17 pagesDifferentiation: SFM 1002 Mathematics II Chapter 2 DifferentiationMuhamad NazrinNo ratings yet
- Maths - Social - Model Exam Grade 12Document9 pagesMaths - Social - Model Exam Grade 12Nebiyu100% (1)
- AMME3500 2013 Assignment 1Document5 pagesAMME3500 2013 Assignment 1JinDownloaderFree92No ratings yet
- Laboratory 3 Digital Filter DesignDocument8 pagesLaboratory 3 Digital Filter DesignModitha LakshanNo ratings yet
- Partial Differential Equations: The Wave EquationDocument19 pagesPartial Differential Equations: The Wave EquationArofah FaizaNo ratings yet
- Simulation of Process Scheduling Algorithm Using Poisson Distribution FunctionDocument11 pagesSimulation of Process Scheduling Algorithm Using Poisson Distribution FunctionJoshua50% (2)
- Basic Mathematics CPPDocument5 pagesBasic Mathematics CPPiWareNo ratings yet
- Scientific Computing With Case StudiesDocument399 pagesScientific Computing With Case Studiessnakesunny100% (1)
- Differentiation Optimization ProblemsDocument49 pagesDifferentiation Optimization ProblemsGeorgette DNo ratings yet
- Unit IDocument24 pagesUnit IPapithaNo ratings yet
- C Lab ProgramsDocument32 pagesC Lab ProgramsRAJ YNo ratings yet
- Mathematical Institute University of Oxford: Students' Guide Michaelmas Term 2009 Catherine WilkinsDocument67 pagesMathematical Institute University of Oxford: Students' Guide Michaelmas Term 2009 Catherine WilkinsscribdNo ratings yet
- Mathswatchworksheetsinterleavedq2ba UnlockedDocument362 pagesMathswatchworksheetsinterleavedq2ba Unlockedapi-223944181No ratings yet
- Grade 4 2nd QUARTER TESTDocument4 pagesGrade 4 2nd QUARTER TESTDenis CadotdotNo ratings yet
- NGEC 4 Final ExamDocument3 pagesNGEC 4 Final ExamJustiniano SalicioNo ratings yet
- Module 5 - Rational Functions Equations and InequalitiesDocument32 pagesModule 5 - Rational Functions Equations and InequalitiesSuzuri L100% (1)
- 10th Math Workbook PDFDocument292 pages10th Math Workbook PDFsuraj100% (2)
- Unit I Introduction: Mf7201 Optimization Techniques in ManufacturingDocument3 pagesUnit I Introduction: Mf7201 Optimization Techniques in ManufacturingCody LeeNo ratings yet
- Graph Regularized Non-Negative Matrix Factorization For Data RepresentationDocument14 pagesGraph Regularized Non-Negative Matrix Factorization For Data Representationavi_weberNo ratings yet
- Physics - Allum and Morris - Hodder 2023Document636 pagesPhysics - Allum and Morris - Hodder 2023Jathin Siddartha ReddyNo ratings yet
- A New Empirical Model For The Hydrocyclone Corrected EfficiencyDocument6 pagesA New Empirical Model For The Hydrocyclone Corrected EfficiencyTsakalakis G. Konstantinos100% (4)
- MTAP ReviewerDocument15 pagesMTAP ReviewerJULIUS COLLADONo ratings yet
- Why Phi - A Derivation of The Golden Mean Ratio Based On Heterodyne Phase ConjugationDocument7 pagesWhy Phi - A Derivation of The Golden Mean Ratio Based On Heterodyne Phase Conjugationpipul36No ratings yet
- The Kalman Fillter in GretlDocument12 pagesThe Kalman Fillter in GretlGuilhermeTomboloNo ratings yet
- The Mosers Formula For The Division of The CircleDocument12 pagesThe Mosers Formula For The Division of The Circlesamir anisNo ratings yet
- Indian Mathematicians and Their ContributionsDocument5 pagesIndian Mathematicians and Their ContributionsMukesh ChauhanNo ratings yet
- Quiz 01aaaae Floatingpoint AnswersDocument6 pagesQuiz 01aaaae Floatingpoint AnswersKim DavidNo ratings yet
- Markov Chains: Lecture 2Document4 pagesMarkov Chains: Lecture 2shahilshah1919No ratings yet
- 1 Theory of Convex FunctionsDocument14 pages1 Theory of Convex FunctionsLuis Carlos RojanoNo ratings yet
- Cambridge International Examinations: Read These Instructions FirstDocument19 pagesCambridge International Examinations: Read These Instructions FirstEKANEM KINGSLEY NSEOBONGNo ratings yet
- II PU Stats Most Important, Easy Questions & Formulae-2023 - 113150Document15 pagesII PU Stats Most Important, Easy Questions & Formulae-2023 - 113150aizak4814No ratings yet