Professional Documents
Culture Documents
Analytical and Numerical Modal Analysis of An Automobile Rear Torsion Beam Suspension
Uploaded by
Marco DanielOriginal Description:
Original Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Analytical and Numerical Modal Analysis of An Automobile Rear Torsion Beam Suspension
Uploaded by
Marco DanielCopyright:
Available Formats
15th International Conference on Experimental Mechanics
PAPER REF: 2747
ANALYTICAL AND NUMERICAL MODAL ANALYSIS OF AN
AUTOMOBILE REAR TORSION BEAM SUSPENSION
Marco Dourado1(*), Jos Meireles1
1
Mechanical Engineering Dept., University of Minho, Guimares, Portugal
(*)
Email: marcodanieldourado@hotmail.com
ABSTRACT
The aim of this paper is to present the vibrational analysis of a multi-DOF system,
representative of the torsion beam type suspension that equips some vehicles. The new
approach is to get the solution of the system, incorporating the effect of the torsion beam. The
natural frequencies i and mode shapes ui, are calculated analytically and numerically, freely
in space. The analytic results are compared with the numerical results obtained in the finite
element model developed. It is presented the mode shapes and natural frequencies of the
suspension system with and without torsion beam effect.
Keywords: torsion beam, torsion bar suspension system, multi-dof system
INTRODUCTION
The main functions of suspension system are to keep the vehicle tires in contact with the road,
support the weight of the vehicle, allow the vehicle to drive with stability and absorb the
forces generated by your movement, and provide comfort to passengers (Reza, 2008). When
the vehicle is moving, especially on uneven roads, forces are transmitted to the wheels with
vertical direction and which magnitude depends heavily of uneven pavement. The wheel thus
suffers a vertical acceleration.
In a torsion beam type suspension, the vertical displacement is transferred to the trailing arm,
which is rigidly connected to the torsion beam. The torsion beam is responsible for absorbing
energy that results from differences in effort between the two ends of the system. So this can
not only, guide the local system at each wheel, but also balance the effort involved on two
wheels when required with different loads.
The number of researches that study the interaction of torsion beam with the road vehicle is
very small. However, Jia et al (2006), make the behavior study of road vehicle in contact with
the deck surface, but dont applied the torsion bar in the system. Some studies of dynamics
analysis involving torsion bar suspension type, are applied to tracked vehicles, to evaluate the
ride performance, steerability, and stability on rough terrain (Yamakawa and Watanabe,
2004). Hohl (1986) study the influence of torsion beam in performance of tracked vehicle.
Murakami et al (1992), developed mathematical model which predicts spatial motion of
tracked vehicles on non-level terrain.
The our system is constituted by half body of a engine vehicle, assumed as a rigid mass m1, by
lateral mass moment inertia Iy and front mass moment inertia Ix as shown in Fig. 1. In this
new approach, a torsion beam is included in the system with stiffness constant kt, which,
together with the right and left wheel, constitutes the mass ((m2 + m3 ) 2 ) . As shown in later
Fig. 2, two springs with stiffness constant k1 and two shock absorbers with damping constant
c1, applied in n3-n6 and n4-n8 nodes, support the damped mass of the suspension system in the
linkage point one to the body vehicle, together with two other springs with stiffness constant
ICEM15
Porto/Portugal, 22-27 July 2012
k3 applied in n1-n5 and n2-n7 nodes, located in the other linkage point to the body vehicle. The
undamped mass is supported by two springs with stiffness constant k2 and two shock
absorbers with damping constant c2 applied in n5-n9, n7-n11, n6-n10 and n8-n12 nodes, that
represents the wheels.
To simulate the effect torsion beam, we applied kt values of same magnitude, in n3-n6, n4-n8,
n1-n5 and n2-n7 nodes, but with opposite signs. So, n3 n6 kt , n4 n8 kt , n1 n5 kt ,
n2 n7 kt . We attributed three different kt values, to get three different dynamic behaviors
in ours models.
We calculated natural frequencies i and mode shapes ui for the three models. These mode
shapes represent: the vertical displacement x, the body pitch and the body roll ; the vertical
displacement x1 and x3 of m2+m3 mass applied in n5 and n6 nodes, and the vertical
displacement x2 and x4 of m2+m3 mass applied in n7 and n8 nodes.
ANALYTICAL MODEL
As described in the previous point, for this system, shown in figure 1, it is assumed that the
system is undamped and natural frequencies are free in space. Then, the equation of motion
for the system under study is given by (Zienkiewicz, 1977):
..
[m] x + [k ]x = 0
a)
(1)
b)
c)
Fig. 1 Half car analytical model: a) right view; b) front view; c) left view
The equations that govern the movement of system shown in figure 1 are:
m1 x + k1 (x x1 d 1 + d 3 ) + k1 (x x 2 + d 2 + d 3 ) + k 3 (x x3 d1 d 4 ) +
..
+ k 3 (x x 4 + d 2 d 4 ) + k t (x x1 d 1 + d 3 ) k t (x x 2 + d 2 + d 3 )
k t ( x x 3 d 1 d 4 ) + k t ( x x 4 + d 2 d 4 ) = 0
(2)
I X d 1 k1 (x x1 d 1 + d 3 ) + d 2 k1 (x x 2 + d 2 + d 3 ) d 1 k 3 (x x 3 d 1 d 4 ) +
..
+ d 2 k 3 (x x 4 + d 2 d 4 ) d 1 k t (x x1 d 1 + d 3 ) d 2 k t (x x 2 + d 2 + d 3 ) +
(3)
d 1 k t ( x x 3 d 1 d 4 ) + d 2 k t ( x x 4 + d 2 d 4 ) = 0
I y + d 3 k1 ( x x1 d 1 + d 3 ) d 4 k 3 ( x x3 d 1 d 4 ) + d 3 k1 ( x x 2 + d 2 + d 3 )
..
d 4 k 3 ( x x 4 + d 2 d 4 ) + d 3 k t ( x x1 d 1 + d 3 ) d 3 k t ( x x 2 + d 2 + d 3 ) +
(4)
d 4 k t ( x x 3 d 1 d 4 ) d 4 k t ( x x 4 + d 2 d 4 ) = 0
Editors: J.F. Silva Gomes and Mrio A.P. Vaz
15th International Conference on Experimental Mechanics
m 2 x1 k1 (x x1 d 1 + d 3 ) k t (x x1 d 1 + d 3 ) + k 2 ( x1 y1 ) = 0
(5)
m 2 x 2 k1 (x x 2 + d 2 + d 3 ) + k t (x x 2 + d 2 + d 3 ) + k 2 ( x 2 y 2 ) = 0
(6)
m3 x3 k 3 (x x 2 d 1 d 4 ) + k t (x x3 d 1 d 4 ) + k 2 (x3 y1 ) = 0
(7)
m 3 x 4 k 3 ( x x 4 + d 2 d 4 ) k t ( x x 4 + d 2 d 4 ) + k 2 ( x 4 y 2 ) = 0
(8)
..
..
..
..
So, the equation (1) is express in matricial form by:
..
m1 0 0 0 0 0 0 x k11
..
0 I x 0 0 0 0 0 k 21
..
0 0 I Y 0 0 0 0 k 31
..
0 0 0 m 0 0 0 x + k
2
1 41
x..
m
0
0
0
0
0
0
2
2 k 51
..
0 0 0 0 0 m3 0 x3 k 61
..
0 0 0 0 0 0 m3 x4 k 71
k 26 k 27 x
k 36 k 37
0 0 x1 = 0
x
0 0 2
x3
k 66 0 x4
0 k 77
k12 k13 k14 k15 k16 k17
k 22 k 23 k 24 k 25
k 32 k 33 k34 k 35
k 42 k 43 k 44
k 52 k 53
k 55
k 62 k 63
k 72 k 73
(9)
where,
k11 = 2k1 + 2k 3
(10)
k12 = k 21 = d1 k1 + d 2 k1 d1k 3 + d 2 k 3
(11)
k13 = k31 = 2d 3 k1 2d 4 k3
(12)
k14 = k 41 = k1 k t
(13)
k15 = k 51 = k1 + k t
(14)
k16 = k 61 = k 3 + k t
(15)
k17 = k 71 k 3 k t
(16)
k 22 = d12 k1 + d 22 k1 + d12 k 3 + d 22 k 3
(17)
k 23 = k 32 = d1d 3 k1 + d1d 4 k 3 + d 2 d 3 k1 d 2 d 4 k 3 d1d 3 kt d1d 4 kt d 2 d 3 kt d 2 d 4 kt
(18)
k 24 = k 42 = d1 k1 + d1 k t
(19)
k 25 = k 52 = d 2 k1 + d 2 k t
(20)
k 26 = k 62 = d1 k 3 d1 k t
(21)
k 27 = k 72 = d 2 k 3 d 2 k t
(22)
ICEM15
Porto/Portugal, 22-27 July 2012
k 33 = 2d 32 k1 + 2d 42 k 3
(23)
k 34 = k 43 = d 3 k1 d 3 kt
(24)
k 35 = k53 = d 3 k1 + d 3 k t
(25)
k 36 = k 63 = d 4 k 3 d 4 k t
(26)
k 37 = k 73 = d 4 k 3 + d 4 kt
(27)
k 44 = k1 + k 2 + k t
(28)
k 55 = k1 + k 2 k t
(29)
k 66 = k 3 + k 2 k t
(30)
k 77 = k 3 + k 2 + k t
(31)
The natural frequencies i are obtained by determination of the eigenvalues square root i ,
of matrix [A ], that is calculating the determinative
det = [[A] I ] = 0
(32)
em que
[A] = [m]1 [k ]
(33)
i = i2
(34)
The modes shapes u i , are calculated determining the eigenvectors of matrix [A]
[[A] i I ]u i = 0
(35)
The table 1 presents the values associated with the variables envolved in the system. The
stifness constant kt assumes three diferente values. So we get three diferente models: model
without torsion beam system, with stifness constant kt = 0 N/m; model with torsion beam
system, with stifness constant kt = 25000 N/m; model with torsion beam system. with stiffness
constant kt = 75000 N/m.
Editors: J.F. Silva Gomes and Mrio A.P. Vaz
15th International Conference on Experimental Mechanics
Variable
d1
d2
d3
d4
k1
k2
k3
kt
Value
0.75
0.7
1.47
1.4
13000
200000
10000
0
25000
75000
Table 1 Variables of system
Units
Variable
m
m1
m
m2
m
m3
m
Ix
N/m
Iy
N/m
N/m
Value
840
33.8
32.2
147.2
576.63
Units
kg
kg
kg
kg.m2
kg.m2
N/m
Substituting the values of table 1, and with resource of MATLAB we solve the equations (33)
and (35) to the matrix system (9). The results are presented in the section Results.
NUMERICAL MODEL
The numerical model, as shown in figure 2, was constructed in ANSYS.
Fig. 2 Half car numerical model
The finite element model use three types of elements existents at the library of ANSYS: shell
elements (SHELL63), formed by n1, n2, n3 and n4 nodes, to represent the mass m1 of body;
mass elements (MASS 21), applied in n5, n6, n7 and n8 nodes, that represent the torsion beam
and wheels mass distributed in the system; combination elements (COMBIN 40) in n3-n6, n4ICEM15
Porto/Portugal, 22-27 July 2012
n8, n1-n5 and n2-n7 nodes, to represent the stiffness constant of springs and torsion beam, and
n5-n9, n7-n11, n6-n10 and n8-n12 nodes, to represent the stiffness constant of wheels.
ANALYTICAL RESULTS
Presents in this chapter the natural frequencies values analytically obtaind for the three
models with different kt values, and the respective modes shapes.
The eingenvalues of matrix [A] and natural frequencies for kt = 0 are, respectively:
1 = 50
2 = 154.8
3 = 158.1
4 = 6307.5
5 = 6309.8
6 = 6525.3
7 = 6526.3
1 = 50 = 7.07rad/s 1.13Hz
2 = 154.8 = 12.44rad/s 1.98Hz
3 = 158.1 = 12.57rad/s 2Hz
4 = 6307.5 = 79.42rad/s 12.65Hz
5 = 6309.8 = 79.43rad/s 12.65Hz
6 = 6525.3 = 80.78rad/s 12.86Hz
7 = 6526.3 = 80.79rad/s 12.86Hz
The eingenvalues of matrix [A] and natural frequencies for kt = 25000 are, respectively:
1 = 39.1
2 = 436.8
3 = 5568.1
4 = 5755.4
5 = 7092.5
6 = 7346.8
7 = 207.1
1 = 39.1 = 6.25rad/s 0.99Hz
2 = 436.8 = 20.90rad/s 3.33Hz
3 = 5568.1 = 74.62rad/s 11.88Hz
4 = 5755.4 = 75.86rad/s 12.08Hz
5 = 7092.5 = 84.22rad/s 13.41Hz
6 = 7346.8 = 85.71rad/s 13.65Hz
The eingnevalues of matrix [A] and natural frequencies for kt = 75000 are, respectively:
1 = 812.7
2 = 4191.5
3 = 4465.4
4 = 8693.8
5 = 9165.6
6 = 75.9
7 = 1220.4
1 = 812.7 = 28.50rad/s 4.54Hz
2 = 4191.5 = 64.74rad/s 10.31Hz
3 = 4465.4 = 20.90rad/s 10.64Hz
4 = 8693.8 = 93.24rad/s 14.85Hz
5 = 9165.6 = 95.74rad/s 15.24Hz
Although to be extracted seven eigenvalues for the trhee systems, nor all correspond to
natural frequencies, because these eigenvalues are negatives. For the case that kt = 0 N/m, we
have seven natural frequencies and seven mode shapes. For the case that kt = 25000 N/m only
six natural frequencies are considered, because the rotation aroun x axle and y axle, that is,
body roll e body pitch modes shapes, originate only one mode, the torsion mode
6
Editors: J.F. Silva Gomes and Mrio A.P. Vaz
15th International Conference on Experimental Mechanics
shape. For the case that kt = 75000 N/m only five natural frequencies are considered, because
the displacement x is anulled, and the body roll e body pitch modes shapes originate
only one mode, the torsion mode shape.
The eigenvectors of matrix [A] to kt = 0 N/m are:
+ 0.9946
- 0.0458
+ 0.1590
+ 0.0078
- 0.0869
+ 0.0118
- 0.7599
- 0.2114
+ 0.0625
+ 0.0077
- 0.6482
+ 0.9643
+ 0.0113
- 0.1269
- 0.1026
u1 = + 0.0018 u 2 = + 0.0046 u 3 = + 0.0079 u 4 = + 0.6404 u 5 = + 0.7576
+ 0.0020
- 0.0113
+ 0.0035
- 0.7651
+ 0.6342
+ 0.0021
+ 0.0085
- 0.0017
- 0.0157
+ 0.0078
+ 0.0023
- 0.0033
- 0.0050
+ 0.0131
+ 0.0114
+ 0.0654
- 0.0085
- 0.0506
- 0.0083
- 0.0968
+ 0.0128
u 6 = - 0.0163 u 6 = + 0.0073
+ 0.0121
+ 0.0127
- 0.6085
- 0.7872
+ 0.7915
- 0.6053
The figures 3 to 9, presents the modes shapes analytically obtained, for the model without
torsion beam, kt = 0 N/m. In the abcisses axle are represented the seven DOFs, where:
Point 1 is the first mode shape associated to the vertical displacement x;
Point 2 is the second mode shape associated to the body roll ;
Point 3 is the third mode shape associated to the body pitch ;
Point 4 is the fifth mode shape associated to the vertical displacement x1;
Point 5 is the fourth mode shape associated to the vertical displacement x2;
Point 6 is the seventh mode shape associated to the vertical displacement x3;
Point 7 is the sixth mode shape associated to the vertical displacement x4.
Fig. 1 1 mode shape
ICEM15
Fig. 4 2 mode shape
Porto/Portugal, 22-27 July 2012
Fig. 5 3 mode shape
Fig. 6 4 mode shape
Fig. 7 5 mode shape
Fig. 8 6 mode shape
Fig. 9 7 mode shape
The eigenvctors of matrix [A] to kt = 25000 N/m are:
Editors: J.F. Silva Gomes and Mrio A.P. Vaz
15th International Conference on Experimental Mechanics
0.9997
0.0335
+ 0.0659
+ 0.0777
0.1733
0.0182
+ 0.4495
+ 0.0411
0.0593
+ 0.1058
0.8920
+ 0.0868
0.1109
0.2071
0.0096
u1 = 0.0061 u 2 = 0.0265 u 3 = + 0.0023 u 4 = + 0.0033 u 5 = + 0.9473
+ 0.0004
+ 0.9928
0.0293
0.0018
+ 0.0028
+ 0.0005
+ 0.0289
+ 0.9886
0.0027
+ 0.0028
+ 0.0217
+ 0.0013
+ 0.0018
+ 0.1362
0.0060
+ 0.1191
+ 0.1223
0.2437
u 6 = + 0.1372
+ 0.0007
+ 0.0010
0.9448
The figures 10 to 15, presents the modes shapes analytically obtained, for the model wityh
torsion beam, kt = 25000 N/m. In the abcisses axle are represented the seven DOFs where the
second and third correspond to one DOF only. So:
Point 1 is the first mode shape associated to the vertical displacement x;
Point 2 e 3 is the second mode shape associated to the body pitch and body roll , that
is, torsion;
Point 4 is the fifth mode shape associated to the vertical displacement x1;
Point 5 is the third mode shape associated to the vertical displacement x2;
Point 6 is the fourth mode shape associated to the vertical displacement x3;
Point 7 is the sixth mode shape associated to the vertical displacement x4.
ICEM15
Fig. 10 1 mode shape
Fig. 11 2 mode shape
Fig. 12 3 mode shape
Fig. 13 4 mode shape
Porto/Portugal, 22-27 July 2012
Fig. 14 5 mode shape
Fig. 15 6 mode shape
The eigenvectors for the matrix [A] to kt = 75000 N/m are:
0.0052
+ 0.5176
+ 0.1247
+ 0.3635
- 0.1138
+ 0.4506
+ 0.0597
- 0.2670
- 0.1135
- 0.2653
+ 0.1410
- 0.5576
+ 0.2295
+ 0.5101
0.8899
u1 = 0.0522 u 2 = + 0.0136 u 3 = + 0.0019 u 4 = - 0.8120 u 5 = - 0.3436
+ 0.7189
+ 0.0024
- 0.4124
+ 0.0064
- 0.0012
+ 0.4377
0.0006
+ 0.6574
+ 0.0059
- 0.0016
+ 0.0469
+ 0.0105
+ 0.0029
- 0.3780
+ 0.7338
The figures 16 to 20, presents the modes shapes analytically obtained, for the model wityh
torsion beam, kt = 75000 N/m. In the abcisses axle are represented the seven DOFs where the
first is annulled, and the second and third correspond to one DOF only. So:
Point 2 e 3 is the first mode shape associated to the body pitch and body roll , that is,
torsion;
Point 4 is the fourth mode shape associated to the vertical displacement x1;
Point 5 is the second mode shape associated to the vertical displacement x2;
Point 6 is the third mode shape associated to the vertical displacement x3;
Point 7 is the fifth mode shape associated to the vertical displacement x4.
Fig. 16 1 mode shape
10
Fig. 17 2 mode shape
Editors: J.F. Silva Gomes and Mrio A.P. Vaz
15th International Conference on Experimental Mechanics
Fig. 18 3 mode shape
Fig. 19 4 mode shape
Fig. 20 5 mode shape
NUMERICAL RESULTS
The natural frequencies and mode shapes numerically obtained are presented in table 2.
Table 2 Numerical natural frequencies and mode shapes for different kt values
kt
1
2
3
4
5
6
7
(N/m)
(Hz)
(Hz)
(Hz)
(Hz)
(Hz)
(Hz)
(Hz)
Without
1.12
1.97
1.98
12.63 12.64 12.85 12.86
Torsion
Beam
body
disp.
disp.
disp.
disp.
disp.
body
Mode
pitch x1 and x1 and x3 and x3 and
x
roll
Shape
x2
x2
x4
x4
With
+25000
0.92
3.29
11.87 12.06 13.32
13.6
Torsion
-25000
Beam
body roll
disp.
disp.
disp.
disp.
disp.
Mode
and body pitch x2 and x2 and x1 and x1 and
x
Shape
(torsion)
x3
x3
x4
x4
With
+75000
4.50
9.98
10.58 14.30 15.07
Torsion
-75000
Beam
body roll
disp.
disp.
disp.
disp.
Mode
and body pitch x2 and x2 and x1 and x1 and
Shape
(torsion)
x3
x3
x4
x4
The table 3 and table 4, present respectively, the comparison between the natural frequencies
and mode shapes analytically and numerically calculated. The values obtained using the two
methods, numerical and analytical, are very concordant, and the numerical models confirm
the analytical models.
ICEM15
11
Porto/Portugal, 22-27 July 2012
Table 3 Comparison between the natural frequencies obtained using the two methods
Without
With
With
Torsion
Torsion
Torsion
Beam
Beam
Beam
+25000
+75000
kt (N/m)
kt (N/m)
kt (N/m)
-25000
-75000
Analytical Numerical Analytical Numerical
Analytical Numerical
Model
Model
Model
Model
Model
Model
1.13
1.12
0.99
0.92
4.54
4.50
1 (Hz)
1.98
1.97
3.33
3.29
10.31
9.98
2 (Hz)
2
1.98
11.88
11.87
10.64
10.58
3 (Hz)
12.65
12.63
12.08
12.06
14.85
14.30
4 (Hz)
12.65
12.64
13.41
13.32
15.24
15.07
5 (Hz)
12.86
12.85
13.65
13.6
6 (Hz)
12.86
12.86
7 (Hz)
Mode
Shapes
1st
2nd
3rd
4th
5th
6th
7th
Table 4 Comparison between the mode shapes obtained using the two methods
With
With
Without
Torsion
Torsion
Torsion
Beam
Beam
Beam
+25000
+75000
kt (N/m)
kt (N/m)
kt (N/m)
-25000
-75000
Analytical
Numerical
Analytical
Numerical
Analytical
Numerical
Model
Model
Model
Model
Model
Model
disp. x
disp. x
disp. x
disp. x
body roll
body roll
body roll
body roll
body roll
body roll
and body pitch and body pitch and body pitch and body pitch
body pitch
body pitch
(torsion)
(torsion)
(torsion)
(torsion)
disp. x1
disp. x1 and x2
disp. x2
disp. x2 and x3
disp. x2
disp. x2 and x3
disp. x2
disp. x1 and x2
disp. x3
disp. x2 and x3
disp. x3
disp. x2 and x3
disp. x3
disp. x3 and x4
disp. x1
disp. x1 and x4
disp. x1
disp. x1 and x4
disp. x4
disp. x3 and x4
disp. x4
disp. x1 and x4
disp. x4
disp. x1 and x4
CONCLUSION
Depending on the increase of stiffness constant value kt of torsion beam, for constant values
k1, k2 and k3, the natural frequencies that influence the vertical displacement x tend to decrease
or disappear. The body roll and the body pitch become a torsion mode shape when the
torsion beam is incorporated in the system. The fourth and fifth natural frequency value, both
associated with the vertical movement x2 and x3 of the undamped mass, decrease by increasing
kt value.
The natural frequencies and mode shapes values analytically calculated, confirm the values
numerically obtained, so the new method to represent the torsion beam effect is reliable.
ACKNOWLEDGMENTS
The authors gratefully acknowledge the Centre for Mechanical and Materials Technologies
(Centro de Tecnologias Mecnicas e de Materiais CT2M) and QREN.
12
Editors: J.F. Silva Gomes and Mrio A.P. Vaz
15th International Conference on Experimental Mechanics
REFERENCES
Hohl G.H. Torsion-Bar Spring and Damping Systems of Tracked Vehicles. Journal of
Terramechanics, Vol. 22, N 4, pp. 195-203, 1986.
Jia J., Ulfvarson A. Dynamic Analysis of Vehicle-Deck Interactions. Ocean Engineering, Vol.
33, pp. 1765-1795, 2006.
Murakami H., Watanabe K., Kitano M. A Mathematical Model for Spatial Motion of Tracked
Vehicles on Soft Ground. Journal of Terramechanics, Vol. 29, N 1, pp 71-81, 1992.
Reza NJ. Vehicle Dynamics: Theory and Application. Springer, New York, 2008, p. 827-881.
Yamakawa J., Watanabe K. A Spatial Motion Analysis Model of Tracked Vehicles with
Torsion Bar Type Suspension. Journal of Terramechanics, Vol. 41, pp. 113-126, 2004.
Zienkiewicz OC. The Finite Element Method in Engineering Science, McGraw-Hill
Publishing Company, London, United Kingdom, 1977.
ICEM15
13
You might also like
- Vibration and Control: Associate Professor Department of Mechanical Engineering Y.T.UDocument82 pagesVibration and Control: Associate Professor Department of Mechanical Engineering Y.T.Udora901No ratings yet
- ME4213 Tutorial 2aDocument4 pagesME4213 Tutorial 2aLinShaodun100% (1)
- Inverted Pendulum 1Document21 pagesInverted Pendulum 1ricardoxcmNo ratings yet
- Development of An Automated Storage/Retrieval System: Chung Tan Lam, Nguyen Tuong Long, Phan Hoang Phung, Le Hoai QuocDocument18 pagesDevelopment of An Automated Storage/Retrieval System: Chung Tan Lam, Nguyen Tuong Long, Phan Hoang Phung, Le Hoai QuoctieuboilangthangkyNo ratings yet
- Natural Freq and Modal ShapesDocument5 pagesNatural Freq and Modal ShapesHelen HerodicoNo ratings yet
- 210 Nice Symmetric InequalitiesDocument7 pages210 Nice Symmetric InequalitiesswapnilNo ratings yet
- PEME200001 Mathematical Techniques 2Document10 pagesPEME200001 Mathematical Techniques 2Andrew AndersonNo ratings yet
- 1 Vibration Analysis Using MATLABDocument26 pages1 Vibration Analysis Using MATLABreachspk100% (1)
- SLAM of Multi-Robot System Considering Its Network Topology: H. W. Dong, Z. W. LuoDocument2 pagesSLAM of Multi-Robot System Considering Its Network Topology: H. W. Dong, Z. W. LuopaperopenaccessNo ratings yet
- 10 - SHM, Springs, DampingDocument4 pages10 - SHM, Springs, DampingBradley NartowtNo ratings yet
- Vib QN Paper Test IIDocument4 pagesVib QN Paper Test IIRaghupathi ManickamNo ratings yet
- NFNMS 5Document87 pagesNFNMS 5wanpudinNo ratings yet
- Applied CalculusDocument12 pagesApplied CalculusRonald MulindeNo ratings yet
- PDFDocument7 pagesPDFAliOucharNo ratings yet
- Mechanical Vibration Solved ExamplesDocument84 pagesMechanical Vibration Solved ExamplesKajal Khan100% (2)
- Truss MathematicsDocument8 pagesTruss MathematicsOladunni Afolabi100% (1)
- 2413, Practice Exam 3, FA14Document5 pages2413, Practice Exam 3, FA14Matthew LuNo ratings yet
- 3 Story Seismic AnalysisDocument15 pages3 Story Seismic AnalysisKavita Kaur KamthekarNo ratings yet
- Mechanical Engineering Full Paper 2006Document20 pagesMechanical Engineering Full Paper 2006Raghib ShakeelNo ratings yet
- Modal AnalysisDocument40 pagesModal AnalysisSumit Thakur100% (1)
- DocumentDocument9 pagesDocumentDavid RodriguezNo ratings yet
- A Review of Dynamic Models Used in Simulation of Gear TransmissionsDocument10 pagesA Review of Dynamic Models Used in Simulation of Gear TransmissionsKhalid F AbdulraheemNo ratings yet
- 1006 0351 PDFDocument54 pages1006 0351 PDFRemyan RNo ratings yet
- Mechanical Vibration Solved ExamplesDocument92 pagesMechanical Vibration Solved ExamplesZain Ahmed85% (13)
- The Analysis of The Global Ship Strengths in Vertical Plane With 3D-Fem Hull ModelsDocument22 pagesThe Analysis of The Global Ship Strengths in Vertical Plane With 3D-Fem Hull ModelsMihaela NidelcuNo ratings yet
- Discrete-Time Nonlinear Sliding Mode Controller: Nikhil Kumar Yadav, R.K. SinghDocument7 pagesDiscrete-Time Nonlinear Sliding Mode Controller: Nikhil Kumar Yadav, R.K. SinghHamza MasreNo ratings yet
- Chap3 2bDocument6 pagesChap3 2bAl- DhaheriNo ratings yet
- 2.4 The Chain RuleDocument2 pages2.4 The Chain Rulemasyuki1979No ratings yet
- Piecewise Cubic Splines: HAP Urve IttingDocument12 pagesPiecewise Cubic Splines: HAP Urve IttingSankar RoyNo ratings yet
- Mathematical Modeling of Mechanical Systems and Electrical SystemsDocument49 pagesMathematical Modeling of Mechanical Systems and Electrical SystemsMary DunhamNo ratings yet
- Vibprobset 04Document3 pagesVibprobset 04Aybek AhmetoğluNo ratings yet
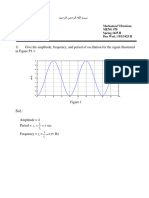
- 1) Give The Amplitude, Frequency, and Period of Oscillation For The Signal Illustrated in Figure P1.1Document8 pages1) Give The Amplitude, Frequency, and Period of Oscillation For The Signal Illustrated in Figure P1.1Ahmed Abdulbary AL-QarmNo ratings yet
- Dynamics Tutorial 14-Natural Vibrations-One Degree of Freedom-27p PDFDocument13 pagesDynamics Tutorial 14-Natural Vibrations-One Degree of Freedom-27p PDFmanfredm6435No ratings yet
- Truss Matlab Mef StifnessDocument8 pagesTruss Matlab Mef StifnessAoun Omar100% (1)
- Inverse Kinematics Problem (Ikp) of 6-Dof Manipulator by Locally Recurrent Neural Networks (LRNNS)Document5 pagesInverse Kinematics Problem (Ikp) of 6-Dof Manipulator by Locally Recurrent Neural Networks (LRNNS)yousif al mashhadanyNo ratings yet
- NSEJS Solution (Code-578) .Document6 pagesNSEJS Solution (Code-578) .Yatish GoyalNo ratings yet
- Example From CH 1 To CH 6Document21 pagesExample From CH 1 To CH 6SteveNo ratings yet
- 4500ICBTEGDocument9 pages4500ICBTEGKalana wickramanayakaNo ratings yet
- Cive162001 2006 Brief SolutionsDocument7 pagesCive162001 2006 Brief Solutionssjeyarajah21No ratings yet
- Modeling and Vibration AnalysisDocument11 pagesModeling and Vibration AnalysisRowdyRaheel100% (1)
- Chapter-6: Energy Method (Lagrange's Method)Document35 pagesChapter-6: Energy Method (Lagrange's Method)ideepujNo ratings yet
- 07 - Rotational Kinematics and MechanicsDocument9 pages07 - Rotational Kinematics and MechanicsBradley NartowtNo ratings yet
- Lab2 Expt1Document2 pagesLab2 Expt1Sureil GupteNo ratings yet
- Fre Sers Sws Moving SensorsDocument24 pagesFre Sers Sws Moving SensorshenrydclNo ratings yet
- Integral Calculus - ExercisesDocument34 pagesIntegral Calculus - ExercisesVillamorchard0% (2)
- Response Spectrum Analysis PDFDocument30 pagesResponse Spectrum Analysis PDFSujay SantraNo ratings yet
- Single Axis Text I J Mic 08075 FinalDocument26 pagesSingle Axis Text I J Mic 08075 Finalali almorsedNo ratings yet
- May 2011 Board Exam All SubjectsDocument10 pagesMay 2011 Board Exam All SubjectsNarcisa Rudnic86% (14)
- Chapter 2 Kinematics 1DDocument46 pagesChapter 2 Kinematics 1Dnicky1213aNo ratings yet
- Vibration of Two Degree of Freedom SystemDocument23 pagesVibration of Two Degree of Freedom SystemDewa Ayu Mery AgustinNo ratings yet
- Logical progression of twelve double binary tables of physical-mathematical elements correlated with scientific-philosophical as well as metaphysical key concepts evidencing the dually four-dimensional basic structure of the universeFrom EverandLogical progression of twelve double binary tables of physical-mathematical elements correlated with scientific-philosophical as well as metaphysical key concepts evidencing the dually four-dimensional basic structure of the universeNo ratings yet
- Ten-Decimal Tables of the Logarithms of Complex Numbers and for the Transformation from Cartesian to Polar Coordinates: Volume 33 in Mathematical Tables SeriesFrom EverandTen-Decimal Tables of the Logarithms of Complex Numbers and for the Transformation from Cartesian to Polar Coordinates: Volume 33 in Mathematical Tables SeriesNo ratings yet
- Factoring and Algebra - A Selection of Classic Mathematical Articles Containing Examples and Exercises on the Subject of Algebra (Mathematics Series)From EverandFactoring and Algebra - A Selection of Classic Mathematical Articles Containing Examples and Exercises on the Subject of Algebra (Mathematics Series)No ratings yet
- Analytical Modeling of Solute Transport in Groundwater: Using Models to Understand the Effect of Natural Processes on Contaminant Fate and TransportFrom EverandAnalytical Modeling of Solute Transport in Groundwater: Using Models to Understand the Effect of Natural Processes on Contaminant Fate and TransportNo ratings yet
- Robot Manipulators: Modeling, Performance Analysis and ControlFrom EverandRobot Manipulators: Modeling, Performance Analysis and ControlNo ratings yet
- O level Physics Questions And Answer Practice Papers 2From EverandO level Physics Questions And Answer Practice Papers 2Rating: 5 out of 5 stars5/5 (1)
- Difference Equations in Normed Spaces: Stability and OscillationsFrom EverandDifference Equations in Normed Spaces: Stability and OscillationsNo ratings yet
- 10 Impedance TubeDocument17 pages10 Impedance TubeMarco DanielNo ratings yet
- Development of Reduced Finite Element Models of Structures For Application To Road VehiclesDocument11 pagesDevelopment of Reduced Finite Element Models of Structures For Application To Road VehiclesMarco DanielNo ratings yet
- 3D Truss AnalysisDocument5 pages3D Truss AnalysisMarco DanielNo ratings yet
- Design of An Acoustic Anechoic Chamber For Application in Hearing Aid REsearchDocument6 pagesDesign of An Acoustic Anechoic Chamber For Application in Hearing Aid REsearchJude SudarioNo ratings yet
- Curriculum Vitae-Col DR D S GrewalDocument13 pagesCurriculum Vitae-Col DR D S GrewalAvnish Kumar ThakurNo ratings yet
- Chapter IDocument54 pagesChapter IDila SoulvibeNo ratings yet
- Why Should I Hire You - Interview QuestionsDocument12 pagesWhy Should I Hire You - Interview QuestionsMadhu Mahesh Raj100% (1)
- The Life Cycle of A Butterfly Lesson PlanDocument2 pagesThe Life Cycle of A Butterfly Lesson Planst950411No ratings yet
- Yes, Economics Is A Science - NYTimes PDFDocument4 pagesYes, Economics Is A Science - NYTimes PDFkabuskerimNo ratings yet
- Edmund Dulac, W B Yeats and The MagiDocument23 pagesEdmund Dulac, W B Yeats and The MagiRaphael888No ratings yet
- Clinical Implications of Adolescent IntrospectionDocument8 pagesClinical Implications of Adolescent IntrospectionJoshua RyanNo ratings yet
- College Graduation SpeechDocument2 pagesCollege Graduation SpeechAndre HiyungNo ratings yet
- Valencia & Roxas Income Taxation - IndividualsDocument12 pagesValencia & Roxas Income Taxation - IndividualsJonathan Junio100% (1)
- PI 041 1 Draft 3 Guidance On Data Integrity 1Document52 pagesPI 041 1 Draft 3 Guidance On Data Integrity 1Yolanda PerezNo ratings yet
- Patient Autonomy and RightDocument24 pagesPatient Autonomy and RightGusti Ngurah Andhika P67% (3)
- Nieva Vs DeocampoDocument5 pagesNieva Vs DeocampofemtotNo ratings yet
- Enhancing The Value of Urban Archaeological SiteDocument53 pagesEnhancing The Value of Urban Archaeological SitePaul VădineanuNo ratings yet
- Roles and Competencies of School HeadsDocument3 pagesRoles and Competencies of School HeadsPrincess Pauline Laiz91% (23)
- Phil KnightDocument14 pagesPhil KnightJon Snow0% (1)
- Work Motivation & Job Design (Lec. 6, Chap. 7) - UPDATED2Document14 pagesWork Motivation & Job Design (Lec. 6, Chap. 7) - UPDATED2AnnasNo ratings yet
- Social Science 1100: Readings in Philippine History: Instructional Module For The CourseDocument15 pagesSocial Science 1100: Readings in Philippine History: Instructional Module For The CourseXynNo ratings yet
- Lesson Plan The Mountain That Loved A BIRD by Sheena E. BernalDocument6 pagesLesson Plan The Mountain That Loved A BIRD by Sheena E. BernalSheEna Brnl100% (1)
- Waiting For GodotDocument9 pagesWaiting For GodotKNo ratings yet
- 1956-Chayes. - Petrographic Modal AnalysisDocument120 pages1956-Chayes. - Petrographic Modal AnalysisdmsanchezcNo ratings yet
- Kuk YogaDocument14 pagesKuk YogaVijay KumarNo ratings yet
- Math LogicDocument44 pagesMath LogicJester Guballa de Leon100% (1)
- The Book of Alignment (Updated)Document165 pagesThe Book of Alignment (Updated)Max KlostermannNo ratings yet
- Under Down UnderDocument698 pagesUnder Down Underttreks100% (3)
- The Kriya Yoga PracticesDocument11 pagesThe Kriya Yoga PracticesTushar Naik100% (46)
- The Right Way To Manage ExpatsDocument2 pagesThe Right Way To Manage ExpatsShayne RebelloNo ratings yet
- Compensation: Third Canadian Edition Milkovich, Newman, ColeDocument28 pagesCompensation: Third Canadian Edition Milkovich, Newman, ColeNeha AgarwalNo ratings yet
- Rizal PresentationDocument54 pagesRizal PresentationValiant BaybayNo ratings yet
- If Poem Worksheet PDFDocument12 pagesIf Poem Worksheet PDFRaniaGF100% (2)
- Introduction To Game Theory: Matigakis ManolisDocument46 pagesIntroduction To Game Theory: Matigakis ManolisArmoha AramohaNo ratings yet