Professional Documents
Culture Documents
TrigandBearings ExercisesSolutions
Uploaded by
Mab DTOriginal Description:
Original Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
TrigandBearings ExercisesSolutions
Uploaded by
Mab DTCopyright:
Available Formats
WWW.C E M C .U WAT E R LO O.
C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
Mathematics Teachers Enrichment Program
MTEP 2012
Trigonometry and Bearings
Solutions to Exercises
= 90 , AB = 8 and BC = 15. Solve 4ABC.
1. In 4ABC, ABC
Round side length and angles to one decimal, as necessary.
!
'
Solution:
Let b represent the length of side AC.
Using Pythagoras Theorem, b2 = 82 + 152 = 289 and b = 17
follows.
"
%&
= tan C = 8 =0.5333
Using basic trigonometry, tan ACB
and C = 28.1 .
15
= A = 180 90 28.1 = 61.9 .
Since the angles in a triangle add to 180 , BAC
= 28.1 , BAC
= 61.9 and |AC| = 17.
Therefore ACB
= 90 , XY
Z = 41 , and XY = 20. Round side lengths to one deci2. Solve 4XY Z, given XZY
mal, as necessary.
&
Solution:
Let x represent the length of side ZY and y represent the length
of side XZ.
Since the angles in a triangle add to 180 ,
=X
= 180 90 41 = 49 .
ZXY
y
and
Using basic trigonometry, sin 41 = 20
y = 20 sin 41 =
13.1 follows.
'
!"
"
$%
Using Pythagoras Theorem, x2 = 202 13.122 = 227.83. x =
15.1 follows. You could also use
x
basic trigonometry here again. cos 41 = 20
and x = 20 cos 41 =
15.1 follows.
= 49 , |ZY | = 15.1 and |XZ| = 13.1.
Therefore ZXY
3. At a point 50 m from the base of a tower the angle of elevation to the top of the tower is 70 .
Determine the height of the tower, to the nearest metre.
Solution:
Let h represent the height of the tower, in m.
h
50
h = 50 tan 70
Using basic trigonometry, tan 70 =
h =
137.4
Therefore, to the nearest metre, the height of the tower is 137 m.
"#
!"#$
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
4. From the top of a 40 m tower, an observer measures the angle of depression to a boat in the
water below to be 28 . How far, to the nearest metre, is the boat from the base of the tower?
Solution:
Let d represent the distance, in m, from the bottom of the tower to the boat. Let represent
the angle of elevation from the boat to the top of the tower. Therefore = 28 . (The angle of
elevation from the boat to the top of the tower equals the angle of depression from the top of the
tower to the boat.)
%&
!"#$
Using basic trigonometry,
tan 28 =
40
40
and d =
=
75.2 m follows.
d
tan 28
Therefore, to the nearest metre, the boat is 75 m out from the bottom of the tower.
5. A 12.4 m flagpole is placed on top of a tall building. An observer, standing directly in front of the
building and flagpole, measures the angle of elevation to the bottom of the flagpole to be 42.5
and to the top of the flagpole to be 48.2 . Determine the height of the building, to the nearest
metre.
Solution:
Represent the given information on a diagram. Let the height of the building be h and the
distance out from the building to the observer be d.
In 4BCD, hd = tan 42.5 and in 4ACD, h+12.4
= tan 48.2 . Rearranging, h = d(tan 42.5 ) and
d
"
h + 12.4 = d(tan 48.2 ). Substitute for h in the second equation,
&"#!'(
d(tan 42.5 ) + 12.4 = d(tan 48.2 )
#
12.4 = d(tan 48.2 ) d(tan 42.5 )
12.4 = d(tan 48.2 tan 42.5 )
12.4 (tan 48.2 tan 42.5 ) = d
!%#"
61.35 =
d
!"#$
But h = d(tan 42.5 ) =
56.2
&
Therefore the height of the building is 56 m.
'
6. To calculate the height of a tower, David measured the angle of elevation
of the top of the tower from a point A to be 42 . He then moved 30 m
closer to the tower and from point B measured the angle of elevation to
the top of the tower to be 50 . To the nearest metre, determine the height
of the tower.
Solution:
#$ +,&
! !"#$ "
and T BC
form a straight angle. Therefore ABT
= 180 50 = 130 .
ABT
The angles in a triangle add to 180 so in 4T BA, AT B = 180 42 130 = 8 .
Let x represent the length of side BT and h represent T C, the required height.
Using the Sine Rule in 4ABT ,
Then in 4T BC,
h
x
x
sin 42
30
sin 8
and x =
= sin 50 and h = x sin 50 =
110
The height of the tower is 110 m.
30 sin 42
sin 8
=
144.24.
%&
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
7. Determine the length of BC in 4ABC where AB = 10, AC = 9 and
= 58 . Round correctly to one decimal place.
BAC
!"
!"
Solution:
The diagram to represent the problem is shown to the right. Using the
Cosine Rule, |BC|2 = 102 + 92 2 10 9 cos 58 =
85.61 and |BC| =
9.3.
$
!
8. Determine the size of the largest angle in 4P QR where P Q = 9, QR = 15
and P R = 11. Round correctly to one decimal place.
""
Solution:
The largest angle will be opposite the largest side. Therefore we are required to find P .
92 + 112 152
Using the Cosine Rule, cos P =
=
0.1162 and P =
96.7 .
2(9)(11)
"
"#
Z = 43 , XZY
9. In 4XY Z, XY
= 73 and Y Z = 25. Solve 4XY Z,
rounding correctly to one decimal place.
$!
Solution:
Since two angles in the triangle are known, the third angle is easily found.
= 180 43 73 = 64 .
X
!"
"
#"
%&
z
y
25
=
=
.
sin 73
sin 43
sin 64
25 sin 43
25 sin 73
=
26.6
and
y
=
=
19.0.
It follows that z =
sin 64
sin 64
Using the Sine Rule,
10. In 4DEF , DE = 9.4, EF = 17.5 and DF = 12.8.
rounding each angle to one decimal place.
Solve 4DEF .
Solution:
!
$%"&
!"#
The diagram to represent the information from the problem is shown to
2
2
2
"
$'"(
= 12.8 + 9.4 17.5 =
0.2246
the right. Using the Cosine Rule, cos D
2 12.8 9.4
=
and D
103.0 .
sin F
sin 103.0
9.4 sin 103.0
Using the Sine Rule,
=
. Then sin F =
=
0.5234 and F =
31.6 .
9.4
17.5
17.5
= 180 103.0 31.6 = 45.4 .
It follows that E
= 103.0 , E
= 45.4 , and F = 31.6 .
Therefore, D
11. A triangular piece of land is bounded by 32 m of brick wall, 50 m of
fencing and 28 m of road along the front. What angle does the fence make
with the road?
Solution:
Represent the given information on the diagram. We are looking for C.
2
2
2
50 + 28 32
Using the Cosine Rule, cos C =
=
0.8071 and C =
36.2 .
2 50 28
Therefore, the fence meets the road at a 36 angle.
!
!"#$
,-./-
'%#$
0*11
"
%&#$
()*+
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
"
12. Determine the length of x to one decimal place.
Solution:
Let y represent the length of BD.
y
= sin 40 , y = 30 sin 40 =
19.3.
In 4CBD,
30
y
In 4ABD, = cos 35 , x = y cos 35 =
23.5.
x
#
!
&
!#$#%&
!"
%
'#
Therefore the length of x is 23.5 units.
13. The bearing from A to B is 160 . What is the bearing from B to A?
!"#
Solution:
"
= 160 represents
Represent the given information on the diagram. P AB
the bearing from A to B. We want the bearing from B to A and therefore
want to find reflex angle ABQ.
= 180 P AB
= 180 160 = 20 . Reflex angle
P A k QB so ABQ
ABQ = 360 20 = 340 . Therefore the bearing from B to A is 340 .
14. From an observation point in a fire tower, the observer spots a fire 5 km
away at a bearing 130 . The observer also spots a village 2 km away on a
bearing 240 . How far is the fire away from the village?
Solution:
Represent the given information on the diagram.
#
$
$&'( !
F =
NT
is the bearing from the tower to the fire.
N T V = 240 is the bearing from tower to the village.
Then V T F = 240 130 = 110 .
130
$%#
!"#
!!#
)&'(
%
"
Let x represent the distance from the village to the fire. Therefore x = |V F |.
By the Cosine Rule, x2 = 22 + 52 2(2)(5)cos 110 =
35.84 and x =
6.0 km.
The distance from the fire to the village is 6.0 km.
15. A hiker walks 1.5 km on a bearing 035 . At this point he turns directly south
and walks 3.5 km. How far and on what bearing must he walk to return to
his original starting point?
'"#$%&
Solution:
Represent the given information on the diagram.
= 35 is the bearing for the 1.5 km part of the hike, shown as A to B.
P AB
Then the hiker turns south and goes 3.5 km to C. Therefore P A k BC and
= P AB
= 35 follows.
ABC
Let x represent the distance from C to the original start point at A.
!#
!#
!"#$%&
"
%
By the Cosine Rule, x2 = 1.52 + 3.52 2(1.5)(3.5)cos 35 =
5.90 and x =
2.4 km.
sin C
sin 35
1.5 sin 35
=
. Then sin C =
=
0.3542 and C =
20.7 .
1.5
x
x
The required bearing is 360 20.7 =
339.3 .
Using the Sine Rule,
The hiker must walk about 2.4 km on a bearing of 339 to get to the original start point.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
!
%&'(
16. Two ships, R and Q, left a port, P , at the same time.
After two hours, R had travelled 8 km on a bearing
075 from port and Q had travelled 10 km on a bearing
305 from port. How far apart are the two ships after
two hours?
"
%"&'(
##
$#
)&'(
!"#
Solution:
Let x represent the distance between the two boats after 2 hours. Represent the given information on the diagram.
R = 75 is the bearing from P to R. Reflex angle N P
Q = 305 is the bearing from P to Q.
NP
Q = 360 305 = 55 and QP
R = 55 + 75 = 130 .
Then N P
By the Cosine Rule, x2 = 102 + 82 2(10)(8)cos 130 =
266.85 and x =
16.3 km.
The ships are 16.3 km apart after two hours.
17. A tour boat leaves port and travels 15 km on a bearing
of 088 and then travels a further 24 km on a bearing
of 145 . The boat then returns directly to the starting
point. Determine the distance to the port and the bearing
along which the tour boat must travel.
$
!
!!
Solution:
"
"$&'(
"#$
!!
'
%$
)#&'(
Let x represent the distance the tour boat must travel
to return to port. Represent the given information on
the diagram. Other information on the diagram will be
justified below.
%$
&
#
= AP Q = 88 .
AP Q = 88 is the bearing from the port for 15 km. AP k BD so P QD
= 145 is the bearing for the 24 km part of the tour. BQD is a straight line so
BQR
= DQR
= 35 .
= 180 145 = 35 . CR k BD so QRC
DQR
= P QD
+ DQR
= 88 + 35 = 123 .
P QR
Using the Cosine Rule, x2 = 152 + 242 2(15)(24) cos 123 =
1193.14 and x =
34.5.
sin P RQ
sin 123
= 15 sin 123 =
=
Using the Sine Rule,
=
and sin P RQ
0.3642. Then P RQ
21 .
15
x
x
= 360 P RQ
QRC
=
The required bearing is the reflex angle CRP
360 21 35 = 304 .
The tour boat must travel 34.5 km on a bearing of 304 to return to the port.
+ !"#$%&'()*
18. Two towns, A and B, lie on longitude 37 W. Their latitudes are
50.4 N and 72.6 N, respectively. Calculate the shortest distance
between the two towns.
Solution:
The sector angle is = 72.6 50.4 = 22.2 .
$-4708 +234 56#
"-./01 +234 56#
!
The distance from A to B along longitude 37 W is
22.2
2r =
40 000 =
2 470 km, to three significant figures.
360
360
,
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
19. Two towns, C and D, lie on the same longitude. Their latitudes
are 80 N and 70 S, respectively. Calculate the shortest distance
between the two towns.
+ !"#$%&'()*
"-./ +0#
Solution:
!
The sector angle is found by adding the two latitudes
= 80 + 70 = 150 .
The distance from C to D along the same longitude is
$-1/ ,0#
150
2r =
40 000 =
16 700 km, to three significant figures.
360
360
20. Two cities, A and B, lie on the Equator, one at longitude 65 E
and the other at longitude 23 W. Calculate the distance between
the two towns, measured along the Equator.
+ !"#$%&'()*
Solution:
The sector angle is found by adding the two longitudes
= 65 + 23 = 88 .
The distance from A to B along the Equator is
88
2r =
40 000 =
9 780 km, to three significant figures.
360
360
21. Find the distance, measured along a meridian, from any point on
parallel of latitude 30 N to the North Pole.
01
45
"-. +/01 23#
$-. +/45 63#
+ !"#$%&'()*
-1/ +0#
"-./ +0#
Solution:
The sector angle is found by subtracting the latitude from 90
giving 60 .
The distance measured along any meridian is
60
2r =
40 000 =
6 670 km, to three significant figures.
360
360
22. Two towns are located on longitude 50 E. The towns are 5 200 km apart. Calculate the difference
in their latitudes.
Solution:
We are looking for in the formula d =
2R. d = 5200 km and 2R =
40 000, the
360
circumference of the Earth.
5 200 =
40 000
360
= 5 200 360 40 000
=
47
The two towns are 47 apart on longitude 50 E.
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
23. Find the length of the parallel of latitude 41 S.
+ !"#$%&'()*
Solution:
We know that r = R cos where r is the radius of the small
circle on latitude (N or S), and R is the radius of the Earth. So
r = R cos 41 .
The length of the small circle known as latitude 41 S is 2r =
2R cos 41 = 40 000 cos 41 =
30 200 km.
"
-.
"
#
-.
24. Two places are located on the parallel of latitude 32 N, one at longitude 47 W and the other at
longitude 25 E.
a) How far apart are the two towns, measured along the parallel of latitude 32 N?
b) If it takes a plane 10 hours to travel from one town to the other, calculate the speed of the
plane, correct to the nearest kilometer per hour.
Solution:
+ !"#$%&'()*
a) We know that r = R cos where r is the radius of the small circle
on latitude (N or S), and R is the radius of the Earth. So
r = R cos 32 .
"
-. +
-.
!
The angle between the places on latitude 32 N is 47 + 25 = 72 .
The distance between the two places is
,
72
72
72
2r =
2R cos 32 =
40 000 cos 32 =
6 780 km.
360
360
360
b) Using speed = distance time, speed = 6780 10 =
678 km/h.
The two places are 6 780 km apart and a plane travelling 678 km/h would
take about 10 hours to get there.
01 ./
"
!""
!#"
25. Two towns, P and Q, are located at (4 N, 100 E) and (4 N, 140 E),
respectively. Calculate the shortest distance from P to Q, along the
parallel of latitude 4 N.
Solution:
Both towns are located on latitude 4 N. The radius of latitude 4 N is r = R cos 4 where R is
the radius of the Earth.
The angle between the places on latitude 4 N is 140 100 = 40 .
The distance between the two places is
40
40
1
2R cos 4 = 40 000 cos 4 =
4 430 km.
2r =
360
360
9
WWW.C E M C .U WAT E R LO O.C A | T h e C E N T R E fo r E D U C AT I O N i n M AT H E M AT I C S a n d CO M P U T I N G
26. Havana and Canton are both on latitude 23 N, and their longitudes are
82.25 W and 113.25 E, respectively. Find their distance apart measured
along the parallel of latitude.
"
Solution:
%()#$
Both towns are located on latitude 23 N. The radius of latitude 23 N is r = R cos 23 where
%%&#"$ R
!"#"$
is the radius of the Earth.
!
%'$#$
The angle between the places on latitude 23 N is 82.25 + 113.25 = 195.5 . This angle is a reflex
angle so we can go the other way 360 195.5 = 164.5 and travel a shorter distance.
The distance between the two places is
164.5
164.5
164.5
2r =
2R cos 23 =
40 000 cos 23 =
16 800 km.
360
360
360
The distance from Havana to Canton along latitude 23 N is 16 800 km to three significant figures.
27. Cherepovets, Russia is located approximately at (60 N, 38 E) and Mt. Logan, Canada is located
approximately at (60 N, 142 W).
a) How far apart are the two locations, measured along the parallel of latitude 60 N?
b) Calculate the great circle distance between Cherepovets and Mt. Logan.
Solution:
a) Both Cherepovets and Mt. Logan are on latitude 60 N and they are 38 + 142 = 180
apart. This means that on latitude 60 N they are one half the circumference of this small
circle apart. We know that r = R cos 60 and hence the distance along the parallel of latitude 60 N is
1
2r = 0.5 2R cos 60 = 0.5 40 000 cos 60 = 10 000 km.
2
b) But since their longitudes are 180 apart, both Cherepovets and
Mt. Logan are located on a great circle through the North and
South Poles. The sector angle is 180 2 60 = 60 .
!"
!"
The great circle distance between Cherepovets and Mt. Logan is
60
1
2R = 40 000 =
6 670 km.
360
6
Therefore Cherepovets and Mt. Logan are 10 000 km apart along latitude 60 N and 6 670 km
apart along the great circle that passes through the North and South Poles.
You might also like
- Grade 10 Maths - Basic Paper 1 - Q - SDocument37 pagesGrade 10 Maths - Basic Paper 1 - Q - SPRAVEENA R.PNo ratings yet
- UntitledDocument13 pagesUntitledHazeel HashimNo ratings yet
- Lesson 3.0 Solutions of Right Triangles 3.1 Solving Right TrianglesDocument25 pagesLesson 3.0 Solutions of Right Triangles 3.1 Solving Right TrianglesJo HarNo ratings yet
- Geometry & Mensuration 3Document35 pagesGeometry & Mensuration 3Neetu Jain100% (2)
- Chapter 12Document174 pagesChapter 12Naurin FathimaNo ratings yet
- Class 10 Maths Term 2 Important QuestionsDocument13 pagesClass 10 Maths Term 2 Important QuestionsBhargavi JujjavarapuNo ratings yet
- C2 Trigonometry - QuestionsDocument17 pagesC2 Trigonometry - QuestionsRichard AdioNo ratings yet
- Prelims Math 2Document4 pagesPrelims Math 2Ramon Jr. MontesorNo ratings yet
- CAT Quant Questions PDFDocument65 pagesCAT Quant Questions PDFSuryansh SinghNo ratings yet
- CH5Document4 pagesCH5wenNo ratings yet
- Trigonometry: "Chance Favors Only The Prepared Only The Prepared Mind"Document75 pagesTrigonometry: "Chance Favors Only The Prepared Only The Prepared Mind"Ran Baltazar100% (3)
- 2 Week 1 Module 2 Math Practice Problems SolutionsDocument27 pages2 Week 1 Module 2 Math Practice Problems SolutionsDarren Ian MaalihanNo ratings yet
- The Boat Traveled 92.5 Feet.: Angle of ElevationDocument5 pagesThe Boat Traveled 92.5 Feet.: Angle of ElevationMNo ratings yet
- Note:: A B Q ODocument53 pagesNote:: A B Q OGiridharan RajanbabuNo ratings yet
- CAT Quant Questions PDFDocument63 pagesCAT Quant Questions PDFSHREYA MAHESHWARINo ratings yet
- Mathemathic SubjektifDocument10 pagesMathemathic Subjektifjoyce juok zhi shangNo ratings yet
- Some Geonmetry College ArchitecuteDocument7 pagesSome Geonmetry College ArchitecutepranavdeepakvNo ratings yet
- Pe 2 TrigonometryDocument10 pagesPe 2 TrigonometryJosuelle MadulaNo ratings yet
- NCERT Solutions For Class 10 Maths Chapter 9 Some Applications of TrigonometryDocument1 pageNCERT Solutions For Class 10 Maths Chapter 9 Some Applications of TrigonometryManroop SinghNo ratings yet
- Maharashtra-Mathematics Geometry Sample Paper-1-SOLUTION-Class 10 Question PaperDocument9 pagesMaharashtra-Mathematics Geometry Sample Paper-1-SOLUTION-Class 10 Question PaperFirdosh KhanNo ratings yet
- Higher Eng Maths 9th Ed 2021 Solutions ChapterDocument39 pagesHigher Eng Maths 9th Ed 2021 Solutions ChapterAubrey JosephNo ratings yet
- MATH 1720 Final Exam ReviewDocument12 pagesMATH 1720 Final Exam ReviewRafael Pati Liggayu IINo ratings yet
- 68 P SJV Ek CKndee VITIs 7Document15 pages68 P SJV Ek CKndee VITIs 7DEBJITA MAITY XI CNo ratings yet
- UKI M C: Solutions LeafletDocument4 pagesUKI M C: Solutions LeafletDoddy FeryantoNo ratings yet
- IGCSE TrigonometryDocument14 pagesIGCSE TrigonometryDienta Alias100% (10)
- 500 QuestionsDocument109 pages500 QuestionsRaghav Goyal 10 ENo ratings yet
- Trigro FinnDocument9 pagesTrigro Finnkenjam89mbNo ratings yet
- Geometry State Mathematics Finals Contest Solutions May 1, 2003Document9 pagesGeometry State Mathematics Finals Contest Solutions May 1, 2003biswajit karNo ratings yet
- TrigonometryDocument3 pagesTrigonometryShang Divina Ebrada50% (2)
- TestcdseDocument19 pagesTestcdsegurdeepchauhan_1No ratings yet
- Trigonometry TipqcDocument62 pagesTrigonometry TipqcMichael Damian50% (2)
- 2001 GeomsolDocument8 pages2001 Geomsolbiswajit karNo ratings yet
- Trigonometry 2Document5 pagesTrigonometry 2Laura ChandraNo ratings yet
- Chapter 15 GeometaryDocument7 pagesChapter 15 GeometaryDevyansh 9207No ratings yet
- Year 10 MathsDocument8 pagesYear 10 MathsEedris akinwandeNo ratings yet
- BLUEBOOK Compiler GEASDocument125 pagesBLUEBOOK Compiler GEASJusteinAlagenioNo ratings yet
- Chapter 10 - Angles of Elevation and DepressionDocument8 pagesChapter 10 - Angles of Elevation and DepressionNasir Rahman100% (1)
- 9th GeometryDocument28 pages9th Geometrywww.r2dk2No ratings yet
- Trigonometry ProblemsDocument19 pagesTrigonometry ProblemsLiezel-jheng Apostol Lozada100% (1)
- Chapter 15 I Trigonometry II ENHANCEDocument45 pagesChapter 15 I Trigonometry II ENHANCEjuriah binti ibrahim100% (1)
- Class 10 Chapter 10 Maths Important QuestionDocument13 pagesClass 10 Chapter 10 Maths Important Questionswarnimadas935No ratings yet
- NCERT Solution For CBSE Class 10 Maths Chapter 9 Some Applications of TrigonometryDocument15 pagesNCERT Solution For CBSE Class 10 Maths Chapter 9 Some Applications of TrigonometryJagdeep SinghNo ratings yet
- Maths (QB)Document5 pagesMaths (QB)Ashraf PathanNo ratings yet
- Circle - 1Document5 pagesCircle - 1parthdbz2005No ratings yet
- MathsDocument10 pagesMathsRaajeNo ratings yet
- Reviewer Advanced Physics PDFDocument54 pagesReviewer Advanced Physics PDFJocy Ross De Guzman0% (1)
- TrigandBearings ExercisesDocument2 pagesTrigandBearings ExercisesCoolman PoonNo ratings yet
- Math Review Let PDFDocument242 pagesMath Review Let PDFJener Parayno Fernandez100% (2)
- 07 GemoetryDocument11 pages07 GemoetryKomanduri Murali SrinivasNo ratings yet
- NCERT Solutions For CBSE Class 10 Maths Chapter 10 CirclesDocument15 pagesNCERT Solutions For CBSE Class 10 Maths Chapter 10 CirclesJayant KumarNo ratings yet
- A. Long ChordDocument10 pagesA. Long ChordHarvey PagaranNo ratings yet
- Solution MAT + SAT PDFDocument8 pagesSolution MAT + SAT PDFNinad AkolekarNo ratings yet
- Bec198 2 TrigonometryDocument4 pagesBec198 2 TrigonometryJohn Patrick DagleNo ratings yet
- NCERT Exemplar Class 9 MathsDocument47 pagesNCERT Exemplar Class 9 Mathsfunson123No ratings yet
- Circles Class 10th MCQ - 1Document15 pagesCircles Class 10th MCQ - 1Melissa CouthinoNo ratings yet
- Math Foundation Review Teacher's Edition: TrigonometryDocument24 pagesMath Foundation Review Teacher's Edition: TrigonometrytwsttwstNo ratings yet
- Trigonometric RatiosDocument14 pagesTrigonometric RatiosGIDEON PAULNo ratings yet
- ATI TEAS Calculation Workbook: 300 Questions to Prepare for the TEAS (2023 Edition)From EverandATI TEAS Calculation Workbook: 300 Questions to Prepare for the TEAS (2023 Edition)No ratings yet
- 12.215 Homework #1 SolutionsDocument6 pages12.215 Homework #1 SolutionsHeaven 156No ratings yet
- Compass Rule and Transit RuleDocument14 pagesCompass Rule and Transit RuleJeffrey SumambotNo ratings yet
- Applications of The Residue Theorem To Real Integrals-Supplementary Material by Pawel HitczenkoDocument14 pagesApplications of The Residue Theorem To Real Integrals-Supplementary Material by Pawel Hitczenkohyd arnes100% (1)
- Inverse Trigonometric FunctionsDocument23 pagesInverse Trigonometric FunctionsSudeepNo ratings yet
- Trig Sec 8Document4 pagesTrig Sec 8JSPAMoreNo ratings yet
- Cbse Class Xi Physics Ch2Document10 pagesCbse Class Xi Physics Ch2sujayan2005No ratings yet
- Rs3883 - Optinal Maths Grade 10 English VersionDocument293 pagesRs3883 - Optinal Maths Grade 10 English VersionPrashim Raj Shrestha100% (1)
- Swedge: Verification ManualDocument58 pagesSwedge: Verification ManualWahyu Nusantara AkbarNo ratings yet
- Ecet CP 11 Stu PDFDocument7 pagesEcet CP 11 Stu PDFChai Usajai UsajaiNo ratings yet
- L2 - Trigonometric Ratios in Right TriangleDocument5 pagesL2 - Trigonometric Ratios in Right TriangleKienNo ratings yet
- Inmo-2012 Previous Year Question Papers of Indian National Mathematical Olympiad (INMO) With SolutionsDocument6 pagesInmo-2012 Previous Year Question Papers of Indian National Mathematical Olympiad (INMO) With SolutionsAkshay PandeyNo ratings yet
- Calculus II by Paul DawkinsDocument379 pagesCalculus II by Paul Dawkinsdandalf02100% (1)
- AQA Core 3 Revision BookletDocument20 pagesAQA Core 3 Revision Bookletjake1731No ratings yet
- Differentiation Under The Integral SignDocument23 pagesDifferentiation Under The Integral SignAlex HiticașNo ratings yet
- Graph of Cosecant and Secant Function BY: Group 2Document13 pagesGraph of Cosecant and Secant Function BY: Group 2Lucelyn Lugas CapoyNo ratings yet
- %% PART 1 % N Input ('Desired Number of Plot Points ')Document15 pages%% PART 1 % N Input ('Desired Number of Plot Points ')yelyah seriousNo ratings yet
- Paan Trigono BoarderDocument2 pagesPaan Trigono BoarderRozieana IshakNo ratings yet
- DAX Cheat SheetDocument12 pagesDAX Cheat SheetRaviNo ratings yet
- 4-10 HWDocument4 pages4-10 HWli fNo ratings yet
- Trigonometry FormulasDocument2 pagesTrigonometry Formulasedgarsubs100% (3)
- Rotating ShipDocument7 pagesRotating ShipMark Eichenlaub100% (1)
- SAT II Physics Formula SheetDocument10 pagesSAT II Physics Formula Sheetalex100% (1)
- Iteration Question'sDocument17 pagesIteration Question'sAyra MujibNo ratings yet
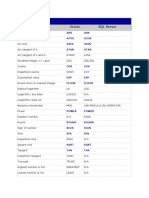
- Math Functions: Function Oracle SQL ServerDocument3 pagesMath Functions: Function Oracle SQL ServerSivaprasad ReddyNo ratings yet
- Trigonometry Plane&Solid Geometry: By: Engr. Roy Andrew GarciaDocument50 pagesTrigonometry Plane&Solid Geometry: By: Engr. Roy Andrew GarciaEraAlmen100% (1)
- Workbook - Trigonometric Equations by MC SirDocument17 pagesWorkbook - Trigonometric Equations by MC SirRahul KumarNo ratings yet
- Calculus 1 FormulaDocument2 pagesCalculus 1 FormulaAuto CadNo ratings yet
- Lift Line TheoryDocument19 pagesLift Line TheoryMuzakkir Sharieff100% (1)
- Offtracking: VehicleDocument10 pagesOfftracking: VehicleGeraldo Gil CorreiaNo ratings yet