N5625

Communication
Systems I
ECE 5625/4625 Lecture Notes
Spring 2007
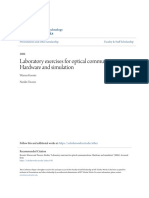
Input
Message
Message
Signal
Input
Transducer
Output
Message
Transmitted
Signal
Transmitter
Noise and distortion

enters the system
here
Channel
Output
Signal
Output
Transducer
2007
Mark A. Wickert
Received
Signal
Receiver
Chapter
Course Introduction/Overview
Contents
1.1
Introduction . . . . . . . . . . . . . . . . . . . . . . .
1-3
1.2
Where are we in the Curriculum? . . . . . . . . . . .
1-4
1.3
Where are we (cont)? . . . . . . . . . . . . . . . . . .
1-5
1.4
Course Syllabus . . . . . . . . . . . . . . . . . . . . .
1-6
1.5
Instructor Policies . . . . . . . . . . . . . . . . . . . .
1-7
1.6
Communication Lab Connection . . . . . . . . . . . .
1-8
1.7
Software Tools . . . . . . . . . . . . . . . . . . . . . .
1-9
1.8
Comm I/Comm II Course Sequence . . . . . . . . . . 1-10
1.9
Course Introduction and Overview . . . . . . . . . . . 1-11
1.10 A Block Diagram . . . . . . . . . . . . . . . . . . . . . 1-12

1.11 Channel Types . . . . . . . . . . . . . . . . . . . . . . 1-13
1.11.1 Electromagnetic-wave (EM-wave) propagation . 1-13
1.11.2 Guided EM-wave propagation . . . . . . . . . . 1-17
1.11.3 Magnetic recording channel . . . . . . . . . . . 1-17
1.11.4 Optical channel . . . . . . . . . . . . . . . . . . 1-17
1-1
CHAPTER 1. COURSE INTRODUCTION/OVERVIEW
1-2
ECE 5625 Communication Systems I
1.1. INTRODUCTION
1.1
Introduction
Where are we in the ugrad and grad curriculum?

Course Syllabus
Instructor policies
Relationship to the communications lab, ECE 4670
Software tools
The Comm I/Comm II course sequence
Communication systems overview
1-3
1-4
Calculus II
Calculus III
Diff. Eq.
Physics II
Physics III
Physical
Electronics
Emag. II
Microwave
Meas. Lab
Senior
Design
EM Theory
& Apps.
Senior
Seminar
Calculus I
CMOS RF
IC Design
Emag. I
Prob. &
Statistics
uComputer
System Lab
Signals &
Systems
Semocond.
Devices II
VLSI Fab
Lab
Mixed Sig.
IC Design
VLSI Circ
Design
Analog IC
Design
Electron. II
& Lab
Circuits &
Systems II
Semicond.
Devices I
Logic
Circuits II
Computer
Modeling
Circuits &
Systems I
Logic
Circuits I
Intro. to
Robotics
VLSI
Processing
ADD Lab
Electron. I
& Lab
Embedded
Sys Design
uCmp Sys
& uP Lab
Rapid Prototype, FPGA
Advanced
Dig. Des.
Computer
Arch Design
Technical
Writing
Rhetoric &
Writing I
Multivar
Control I
Feedback
Ctrl & Lab
Signal
Process Lab
Electron. I
Lab
Circuits &
Systems II
Prob. &
Statistics
Communic
Lab
Electron. I
Lab
Real Time
DSP
Modern
DSP
Prob. &
Statistics
Communic
Systems II
Communic
Systems I
Circuits &
Systems II
1.2
Physics I
Where are we in the Curriculum?
1.3. WHERE ARE WE (CONT)?
1.3
Where are we (cont)?

ECE 2610
Signals &
Systems
ECE 2205
Signals &
Systems I
ECE 3205
Signals &
Systems II
ECE 3610
Eng. Prob.
& Stats.
ECE 5650
Modern
DSP
ECE 4680
DSP
Lab
ECE 5625
Comm.
Systems I
ECE 4670
Comm.
Lab
You are Here!
ECE 5655
Real-Time
DSP
ECE 5615
Statistical
Signal Proc
ECE 5630
Comm.
Systems II
ECE 5610
Random
Signals
ECE 5675
PLL &
Applic.
ECE 6640
Spread
Spectrum
ECE 6620
Detect. &
Estim. Thy.
ECE 5720
Optical
Comm.
ECE 5635
Wireless
Comm.
ECE 6650
Estim. &
Adapt. Fil.
Coding Thy,
Image Proc,
Sat. Comm,
Radar Sys
Courses Offered According to Demand
1-5
!! ! ! !1.4
! ! !!! !!! ! !
Course Syllabus
"#"!$%&$'(%&$
#)**+,-./,)+!012/3*2!4
"#$%&'!"()(*+($!,--.
Instructor:
/$0!12$3!4%53($+
Office:!67,,8
<%53($+=(2*0>55*0(?>
B++#CDD(2*0>55*0(?>D<%53($+D(5(;8,;D
Phone:!,8,9:;-Fax:!,8,9:;@A
Office Hrs:
4(?&(*?2E!FFC--!G1HF,C--!I1J!*>''(*+!2!+%)(J!K+B($!+%)(*!LE!2##K%&+)(&+!!
Required
Texts:
M0!N%()($!2&?!40!O$2&+($J! "#$%&$'()*!+,!-+../%$&01$+%*J!!P+B!(?%+%K&J!I$(&9
+%5(!Q2RRJ!,--S0
Optional
Software:
1GOTGU! "+>?(&+!V($*%K&! <%+B! "%)>R%&3! <%+B! 1GOTGU! .0WJ! "%)>R%&3! ;0WJ

2&?!"E)LKR%5!12+B!OKKRLKW!X&K!)2+$%W!*%Y(!R%)%+*Z0!G&!%&+($25+%[(!&>)($%52R
2&2RE*%*J! ?2+2! 2&2RE*%*J! 2&?! '$2#B%5*! #2532'(! PK$! 4%&?K<*DT%&>WD125! \"]
^AA0A;0!OB(! "%'&2R! I$K5(**%&'! +KKRLKW! )2E! L(! >*(P>R! 2+! ^,A0A;0! \$?($! P$K)
"""#$%&'"()*+#,($-+&./01&0!7K+(C!OB(!6_6!I_!T2L!B2*!+B(!P>RR![($9
*%K&!KP!1GOTGU!2&?!"%)>R%&3!PK$!<%&?K<*!X[($0!.0WZ!<%+B!)2&E!+KKRLKW(*0
Grading:
F0Z
,0Z
:0Z
S0Z
`$2?(?!BK)(<K$3!2**%'&)(&+*!2&?DK$!*BK$+!a>%YY(*!+K+2R!,-b0
_K)#>+($!#$Kc(5+X*Z!<K$+B!,-b
O<K!dQK>$e!(W2)*!2+!F;b!(25BJ!:-b!+K+2R0
f%&2R!(W2)!<K$+B!:-b0
Topics
Text Sections
F0! g&+$K?>5+%K&!2&?!_K>$*(!\[($[%(<
7K+(*
,0! "%'&2R!2&?!R%&(2$!*E*+()!$([%(<!2&?!%&+$K?>5+%K&!+K!&(<!+K#9
%5*!%&5R>?%&'!'(&($2R%Y(?!fK>$%($!*($%(*J!2>+K5K$$(R2+%K&!P>&59
+%K&J!#K<($!*#(5+$>)J!Q%RL($+!+$2&*PK$)!2&?!*2)#R%&'!+B(K$E
:0! G&2RK'!)K?>R2+%K&!+(5B&%a>(*J!/"UJ!G1J!""UJ!V"UJ!f1J!
I1J!2&?!#>%R*(!)K?>R2+%K&
_B2#+($!:
S0! \[($[%(<!KP!?%'%+2R!)K?>R2+%K&!+(5B&%a>(*
7K+(*!2&?!!
_B2#+($!S
;0! 7K%*(!*K>$5(*!2&?!52R5>R2+%K&*!
1-6
,0FH,0@J!,0F-
G##(&?%W!G
1.5. INSTRUCTOR POLICIES
1.5
Instructor Policies
Homework papers are due at the start of class

If business travel or similar activities prevent you from attending class and turning in your homework, please inform me beforehand
Grading is done on a straight 90, 80, 70, ... scale with curving
below these thresholds if needed
Homework solutions will be placed on the course Web site in
PDF format with security password required; hints pages may
also be provided
1-7
1.6
Communication Lab Connection
The labs are fairly tightly coupled with the lecture topics
The communications hardware experience should enhance your
understanding of communications theory and analysis
Lab topics:
Linear System Characteristics
Spectrum Analysis
DSB and AM Modulation and Demodulation
AM Superheterodyne Receivers
Frequency Modulation and Demodulation
Second Order Phase-Lock Loops
Communications building blocks are dealt with for the most
part as electronic subsystems
The spectrum analyzer and vector network analyzer are introduced to extend measurement capabilities into the frequency
domain
1-8
1.7. SOFTWARE TOOLS
1.7
Software Tools
Analysis aids
Calculator, MATLAB, Mathematica, others
System simulation
MATLAB/Simulink, VisSim/Comm (used in ECE 4670),
others
Circuit simulation
Spice type simulator, e.g. the free simulator Qucs available at http://qucs.sourceforge.net/
1-9
1.8
Comm I/Comm II Course Sequence
Communication systems I, this course, continues into a second semester when ECE 4630/5630 is offered alternate fall
semesters
The second semester course focuses on digital communications
An introduction to random signals is provided
Amplitude, Phase, and frequency shift-keyed modulation
schemes are studied in considerable detail
Coherent versus non-coherent modulation
The Mobile radio channel is introduced
Satellite communications is introduced
Coding theory is introduced
1-10
1.9. COURSE INTRODUCTION AND OVERVIEW
1.9
Course Introduction and Overview
The theory of systems for the conveyance of information

Communication systems must deal with uncertainty (noise and
interference)
The uncertainty aspects of noise require the use of probability, random variables, and random processes
In this first course deterministic modeling is used for the
most part
Some important dates:
1915
1918
1938
WW II
1948
1956
1960
1962
1970s
1977
1980
1990s
1990s
1998
Transcontinental telephone line completed

Armstrong superheterodyne radio receiver perfected
Television broadcasting begins
Radar and microwave systems developed
Transistor invented
First transoceanic telephone line completed
Laser demonstrated
First communications satellite, Telstar I
Commercial relay satellites for voice and data
Fiber optic communication systems
Satellite switchboards in the sky
Global positioning system (GPS) completed
Cellular telephones widely used
Global satellite-based cellular telephone system
1-11
1.10
A Block Diagram
A a high level communication systems are typically described

using a block diagram
Input
Message
Message
Signal
Input
Transducer
Output
Message
Transmitted
Signal
Transmitter
Noise and distortion

enters the system
here
Channel
Received
Signal
Output
Signal
Output
Transducer
Receiver
There is an information source as the input and an information

sink to receive the output
The block diagram shown above is very general
The source may be digital or analog
The transmission may be at baseband or on a radio frequency (RF) carrier
The channel can take on may possible forms
1-12
1.11. CHANNEL TYPES
1.11
Channel Types
1.11.1
Electromagnetic-wave (EM-wave) propagation

Comm Satellite
Transiosphere (LOS)
Ionosphere
Line-of-sight
propagation
Skip-wave
propagation
Ground wave
propagation
Earth
When you think wireless communications this is the channel

type most utilized
The electromagnetic spectrum is a natural resource
The above figure depicts several propagation modes
Lower frequencies/long wavelengths tend to follow the
earths surface
Higher frequencies/short wavelengths tend to propagate
in straight lines
Reflection of radio waves by the ionosphere occurs for frequencies below about 100 MHz (more so at night)
1-13
1-14
1.11. CHANNEL TYPES
Examples of public (commercial) and government (military

applications and the frequency bands they operate in
There is a hierarchy of organizations that regulate how the

available spectrum is allocated
Worldwide there is the International Telecommunications
Union (ITU), which convenes regional and worldwide Administrative Radio Conferences (RARC & WARC)
Within the United States we have the Federal Communications Commission (FCC)
Cellular telephony, wireless LAN (WLAN), and HDTV broadcasting, are examples where the FCC continues to make allocation changes
1-15
At frequencies above 12 GHz oxygen and water vapor absorb

and scatter radio waves
Satellite communications, which use the microwave frequency
bands, must account for this in what is known as the link power
budget
Water vapor
and oxygen
attenuation
23
62
120
Rainfall rate
attenuation
1-16
1.11. CHANNEL TYPES
1.11.2
Guided EM-wave propagation
Communication using transmission lines such as twisted-pair

and coax cable
1.11.3
Magnetic recording channel
Disk drives, fixed (at one time flexible too)

Video and audio
1.11.4
Optical channel
Free-space
Fiber-optic
CD, DVD, HD-DVD, etc.
1-17
Example 1.1: Distortion in a Sat-Comm Channel

Wideband satellite communication channels are subject to both
linear and non-linear distortion
Transmitter
PSK
Mod
Modulation
Impairments
Bandpass
Filtering
HPA
(TWTA)
! BPSK
! IQ amplitude imbalance ! Spurious PM
! QPSK ! IQ phase imbalance
! Incidental AM
! OQPSK ! Waveform asymmetry
! Clock jitter
and rise/fall time
!
!
!
!
Phase noise
Spurious PM
Incidental AM
Spurious outputs
Other
Signals
Downlink
Channel
Mod.
HPA
(TWTA)
WGN
Noise
(off)
Other
Signals
Transponder
Bandpass
Filtering
Mod.
Data
Source
Uplink
Channel
WGN
Noise
(on)
Bandpass
Filtering
Mod.
Receiver
PSK Demod
(bit true with
full synch)
Adaptive
Equalizer
Recovered
Data
! Phase noise
Other ! Spurious PM
Signals ! Incidental AM
! Spurious outputs
Wideband Sat-Comm simulation model
An adaptive filter can be used to estimate the channel distortion, for example a technique known as decision feedback
equalization
1-18
1.11. CHANNEL TYPES
Decision
Feedback
+
M1 Tap
Complex Re
FIR
Soft I/Q outputs

from demod at
sample rate = 2Rs
M1 Tap
Complex Im
FIR
M2 Tap
Real
FIR
Recovered
I Data
2
Adapt
Tap
CM Error/ Mode
DD Error/
Weight LMS Update
LMS Update
Update
CM, DD CM Error/
DF,
LMS Update
z-1
Stagger for
OQPSK, omit
for QPSK
DD Error/
LMS Update
+
-
+
Recovered
Q Data
Decision
Feedback
M2 Tap
Real
FIR
An adaptive baseband equalizer implemented in FPGA1
Since the distortion is both linear (bandlimiting) and nonlinear (amplifiers and other interference), the distortion cannot be
completely eliminated
The following two figures show first the modulation 4-phase
signal points with and with out the equalizer, and then the bit
error probability (BEP) versus received energy per bit to noise
power spectral density ratio (E b /N0)
1 Mark Wickert,
Shaheen Samad, and Bryan Butler. An Adaptive Baseband Equalizer for High
Data Rate Bandlimited Channels, Proceedings 2006 International Telemetry Conference, Session
5, paper 065-03.
1-19
1.5
Before Equalization: Rb = 300 Mbps
1.5
0.5
0.5
Quadrature
Quadrature
0.5
0.5
1.5
1.5
0.5
0
0.5
Inphase
After Equalization: Rb = 300 Mbps
1.5
1.5
1.5
0.5
0
0.5
Inphase
1.5
OQPSK scatter plots with and without the equalizer

2
10
300 MBPS BER Performance with a 40/0 Equalizer

Semi-Analytic Simulation
Probability of Bit Error
10
10
10
Theory
EQ
NO EQ
10
10
4.0 dB
10
12
14
16
Eb/N0 (dB)
8.1 dB
18
20
22
24
BEP versus E b /N0 in dB
1-20
Chapter
Signal and Linear System Analysis

Contents
2.1
Signal Models . . . . . . . . . . . . . . . . . . . . . .
2-3
2.1.1
Deterministic and Random Signals . . . . . . . .
2-3
2.1.2
Periodic and Aperiodic Signals . . . . . . . . . .
2-3
2.1.3
Phasor Signals and Spectra . . . . . . . . . . . .
2-4
2.1.4
Singularity Functions . . . . . . . . . . . . . . .
2-7
2.2
Signal Classifications . . . . . . . . . . . . . . . . . . 2-11
2.3
Generalized Fourier Series . . . . . . . . . . . . . . . 2-14
2.4
Fourier Series . . . . . . . . . . . . . . . . . . . . . . 2-20
2.5
2.4.1
Complex Exponential Fourier Series . . . . . . . 2-20
2.4.2
Symmetry Properties of the Fourier Coefficients
2.4.3
Trigonometric Form . . . . . . . . . . . . . . . 2-25
2.4.4
Parsevals Theorem . . . . . . . . . . . . . . . . 2-26
2.4.5
Line Spectra . . . . . . . . . . . . . . . . . . . 2-26
2.4.6
Numerical Calculation of X n . . . . . . . . . . . 2-31
2.4.7
Other Fourier Series Properties . . . . . . . . . . 2-37
2-23
Fourier Transform . . . . . . . . . . . . . . . . . . . . 2-38

2.5.1
Amplitude and Phase Spectra . . . . . . . . . . 2-39
2-1
CHAPTER 2. SIGNAL AND LINEAR SYSTEM ANALYSIS
2.6
2.7
2.5.2
Symmetry Properties . . . . . . . . . . . . . . . 2-39
2.5.3
Energy Spectral Density . . . . . . . . . . . . . 2-40
2.5.4
Transform Theorems . . . . . . . . . . . . . . . 2-42
2.5.5
Fourier Transforms in the Limit . . . . . . . . . 2-51
2.5.6
Fourier Transforms of Periodic Signals . . . . . 2-53
2.5.7
Poisson Sum Formula . . . . . . . . . . . . . . 2-59
Power Spectral Density and Correlation . . . . . . . . 2-60

2.6.1
The Time Average Autocorrelation Function . . 2-61
2.6.2
Power Signal Case . . . . . . . . . . . . . . . . 2-62
2.6.3
Properties of R( ) . . . . . . . . . . . . . . . . 2-63
Linear Time Invariant (LTI) Systems . . . . . . . . . 2-70

2.7.1
Stability . . . . . . . . . . . . . . . . . . . . . . 2-72
2.7.2
Transfer Function . . . . . . . . . . . . . . . . . 2-72
2.7.3
Causality . . . . . . . . . . . . . . . . . . . . . 2-73
2.7.4
Properties of H ( f ) . . . . . . . . . . . . . . . . 2-74
2.7.5
Response to Periodic Inputs . . . . . . . . . . . 2-78
2.7.6
Distortionless Transmission . . . . . . . . . . . 2-78
2.7.7
Group and Phase Delay . . . . . . . . . . . . . . 2-79
2.7.8
Nonlinear Distortion . . . . . . . . . . . . . . . 2-83
2.7.9
Ideal Filters . . . . . . . . . . . . . . . . . . . . 2-85
2.7.10 Realizable Filters . . . . . . . . . . . . . . . . . 2-87

2.7.11 Pulse Resolution, Risetime, and Bandwidth . . . 2-91
2.8
Sampling Theory . . . . . . . . . . . . . . . . . . . . . 2-97
2.9
The Hilbert Transform . . . . . . . . . . . . . . . . . 2-97
2.10 The Discrete Fourier Transform and FFT . . . . . . . 2-97
2-2
2.1. SIGNAL MODELS
2.1
Signal Models
2.1.1
Deterministic and Random Signals
Deterministic Signals, used for this course, can be modeled as

completely specified functions of time, e.g.,
x(t) = A(t) cos[2 f 0(t)t + (t)]
Note that here we have also made the amplitude, frequency, and phase functions of time
To be deterministic each of these functions must be completely specified functions of time
Random Signals, used extensively in Comm Systems II, take
on random values with known probability characteristics, e.g.,
x(t) = x(t, i )
where i corresponds to an elementary outcome from a sample
space in probability theory
The i create a ensemble of sample functions x(t, i ), depending upon the outcome drawn from the sample space
2.1.2
Periodic and Aperiodic Signals
A deterministic signal is periodic if we can write

x(t + nT0) = x(t)
for any integer n, with T0 being the signal fundamental period
2-3
A signal is aperiodic otherwise, e.g.,
1, |t| 1/2
(t) =
0, otherwise
(a) periodic signal, (b) aperiodic signal, (c) random signal
2.1.3
Phasor Signals and Spectra
A complex sinusoid can be viewed as a rotating phasor

x(t)
= Ae j (0t+),
< t <
This signal has three parameters, amplitude A, frequency 0,

and phase
The fixed phasor portion is Ae j while the rotating portion is
e j0t
2-4
2.1. SIGNAL MODELS
This signal is periodic with period T0 = 2/0

It also related to the real sinusoid signal A cos(0t + ) via
Eulers theorem
x(t) = Re x(t)
= Re A cos(0t + ) + j A sin(0t + )
= A cos(0t + )
(a) obtain x(t) from x(t),
(b) obtain x(t) from x(t)

and x (t)
We can also turn this around using the inverse Euler formula
x(t) = A cos(0t + )
1
1
= x(t)
+ x (t)
2
2
j (0 t+)
Ae
+ Ae j (0t+)
=
2
The frequency spectra of a real sinusoid is the line spectra plotted in terms of the amplitude and phase versus frequency
2-5
The relevant parameters are A and for a particular f 0 =

0/(2)
(a) Single-sided line spectra, (b) Double-sided line spectra
Both the single-sided and double-sided line spectra, shown

above, correspond to the real signal x(t) = A cos(2 f 0t + )
Example 2.1: Multiple Sinusoids

Suppose that
x(t) = 4 cos(2(10)t + /3) + 24 sin(2(100)t /8)
Find the two-sided amplitude and phase line spectra of x(t)

First recall that cos(0t /2) = sin(0t), so
x(t) = 4 cos(2(10)t + /3) + 24 cos(2(100)t 5/8)
The complex sinusoid form is directly related to the two-sided

line spectra since each real sinusoid is composed of positive
and negative frequency complex sinusoids
j (2(10)t+/3)
j (2(10)t+/3)
x(t) = 2 e
+e
j (2(100)t5/8)
j (2(100)t5/8)
+ 12 e
+e
2-6
2.1. SIGNAL MODELS
Amplitude
12
2
-100
-10
5/8
100
10
Phase
/3
-/3
f (Hz)
f (Hz)
-5/8
Two-sided amplitude and phase line spectra
2.1.4
Singularity Functions
Unit Impulse (Delta) Function

Singularity functions, such as the delta function and unit step
The unit impulse function, (t) has the operational properties
t2
(t t0) dt = 1, t1 < t0 < t2
t1
(t t0) = 0, t = t0
which implies that for x(t) continuous at t = t0, the sifting

property holds

x(t)(t t0) dt = x(t0)
Alternatively the unit impulse can be defined as

x(t)(t) dt = x(0)
2-7
Properties:
1. (at) = (t)/|a|
2. (t) = (t)
3. Sifting property special cases
t2
x(t0),
x(t)(t t0) dt = 0,
t1
undefined,
4. Sampling property
t1 < t0 < t2
otherwise
t0 = t1 or t0 = t2
x(t)(t t0) = x(t0)(t t0)
for x(t) continuous at t = t0
5. Derivative property
t2
x(t) (n)(t t0) dt = (1)n x (n)(t0)
t1
d
x(t)
n
= (1)
n
dt t=t0
Note: Dealing with the derivative of a delta function requires care
A test function for the unit impulse function helps our intuition
and also helps in problem solving
Two functions of interest are
1
,
1
t
(t) =
= 2
2
2
0,
1
t 2
1 (t) =
sin
t
2-8
|t|
otherwise
2.1. SIGNAL MODELS
Test functions for the unit impulse (t): (a) (t), (b) 1 (t)
In both of the above test functions letting 0 results in a

function having the properties of a true delta function
Unit Step Function
The unit step function can be defined in terms of the unit impulse
t <0
t
0,
u(t)
( ) d = 1,
t >0
undefined, t = 0
also
(t) =
du(t)
dt
2-9
Example 2.2: Unit Impulse 1st-Derivative

Consider
x(t) (t) dt
Using the rectangular pulse test function, (t), we note that

1
t also 1
(t) =
=
u(t + ) u(t )
2
2
2
and
d (t)
1
=
(t + ) (t )
dt
2
Placing the above in the integrand with x(t) we obtain, with

the aid of the sifting property, that

1
x(t) (t) dt = lim
x(t + ) x(t )
0 2
x(t ) x(t + )
= lim
0
2
= x (0)
2-10
2.2. SIGNAL CLASSIFICATIONS
2.2
Signal Classifications
From circuits and systems we know that a real voltage or current waveform, e(t) or i(t) respectively, measured with respective a real resistance R, the instantaneous power is
P(t) = e(t)i(t) = i 2(t)R W
On a per-ohm basis, we obtain
p(t) = P(t)/R = i 2(t) W/ohm
The average energy and power can be obtain by integrating
over the interval |t| T with T
T
E = lim
i 2(t) dt Joules/ohm
T T
T
1
P = lim
i 2(t) dt W/ohm
T 2T T
In system engineering we take the above energy and power
definitions, and extend them to an arbitrary signal x(t), possibly complex, and define the normalized energy (e.g. 1 ohm
system) as
E = lim
|x(t)| dt =
T T
T
1
P = lim
|x(t)|2 dt
T 2T T
|x(t)|2 dt
2-11
Signal Classes:
1. x(t) is an energy signal if and only if 0 < E < so that
P=0
2. x(t) is a power signal if and only if 0 < P < which

implies that E
Example 2.3: Real Exponential

Consider x(t) = Aet u(t) where is real
For > 0 the energy is given by

t 2
A2e2t
E=
Ae
dt =
2 0
0
A2
=
2
For = 0 we just have x(t) = Au(t) and E
For < 0 we also have E
In summary, we conclude that x(t) is an energy signal for >
0
For > 0 the power is given by
1 A2
T
P = lim
1e
=0
T 2T 2
For = 0 we have
1
A2
2
P = lim
A T =
T 2T
2
2-12
2.2. SIGNAL CLASSIFICATIONS
For < 0 we have P

In summary, we conclude that x(t) is a power signal for = 0
Example 2.4: Real Sinusoid

Consider x(t) = A cos(0t + ), < t <
The signal energy is infinite since upon squaring, and integrating over one cycle, T0 = 2/0, we obtain
N T0/2
E = lim
A2 cos2(0t + ) dt
N N T /2
T0 0/2
= lim N
A2 cos2(0t + ) dt
N
T0 /2
A2 T0/2
= lim N
1 + cos(20t + 2 ) dt
N
2 T0/2
A2
= lim N
T0
N
2
The signal average power is finite since the above integral is
normalized by 1/(N T0), i.e.,
1
A2
A2
P = lim
N
T0 =
N N T0
2
2
2-13
2.3
Generalized Fourier Series
The goal of generalized Fourier series is to obtain a representation of

a signal in terms of points in a signal space or abstract vector space.
The coordinate vectors in this case are orthonomal functions. The
complex exponential Fourier series is a special case.
Let A be a vector in a three dimensional vector space
Let a1, a2, and a3 be linearly independent vectors in the same
three dimensional space, then
c1a1 + c2a2 + c3a3 = 0 (zero vector)
only if the constants c1 = c2 = c3 = 0
The vectors a1, a2, and a3 also span the three dimensional space,
that is for any vector A there exists a set of constants c1, c2, and
c3 such that
A = c1a1 + c2a2 + c3a3
The set {
a1, a2, a3} forms a basis for the three dimensional
space
Now let {
a1, a2, a3} form an orthogonal basis, which implies
that
ai a j = (
ai , a j ) =
ai , a j = 0, i = j
which says the basis vectors are mutually orthogonal
From analytic geometry (and linear algebra), we know that we

can find a representation for A as
(
a1 A)
(
a2 A)
(
a3 A)
A =
+
+
|
a 1 |2
|
a2|2
|
a3|2
2-14
2.3. GENERALIZED FOURIER SERIES
which implies that

A =
where
i=1
ci ai
ai A
ci =
, i = 1, 2, 3
|
ai |2
is the component of A in the ai direction
We now extend the above concepts to a set of orthogonal functions {1(t), 2(t), . . . , N (t)} defined on to t t0 + T ,
where the dot product (inner product) associated with the n s
is
t0+T
m (t), n (t) =
m (t)n(t) dt
t0
cn , n = m
= cn mn =
0, n = m
The n s are thus orthogonal on the interval [t0, t0 + T ]
Moving forward, let x(t) be an arbitrary function on [t0, t0 +T ],
and consider approximating x(t) with a linear combination of
n s, i.e.,
x(t) xa (t) =
n=1
X n n (t), t0 t t0 + T,
where a denotes approximation

2-15
A measure of the approximation error is the integral squared

error (ISE) defined as
N =
x(t) xa (t) dt,
where
denotes integration over any T long interval
To find the X n s giving the minimum N we expand the above

integral into three parts (see homework problems)
2
N
1
2
N =
|x(t)| dt
x(t)n (t) dt
c
T
T
n=1 n
+
cn X n
x(t)n (t) dt
cn T
n=1
Note that the first two terms are independent of the X n s

and the last term is nonnegative (missing steps are in text
homework problem 2.14)
We conclude that N is minimized for each n if each element
of the last term is made zero by setting
1
Xn =
x(t)n(t) dt Fourier Coefficient
cn T
This also results in
2-16
min
|x(t)|2 dt
n=1
cn |X n |2
Definition: The set of of n s is complete if

lim ( N )min = 0
for
N
T
|x(t)|2 dt <
Even if though the ISE is zero when using a complete

set of orthonormal functions, there may be isolated points
where x(t) xa (t) = 0
Summary
x(t) = l.i.m.
Xn =
1
cn
X n n (t)
n=1
x(t)n(t) dt
The notation l.i.m. stands for limit in the mean, which is

a mathematical term referring to the fact that ISE is the
convergence criteria
Parsevals theorem: A consequence of completeness is
|x(t)|2 dt =
cn |X n |2
T
n=1
2-17
Example 2.5: A Three Term Expansion

Approximate the signal x(t) = cos 2 t on the interval [0, 1]
using the following basis functions
x(t)
0.75
0.75
0.5
0.5
0.25
0.25
0.2
0.4
0.6
0.8
-0.25
-0.25
-0.5
-0.5
-0.75
-0.75
-1
-1
2(t)
0.2
0.4
0.6
0.8
0.2
0.4
0.6
0.8
3(t)
1
0.75
0.75
0.5
0.5
0.25
0.25
0.2
1(t)
0.4
0.6
0.8
-0.25
-0.25
-0.5
-0.5
-0.75
-0.75
-1
-1
Signal x(t) and basis functions i (t), i = 1, 2, 3
To begin with it should be clear that 1(t), 2(t), and 3(t)

are mutually orthogonal since the integrand associated with the
inner product, i (t) j (t) = 0, for i = j, i, j = 1, 2, 3
2-18
Before finding the X n s we need to find the cn s
1/4
c1 =
|1(t)|2 dt
|1|2 dt = 1/4
0
T
c2 =
|2(t)|2 dt = 1/2
T
c3 =
|3(t)|2 dt = 1/4
T
Now we can compute the X n s:
X 1 = 4 x(t)1(t) dt
T 1/4
1/4
2
2
=4
cos(2 t) dt = sin(2 t) =
0
0 3/4
3/4 2
1
X2 = 2
1/4
1/4
1
1
2
2
X3 = 4
3/4
3/4
1
x(t)
0.75
2/
xa(t)
0.5
0.25
0.2
0.4
0.6
0.8
-0.25
-0.5
-2/
-0.75
-1
Functional approximation
2-19
The integral-squared error, N , can be computed as follows:

2

3
x(t)
dt
N =
X
(t)
n n
n=1
|x(t)|2 dt
n=1
cn |X n |2
2
2
2
1 1 2
1 2
1 2
=
2 4
2
4
2
1 2
= = 0.0947
2
2.4
Fourier Series
When we choose a particular set of basis functions we arrive at the

more familiar Fourier series.
2.4.1
Complex Exponential Fourier Series
A set of n s that is complete is

n (t) = e jn0t , n = 0, 1, 2, . . .
over the interval (t0, t0 + T0) where 0 = 2/T0 is the period
of the expansion interval
2-20
2.4. FOURIER SERIES
proof of orthogonality
t0+T0
t0+T0
t
2 t
jm 2
jn
j 2
(mn)t
T0
T0
m (t), n (t) =
e
e
dt =
e T0
dt
t
t
0
0
t0 +T0
dt,
m=n
t0
t0 +T0
=
cos[2(m n)t/T0]
t0
+ j sin[2(m n)t/T0] dt, m = n
T0, m = n
=
0, m = n
We also conclude that cn = T0
Complex exponential Fourier series summary:

x(t) =
n=
1
where X n =
T0
X n e jn0t , t0 t t0 + T0
T0
x(t)e jn0t
The Fourier series expansion is unique
Example 2.6: x(t) = cos2 0t

If we expand x(t) into complex exponentials we can immediately determine the Fourier coefficients
1 1
x(t) = + cos 20t
2 2
1 1
1
= + e j20t + e j20t
2 4
4
2-21
The above implies that

Xn =
2,
1
,
4
0,
n=0
n = 2
otherwise
Time Average Operator

The time average of signal v(t) is defined as
T
1
v(t) = lim
v(t) dt
T 2T T
Note that
av 1(t) + bv 2(t) = av 1(t) + bv 2(t),
where a and b are arbitrary constants
If v(t) is periodic, with period T0, then
1
v(t) =
v(t) dt
T0 T0
The Fourier coefficients can be viewed in terms of the time
average operator
Let v(t) = x(t)e jn0t using e j = cos j sin , we find
that
X n = v(t) = x(t)e jn0t
= x(t) cos n0t jx(t) sin n0t
2-22
2.4. FOURIER SERIES
2.4.2
Symmetry Properties of the Fourier Coefficients
For x(t) real, the following coefficient symmetry properties

hold:
1. X n = X n
2. |X n | = |X n |
3.
X n = X n
proof
1
X n =
x(t)e jn0t dt
T0 T0
1
=
x(t)e j (n)0t dt = X n
T0 T0
since x (t) = x(t)
Waveform symmetry conditions produce special results too
1. If x(t) = x(t) (even function), then

X n = Re X n , i.e., Im X n = 0
2. If x(t) = x(t) (odd function), then

X n = Im X n , i.e., Re X n = 0
3. If x(t T0/2) = x(t) (odd half-wave symmetry), then

X n = 0 for n even
2-23
Example 2.7: Odd Half-wave Symmetry Proof

Consider
1
Xn =
T0
t0 =T0 /2
1
x(t)e jn0t dt +
T0
t0
t0 +T0
t0 +T0 /2
x(t )e jn0t dt
In the second integral we change variables by letting t = t

T0/2
1
Xn =
T0
t0
1
+
T0
t0 +T0 /2
x(t)e jn0t dt
t+T0 /2
t0
= 1e
x(t T0/2) e jn0(t+T0/2) dt

jn0 T0 /2
x(t)
1
T0
t0
t0 +T0 /2
x(t)e jn0t dt
but n0(T0/2) = n(2/T0)(T0/2) = n , thus

1 e jn =
2,
n odd
0,
n even
We thus see that the even indexed Fourier coefficients are indeed zero under odd half-wave symmetry
2-24
2.4. FOURIER SERIES
2.4.3
Trigonometric Form
The complex exponential Fourier series can be arranged as follows

x(t) =
X n e jn0t
n=
= X0 +
n=1
X n e jn0t + X n e jn0t
For real x(t), we may know that |X n | = |X n | and X n =

X n , so
x(t) = X 0 +
|X n |e
n=1
= X0 + 2
n=1
j[n0 t+ X n ]
+ |X n |e
j[n0 t+ X n ]
|X n | cos n0t + X n
since cos(x) = (e j x + e j x )/2

From the trig identity cos(u + v) = cos u cos v sin u sin v, it
follows that
x(t) = X 0 +
n=1
An cos(n0t) +
Bn sin(n0t)
n=1
where
An = 2x(t) cos(n0t)
Bn = 2x(t) sin(n0t)
2-25
2.4.4
Parsevals Theorem
Fourier series analysis are generally used for periodic signals,

i.e., x(t) = x(t + nT0) for any integer n
With this in mind, Parsevals theorem becomes
1
2
P=
|x(t)| dt =
|X n |2
T0 T0
n=
=
X 02
+2
n=1
|X n |2
(W)
Note: A 1 ohm system is assumed
2.4.5
Line Spectra
Line spectra was briefly reviewed earlier for simple signals

For any periodic signal having Fourier series representation we
can obtain both single-sided and double-sided line spectra
The double-sided magnitude and phase line spectra is most
easily obtained form the complex exponential Fourier series,
while the single-sided magnitude and phase line spectra can be
obtained from the trigonometric form
Double-sided
X n e j2(n f0)t
mag. and phase
n=
Single-sided
X 0 + 2
|X n | cos[2(n f 0)t + X n ]
mag. and phase
n=1
2-26
2.4. FOURIER SERIES
For the double-sided simply plot as lines |X n | and X n

versus n f 0 for n = 0, 1, 2, . . .
For the single-sided plot |X 0| and X 0 as a special case

for n = 0 at n f 0 = 0 and then plot 2|X n | and X 0 versus
n f 0 for n = 1, 2, . . .
Example 2.8: Cosine Squared

Consider
A A
+ cos 2(2 f 0)t + 21
2
2
A
+ e j21 e j2(2 f0)t
4
x(t) = A cos2(2 f 0t + ) =
=
A A j21 j2(2 f0)t

+ e e
2
4
DoubleSided
-2f0
2f0
-2f0
2f0
SingleSided
2f0
2f0
2-27
Example 2.9: Pulse Train

x(t)
A
...
-2T0
-T0
...
0
T0 T0 +
Periodic pulse train
The pulse train signal is mathematically described by
t nT0 /2
x(t) =
A
n=
The Fourier coefficients are
1 j2(n f0)t
A e j2(n f0)t
Xn =
Ae
dt =
T0 0
T0 j2(n f 0) 0
A 1 e j2(n f0)
=
T0
j2(n f 0)
A e j(n f0) e j(n f0) j(n f0)
=
e
T0
(2 j)(n f 0)
A sin[(n f 0) ] j(n f0)
=
e
T0
[(n f 0) ]
To simplify further we define
sinc(x) =
2-28
sin( x)
x
2.4. FOURIER SERIES
Finally,
Xn =
A
sinc(n f 0 )e j(n f0) , n = 0, 1, 2, . . .
T0
To plot the line spectra we need to find |X n | and X n

A
|sinc[(n f o ) ]|
T
0
(n f 0),
X n = (n f 0) + ,
(n f 0) ,
|X n | =
sinc(n f o ) > 0
n f 0 > 0 and sinc(n f 0 ) < 0
n f 0 < 0 and sinc(n f 0 ) < 0
Plot some double-sided line spectra example using MATLAB

First we create a helper function that takes as input a vector of
frequency values n f 0 and the coefficients X n
function Line_Spectra(fk,Xk,mode)
% Line_Spectra(fk,Xk,mode1) (file Line_Spectra.m)
%
% Plot Double-Sided Line Spectra
%---------------------------------------------------%
fk = vector of real sinusoid frequencies
%
Xk = magnitude and phase at each frequency in fk
%
mode = mag or phase plot
%
% % Mark Wickert, January 2007
switch lower(mode) % not case sensitive
case mag,magnitude % two choices work
stem(fk,abs(Xk),filled);
grid
axis([-1.05*max(fk) 1.05*max(fk) 0 1.05*max(abs(Xk))])
ylabel(Magnitude)
xlabel(Frequency (Hz))
case phase
stem(fk,angle(Xk),filled);
grid
axis([-1.05*max(fk) 1.05*max(fk), ...
-1.1*max(abs(angle(Xk))) 1.1*max(abs(angle(Xk)))])
ylabel(Phase (rad))
2-29
xlabel(Frequency (Hz))
otherwise
error(mode must be mag or phase)
end
As a specific example enter the following at the MATLAB command prompt

>>
>>
>>
>>
>>
>>
>>
n = -25:25;
tau = 0.125; f0 = 1; A = 1;
Xn = A*tau*f0*sinc(n*f0*tau).*exp(-j*pi*n*f0*tau);
subplot(211)
Line_Spectra(n*f0,Xn,mag)
subplot(212)
Line_Spectra(n*f0,Xn,phase)
Af0 = 0.125
Magnitude
0.1
f0 = 1, = 0.125
1/ = 8
0.05
0
25
20
15
10
5
0
5
Frequency (Hz)
10
15
20
25
20
15
10
5
0
5
Frequency (Hz)
10
15
20
25
Phase (rad)
2
0
2
25
2-30
2.4. FOURIER SERIES
2.4.6
Numerical Calculation of X n
Here we consider a purely numerical calculation of the X k coefficients from a single period waveform description of x(t)
In particular, we will use MATLABs fast Fourier transform
(FFT) function to carry out the numerical integration
By definition
1
Xk =
T0
T0
x(t)e j2 k f0t dt, k = 0, 1, 2, . . .
A simple rectangular integration approximation to the above

integral is
N 1
1
T0
Xk
x(nT )e jk2(n f0)T0/N , k = 0, 1, 2, . . .
T0 n=0
N
where N is the number of points used to partition the time
interval [0, T0] and T = T0/N is the time step
Using the fact that 2 f 0 T0 = 2 , we can write that
N 1
j2 kn
1
Xk
x(nT )e N , k = 0, 1, 2, . . .
N n=0
Note that the above must be evaluated for each Fourier coefficient of interest
Also note that the accuracy of the X k values depends on the
value of N
2-31
For k small and x(t) smooth in the sense that the harmonics rolloff quickly, N on the order of 100 may be adequate
For k moderate, say 550, N will have to become increasingly larger to maintain precision in the numerical integral
Calculation Using the FFT
The FFT is a powerful digital signal processing (DSP) function, which is a computationally efficient version of thediscrete
Fourier transfrom (DFT)
For the purposes of the problem at hand, suffice it to say that
the FFT is just an efficient algorithm for computing
X [k] =
N 1
n=0
x[n]e j2kn/N , k = 0, 1, 2, . . . , N 1
If we let x[n] = x(nT ), then it should be clear that

Xk
1
N
X [k], k = 0, 1, . . . ,
N
2
To obtain X k for k0 note that

X k
N 1
j2(k)n
1
1
X [k] =
x(nT )e N
N
N n=0
N 1
j2(N k)n
1
=
x(nT )e N
= X [N k]
N n=0
since e j2 N n/N = e j2 n = 1
2-32
2.4. FOURIER SERIES
In summary
Xk
X [k]/N ,
X [N k]/N ,
0 k N /2
N /2 k < 0
To use the MATLAB function fft() to obtain the X k we simply let

X = fft(x)
where x = {x(t) : t = 0, T0/N , 2T0/N , . . . , T0(N 1)/N }
Remember in MATLAB that X [0] is really found in X[1], etc.
Example 2.10: Finite Rise/Fall-Time PulseTrain

x(t)
1
Pulse width =
Rise and fall time = tr
1/2
tr
+ tr
T0
Pulse train with finite rise and fall time edges
Shown above is one period of a finite rise and fall time pulse
train
We will numerically compute the Fourier series coefficients of
this signal using the FFT
The MATLAB function trap pulse was written to generate
one period of the signal using N samples
2-33
function [xp,t] = trap_pulse(N,tau,tr)

% xp = trap_pulse(N,tau,tr)
%
% Mark Wickert, January 2007
n = 0:N-1;
t = n/N;
xp = zeros(size(t));
% Assume tr and tf are equal
T1 = tau + tr;
% Create one period of the trapezoidal pulse waveform
for k=1:N
if t(k) <= tr
xp(k) = t(k)/tr;
elseif (t(k) > tr & t(k) <= tau)
xp(k) = 1;
elseif (t(k) > tau & t(k) < T1)
xp(k) = -t(k)/tr+ 1 + tau/tr;
else
xp(k) = 0;
end
end
We now plot the double-sided line spectra for = 1/8 and two
values of rise-time tr
>>
>>
>>
>>
>>
>>
>>
>>
>>
>>
>>
>>
>>
>>
>>
>>
>>
>>
% tau = 1/8, tr = 1/20

N = 1024;
[xp,t] = trap_pulse(N,1/8,1/20);
Xp = fft(xp);
subplot(211)
plot(t,xp)
grid
ylabel(x(t))
xlabel(Time (s))
subplot(212)
Xp_shift = fftshift(Xp)/N;
f = -N/2:N/2-1;
Line_Spectra(f,Xp_shift,mag)
axis([-25 25 0 .15])
print -tiff -depsc line_spec2.eps
% tau = 1/8, tr = 1/10
xp = trap_pulse(N,1/8,1/10);
Xp = fft(xp);
2-34
2.4. FOURIER SERIES
>>
>>
>>
>>
>>
>>
>>
>>
>>
>>
>>
Xp_shift = fftshift(Xp)/N;
f = N/2:N/2-1;
subplot(211)
plot(t,xp)
grid
ylabel(x(t))
xlabel(Time (s))
subplot(212)
Line_Spectra(f,Xp_shift,mag)
axis([-25 25 0 .15])
print -tiff -depsc line_spec3.eps
x(t)
0.8
1/20
0.6
f0 = 1, = 0.125, tr = 1/20
1/8
0.4
0.2
0
0.1
0.2
0.3
0.4
0.5
0.6
Time (s)
0.7
0.8
0.9
20
25
Magnitude
0.15
0.1
0.05
0
25
Sidelobes smaller
than ideal pulse train
which has zero rise
time
20
15
10
1/ = 1/8
5
0
5
Frequency (Hz)
10
15
Signal x(t) and line spectrum for = 1/8 and tr = 1/20

2-35
x(t)
0.8
1/10
f0 = 1, = 0.125, tr = 1/10
0.6
1/8
0.4
0.2
0
0.1
0.2
0.3
0.4
0.5
0.6
Time (s)
0.7
0.8
0.9
20
25
Magnitude
0.15
0.1
Sidelobes smaller
than with tr = 1/20
case
1/ = 1/8
0.05
0
25
20
15
10
5
0
5
Frequency (Hz)
10
15
Signal x(t) and line spectrum for = 1/8 and tr = 1/10
2-36
2.4. FOURIER SERIES
2.4.7
Other Fourier Series Properties
Given x(t) has Fourier series (FS) coefficients X n , if

y(t) = A + Bx(t)
it follows that
Yn =
proof:
A + B X 0,
B Xn,
n=0
n = 0
Yn = y(t)e j2(n f0)t

= Ae j2(n f0)t + Bx(t)e j2(n f0)t
1, n = 0
=A
+ B Xn
0, n = 0
Likewise if
QED
y(t) = x(t t0)
it follows that
Yn = X n e j2(n f0)t0
proof:
Yn = x(t t0)e j2(n f0)t
Let = t t0 which implies also that t = + t0, so

Yn = x()e j2(n f0)(+t0)
= x()e j2(n f0)e j2(n f0)t0
= X n e j2(n f0)t0
QED
2-37
2.5
Fourier Transform
The Fourier series provides a frequency domain representation

of a periodic signal via the Fourier coefficients and line spectrum
The next step is to consider the frequency domain representation of aperiodic signals using the Fourier transform
Ultimately we will be able to include periodic signals within
the framework of the Fourier transform, using the concept of
transform in the limit
The text establishes the Fourier transform by considering a
limiting case of the expression for the Fourier series coefficient
X n as T0
The Fourier transform (FT) and inverse Fourier transfrom (IFT)
is defined as

X( f ) =
x(t)e j2 f t dt (FT)
x(t) =
X ( f )e j2 f t d f (IFT)
Sufficient conditions for the existence of the Fourier transform

are
1. |x(t)| dt <
2. Discontinuities in x(t) be finite
3. An alternate sufficient condition is that |x(t)|2 dt <

, which implies that x(t) is an energy signal
2-38
2.5. FOURIER TRANSFORM
2.5.1
Amplitude and Phase Spectra
FT properties are very similar to those obtained for the Fourier

coefficients of periodic signals
The FT, X ( f ) = F{x(t)}, is a complex function of f
X ( f ) = |X ( f )|e j( f ) = |X ( f )|e j
= Re{X ( f )} + jIm{X ( f )}
X( f )
The magnitude |X ( f )| is referred to as the amplitude spectrum

The the angle X ( f ) is referred to as the phase spectrum
Note that
Re{X ( f )} =
Im{X ( f )} =
2.5.2
x(t) cos 2 f t dt
x(t) sin 2 f t dt
Symmetry Properties
If x(t) is real it follows that

X ( f ) =
x(t)e j2( f )t dt

=
x(t)e j2 f t dt = X ( f )
thus
|X ( f )| = |X ( f )| (even in frequency)
X ( f ) = X ( f ) (odd in frequency)
2-39
Additionally,
1. For x(t) = x(t) (even function), Im{X ( f )} = 0
2. For x(t) = x(t) (odd function), Re{X ( f )} = 0
2.5.3
Energy Spectral Density
From the definition of signal energy,

E=
|x(t)|2 dt

=
x (t)
X ( f )e j2 f t d f dt
=
X( f )
x (t)e j2 f t dt d f
but
x (t)e j2 f t dt =
Finally,
E=
x(t)e j2 f t dt
|x(t)| dt =
= X ( f )
|X ( f )|2 d f
which is known as Rayleighs Energy Theorem

Are the units consistent?
Suppose x(t) has units of volts
|X ( f )|2 has units of (volts-sec)2
2-40
In a 1 ohm system |X ( f )|2 has units of Watts-sec/Hz =

Joules/Hz
The energy spectral density is defined as
G( f ) = |X ( f )|2 Joules/Hz
It then follows that
E=
G( f ) d f
Example 2.11: Rectangular Pulse

Consider
t t0
x(t) = A
FT is
X( f ) = A
t0 +/2
t0 /2
e j2 f t dt
t +/2
e j2 f t 0
= A
j2 f t0/2
j f
e
e j f
= A
e j2 f t0
( j2) f
= A sinc( f )e j2 f t0
t t0
F
A
A sinc( f )e j2 f t0
Plot |X ( f )|, X ( f ), and G( f )

2-41
A1
Amplitude
Spectrum
|X(f)| 0.8
Phase
Spectrum
0.6
0.4
?3
0.2
?3
?2
-2/
?1
-1/
1/1
2
2/
2
1
/2
? 1-1/
?1
/2
?2
t0 = /2
?3
(A)12
G(f) = |X(f)|2
-2/? 2
X(f) 3
11/
2/
2
slope = -f/2
Energy
Spectral
Density
0.8
0.6
0.4
0.2
?3
?2
-2/
?1
-1/
1/1
2
2/
Rectangular pulse spectra
2.5.4
Transform Theorems
Be familiar with the FT theorems found in the table of Appendix G.6 of the text
Superposition Theorem
F
proof:
2-42
a1 x1(t) + a2 x2(t) a1 X 1( f ) + a2 X 2( f )
Time Delay Theorem

F
x(t t0) X ( f )e j2 f t0
proof:
Frequency Translation Theorem

In communications systems the frequency translation and modulation theorems are particularly important
F
x(t)e j2 f0t X ( f f 0)
proof: Note that

x(t)e j2 f0t e j2 f t dt =
so
F x(t)e
j2 f 0 t
x(t)e j2( f f0)t dt
= X ( f f 0)
QED
Modulation Theorem
The modulation theorem is an extension of the frequency translation theorm
1
1
F
x(t) cos(2 f 0t) X ( f f 0) + X ( f + f 0)
2
2
2-43
proof: Begin by expanding

1
1
cos(2 f 0t) = e j2 f0t + e j2 f0t
2
2
Then apply the frequency translation theorem to each term separately
X(f)
signal
multiplier
x(t)
Y(f)
y(t)
A/2
-f0
cos(2f0t)
f0
A simple modulator
Duality Theorem
Note that
F{X (t)} =
X (t)e
j2 f t
dt =
X (t)e j2( f )t dt
which implies that

F
X (t) x( f )
2-44
Example 2.12: Rectangular Spectrum

X(f)
-W
Using duality on the above we have
t
F
X (t) =
2W sinc(2W f ) = x( f )
2W
Since sinc( ) is an even function (sinc(x) = sinc(x)), it follows that
f
F
2W sinc(2W t)
2W
Differentiation Theorem
The general result is
d n x(t) F
n
(
j2
f
)
X( f )
dt n
proof: For n = 1 we start with the integration by parts formula,

u dv = uv v du, and apply it to

dx
d x j2 f t
F
=
e
dt
dt
dt
= x(t)e j2 f t + j2 f
x(t)e j2 f t dt
X( f )
2-45
alternate From Leibnitzs rule for differentiation of integrals,

d
F( f, t)
F( f, t) d f =
df
dt
so
d x(t)
d
=
X ( f )e j2 f t d f
dt
dt

e j2 f t
=
X( f )
df
t

=
j2 f X ( f )e j2 f t d f
d x/dt j2 f X ( f )
QED
Example 2.13: FT of Triangle Pulse

1
Note that
1/
1/
-1/
2-46
-2/
Using the differentiation theorem for n = 2 we have that

1
t
1
2
1
F
=
F (t + ) (t) + (t )
( j2 f )2
1 j2 f
e
2 + 1 e j2 f
=
( j2 f )2
2 cos(2 f ) 2
=
(2 f )2
4 sin2( f )
2
=
=
sinc
( f )
4( f )2

t
F
sinc2( f )
Convolution and Convolution Theorem

Before discussing the convolution theorem we need to review
convolution
The convolution of two signals x1(t) and x2(t) is defined as

x(t) = x1(t) x2(t) =
x1()x2(t ) d
= x2(t) x1(t) =
x2()x1(t ) d
A special convolution case is (t t0)

(t t0) x(t) =
( t0)x(t ) d
= x(t )=t0 = x(t t0)

2-47
Example 2.14: Rectangular Pulse Convolution

Let x1(t) = x2(t) = (t/ )
To evaluate the convolution integral we need to consider the
integrand by sketching of x1() and x2(t ) on the axis for
different values of t
For this example four cases are needed for t to cover the entire
time axis t (, )
Case 1: When t < we have no overlap so the integrand is
zero and x(t) is zero
x2(t - )
t - /2
t + /2
x1()
/2
No overlap for t +
/2 < -/2 or t <
/2
Case 2: When < t < 0 we have overlap and

x(t) =
x1()x2(t ) d
t+/2
t+/2
=
d =
/2
/2
= t + /2 + /2 = + t
x2(t - )
0
/2
t + /2
2-48
x1()
/2
Overlap begins when t

+ /2 = -/2 or t = -
Case 3: For 0 < t < the leading edge of x2(t ) is to the

right of x1(), but the trailing edge of the pulse is still overlapped
/2
x(t) =
d = /2 t + /2 = t
t/2
x2(t - )
x1()
Overlap lasts until t =
/2
/2
t - /2
t + /2
Case 4: For t > we have no overlap, and like case 1, the

result is
x(t) = 0
x2(t - )
x1()
No overlap for t >
/2
/2
t - /2
t + /2
Collecting the results
0,
+ t,
x(t) =
t,
0,
|t|,
=
0,
t <
t < 0
0t <
t
|t|
otherwise
2-49
Final summary,

t
t
t
Convolution Theorem: We now consider x1(t)x2(t) in terms

of the FT

x1( )x2(t ) d

=
x1( )
X 2( f )e j2 f (t ) d f d
=
X 2( f )
x1( )e j2 f d e j2 f t d f
=
X 1( f )X 2( f )e j2 f t d f
which implies that
x1(t) x2(t) X 1( f )X 2( f )
Example 2.15: Revisit (t/ ) (t/ )

Knowing that (t/ )(t/ ) = (t/ ) in the time domain,
we can follow-up in the frequency domain by writing

2
F (t/ ) F (t/ ) = sinc( f )
2-50
We have also established the transform pair

t
F
2sinc2( f ) = sinc2( f )
or

t
F
sinc2( f )
Multiplication Theorem
Having already established the convolution theorem, it follows
from the duality theorem or direct evaluation, that
F
x1(t) x2(t) X 1( f ) X 2( f )
2.5.5
Fourier Transforms in the Limit
thus far we have considered two classes of signals

1. Periodic power signals which are described by line spectra
2. Non-periodic (aperiodic) energy signals which are described
by continuous spectra via the FT
We would like to have a unifying approach to spectral analysis
To do so we must allow impulses in the frequency domain by
using limiting operations on conventional FT pairs, known as
Fourier transforms-in-the-limit
Note: The corresponding time functions have infinite energy, which implies that the concept of energy spectral
density will not apply for these signals (we will introduce
the concept of power spectral density for these signals)
2-51
Example 2.16: A Constant Signal

Let x(t) = A for < t <
We can write
x(t) = lim A(t/T )

T
Note that
F A(t/T ) = AT sinc( f T )
Using the transform-in-the-limit approach we write

F{x(t)} = lim AT sinc( f T )
T
1
0.8
?3
?2
?1
AT1
1
0.8
0.6
0.6
0.4
0.4
0.2
0.2
? 0.2
3 ?3
?2
?1
AT2
T2 >> T1
? 0.2
Increasing T in AT sinc( f T )
Note that since x(t) has no time variation it seems reasonable

that the spectral content ought to be confined to f = 0
Also note that it can be shown that

AT sinc( f T ) d f = A,
Thus we have established that

F
A A( f )
2-52
As a further check
F 1 A( f ) =
A( f )e
j2 f f t
d f = Ae
j2 f t
f =0
=A
As a result of the above example, we can obtain several more

FT-in-the-limit pairs
F
Ae j2 f0t A( f f 0)
A j
F
e ( f f 0) + e j ( f + f 0)
A cos(2 f 0t + )
2
F
A(t t0) Ae j2 f t0
Reciprocal Spreading Property: Compare
F
A(t) A
and
A A( f )
A constant signal of infinite duration has zero spectral width,

while an impulse in time has zero duration and infinite spectral
width
2.5.6
Fourier Transforms of Periodic Signals
For an arbitrary periodic signal with Fourier series

x(t) =
X n e j2 n f0t
n=
2-53
we can write
X( f ) = F
=
=
X n e j2n f0t
n=
n=
n=
XnF e
j2 n f 0 t
X n ( f n f 0)
using superposition and F{Ae j2 f0t } = A( f f 0)

What is the difference between line spectra and continuous
spectra? none!
Mathematically,
Line
Spectra
Continuous
Spectra
Convert to
time domain
Sum phasors
Convert to
time domain
Integrate impulses to
get phasors via the
inverse FT
The Fourier series coefficients need to be known before the FT

spectra can be obtained
A technique that obtained the FT directly will be discussed
later
2-54
Example 2.17: Ideal Sampling Waveform

When we discuss sampling theory it will be useful to have the
FT of the periodic impulse train signal
ys (t) =
m=
(t mTs )
where Ts is the sample spacing or period

Since this signal is periodic, it must have a Fourier series representation too
In particular
1
Yn =
Ts
Ts
(t)e j2(n fs )t dt =
1
= f s , any n
Ts
where f s is the sampling rate in Hz

The FT of ys (t) is given by
Ys ( f ) = f s
n=
F e
j2 n f 0 )t
= fs
n=
( f n f s )
Summary,
m=
(t mTs ) f s
n=
( f n f s )
2-55
ys(t)
...
...
0
-Ts
Ys(f)
Ts
fs
...
...
-fs
4Ts
4fs
fs
An impulse train in times is an impulse train in frequency
Example 2.18: Convolve Step and Exponential

Find y(t) = Au(t) et u(t), > 0
For tleq0 there is no overlap so Y (t) = 0
No overlap
t
2-56
For t > 0 there is always overlap

y(t) =
t
0
A e(t) d
= Aet
= Aet
e t
0
et 1
For t > 0 there is

always overlap
0
Summary,
y(t) =
A
1 et u(t)
A/
y(t)
2-57
Direct Approach for the FT of a Periodic Signal

The FT of a periodic signal can be found directly by expanding
x(t) as follows

x(t) =
(t mTs ) p(t) =
p(t mTs )
m=
m=
where p(t) represents one period of x(t), having period Ts

From the convolution theorem

X( f ) = F
(t mTs ) P( f )
m=
= f s P( f )
= fs
n=
n=
( f n f s )
P(n f s )( f n f s )
where P( f ) = F{p(t)}
The FT transform pair just established is
m=
2-58
p(t mTs )
n=
f s P(n f s )( f n f s )
Example 2.19: p(t) = (t/2) + (t/4), T0 = 10

x(t)
2
...
1
-2
-1
...
T0 = 10
Stacked pulses periodic signal
We begin by finding P( f ) using F{(t/ )} = sinc( f )

P( f ) = 2sinc(2 f ) + 4sinc(4 f )
Plugging into the FT pair derived above with n f s = n/10,

n
1
2n
n
X( f ) =
2sinc
+ 4sinc
f
10 n=
5
5
10
2.5.7
Poisson Sum Formula
The Poisson sum formula from mathematics can be derived

using the FT pair
F
e j2(n fs )t ( f n f s )
by writing

F 1
f s P(n f s )( f n f s ) = f s
P(n f s )e j2(n fs )t
n=
n=
2-59
From the earlier developed FT of periodic signals pair, we

know that the left side of the above is also equal to
m=
also
p(t mTs ) = f s
P(n f s )e j2(n fs )t
n=
We can finally relate this back to the Fourier series coefficients,

i.e.,
X n = f s P(n f s )
2.6
Power Spectral Density and Correlation
For energy signals we have the energy spectral density, G( f ),

defined such that

E=
G( f ) d f
For power signals we can define the power spectral density

(PSD), S( f ) of x(t) such that

P=
S( f ) d f = |x(t)|2
Note: S( f ) is real, even and nonnegative
If x(t) is periodic S( f ) will consist of impulses at the

harmonic locations
For x(t) = A cos(0t + ), intuitively,
S( f ) =
2-60
1 2
1
A ( f f 0) + A2( f + f 0)
4
4
2.6. POWER SPECTRAL DENSITY AND CORRELATION
since S( f ) d f = A2/2 as expected (power on a per ohm

basis)
To derive a general formula for the PSD we first need to consider the autocorrelation function
2.6.1
The Time Average Autocorrelation Function
Let ( ) be the autocorrelation function of an energy signal
( ) = F 1 G( f )
= F 1 X ( f )X ( f )
= F 1 X ( f ) F 1 X ( f )
but x(t) X ( f ) for x(t) real, so

( ) = x(t) x(t) =
x(t)x(t + ) d
or
( ) = lim
Observe that
x(t)x(t + ) d
G( f ) = F ( )
The autocorrelation function (ACF) gives a measure of the

similarity of a signal at time t to that at time t + ; the coherence between the signal and the delayed signal
2-61
X(f)
G(f) = |X(f)|2
x(t)
() =
Energy spectral density and signal relationships
2.6.2
Power Signal Case
For power signals we define the autocorrelation function as

Rx ( ) = x(t)x(t + )
T
1
= lim
x(t)x(t + ) dt
T 2T T
if periodic 1
=
x(t)x(t + ) dt
T0 T0
Note that
2
Rx (0) = |x(t)| =
Sx ( f ) d f
and since for energy signals ( ) G( f ), a reasonable

assumption is that
F
Rx ( ) Sx ( f )
2-62
A formal statement of this is the Wiener-Kinchine theorem (a

proof is given in text Chapter 5)

Sx ( f ) =
Rx ( )e j2 f d
x(t)
Rx()
Sx(f)
Power spectral density and signal relationships
2.6.3
Properties of R( )
The following properties hold for the autocorrelation function

1. R(0) = |x(t)|2 |R( )| for all values of
2. R( ) = x(t)x(t ) = R( ) an even function

3. lim| | R( ) = x(t)2 if x(t) is not periodic
4. If x(t) is periodic, with period T0, then R( ) = R( + T0)

5. F{R( )} = S( f ) 0 for all values of f
The power spectrum and autocorrelation function are frequently

used for systems analysis with random signals
2-63
Example 2.20: Single Sinusoid

Consider the signal x(t) = A cos(2 f 0t + ), for all t
1 T0 2
Rx ( ) =
A cos(2 f 0t + ) cos(2(t + ) + ) dt
T0 0
A2
=
cos(2 f 0 ) + cos(2(2 f 0)t + 2 f 0 + 2) dt
2T0 T0
A2
=
cos(2 f 0 )
2
Note that
A2
F Rx ( ) = Sx ( f ) =
( f f 0) + ( f + f 0)
4
More Autocorrelation Function Properties
Suppose that x(t) has autocorrelation function Rx ( )
Let y(t) = A + x(t), A = constant
R y ( ) = [A + x(t)][A + x(t + )]
= A2 + Ax(t + ) + Ax(t) + x(t)x(t + )
= A2 + 2Ax(t) +Rx ( )
const. terms
Let z(t) = x(t t0)
Rz ( ) = z(t)z(t + ) = x(t t0)x(t t0 +

= x()x( + ), with = t t0
= Rx ( )
2-64
The last result shows us that the autocorrelation function is

blind to time offsets
Example 2.21: Sum of Two Sinusoids

Consider the sum of two sinusoids
y(t) = x1(t) + x2(t)
where x1(t) = A1 cos(2 f 1t +1) and x2(t) = A2 cos(2 f 2t +
2) and we assume that f 1 = f 2
Using the definition
R y ( ) = [x1(t) + x2(t)][x1(t + )x2(t + )]
= x1(t)x1(t + ) + x2(t)x2(t + )
+ x1(t)x2(t + ) + x2(t)x1(t + )
The last two terms are zero since cos((1 2)t) = 0 when
f 1 = f 2 (why?), hence
R y ( ) = Rx1 ( ) + Rx2 ( ), for f 1 = f 2
A21
A22
=
cos(2 f 1 ) +
cos(2 f 2 )
2
2
Example 2.22: PN Sequences

In the testing and evaluation of digital communication systems
a source of known digital data (i.e., 1s and 0s) is required
(see text Chapter 8 p. 429432)
2-65
A maximal length sequence generator or pseudo-noise (PN)

code is often used for this purpose
Practical implementation of a PN code generator can be accomplished using an N -stage shift register with appropriate
exclusive-or feedback connections
The sequence length or period of the resulting PN code is M =
2 N 1 bits long
Clock
Period = T
D1
Q1
D2
Q2
D3
x(t)
Q3
M = 23 - 1 = 7
x(t)
+A
t
-A
one period = NT
Three stage PN (m-sequence) generator
PN sequences have quite a number of properties, one being that

the time average autocorrelation function is of the form shown
below
2-66
Rx()
A2
MT
...
-T
...
T
MT
-A2/M
PN sequence autocorrelation function
The calculation of the power spectral density will be left as a

homework problem
Hint: To find Sx ( f ) = F{Rx ( )} we use
F
p(t nTs ) f s
P(n f s )( f n f s )
n
where Ts = M T
One period of Rx ( ) is a triangle pulse with a level shift

Suppose the logic levels are switched from A to positive levels of say v 1 to v 2
Using the additional autocorrelation function properties
this can be done
You need to know that a PN sequence contains one more
1 than 0
MATLAB for generating PN sequences from 2 to 12 stages is
given below
function c = m_seq(m)
%function c = m_seq(m)
%
% Generate an m-sequence vector using an all-ones initialization
%
2-67
% Mark Wickert, April 2005

sr = ones(1,m);
Q = 2m - 1;
c = zeros(1,Q);
switch m
case 2
taps = [1 1 1];
case 3
taps = [1 0 1 1];
case 4
taps = [1 0 0 1 1];
case 5
taps = [1 0 0 1 0 1];
case 6
taps = [1 0 0 0 0 1 1];
case 7
taps = [1 0 0 0 1 0 0 1];
case 8
taps = [1 0 0 0 1 1 1 0 1];
case 9
taps = [1 0 0 0 0 1 0 0 0 1];
case 10
taps = [1 0 0 0 0 0 0 1 0 0 1];
case 11
taps = [1 0 0 0 0 0 0 0 0 1 0 1];
case 12
taps = [1 0 0 0 0 0 1 0 1 0 0 1 1];
otherwise
disp(Invalid length specified)
end
for n=1:Q,
tap_xor = 0;
c(n) = sr(m);
for k=2:m,
if taps(k) == 1,
tap_xor = xor(tap_xor,xor(sr(m),sr(m-k+1)));
end
end
sr(2:end) = sr(1:end-1);
sr(1) = tap_xor;
end
2-68
R( ), S( f ), and Fourier Series

For a periodic power signal, x(t), we can write
x(t) =
X n e j2(n f0)t
n=
There is an interesting linkage between the Fourier series representation of a signal, the power spectrum, and then back to
the autocorrelation function
Using the orthogonality properties of the Fourier series expansion we can write

j2(n f 0 )t
R( ) =
Xne
X m e j2(m f0)t
=
=
n=
m=
X n X m
j2(nm) f0t
e
n= m=
|X n |2e j2(n f0)t

n=
The power spectral density can be obtained by Fourier transforming both sides of the above
S( f ) =
n=
|X n |2( f n f 0)
2-69
2.7
Linear Time Invariant (LTI) Systems

y(t) =
x(t)
operator
Linear system block diagram
Definition
Linearity (superposition) holds, that is for input 1 x1(t)+2 x2(t),
1 and 2 constants,
y(t) = H 1 x1(t) + 2 x2(t)
= 1H x1(t) + 2H x2(t)
= 1 y1(t) + 2 y2(t)
A system is time invariant (fixed) if for y(t) = H[x(t)], a
delayed input gives a correspondingly delayed output, i.e.,
y(t t0) = H x(t t0)
Impulse Response and Superposition Integral
The impulse response of an LTI system is denoted
h(t) = H (t)
assuming the system is initially at rest
Suppose we can write x(t) as

x(t) =
2-70
n=1
n (t tn )
2.7. LINEAR TIME INVARIANT (LTI) SYSTEMS
For an LTI system with impulse response h( )

N
y(t) =
n=1
n h(t tn )
To develop the superposition integral we write

x(t) =
x()(t ) d
lim
n=N
x(nt)(t nt) t, for t 1
Rectangle area is approximation
x(t)
...
...
0
2t
3t
4t
5t
6t
Impulse sequence approximation to x(t)
If we apply H to both sides and let t 0 such that nt

we have
y(t) lim
=
or
n=N
x(nt)h(t nt) t
x()h(t ) d = x(t) h(t)

x(t )h( ) d = h(t) x(t)
2-71
2.7.1
Stability
In signals and systems the concept of bounded-input boundedoutput (BIBO) stability is introduced
Satisfying this definition requires that every bounded-input (|x(t)| <
) produces a bounded output (|y(t)| < )
For LTI systems a fundamental theorem states that a system is
BIBO stable if and only if

|h(t)| dt <
Further implications of this will be discussed later
2.7.2
Transfer Function
The frequency domain result corresponding to the convolution

expression y(t) = x(t) h(t) is
Y ( f ) = X ( f )H ( f )
where H ( f ) is known as the transfer function or frequency
response of the system having impulse response h(t)
It immediately follows that
F
h(t) H ( f )
and
y(t) = F
2-72
X ( f )H ( f ) =
X ( f )H ( f )e j2 f t d f
2.7.3
Causality
A system is causal if the present output relies only on past and

present inputs, that is the output does not anticipate the input
The fact that for LTI systems y(t) = x(t) h(t) implies that
for a causal system we must have
h(t) = 0, t < 0
Having h(t) nonzero for t < 0 would incorporate future
values of the input to form the present value of the output
Systems that are causal have limitations are their frequency
response,
the PaleyWiener theorem states that
in particular
for |h(t)|2 dt < , H ( f ) for a cusal system must satisfy
| ln |H ( f )||
df <
2
1
+
f
In simple terms this means:

1. We cannot have |H ( f )| = 0 over a finite band of frequencies (isolated points ok)
2. The roll-off rate of |H ( f )| cannot be too great, e.g., ek1| f |
k2 | f |2
and
e
are not allowed, but polynomial forms such as
1/(1 + ( f / f c )2N , N an integer, are acceptable

3. Practical filters such as Butterworth, Chebyshev, and elliptical filters can come close to ideal requirements
2-73
2.7.4
Properties of H ( f )
For h(t) real it follows that

|H ( f )| = |H ( f )| and
H ( f ) = H ( f )
why?
Input/output relationships for spectral densities are
G y ( f ) = |Y ( f )|2 = |X ( f )H ( f )|2 = |H ( f )|2 G x ( f )
Sy ( f ) = |H ( f )|2 Sx ( f ) proof in text chap. 5
Example 2.23: RC Lowpass Filter

R
x(t)
X(f )
vc(t)
ic(t)
y(t)
Y(f )
h(t), H(f)
RC lowpass filter schematic
To find H ( f ) we may solve the circuit using AC steady-state

analysis
1
Y ( j)
1
jc
=
=
1
X ( j)
1 + j RC
R + jc
so
H( f ) =
2-74
Y( f )
1
=
, where f 3 = 1/(2 RC)
X ( f ) 1 + j f / f3
From the circuit differential equation

x(t) = i c (t)R + y(t)
but
i c (t) = c
dv c (t)
y(t)
=c
dt
dt
thus
RC
dy(t)
+ y(t) = x(t)
dt
F
FT both sides using d x/dt j2 f X ( f )

j2 f RCY ( f ) + Y ( f ) = X ( f )
so again
Y( f )
1
=
X ( f ) 1 + j f / f3
1
1
=
e j tan ( f / f3)
1 + ( f / f 3 )2
H( f ) =
The Laplace transfrom could also be used here, and perhaps is

preferred, we just need to substitute s j j2 f
2-75
-f3
f3
/2
f
-/2
RC lowpass frequency response
Find the system response to
(t T /2)
x(t) = A
T
Finding Y ( f ) is easy since
1
Y ( f ) = X ( f )H ( f ) = AT sinc( f T )
e j f t
1 + j f / fs
To find y(t) we can IFT the above, use Laplace transforms, or

convolve directly
From the FT tables we known that
h(t) =
2-76
1 t/(RC)
e
u(t)
RC
In Example 2.18 we showed that

Au(t) et u(t) =
Note that
t T /2
A
T
A
1 et u(t)
= A[u(t) u(t T )]
and here = 1/(RC), so
A
y(t) =
RC 1 et/(RC) u(t)
RC
RC 1 e(tT )/(RC) u(t T )

RC
RC =
|X(f)|, |H(f)|, |Y(f)|
T/1
0
T/
5
y(t)
1
0.8
0.6
T/
2
0.8
0.6
0.4
0.4
2T
0.2
0.5
|X(f)|, |H(f)|, |Y(f)|
0.2
1.5
2.5
t/T
-3
-2
-1
0.8
-1
fT
0.6
0.4
0.2
-2
0.8
RC = T/2
0.4
|X(f)|, |H(f)|, |Y(f)|
0.6
-3
RC = 2T
RC = T/10
0.2
1
fT
-3
-2
-1
fT
Pulse time response and frequency spectra with A = 1
2-77
2.7.5
Response to Periodic Inputs
When the input is periodic we can write
x(t) =
n=
which implies that

X( f ) =
It then follows that
Y( f ) =
and
y(t) =
=
n=
n=
X n e j2(n f0)t
n=
n=
X n ( f n f 0)
X n H (n f 0)( f n f 0)
X n H (n f 0)e j2(n f0)t

|X n ||H (n f 0|e j[2(n f0)t+
X n + H (n f 0 )]
This is a steady-state response calculation, since the analysis

assumes that the periodic signal was applied to the system at
t =
2.7.6
Distortionless Transmission
In the time domain a distortionless system is such that for any

input x(t),
y(t) = H0 x(t t0)
2-78
where H0 and t0 are constants

In the frequency domain the implies a frequency response of
the form
H ( f ) = H0e j2 f t0 ,
that is the amplitude response is constant and the phase shift is

linear with frequency
Distortion types:
1. Amplitude response is not constant over a frequency band
(interval) of interest amplitude distortion
2. Phase response is not linear over a frequency band of interest phase distortion
3. The system is non-linear, e.g., y(t) = k0 +k1 x(t)+k2 x 2(t)

nonlinear distortion
2.7.7
Group and Phase Delay
The phase distortion of a linear system can be characterized

using group delay, Tg ( f ),
Tg ( f ) =
1 d ( f )
2 d f
where ( f ) is the phase response of an LTI system

Note that for a distortionless system ( f ) = 2 f t0, so
Tg ( f ) =
1 d
2 f t0 = t0 s
2 d f
clearly a constant group delay

2-79
Tg ( f ) is the delay that two or more frequency components undergo in passing through an LTI system
If say Tg ( f 1) = Tg ( f 2) and both of these frequencies are
in a band of interest, then we know that delay distortion
exists
Having two different frequency components arrive at the
system output at different times produces signal dispersion
An LTI system passing a single frequency component, x(t) =
A cos(2 f 1t), always appears distortionless since at a single
frequency the output is just
y(t) = A|H ( f 1)| cos 2 f 1t + ( f 1)
( f 1)
= A|H1( f )| cos 2 f 1 t
2 f 1
which is equivalent to a delay known as the phase delay
Tp( f ) =
( f )
2 f
The system output now is
y(t) = A|H ( f 1)| cos 2 f 1(t T p ( f 1))]
Note that for a distortionless system

Tp( f ) =
2-80
1
(2 f t0) = t0
2 f
Example 2.24: Terminated Lossless Transmission Line

Rs = R0
R0, vp
x(t)
RL = R0
y(t)
1
L
y(t) = x t
2
vp
Lossless transmission line
We conclude that H0 = 1/2 and t0 = L/v p

Note that a real transmission line does have losses that introduces dispersion on a wideband signal
2-81
Example 2.25: Fictitious System

Ampl.
|H(f)|
Radians
1.5
H(f)
1.5
0.5
1
-20
-10
10
-10
10
20
-1.5
Time
Tp(f)
0.015
0.016
0.0125
0.015
0.01
0.014
0.0075
0.013
0.005
0.012
f (Hz)
0.0025
-20
-1
f (Hz)
Time
Tg(f)
-10
f (Hz)
-0.5
0.5
-20
20
10
20
0.011
-20
-10
No distortion on |f | < 10 Hz band
10
20
f (Hz)
Amplitude, phase, group delay, phase delay
The system in this example is artificial, but the definitions can

be observed just the same
For signals with spectral content limited to | f | < 10 Hz there
is no distortion, amplitude or phase/group delay
For 10 < | f | < 15 amplitude distortion is present
For | f | > 15 both amplitude and phase distortion is present
What about the interval 10 < | f | < 15?
2-82
2.7.8
Nonlinear Distortion
In the time domain a nonlinear system may be written as

y(t) =
an x n (t)
n=0
Specifically consider
y(t) = a1 x(t) + a2 x 2(t)
Let
x(t) = A1 cos(1t) + A2 cos(2t)
Expanding the output we have
y(t) = a1 A1 cos(1t) + A2 cos(2t)
2
+ a1 A1 cos(1t) + A2 cos(2t)
= a1 A1 cos(1t) + A2 cos(2t)
a
a2 2
2
2
2
2
+
A +A +
A cos(21t) + A2 cos(22t)
2 1 2
2 1
+ a2 A1 A2 cos[(1 + 2)t] + cos[(1 2)t]

The third line is the desired output
The fourth line is termed harmonic distortion
The fifth line is termed intermodulation distortion
2-83
Input
Output
f1
Input
f1
A2
f2
a2(A1 + A2)
a1a2A1
2f1
f1
a1A1A2
Output
NonLinear
A1
a2A1
NonLinear
0
a1A1
a2A1
A1
a1A1
a2A1
a2A2
2f1
2f2
a1A2 2
0 f2-f1
f1
f2
f1+f2
One and two tones in y(t) = a1 x(t) + a2 x 2 (t) device
In general if y(t) = a1 x(t) + a2 x 2(t) the multiplication theorem implies that

Y ( f ) = a1 X ( f ) + a2 X ( f ) X ( f )
In particular if X ( f ) = A( f /(2W ))
f
Y ( f ) = a1 A
2W
2-84
f
+ a22W A2
2W
Y( f ) =
a 1A
-W
2Wa2A2
+
-2W
2W
a1A + 2Wa2A2
a1A + Wa2A2
Wa2A2
-2W -W
W 2W
Continuous spectrum in y(t) = a1 x(t) + a2 x 2 (t) device
2.7.9
Ideal Filters
1. Lowpass of bandwidth B
f
HLP( f ) = H0
e j2 f t0
2B
|HLP(f)|
H0
-B
slope =
-2t0
-B
HLP(f)
B
2. Highpass with cutoff B
j2 f t0
HHP( f ) = H0 1 ( f /(2B)) e
|HHP(f)|
H0
-B
slope =
-2t0
-B
HHP(f)
B
2-85
3. Bandpass of bandwidth B
HBP( f ) = Hl ( f f 0) + Hl ( f + f 0) e j2 f t0
where Hl ( f ) = H0( f /B)
|HBP(f)|
H0
B
-f0
f0
slope = -2t0
f
HBP(f)
-f0
f0
The impulse response of the lowpass filter is

1
j2 f t0
h LP(t) = F
H0( f /(2B))e
= 2B H0sinc[2B(t t0)]
Ideal filters are not realizable, but simplify calculations are

give useful performance upper bound results
Note that h LP(t) = 0 for t < 0, thus the filter is noncausal
and unrealizable
From the modulation theorem it also follows that
h BP(t) = 2h l (t t0) cos[2 f 0(t t0)]
= 2B H0sinc[B(t t0)] cos[2 f 0(t t0)]
2-86
hLP(t)
hBP(t)
2BH0
t0 - 1
2B
t0
2BH0
t0
t
t0 + 1
2B
t
t0 - 1
2B
t0 + 1
2B
Ideal lowpass and bandpass impulse responses
2.7.10
Realizable Filters
We can approximate ideal filters with realizable filters such as

Butterworth, Chebyshev, and Bessel, to name a few
We will only consider the lowpass case since via frequency
transformations we can obtain the others
Butterworth
A Butterworth filter has a maximally flat (flat in the sense of
derivatives of the amplitude response at dc being zero) passband
In the s-domain (s = + j) the transfer function of a lowpass
design is
where
cn
HBU(s) =
(s s1)(s s2) (s sn )

1 2k 1
sk = c exp
+
, k = 1, 2, . . . , n
2
2n
2-87
Note that the poles are located on a semi-circle of radius c =

2 f c , where f c is the 3dB cuttoff frequency of the filter
The amplitude response of a Butterworth filter is simply
1
|HBU( f )|
1 + ( f / f c )2n
Butterworth n = 4 lowpass filter
Chebyshev
A Chebyshev type I filter (ripple in the passband), is is designed to maintain the maximum allowable attenuation in the
passband yet have maximum stopband attenuation
The amplitude response is given by
|HC( f )| =
where
Cn ( f ) =
2-88
1 + 2Cn2( f )
cos(n cos1( f / f c )),

cosh(n cosh1( f / f c )),
0 | f | fc
| f | > fc
The poles are located on an ellipse as shown below
Chebyshev n = 4 lowpass filter
Bessel
A Bessel filter is designed to maintain linear phase in the passband at the expense of the amplitude response
HBE( f ) =
Kn
Bn ( f )
where Bn ( f ) is a Bessel polynomial of order n (see text) and

K n is chosen so that the filter gain is unity at f = 0
2-89
Amplitude Rolloff and Group Delay Comparision

Compare Butterworth, 0.1 dB ripple Chebyshev, and Bessel
n = 3 Amplitude response
2-90
n = 3 Group delay
Filter Construction Techniques

Construction
Type
LC (passive)
Active
Crystal
Ceramic
Surface acoustic
waves (SAW)
Transmission line
Cavity
2.7.11
Description of El- Center Freements or Filter

quency Range
lumped elements
DC300 MHz
or higher in integrated form
R, C, op-amps
DC500 kHz
or higher using
WB op-amps
quartz crystal
1kHz 100
MHz
ceramic disks with 10kHz 10.7
electrodes
MHz
interdigitated fin- 10-800 MHz,
gers on a Piezoelectric substrate
quarterwave stubs, UHF and miopen and short ckt crowave
machined
and Microwave
plated metal
Unloaded
(typical
100
Filter Application
Audio, video,
IF and RF
200
Audio and low

RF
100,000
IF
1,000
IF
variable
IF and RF
1,000
RF
10,000
RF
Pulse Resolution, Risetime, and Bandwidth
Problem: Given a non-bandlimited signal, what is a reasonable estimate of the signals transmission bandwidth?
We would like to obtain a relationship to the signals time duration
Step 1: We first consider a time domain relationship by seeking
a constant T such that
T x(0) =
|x(t)| dt
Make areas
equal via T
x(0)
|x(t)|
-T/2
T/2
2-91
Note that

x(t) dt =
and
which implies
x(t)e j2 f t dt
|x(t)| dt
f =0
= X (0)
x(t) dt
T x(0) X (0)
Step 2: Find a constant W such that
2W X (0) =
Note that

and
Make areas
equal via W
|X ( f )| d f
X(0)
|X(f)|
-W
X( f )d f =
which implies that
j2 f t
X ( f )e
d f
|X ( f )| d f
t=0
= x(0)
X( f )d f
2W X (0) x(0)
2-92
Combining the results of Step 1 and Step 2, we have

2W X (0) x(0)
1
X (0)
T
1
T
1
2T
or
2W
or
Example 2.26: Rectangle Pulse

Consider the pulse x(t) = (t/T )
We know that X ( f ) = T sinc( f T )
x(t)
-1
|X(f)|/T
-0.5
0.8
0.8
0.6
0.6
0.4
0.4
0.2
0.2
0.5
t/T
-3
-2
-1
Lower
bound for
W
-1/(2T) 1/(2T)
fT
f
Pulse width versus Bandwidth, is W 1/(2T ?
We see that for the case of the sinc( ) function the bandwidth,
W , is clearly greater than the simple bound predicts
2-93
Risetime
There is also a relationship between the risetime of a pulse-like
signal and bandwidth
Definition: The risetime, TR , is the time required for the leading edge of a pulse to go from 10% to 90% of its final value
Given the impulse response h(t) for an LTI system, the step
response is just

ys (t) =
h()u(t ) d
t
t
if causal
=
h() d =
h() d
0
Example 2.27: Risetime of RC Lowpass

The RC lowpass filter has impulse response
h(t) =
1 t/(RC)
e
u(t)
RC
The step response is
t/(RC)
ys (t) = 1 e
u(t)
2-94
The risetime can be obtained by setting ys (t1) = 0.1 and ys (t2) =

0.9
t1
0.1 = 1 et1/(RC) ln(0.9) =
RC
t
2
0.9 = 1 et2/(RC) ln(0.1) =
RC
The difference t2 t1 is the risetime

TR = t2 t1 = RC ln(0.9/0.1) 2.2RC =
0.35
f3
where f 3 is the RC lowpass 3dB frequency
Example 2.28: Risetime of Ideal Lowpass

The risetime of an ideal lowpass filter is of interest since it is
used in modeling and also to see what an ideal filter does to a
step input
The impulse response is

f
h(t) = F 1
= 2Bsinc[2Bt]
2B
The step response then is
t
ys =
2Bsinc[2B] d
1 2 Bt sin u
=
du

u
1 1
= + Si[2 Bt]
2
where Si( ) is a special function known as the sine integral
We can numerically find the risetime to be
TR
0.44
B
2-95
Step Response of RC Lowpass
Step Response of Ideal Lowpass

1
0.8
0.6
0.4
0.8
0.6
2.2
0.4
0.2
0.44
0.2
1
t RC
-2
-1
t/B
RC and ideal lowpass risetime comparison
2-96
2.8. SAMPLING THEORY
2.8
Sampling Theory
Integrate with Chapter 3 material.
2.9
The Hilbert Transform
Integrate with Chapter 3 material.
2.10
The Discrete Fourier Transform and

FFT
2-97
2-98
Chapter
Analog Modulation
Contents
3.1
3.2
3.3
3.4
Linear Modulation . . . . . . . . . . . . . . . . . . . .
3-3
3.1.1
Double-Sideband Modulation (DSB) . . . . . .
3-3
3.1.2
Amplitude Modulation . . . . . . . . . . . . . .
3-8
3.1.3
Single-Sideband Modulation . . . . . . . . . . . 3-21
3.1.4
Vestigial-Sideband Modulation . . . . . . . . . . 3-35
3.1.5
Frequency Translation and Mixing . . . . . . . . 3-38
Angle Modulation . . . . . . . . . . . . . . . . . . . . 3-46

3.2.1
Narrowband Angle Modulation . . . . . . . . . 3-48
3.2.2
Spectrum of an Angle-Modulated Signal . . . . 3-50
3.2.3
Power in an Angle-Modulated Signal . . . . . . 3-56
3.2.4
Bandwidth of Angle-Modulated Signals . . . . . 3-56
3.2.5
Narrowband-to-Wideband Conversion . . . . . . 3-63
3.2.6
Demodulation of Angle-Modulated Signals . . . 3-63
Interference . . . . . . . . . . . . . . . . . . . . . . . 3-73
3.3.1
Interference in Linear Modulation . . . . . . . . 3-74
3.3.2
Interference in Angle Modulation . . . . . . . . 3-76
Feedback Demodulators . . . . . . . . . . . . . . . . . 3-81
3-1
CHAPTER 3. ANALOG MODULATION
Phase-Locked Loops for FM Demodulation . . . 3-81
3.4.2
PLL Frequency Synthesizers . . . . . . . . . . . 3-100
3.4.3
Frequency-Compressive Feedback . . . . . . . . 3-104
3.4.4
Coherent Carrier Recovery for DSB Demodulation 3-106
3.5
Sampling Theory . . . . . . . . . . . . . . . . . . . . . 3-110
3.6
Analog Pulse Modulation . . . . . . . . . . . . . . . . 3-115
3.7
3.8
3.9
3-2
3.4.1
3.6.1
Pulse-Amplitude Modulation (PAM) . . . . . . . 3-115
3.6.2
Pulse-Width Modulation (PWM) . . . . . . . . . 3-117
3.6.3
Pulse-Position Modulation . . . . . . . . . . . . 3-117
Delta Modulation and PCM . . . . . . . . . . . . . . . 3-118

3.7.1
Delta Modulation (DM) . . . . . . . . . . . . . 3-118
3.7.2
Pulse-Code Modulation (PCM) . . . . . . . . . 3-121
Multiplexing . . . . . . . . . . . . . . . . . . . . . . . 3-124
3.8.1
Frequency-Division Multiplexing (FDM) . . . . 3-125
3.8.2
Quadrature Multiplexing (QM) . . . . . . . . . . 3-128
3.8.3
Time-Division Multiplexing (TDM) . . . . . . . 3-129
General Performance of Modulation Systems in Noise
3-133
3.1. LINEAR MODULATION
We are typically interested in locating a message signal to some

new frequency location, where it can be efficiently transmitted
The carrier of the message signal is usually sinusoidal
A modulated carrier can be represented as
xc (t) = A(t) cos 2 f c t + (t)
where A(t) is linear modulation, f c the carrier frequency, and

(t) is phase modulation
3.1
Linear Modulation
For linear modulation schemes, we may set (t) = 0 without

loss of generality
xc (t) = A(t) cos(2 f c t)
with A(t) placed in one-to-one correspondence with the message signal
3.1.1
Double-Sideband Modulation (DSB)
Let A(t) m(t), the message signal, thus

xc (t) = Ac m(t) cos(2 f c t)
From the modulation theorem it follows that
X c( f ) =
1
1
Ac M( f f c ) + Ac M( f + f c )
2
2
3-3
carrier filled envelope
xc(t)
m(t)
DSB time domain waveforms

M(f)
M(0)
f
Xc(f)
1
A M(0)
2 c
LSB
-fc
USB
fc
DSB spectra
Coherent Demodulation
The received signal is multiplied by the signal 2 cos(2 f c t),
which is synchronous with the transmitter carrier
m(t)
xc(t)
xr(t)
Accos[2fct]
Modulator
3-4
d(t)
LPF
yD(t)
2cos[2fct]
Channel
Demodulator
For an ideal channel xr (t) = xc (t), so
d(t) = Ac m(t) cos(2 f c t) 2 cos(2 f c t)

= Ac m(t) + Ac m(t) cos(2(2 f c )t)
where we have used the trig identity 2 cos2 x = 1 + cos 2x
The waveform and spectra of d(t) is shown below (assuming

m(t) has a triangular spectrum in D( f ))
d(t)
Lowpass filtering will remove the

double frequency carrier term
D(f)
AcM(0)
1
A M(0)
2 c
-W
-2fc
Lowpass
modulation
recovery filter
1
A M(0)
2 c
2fc
Waveform and spectrum of d(t)
Typically the carrier frequency is much greater than the message bandwidth W , so m(t) can be recovered via lowpass filtering
The scale factor Ac can be dealt with in downstream signal
processing, e.g., an automatic gain control (AGC) amplifier
3-5
Assuming an ideal lowpass filter, the only requirement is that

the cutoff frequency be greater than W and less than 2 f c W
The difficulty with this demodulator is the need for a coherent
carrier reference
To see how critical this is to demodulation of m(t) suppose that
the reference signal is of the form
c(t) = 2 cos[2 f c t + (t)]
where (t) is a time-varying phase error
With the imperfect carrier reference signal
d(t) = Ac m(t) cos (t) + Ac m(t) cos[2 f c t + (t)]
y D (t) = m(t) cos (t)
Suppose that (t) is a constant or slowly varying, then the
cos (t) appears as a fixed or time varying attenuation factor
Even a slowly varying attenuation can be very detrimental from
a distortion standpoint
If say (t) = f t and m(t) = cos(2 f m t), then
y D (t) =
1
[cos[2( f m f )t] + cos[2( f m + f )t]]
2
which is the sum of two tones

Being able to generate a coherent local reference is also a practical manner
3-6
One scheme is to simply square the received DSB signal

xr2(t) = A2c m 2(t) cos2(2 f c t)
1
1
= A2c m 2(t) + A2c m 2(t) cos[2(2 f c )t]
2
2
xr(t)
LPF
xr(t)
yD(t)
( )2
BPF
very narrow
(tracking) bandpass filter
divide
by 2
Acos2fct
Carrier recovery concept using signal squaring
Spectrum
of m2(t)
Assuming that m 2(t) has a nonzero DC value, then the double

frequency term will have a spectral line at 2 f c which can be
divided by two following filtering by a narrowband bandpass
filter, i.e., F{m 2(t)} = k( f ) +
Filter this component
for coherent demod
2fc
Note that unless m(t) has a DC component, X c ( f ) will not

contain a carrier term (read ( f f c ), thus DSB is also called
a suppressed carrier scheme
3-7
Consider transmitting a small amount of unmodulated carrier

xc(t)
m(t)
k << 1
k
Accos2fct
use a narrowband filter

(phase-locked loop) to extract
the carrier in the demod.
AcM(0)/2
-fc
3.1.2
fc
Amplitude Modulation
Amplitude modulation (AM) can be created by simply adding

a DC bias to the message signal
xc (t) = A + m(t) Ac cos(2 f c t)
= Ac 1 + am n (t) cos(2 f c t)
where Ac = A Ac , m n (t) is the normalized message such that

min m n (t) = 1,
m n (t) =
m(t)
| min m(t)|
and a is the modulation index

a=
3-8
| min m(t)|
A
xc(t)
Ac(1 - a)
A + max m(t)
A + min m(t)
a<1
t
Note that the envelope does not cross

zero in the case of
AM having a < 1
A + m(t)
m(t)
Bias term
xc(t)
Accos[2fct]
Generation of AM and a sample wavefrom
Note that if m(t) is symmetrical about zero and we define d1 as

the peak-to-peak value of xc (t) and d2 as the valley-to-valley
value of xc (t), it follows that
a=
d1 d2
d1 + d2
proof: max m(t) = min m(t) = | min m(t)|, so

d1 d2
2[(A + | min m(t)|) (A | min m(t)|)]
=
d1 + d2
2[(A + | min m(t)|) + (A | min m(t)|)]
| min m(t)|
=
=a
A
3-9
The message signal can be recovered from xc (t) using a technique known as envelope detection
A diode, resistor, and capacitor is all that is needed to construct
and envelope detector
eo(t)
xr(t)
Recovered envelope
with proper RC
selection
eo(t)
t
The carrier is removed if 1/fc << RC << 1/W
Envelope detector
The circuit shown above is actually a combination of a nonlinearity and filter (system with memory)
A detailed analysis of this circuit is more difficult than you
might think
A SPICE circuit simulation is relatively straight forward, but it
can be time consuming if W f c
3-10
The simple envelope detector fails if Ac [1 + am n (t)] < 0

In the circuit shown above, the diode is not ideal and
hence there is a turn-on voltage which further limits the
maximum value of a
The RC time constant cutoff frequency must lie between both
W and f c , hence good operation also requires that f c W
3-11
Digital signal processing based envelope detectors are also possible

Historically the envelope detector has provided a very low-cost
means to recover the message signal on AM carrier
The spectrum of an AM signal is
X c( f ) =
Ac
( f f c ) + ( f + f c )
2
pure carrier spectrum
a Ac
+
Mn ( f f c ) + Mn ( f + f c )
2
DSB spectrum
AM Power Efficiency
Low-cost and easy to implement demodulators is a plus for

AM, but what is the downside?
Adding the bias term to m(t) means that a fraction of the total
transmitted power is dedicated to a pure carrier
The total power in xc (t) is can be written in terms of the time
average operator introduced in Chapter 2
xc2(t) = A2c [1 + am n (t)]2 cos2(2 f c t)
A2c
=
[1 + 2am n (t) + a 2m 2n (t)][1 + cos(2(2 f c )t]
2
If m(t) is slowly varying with respect to cos(2 f c t), i.e.,
m(t) cos c t 0,
3-12
then
xc2(t)
A2c
=
1 + 2am n (t) + a 2m 2n (t)
2
A2c
A2c
a 2 A2c 2
2
2
=
1 + a m (t) =
+
m n (t)
2
2
2

Pcarrier
Psidebands
where the last line resulted from the assumption m(t) = 0

(the DC or average value of m(t) is zero)
Definition: AM Efficiency
Eff
a 2m 2n (t) also
m 2(t)
=
= 2
1 + a 2m 2n (t)
A + m 2(t)
Example 3.1: Single Sinusoid AM

An AM signal of the form
xc (t) = Ac [1 + a cos(2 f m t + /3)] cos(2 f c t)
contains a total power of 1000 W
The modulation index is 0.8
Find the power contained in the carrier and the sidebands, also
find the efficiency
The total power is
1000 =
xc2(t)
A2c a 2 A2c
=
+
m 2n (t)
2
2
3-13
It should be clear that in this problem m n (t) = cos(2 f m t), so

m 2n (t) = 1/2 and
1
1
33 2
1000 = A2c
+ 0.64 =
A
2 4
50 c
Thus we see that
A2c = 1000
and
Pcarrier =
50
= 1515.15
33
1 2 1515
A =
= 757.6 W
2 c
2
and thus
Psidebands = 1000 Pc = 242.4 W
The efficiency is
Eff =
242.4
= 0.242 or 24.2%
1000
The magnitude and phase spectra can be plotted by first expanding out xc (t)
xc (t) = Ac cos(2 f c t) + a Ac cos(2 f m t + /3) cos(2 f c t)
= Ac cos(2 f c t)
a Ac
+
cos[2( f c + f m )t + /3]
2
a Ac
+
cos[2( f c f m )t /3]
2
3-14
|Xc(f)|
Ac/2
0.8Ac/4
0
-fc
Xc(f)
0
fc-fm fc fc+fm
/3
f
-/3
Amplitude and phase spectra for one tone AM
Example 3.2: Pulse Train with DC Offset

m(t)
2
t
-1
Tm/3
Tm
Find m n (t) and the efficiency E

From the definition of m n (t)
m n (t) =
The efficiency is
m(t)
m(t)
=
= m(t)
| min m(t)| | 1|
a 2m 2n (t)
E=
1 + a 2m 2n (t)
3-15
To obtain m 2n (t) we form the time average

Tm /3
Tm
1
m 2n (t) =
(2)2 dt +
(1)2 dt
Tm 0
Tm /3
1 Tm
2Tm
4 2 7
=
4+
1 = + =
Tm 3
3
3 3 3
thus
(7/3)a 2
7a 2
E=
=
1 + (7/3)a 2
3 + 7a 2
The best AM efficiency we can achieve with this waveform is

when a = 1
Eff
=
= 0.7 or 70%
a=1
10
Suppose that the message signal is m(t) as given here
Now min m(t) = 2 and m n (t) = m(t)/2 and
m 2n (t) =
1
2
1
(1)2 + (1/2)2 =
3
3
2
The efficiency in this case is

Eff
a2
(1/2)a 2
=
=
1 + (1/2)a 2
2 + a2
Now when a = 1 we have E f f = 1/3 or just 33.3%

Note that for 50% duty cycle squarewave the efficiency maximum is just 50%
3-16
Example 3.3: Multiple Sinusoids

Suppose that m(t) is a sum of multiple sinusoids (multi-tone
AM)
M
m(t) =
Ak cos(2 f k t + k )
k=1
where M is the number of sinusoids, f k values might be constrained over some band of frequencies W , e.g., f k W , and
the phase values k can be any value on [0, 2 ]
To find m n (t) we need to find min m(t)

M
A lower bound on min m(t) is k=1
Ak ; why?
The worst case value may not occur in practice depending upon
the phase and frequency values, so we may have to resort to a
numerical search or a plot of the waveform
Suppose that M = 3 with f k = {65, 100, 35} Hz, Ak =
{2, 3.5, 4.2}, and k = {0, /3, /4} rad.
>> [m,t] = M_sinusoids(1000,[65 100 35],[2 3.5 4.2],...
[0 pi/3 -pi/4], 20000);>> plot(t,m)
>> min(m)
ans =
-7.2462e+00
>> -sum([2 3.5 4.2]) % worst case minimum value

ans =
-9.7000e+00
>> subplot(311)
>> plot(t,(1 + 0.25*m/abs(min(m))).*cos(2*pi*1000*t))
>> hold
3-17
Current plot held

>> plot(t,1 + 0.25*m/abs(min(m)),r)
>> subplot(312)
>> hold
Current plot held
>> subplot(313)
>> hold
Current plot held
8
6
m(t) Amplitude
4
2
0
2
4
6
8
min m(t)
0
0.005
0.01
0.015
0.02
0.025 0.03
Time (s)
0.035
0.04
0.045
0.05
Finding min m(t) graphically
The normalization factor is approximately given by 7.246, that

is
m(t)
m n (t) =
7.246
Shown below are plots of xc (t) for a = 0.25, 0.5 and 1 using
f c = 1000 Hz
3-18
xc(t), a = 1.0
xc(t), a = 0.5
xc(t), a = 0.25
2
0
2
2
0.005
0.01
0.015
0.02
0.025
0.03
0.035
0.04
0.045
0.05
0.005
0.01
0.015
0.02
0.025
0.03
0.035
0.04
0.045
0.05
0.005
0.01
0.015
0.02
0.025 0.03
Time (s)
0.035
0.04
0.045
0.05
0
2
2
0
2
Modulation index comparison ( f c = 1000 Hz)
To obtain the efficiency of multi-tone AM we first calculate

m 2n (t) assuming unique frequencies
m 2n (t)
k=1
2
A2k
2| min m(t)|2
2 + 3.52 + 4.22
=
= 0.3227
2 7.2462
The maximum efficiency is just
Eff
a=1
0.3227
= 0.244 or 24.4%
1 + 0.3227
3-19
A remaining interest is the spectrum of xc (t)
Ac
( f f c ) + ( f + f c )
2
M
a Ac jk
+
Ak e ( f ( f c + f k ))
4 k=1
jk
+e
( f + ( f c + f k )) (USB terms)
X c( f ) =
a Ac jk
+
Ak e ( f ( f c f k ))
4 k=1
jk
+e
( f + ( f c f k )) (LSB terms)
0.5
Amplitude Spectra (|Xc(f)|)
0.45
0.4
Carrier with
Ac = 1
0.35
0.3
0.25
0.2
0.15
0.1
Sidebands for
a = 0.5
0.05
0
1000 800 600 400 200

0
200
Frequency (Hz)
400
600
800 1000
Amplitude spectra
3-20
3.1.3
Single-Sideband Modulation
In the study of DSB it was observed that the USB and LSB
spectra are related, that is the magnitude spectra about f c has
even symmetry and phase spectra about f c has odd symmetry
The information is redundant, meaning that m(t) can be reconstructed one or the other sidebands
Transmitting just the USB or LSB results in single-sideband
(SSB)
For m(t) having lowpass bandwidth of W the bandwidth required for DSB, centered on f c is 2W
Since SSB operates by transmitting just one sideband, the transmission bandwidth is reduced to just W
XDSB(f)
M(f)
XSSB(f)
XSSB(f)
LSB
fc - W
USB
removed
fc
fc - W
fc
f
fc+W
USB
LSB
removed
fc
f
fc+W
DSB to two forms of SSB: USSB and LSSB
The filtering required to obtain an SSB is best explained with

the aid of the Hilbert transform, so we divert from text Chapter
3-21
3 back to Chapter 2 to briefly study the basic properties of this

transform
Hilbert Transform
The Hilbert transform is nothing more than a filter that shifts
the phase of all frequency components by /2, i.e.,
H ( f ) = jsgn( f )
where
sgn( f ) =
1,
0,
1,
f >0
f =0
f <0
The Hilbert transform of signal x(t) can be written in terms of

the Fourier transform and inverse Fourier transform
x(t)
= F 1 jsgn( f )X ( f )
= h(t) x(t)
where h(t) = F 1{H ( f )}
We can find the impulse response h(t) using the duality theorem and the differentiation theorem
d
F
H ( f ) ( j2t)h(t)
df
where here H ( f ) = jsgn( f ), so
d
H ( f ) = 2 j( f )
df
3-22
Clearly,
so
F 1{2 j( f )} = 2 j
h(t) =
and
2 j
1
=
j2 t
t
1 F
jsgn( f )
t
In the time domain the Hilbert transform is the convolution

integral

x()
x(t )
x(t)
=
d =
d
(t
Note that since the Hilbert transform of x(t) is a /2 phase

shift, the Hilbert transform of x(t)
is
= x(t)
x(t)
why? observe that ( jsgn( f ))2 = 1
Example 3.4: x(t) = cos 0t

By definition
1
X ( f ) = jsgn( f ) ( f f 0) + ( f + f 0)
2
1
1
= j ( f f c ) + j ( f + f 0)
2
2
3-23
so from e j0t = ( f f 0)
1
1
x(t)
= j e j0t + j e j0t
2
2
j0 t
j0 t
e
e
=
= sin 0t
2j
or
It also follows that
cos
0t = sin 0t
sin
0t = cos
0t = cos 0t
= x(t)
since x(t)
Hilbert Transform Properties

1. The energy (power) in x(t) and x(t)
are equal
The proof follows from the fact that |Y ( f )|2 = |H ( f )|2|X ( f )|

and | jsgn( f )|2 = 1
2. x(t) and x(t)

are orthogonal, that is

x(t)x(t)
dt = 0 (energy signal)
T
1
lim
x(t)x(t)
dt = 0 (power signal)
T 2T T
3-24
The proof follows for the case of energy signals by generalizing Parsevals theorem

x(t)x(t)
dt =
X ( f ) X ( f ) d f
=
( jsgn( f )) |X ( f )|2 d f = 0

odd
even
3. Given signals m(t) and c(t) such that the corresponding spectra are
M( f ) = 0 for | f | > W (a lowpass signal)
C( f ) = 0 for | f | < W (c(t) a highpass signal)
then
= m(t)c(t)
m(t)c(t)
Example 3.5: c(t) = cos 0t
Suppose that M( f ) = 0 for | f | > W and f 0 > W then
m(t)
cos 0t = m(t)cos
0 t
= m(t) sin 0t
Analytic Signals
Define analytic signal z(t) as
z(t) = x(t) + j x(t)
where x(t) is a real signal

3-25
The envelope of z(t) is |z(t)| and is related to the envelope

discussed with DSB and AM signals
The spectrum of an analytic signal have single-sideband characteristics
In particular for z p (t) = x(t) + j x(t)
Z p ( f ) = X ( f ) + j jsgn( f )X ( f )
= X ( f ) 1 + sgn( f )
2X ( f ), f > 0
=
0,
f <0
Note: Only positive frequencies present
Similarly for z n (t) = x(t) j x(t)
Z n ( f ) = X ( f ) 1 sgn( f )
0,
f >0
=
2X ( f ), f < 0
3-26
X(f)
-W
Zp(f)
-W
Zn(f)
-W
The spectra of analytic signals can suppress positive or negative

frequencies
Return to SSB Development

xDSB(t)
m(t)
Sideband
Filter
xSSB(t)
LSB or USB
Accosct
Basic SSB signal generation
In simple terms, we create an SSB signal from a DSB signal

using a sideband filter
The mathematical representation of LSSB and USSB signals
makes use of Hilbert transform concepts and analytic signals
3-27
DSB Signal Starting Point
-fc
Formation of HL(f)
+1/2
sgn(f + fc)/2
fc
f
-1/2
+1/2
-sgn(f - fc)/2
f
-1/2
HL(f) = [sgn(f + fc) - sgn(f - fc)]/2
-fc
fc
An ideal LSSB filter
From the frequency domain expression for the LSSB, we can

ultimately obtain an expression for the LSSB signal, xcLSSB (t),
in the time domain
Start with X DSB( f ) and the filter HL ( f )
X cLSSB ( f ) =
3-28
1
Ac M( f + f c ) + M( f f c )
2
1
sgn( f + f c ) sgn( f f c )
2
1
Ac M( f + f c )sgn( f + f c )
4
+ M( f f c )sgn( f f c )
1
Ac M( f + f c )sgn( f f c )
4
+ M( f f c )sgn( f f c )
1
= Ac M( f + f c ) + M( f f c )
4
1
+ Ac M( f + f c )sgn( f + f c )
4
M( f f c )sgn( f f c )
X cLSSB ( f ) =
The inverse Fourier transform of the first term is DSB, i.e.,
1
1
F
Ac m(t) cos c t Ac M( f + f c ) + M( f f c )
2
4
The second term can be inverse transformed using

F
m(t)
jsgn( f ) M( f )
so
jc t
F 1 M( f + f c )sgn( f + f c ) = j m(t)e
since m(t)e jc t M( f f c )
Thus
1
Ac F 1 M( f + f c )sgn( f + f c ) M( f f c )sgn( f f c )
4
1
1
jc t
jc t
=
Ac j m(t)e
j m(t)e
=
m(t)
sin c t
4
2
3-29
Finally,
xcLSSB (t) =
1
1
Ac m(t) cos c t + Ac m(t)
sin c t
2
2
Similarly for USSB it can be shown that

xcUSSB (t) =
1
1
Ac m(t) cos c t Ac m(t)
sin c t
2
2
The direct implementation of SSB is very difficult due to the

requirements of the filter
By moving the phase shift frequency from f c down to DC (0
Hz) the implementation is much more reasonable (this applies
to a DSP implementation as well)
The phase shift is not perfect at low frequencies, so the modulation must not contain critical information at these frequencies
cosct
m(t)
H(f) =
-jsgn(f)
sinct
-90
Carrier Osc.
cosct
+
xc(t)
+
-
LSB
USB
Phase shift modulator for SSB
3-30
Demodulation
The coherent demodulator first discussed for DSB, also works
for SSB
d(t)
xr(t)
yD(t)
LPF
4cos[2fct + (t)]
1/Ac scale factor

included
Coherent demod for SSB
Carrying out the analysis to d(t), first we have
1
d(t) = Ac m(t) cos c t m(t)
sin c t 4 cos(c t + (t))
2
= Ac m(t) cos (t) + Ac m(t) cos[2c t + (t)]
Ac m(t)
sin (t) Ac m(t)
sin[2c t + (t)]
so
y D (t) = m(t) cos (t) m(t)

sin (t)
(t) small
m(t) m(t)(t)
The m(t)
sin (t) term represents crosstalk
Another approach to demodulation is to use carrier reinsertion
and envelope detection
e(t)
xr(t)
Envelope
Detector
yD(t)
Kcosct
3-31
e(t) = xr (t) + K cos c t
1
1
=
Ac m(t) + K cos c t Ac m(t)
sin c t
2
2
To proceed with the analysis we must find the envelope of e(t),
which will be the final output y D (t)
Finding the envelope is a more general problem which will be
useful in future problem solving, so first consider the envelope
of
x(t) = a(t) cos c t b(t) sin c t
inphase
quadrature
jc t
jc t
= Re a(t)e
+ jb(t)e
= Re [a(t) + jb(t)] e jc t
R(t)=complex
envelope
In a phasor diagram x(t) consists of an inphase or direct component and a quadrature component
Quadrature - Q
Note: R(t) =
b(t)
R(t)
(t)
a(t)
3-32
R(t)ej(t) = a(t) + jb(t)
In-phase - I
where the resultant R(t) is such that

a(t) = R(t) cos (t)
b(t) = R(t) sin (t)
which implies that
x(t) = R(t) cos (t) cos c t sin (t) sin c t
= R(t) cos c t + (t)
where (t) = tan1[b(t)/a(t)]
The signal envelope is thus given by
R(t) = a 2(t) + b2(t)
The output of an envelope detector will be R(t) if a(t) and b(t)

are slowly varying with respect to cos c t
In the SSB demodulator
2
2
1
1
y D (t) =
Ac m(t) + K +
Ac m(t)
2
2
2
If we choose k such that (Ac m(t)/2 + K )2 (Ac m(t)/2)
,
then
1
y D (t) Ac m(t) + K
2
Note:
The above analysis assumed a phase coherent reference
In speech systems the frequency and phase can be adjusted to obtain intelligibility, but not so in data systems
3-33
The approximation relies on the binomial expansion

1
(1 + x)1/2 1 + x for |x| 1
2
Example 3.6: Noncoherent Carrier Reinsertion

Let m(t) = cos m t, m c and the reinserted carrier be
K cos[(c + )t]
Following carrier reinsertion we have
1
Ac cos m t cos c t
2
1
Ac sin c t sin c t + K cos (c + )t
2
1
= Ac cos (c m )t + K cos (c + )t
2
e(t) =
We can write e(t) as the real part of a complex envelope times

a carrier at either c or c +
In this case, since K will be large compared to Ac /2, we write
1
jm t jc t
e(t) = Ac Re e
e
2
j (c +)t
+ K Re 1 e
1
j (m )t
j (c +)t
= Re
Ac e
+K e
2
complex envelope R(t)
3-34
Finally expanding the complex envelope into the real and imaginary parts we can find the real envelope R(t)
y D (t) =
Ac cos[m + )t] + K
2
1
21/2
+
Ac sin[(m + )t]
2
1
Ac cos[(m )t] + K
2
where the last line follows for K Ac

Note that the frequency error causes the recovered message signal to shift up or down in frequency by , but not
both at the same time as in DSB, thus the recovered speech
signal is more intelligible
3.1.4
Vestigial-Sideband Modulation
Vestigial sideband (VSB) is derived by filtering DSB such that

one sideband is passed completely while only a vestige remains
of the other
Why VSB?
1. Simplifies the filter design
2. Improves the low-frequency response and allows DC to
pass undistorted
3. Has bandwidth efficiency advantages over DSB or AM,
similar to that of SSB
3-35
A primary application of VSB is the video portion of analog

television (note HDTV is replacing this in the US)
The generation of VSB starts with DSB followed by a filter
that has a 2 transition band, e.g.,
f < Fc
0,
|H ( f )| = f (2fc ) , f c f f c +
1,
f > f +
c
|H(f)|
fc
fc -
fc +
Ideal VSB transmitter filter amplitude response
VSB can be demodulated using a coherent demod or using carrier reinsertion and envelope detection
Transmitted Two-Tone Spectrum
(only single-sided shown)
A(1 - )/2
B/2
A/2
0
f - f2
f - f1
fc
f + f1
f + f2
Two-tone VSB signal

3-36
Suppose the message signal consists of two tones

m(t) = A cos 1t + B cos 2t
Following the DSB modulation and VSB shaping,
xc (t) =
1
A cos(c 1)t
2
1
1
+ A(1 ) cos(c + 1)t + B cos(c + 2)t
2
2
A coherent demod multiplies the received signal by 4 cos c t

to produce
e(t) = A cos 1t + A(1 ) cos 1t + B cos 2t
= A cos 1t + B cos 2t
which is the original message signal
The symmetry of the VSB shaping filter has made this possible
In the case of broadcast TV the carrier in included at the transmitter to insure phase coherency and easy demodulation at the
TV receiver (VSB + Carrier)
Very large video carrier power is required for typical TV
station, i.e., greater than 100,000 W
To make matters easier still, the precise VSB filtering is
not performed at the transmitter due to the high power
requirements, instead the TV receiver does this
3-37
Transmitter
Output
Video Carrier
Audio Carrier
0
-1.75 -0.75
2 interval
Receiver
Shaping
Filter
4.0 4.5 4.75
(f - fcv) MHz
1
-0.75
0.75
4.0
4.75
(f - fcv) MHz
Broadcast TV transmitter spectrum and receiver shaping filter
3.1.5
Frequency Translation and Mixing
Used to translate baseband or bandpass signals to some new

center frequency
m(t)cos1t
f1
e(t)
f
BPF
at
f2
f2
Local oscillator of the form
Frequency translation system
Assuming the input signal is DSB of bandwidth 2W the mixer

(multiplier) output is
local osc (LO)
e(t) = m(t) cos(1t) 2 cos(1 2)t

= m(t) cos(2t) + m(t) cos[(21 2)t]
3-38
The bandpass filter bandwidth needs to be at least 2W Hz wide

Note that if an input of the form k(t) cos[(1 22)t] is present
it will be converted to 2 also, i.e.,
e(t) = k(t) cos(2t) + k(t) cos[(21 32)t],
and the bandpass filter output is k(t) cos(2t)
The frequencies 1 22 are the image frequencies of 1 with
respect to LO = 1 2
Example 3.7: AM Broadcast Superheterodyne Receiver
Tunable
RF-Amp
Joint tuning
IF Filt/
Amp
Local
Osc.
fIF
Env
Det
Automatic gain
control
Audio
Amp
For AM BT = 2W
AM Broadcast Specs: fc = 540 to 1600 kHz on 10 kHz spacings

carrier stability
Modulated audio flat 100 Hz to 5 kHz
Typical fIF = 455 kHz
AM Superheterodyne receiver
We have two choices for the local oscillator, high-side or lowside tuning
3-39
Low-side: 540455 f LO 1600455 or 85 f LO

1145, all frequencies in kHz
High-side: 540 + 455 f LO 1600 + 455 or 995
f LO 2055, all frequencies in kHz
The high-side option is advantageous since the tunable oscillator or frequency synthesizer has the smallest frequency ratio
f LO,max/ f LO,min = 2055/995 = 2.15
Suppose the desired station is at 560 kHz, then with high-side
tuning we have f LO = 560 + 455 = 1015 kHz
The image frequency is at f image = f c + 2 f IF = 560 + 2
455 = 1470 kHz (note this is another AM radio station center
frequency
Desired
BRF
Input
455
560
fLO
Mixer
Output
BIF
Image
Out of
mixer
1015-560
IF BPF
This is removed
with RF BPF
Potential Image
fIF
fIF
1015
(560+455)
1470
1470
1575
(560+1015)
f (kHz)
f (kHz)
f (kHz)
f (kHz)
2485
(1470+1015)
455
0 1470-1015
Receiver frequency plan including images
3-40
Example 3.8: A Double-Conversion Receiver

fc = 162.475 MHz
(WX #4)
10.7 MHz &

335.65 MHz
Tunable
RF-Amp
455 kHz &

21.855 MHz
455 kHz
IF BPF
10.7 MHz
IF BPF
1st
LO
fLO1 = 173.175 MHz
FM
Demod
2nd
LO
fLO2 = 11.155 MHz
Double-conversion superheterodyne receiver
Consider a frequency modulation (FM) receiver that uses doubleconversion to receive a signal con carrier frequency 162.475
MHz (weather channel #4)
Frequency modulation will be discussed in the next section
The dual-conversion allows good image rejection by using a
10.7 MHz first IF and then can provide good selectivity by
using a second IF at 455 kHz; why?
The ratio of bandwidth to center frequency can only be so
small in a low loss RF filter
The second IF filter can thus have a much narrower bandwidth by virtue of the center frequency being much lower
A higher first IF center frequency moves the image signal further away from the desired signal
3-41
For high-side tuning we have f image = f c + 2 f IF = f c +

21.4 MHz
Double-conversion receivers are more complex to implement
Mixers
The multiplier that is used to implement frequency translation
is often referred to as a mixer
In the world of RF circuit design the term mixer is more appropriate, as an ideal multiplier is rarely available
Instead active and passive circuits that approximate signal multiplication are utilized
The notion of mixing comes about from passing the sum of two
signals through a nonlinearity, e.g.,
y(t) = [a1 x1(t) + a2 x2(t)]2 + other terms
= a12 x12(t) + 2a1a2 x1(t)x2(t) + a22 x22(t)
In this mixing application we are most interested in the center
term
ydesired(t) = 2a1a2 x1(t) x2(t)
Clearly this mixer produces unwanted terms (first and third),

and in general may other terms, since the nonlinearity will have
more than just a square-law input/output characteristic
3-42
A diode or active device can be used to form mixing products

as described above, consider the dual-gate MEtal Semiconductor FET (MESFET) mixer shown below
Nonlinear Device
VRF
zL
VIN
VOUT
VLO
Mixer concept
+5V
R2
10
C3
47pF
C4
5 turns, 28 AWG
.050 I.D.
C1
0.5pF
LO
RF
L2
5 turns, 28 AWG
.050 I.D.
L4
270nH
270nH
G1
G2
C2
0.5pF
0.01uF
L3
L1
C7
D Q1
NE25139 42pF
S
R1
270
C5
47pF
IF
C8
82pF
C8
0.01uF
Dual-Gate MESFET Active Mixer
The double-balanced mixer (DBM), which can be constructed

using a diode ring, provides better isolation between the RF,
LO, and IF ports
When properly balanced the DBM also allows even harmonics
to be suppressed in the mixing operation
3-43
A basic transformer coupled DBM, employing a diode ring, is

shown below, followed by an active version
The DBM is suitable for use as a phase detector in phaselocked loop applications
mixer
LO source
LO
input
D2
D1
vp(t)
RG
RF source
RF
input
vi (t)
D3
RG
D4
IF
out
vo(t)
IF load
RL
Passive Double-Balanced Mixer (DBM)

C9
L1
R3
5V
C8
C11
R4
L2
T1
IF OUT
4:1 (200:50)
TRANSFORMER
C1
RFIN
C2
GND
16
17
GND
IF18
GND
RFBIAS
R1
IF+
MAX9982
RF
TAP
C3
19
20
GND
C10
GND
15
14
13
12
11
LO2
GND
LO2
C7
GND
GND
LO1
LO1
C4
10
VCC
GND
LOSEL
7
GND
5V
VCC
C6
5V
C5
LO SELECT
825 MHz to 915 MHz SiGe High-Linearity Active DBM
3-44
Example 3.9: Single Diode Mixer
3-45
3.2
Angle Modulation
A general angle modulated signal is of the form

xc (t) = Ac cos[c t + (t)]
Definition: Instantaneous phase of xc (t) is
i (t) = c t + (t)
where (t) is the phase deviation
Define: Intsantaneous frequency of xc (t) is
i (t) =
di (t)
d(t)
= c +
dt
dt
where d(t)/dt is the frequency deviation

There are two basic types of angle modulation
1. Phase modulation (PM)
(t) =
kp
m(t)
phase dev. const.
which implies
xc (t) = Ac cos[c t + k p m(t)]

Note: the units of k p is radians per unit of m(t)
If m(t) is a voltage, k p has units of radians/volt
3-46
3.2. ANGLE MODULATION
2. Frequency modulation (FM)

d(t)
=
dt
or
(t) = k f
kf
m(t)
freq. dev. const.
t0
m() d + 0
Note: the units of k f is radians/sec per unit of m(t)

If m(t) is a voltage, k f has units of radians/sec/volt
An alternative expression for k f is
k f = 2 f d
where f d is the frequency-deviation constant in Hz/unit
of m(t)
Example 3.10: Phase and Frequency Step Modulation

Consider m(t) = u(t) v
We form the PM signal
xPM(t) = Ac cos c t + k p u(t) , k p = /3 rad/v

We form the FM signal
xFM(t) = Ac cos c t + 2 f d
m() d , f d = 3 Hz/v
3-47
3 Hz frequency step at t = 0
/3 phase step at t = 0
fc
fc
!1
fc
fc + 3 Hz
!1
!1
!1
Phase Modulation
Frequency Modulation
Phase and frequency step modulation
3.2.1
Narrowband Angle Modulation
Begin by writing an angle modulated signal in complex form
xc (t) = Re Ac e jc t e j(t)
Expand e j(t) in a power series
(t)
xc (t) = Re Ac e jc t 1 + j(t)

2!
The narrowband approximation is |(t)| 1, then
xc (t) Re Ac e jc t + j Ac (t)e jc t
= Ac cos(c t) Ac (t) sin(c t)
3-48
Under the narrowband approximation we see that the signal is

similar to AM except it is carrier plus modulated quadrature
carrier
(t)
+
Ac sin(ct)
NBFM
xc(t)
90o
NBFM modulator block diagram
Example 3.11: Single tone narrowband FM

Consider NBFM with m(t) = cos m t
t
(t) = 2 f d
cos m t d
=
2 f d
fd
sin m t =
sin m t
2 f m
fm
Now,
fd
xc (t) = cos c t
sin m t
fm
fd
Ac cos c t
sin m t sin c t
fm
fd
fd
= Ac cos c t +
sin( f c + f m )t
sin( f c f m )t
2 fm
2 fm
This looks very much like AM

3-49
fc - fm
0
fc + fm
fc
Single tone NBFM spectra
3.2.2
Spectrum of an Angle-Modulated Signal
The development in this obtains the exact spectrum of an angle

modulated carrier for the case of
(t) = sin m t
where is the modulation index for sinusoidal angle modulation
The transmitted signal is of the form
xc (t) = Ac cos c t + sin m t

jc t
j sin m t
= Ac Re e
exp
Note that e j sin m t is periodic with period T = 2/m , thus

we can obtain a Fourier series expansion of this signal, i.e.,
e j sin m t =
3-50
Yn e jnm t
n=
The coefficients are
m /m j sin m t jnm t
Yn =
e
e
dt
2 /m
m /m j (nm t sin m t)
=
e
2 /m
Change variables in the integral by letting x = m t, then d x =

m dt, t = /m x = , and t = /m x =
With the above substitutions, we have

1
Yn =
e j (nx sin x) d x
2
1
=
cos(nx sin x) d x = Jn ()
0
which is a Bessel function of the first kind order n with argument
Jn () Properties
Recurrence equation:
Jn+1() =
n even:
n odd:
2n
Jn () Jn1()
Jn () = Jn ()
Jn () = Jn ()
3-51
1
0.8
0.6
J0()
J1()
0.4
J2()
J3()
0.2
2
!0.2
10
!0.4
Bessel function of order 03 plotted
The zeros of the Bessel functions are important in spectral

analysis
First five Bessel function zeros for order 0 5
J0() = 0
2.40483, 5.52008, 8.65373, 11.7915, 14.9309
J1() = 0
3.83171, 7.01559, 10.1735, 13.3237, 16.4706
J2() = 0
5.13562, 8.41724, 11.6198, 14.796, 17.9598
J3() = 0
6.38016, 9.76102, 13.0152, 16.2235, 19.4094
J4() = 0
7.58834, 11.0647, 14.3725, 17.616, 20.8269
J5() = 0
8.77148, 12.3386, 15.7002, 18.9801, 22.2178
3-52
Spectrum cont.
We obtain the spectrum of xc (t) by inserting the series representation
jc t
xc (t) = Ac Re e
Jn ()e jnm t
n=
= Ac
n=
Jn () cos(c + nm )t
|AcJ1()|
|AcJ-1()|
|AcJ-2()|
|AcJ0()|
For PM
|AcJ2()|
|AcJ3()|
fc + 5fm
fc + 4fm
fc + 3fm
fc + 2fm
fc
fc + fm
fc - fm
|AcJ4()|
|AcJ5()|
fc - 2fm
fc - 3fm
fc - 4fm
|AcJ-3()|
|A J ()|
|AcJ-5()| c -4
fc - 5fm
Amplitude Spectrum
(one-sided)
We see that the amplitude spectrum is symmetrical about f c

due to the symmetry properties of the Bessel functions
sin m t = k p (A sin m t)

m(t)
= kp A
For FM
sin m t = k f
= ( f d / f m )A
A cos m d =
fd
A sin m t
fm
3-53
When is small we have the narrowband case and as gets

larger the spectrum spreads over wider bandwidth
= 0.2, Ac = 1
(narrowband case)
Amplitude
Spectrum
1
0.8
0.6
0.4
0.2
-5
Amplitude
Spectrum
Amplitude
Spectrum
(f - fc)/fm
10
(f - fc)/fm
10
(f - fc)/fm
10
(f - fc)/fm
0.6
0.4
0.2
0
= 2.4048, Ac = 1
(carrier null)
0.8
0.6
0.4
0.2
-5
Amplitude
Spectrum
10
= 1, Ac = 1
0.8
-5
= 3.8317, Ac = 1
(1st sideband null)
0.8
0.6
0.4
0.2
-5
Amplitude
Spectrum
= 8, Ac = 1
(spectrum becoming
wide)
0.8
0.6
0.4
0.2
-5
10
(f - fc)/fm
The amplitude spectrum relative to f c as increases
3-54
Example 3.12: VCO FM Modulator

Consider again single-tone FM, that is m(t) = A cos(2 f m t)
We assume that we know f m and the modulator deviation constant f d
Find A such that the spectrum of xc (t) contains no carrier component
An FM modulator can be implemented using a voltage controlled oscillator (VCO)
sensitivity fd MHz/v
m(t)
VCO
Center
Freq = fc
A VCO used as an FM modulator
The carrier term is Ac J0() cos c t

We know that J0() = 0 for = 2.4048, 5.5201, . . .
The smallest that will make the carrier component zero is
= 2.4048 =
fd
A
fm
which implies that we need to set

A = 2.4048
fm
fd
3-55
Suppose that f m = 1 kHz and f d = 2.5 MHz/v, then we would

need to set
1 103
A = 2.4048
= 9.6192 104
6
2.5 10
3.2.3
Power in an Angle-Modulated Signal
The average power in an angle modulated signal is
xc2(t) = A2c cos2 c t + (t)

1
1
= A2c + A2c cos 2 c t + (t)
2
2
For large f c the second term is approximately zero (why?),

thus
1
Pangle mod = xc2(t) = A2c
2
which makes the power independent of the modulation m(t)
(the assumptions must remain valid however)
3.2.4
Bandwidth of Angle-Modulated Signals
With sinusoidal angle modulation we know that the occupied

bandwidth gets larger as increases
There are an infinite number of sidebands, but
n
lim Jn () lim n = 0,
n
n 2 n!
so consider the fractional power bandwidth

3-56
Define the power ratio

Pcarrier + Pk sidebands
Pr =
=
Ptotal
= J02() + 2
1 2 k
A
n=k
2 c
1 2
A
2 c
Jn2()
Jn2()
n=1
Given an acceptable Pr implies a fractional bandwidth of

B = 2k f m (Hz)
In the text values of Pr 0.7 and Pr 0.98 are single and
double underlined respectively
It turns out that for Pr 0.98 the value of k is IP[1 + ], thus
B = B98 2( + 1) f m sinusoidal mod only
For arbitrary modulation m(t), define the deviation ratio
peak freq. deviation

fd
D=
=
max |m(t)|
bandwidth of m(t)
W
In the sinusoidal modulation bandwidth definition let D
and f m W , then we obtain what is known as Carsons rule
B = 2(D + 1)W
Another view of Carsons rule is to consider the maximum frequency deviation f = max |m(t)| f d , then B =
2(W + f )
3-57
Two extremes in angle modulation are

1. Narrowband: D 1 B = 2W
2. Wideband: D 1 B = 2DW = 2 f
Example 3.13: Single Tone FM

Consider an FM modulator for broadcasting with
6
xc (t) = 100 cos 2(101.1 10 )t + (t)
where f d = 75 kHz/v and
m(t) = cos 2(1000)t v
The value for the transmitter is
fd
75 103
=
A=
= 75
fm
103
Note that the carrier frquency is 101.1 MHz and the peak deviation is f = 75 kHz
The bandwidth of the signal is thus
B 2(1 + 75)1000 = 152 kHz

B = 2( + 1)fm
Amplitude
Spectrum
17.5
15
12.5
10
7.5
5
2.5
-76
-50
101.1 MHz - 76 kHz

3-58
101.1 MHz
50
76
(f - 101.1 MHz)
1 kHz
100
101.1 MHz + 76 kHz

Suppose that this signal is passed through an ideal bandpass

filter of bandwidth 11 kHz centered on f c = 101.1 MHz, i.e.,
f fc
f + fc
H( f ) =
+
11000
11000
The carrier term and five sidebands either side of the carrier
pass through this filter, resulting an output power of
5
2
A
Pout = c J02(75) + 2
Jn2(75) = 241.93 W
2
n=1
Note the input power is A2c /2 = 5000 W
Example 3.14: Two Tone FM

Finding the exact spectrum of an angle modulated carrier is not
always possible
The single-tone sinusoid case can be extended to multiple tone
with increasing complexity
Suppose that
m(t) = A cos 1t + B cos 2t
The phase deviation is given by 2 f d times the integral of the
frequency modulation, i.e.,
(t) = 1 sin 1t + 2 sin 2t
where 1 = A f d / f 1 and 2 = A f d / f 2
3-59
The transmitted signal is of the form
xc (t) = Ac cos c t + 1 sin 1t + 2 sin 2t
= Ac Re e jc t e j1 sin 1t e j2 sin 2t
We have previously seen that via Fourier series expansion

e j1 sin 1t =
e j2 sin 1t =
n=
Jn (1)e jn1t
Jn (2)e jn2t
n=
Inserting the above Fourier series expansions into xc (t), we

have
jc t
jn1 t
xc (t) = Ac Re e
Jn (1)e
Jm (2)e jm2t
= Ac
n=
n= m=
m=
Jn (1)Jm (2) cos(c + n1 + m2)t
The nonlinear nature of angle modulation is clear, since we see

not only components at c + n1 and c + m2, but also at all
combinations of c + n1 + m2
To find the bandwidth of this signal we can use Carsons rule
(the sinusoidal formula only works for one tone)
Recall that B = 2( f + W ), where f is the peak frequency
deviation
3-60
The frequency deviation is
1 d
f i (t) =
1 sin 1t + 2 sin 2t
2 dt
= 1 f 1 cos(2 f 1t) + 2 f 2 cos(2 f 2t) Hz
The maximum of f i (t), in this case, is 1 f 1 + 2 f 2
Suppose 1 = 2 = 2 and f 2 = 10 f 1, then we see that W =
f 2 = 10 f 1 and
B = 2(W + f ) = 2 10 f 1 +2( f 1 +10 f 1) = 2(32 f 1) = 64 f 1
Amplitude
Spectrum
0.35
0.3
0.25
0.2
0.15
0.1
0.05
1 = 2 = 2, f2 = 10f 1
B = 2(W + f) = 2(10f1 + 2(11)f1) = 64f1
-40
-20
20
40
(f - fc)
f1
Example 3.15: Bandlimited Noise PM and FM

This example will utilize simulation to obtain the spectrum of
an angle modulated carrier
The message signal in this case will be bandlimited noise having lowpass bandwidth of W Hz
3-61
In MATLAB we can generate Gaussian amplitude distributed

white noise using randn() and then filter this noise using a
high-order lowpass filter (implemented as a digital filter in this
case)
We can then use this signal to phase or frequency modulate
a carrier in terms of the peak phase deviation, derived from
knowledge of max[|(t)|]
3-62
3.2.5
Narrowband-to-Wideband Conversion
Narrowband FM
Carrier = fc1
Peak deviation = fd1
Deviation ratio = D1
xn
Freq.
Multiplier
Narrowband
FM Modulator
(similar to AM)
m(t)
Wideband FM
Carrier = nfc1
Peak deviation = nfd1
Deviation ratio = nD1
Ac1cos[ct + (t)]
Ac2cos[nct + n(t)]
BPF
LO
xc(t)
Frequency
translate
narrowband-to-wideband conversion
Narrowband FM can be generated using an AM-type modulator as discussed earlier (a VCO is not required, so the carrier
source can be very stable)
A frequency multiplier, using say a nonlinearity, can be used
to make the signal wideband FM, i.e.,
n
Ac1 cos[c t + (t)] Ac2 cos[nc t + n(t)]
so the modulator deviation constant of f d1 becomes n f d1
3.2.6
Demodulation of Angle-Modulated Signals
To demodulate FM we require a discriminator circuit, which

gives an output which is proportional to the input frequency
deviation
For an ideal discriminator with input
xr (t) = Ac cos[c t + (t)]
3-63
the output is
y D (t) =
1
d(t)
KD
2
dt
Ideal
Discriminator
xc(t)
yD(t)
Ideal FM discriminator
For FM
so
(t) = 2 f d
m() d
y D (t) = K D f d m(t)
Output
Signal (voltage)
slope = KD
fc
Input
Frequency
Ideal discriminator I/O characteristic
For PM signals we follow the discriminator with an integrator

xr(t)
Ideal
Discrim.
yD(t)
Ideal discriminator with integrator for PM demod

3-64
For PM (t) = k p m(t) so

y D (t) = K D k p m(t)
We now consider approximating an ideal discriminator with:
e(t)
xr(t)
Envelope
Detector
yD(t)
Ideal discriminator approximation
If xr (t) = Ac cos[c t + (t)]
d xr (t)
d
e(t) =
= Ac c +
sin c t + (t)
dt
dt
This looks like AM provided
d(t)
< c
dt
which is only reasonable
Thus
y D (t) = Ac
d(t)
= 2 Ac f d m(t) (for FM)
dt
Relative to an ideal discriminator, the gain constant is

K D = 2 Ac
To eliminate any amplitude variations on Ac pass xc (t) through
a bandpass limiter
3-65
xr(t)
Limiter
e(t)
BPF
Envelope
Detector
yD(t)
Bandpass Limiter
FM discriminator with bandpass limiter
We can approximate the differentiator with a delay and subtract

operation
e(t) = xr (t) xr (t )
since
e(t)
xr (t) xr (t ) d xr (t)
= lim
=
,
0
0
dt
lim
thus
e(t)
d xr (t)
dt
In a discrete-time implementation (DSP), we can perform a

similar operation, e.g.
e[n] = x[n] x[n 1]
Example 3.16: Complex Baseband Discriminator

A DSP implementation in MATLAB that works with complex
baseband signals (complex envelope) is the following:
function disdata = discrim(x)
% function disdata = discrimf(x)
% x is the received signal in complex baseband form
%
% Mark Wickert
3-66
xI=real(x); % xI is the real part of the received signal

xQ=imag(x); % xQ is the imaginary part of the received signal
N=length(x); % N is the length of xI and xQ
b=[1 -1];
% filter coefficients
a=[1 0];
% for discrete derivative
der_xI=filter(b,a,xI); % derivative of xI,
der_xQ=filter(b,a,xQ); % derivative of xQ
% normalize by the squared envelope acts as a limiter
disdata=(xI.*der_xQ-xQ.*der_xI)./(xI.2+xQ.2);
To understand the operation of discrim() start with a general angle modulated and obtain the complex envelope
xc (t) = Ac cos(c t + (t))
j(t) jc t
= Re Ac e
e
jc t
= Ac Re [cos (t) + j sin (t)]e
The complex envelope is
xc (t) = cos (t) + j sin (t) = x I (t) + j x Q (t)
where x I and x Q are the in-phase and quadrature signals respectively

A frequency discriminator obtains d(t)/dt
In terms of the I and Q signals,
(t) = tan1
x Q (t)
x I (t)
The derivative of (t) is
d(t)
1
d x Q (t)
=
dt
1 + (x Q (t)/x I (t))2 dt x I (t)
x I (t)x Q (t) x I (t)x Q (t)
=
x I2(t) + x Q2 (t)
3-67
In the DSP implementation x I [n] = x I (nT ) and x Q [n] =

x Q (nT ), where T is the sample period
The derivatives, x I (t) and x Q (t) are approximated by the backwards difference x I [n] x I [n 1] and x Q [n] x Q [n 1]
respectively
To put this code into action, consider a single tone message at
1 kHz with = 2.4048
(t) = 2.4048 cos(2(1000)t)
The complex baseband (envelope) signal is
xc (t) = e j(t) = e j2.4048 cos(2(1000)t)
A MATLAB simulation that utilizes the function Discrim()
is:
>>
>>
>>
>>
>>
>>
>>
>>
>>
>>
>>
>>
>>
>>
>>
>>
3-68
n = 0:5000-1;
m = cos(2*pi*n*1000/50000); % sampling rate = 50 kHz
xc = exp(j*2.4048*m);
y = Discrim(xc);
% baseband spectrum plotting tool using psd()
bb_spec_plot(xc,211,50);
axis([-10 10 -30 30])
grid
xlabel(Frequency (kHz))
ylabel(Spectral Density (dB))
t = n/50;
plot(t(1:200),y(1:200))
axis([0 4 -.4 .4])
grid
xlabel(Time (ms))
ylabel(Amplitude of y(t))
30
Note: no carrier
term since =
2.4048
Spectral Density (dB)
20
10
0
10
20
30
10
2
0
2
Frequency (kHz)
10
0.4
0.3
Amplitude of y(t)
0.2
0.1
0
0.1
0.2
0.3
0.4
0.5
1.5
2
Time (ms)
2.5
3.5
Baseband FM spectrum and demodulator output wavefrom
3-69
Analog Circuit Implementations

A simple analog circuit implementation is an RC highpass filter followed by an envelope detector
|H(f)|
1
0.707
Linear operating
region converts
FM to AM
Highpass
fc
Highpass
1
2RC
Re Ce
Envelope Detector
RC highpass filter + envelope detector discriminator (slope detector)
For the RC highpass filter to be practical the cutoff frequency

must be reasonable
Broadcast FM radio typically uses a 10.7 MHz IF frequency,
which means the highpass filter must have cutoff above this
frequency
A more practical discriminator is the balanced discriminator,
which offers a wider linear operating range
3-70
Filter Amplitude
Response
|H2(f)|
|H1(f)|
f1
Filter Amplitude
Response
f2
f
Linear region
|H1(f)| - |H2(f)|
R
xc(t)
f1
L1
C1
Re
Ce
L2
C2
Re
Ce
yD(t)
f2
Bandpass Envelope Detectors
Balanced discriminator operation (top) and a passive implementation

(bottom)
3-71
FM Quadrature Detectors
xc(t)
C1
xquad(t)
Lp
Usually a
xout(t) lowpass
filter is
added here
Tank circuit
Cp tuned to fc
Quadrature detector schematic
In analog integrated circuits used for FM radio receivers and

the like, an FM demodulator known as a quadrature detector
or quadrature discriminator, is quite popular
The input FM signal connects to one port of a multiplier (product device)
A quadrature signal is formed by passing the input to a capacitor series connected to the other multiplier input and a parallel
tank circuit resonant at the input carrier frequency
The quadrature circuit receives a phase shift from the capacitor
and additional phase shift from the tank circuit
The phase shift produced by the tank circuit is time varying in
proportion to the input frequency deviation
A mathematical model for the circuit begins with the FM input
signal
xc (t) = Ac [c t + (t)]
3-72
3.3. INTERFERENCE
The quadrature signal is
(t)
xquad(t) = K 1 Ac sin c t + (t) + K 2
dt
where the constants K 1 and K 2 are determined by circuit parameters
The multiplier output, assuming a lowpass filter removes the
sum terms, is
1
d(t)
xout(t) = K 1 A2c sin K 2
2
dt
By proper choice of K 2 the argument of the sin function is
small, and a small angle approximation yields
1
d(t) 1
xout(t) K 1 K 2 A2c
= K 1 K 2 A2c K D m(t)
2
dt
2
3.3
Interference
Interference is a fact of life in communication systems. A through

understanding of interference requires a background in random signals analysis (Chapter 6 of the text), but some basic concepts can be
obtained by considering a single interference at f c + f i that lies close
to the carrier f c
3-73
Interference in Linear Modulation

Single-Sided Spectrum
3.3.1
Xr(f)
Ac
1
A
2 m
fc - fm
fc
1
A
2 m
fc + fm
Ai
fc + fi
AM carrier with single tone interference
If a single tone carrier falls within the IF passband of the receiver what problems does it cause?
Coherent Demodulator
xr (t) = Ac cos c t + Am cos m t cos c t

+ Ai cos(c + i )t
We multiply xr (t) by 2 cos c t and lowpass filter
y D (t) = Am cos m t + Ai cos i t

interference
Envelope Detection: Here we need to find the received envelope relative to the strongest signal present
Case Ac Ai
We will expand xr (t) in complex envelope form by first

noting that
Ai cos(c + i )t = Ai cos i t cos c t Ai sin i t sin c t
3-74
3.3. INTERFERENCE
now,
so
xr (t) = Re Ac + Am cos m t + Ai cos i t
j Ai sin i t e jc t
jc t
= Re R(t)e
R(t) = | R(t)|
= (Ac + Am cos m t + Ai cos i t)2

1/2
2
+ (Ai sin i t)
Ac + Am cos m t + Ai cos i t
assuming that Ac Ai
Finally,
y D (t) Am cos m t + Ai cos i t

interference
Case Ai >> Ac
Now the interfering term looks like the carrier and the remaining terms look like sidebands, LSSB sidebands relative to f c + f i to be specific
From SSB envelope detector analysis we expect
1
Am cos(i + m )t + Ac cos i t
2
1
+ Am cos(i m )t
2
and we conclude that the message signal is lost!
y D (t)
3-75
3.3.2
Interference in Angle Modulation
Initially assume that the carrier is unmodulated

xr (t) = Ac cos c t + Ai cos(c + i )t
In complex envelope form we have
xr (t) = Re (Ac + Ai cos i t j Ai sin i t)e jc t

= Ac + Ai cos i t j Ai sin i t
with R(t)
The real envelope or envelope magnitude is, R(t) = | R(t)|,
R(t) = (Ac + Ai cos i t)2 + (Ai sin i t)2

and the envelope phase is
(t) = tan1
Ai sin i t
Ac + Ai cos i t
For future reference note that:

tan
|x|1
x3 x5 x7
x=x
+
+ x
3
5
7
We can thus write that
xr (t) = R(t) cos c t + (t)

If Ac Ai
Ai
xr (t) (Ac + Ai cos i t) cos c t +
sin i t
Ac

R(t)
(t)
3-76
3.3. INTERFERENCE
Case of PM Demodulator: The discriminator recovers d(t)/dt,

so the output is followed by an integrator
y D (t) = K D
Ai
sin i t
Ac
Case of FM Demodulator: The discriminator output is used directly to obtain d(t)/dt

y D (t) =
1
Ai d
Ai
KD
sin i t = K D f i cos i t
2
Ac dt
Ac
We thus see that the interfering tone appears directly in the

output for both PM and FM
For the case of FM the amplitude of the tone is proportional to
the offset frequency f i
For f i > W , recall W is the bandwidth of the message m(t),
a lowpass filter following the discriminator will remove the
interference
When Ai is similar to Ac and larger, the above analysis no
longer holds
In complex envelope form
jc t
ji t
xr (t) = Re Ac + Ai e
e
The phase of the complex envelope is
(t) =
A c + Ai e
ji t
= tan1
Ai sin i t
Ac + Ai cos i t
3-77
We now consider Ai Ac and look at plots of (t) and the

derivative
(t)
0.1
d(t)/dt
0.05
!1
!0.5
Ai = 0.1Ac
fi = 1
0.5
!1
!0.5
0.5
!0.6
t
1
!1
!0.5
Ai = 0.9Ac
fi = 1
0.5
!30
!0.5
!40
!1
!50
70
d(t)/dt
60
50
1
!0.5
Ai = 1.1Ac
fi = 1
!10
!20
(t)
!0.5
d(t)/dt
0.5
!1
!0.2
0.5
!0.4
!0.1
!1
0.4
0.2
!0.05
(t)
0.6
!1
0.5
40
30
20
10
!2
!3
!1
!0.5
0.5
Phase deviation and discriminator outputs when Ai Ac
We see that clicks (positive or negative spikes) occur in the

discriminator output when the interference levels is near the
signal level
When Ai Ac the message signal is entirely lost and the
discriminator is said to be operating below threshold
3-78
3.3. INTERFERENCE
To better see what happens when we approach threshold, apply

single tone FM to the carrier
(t) = Ac e j Am cos(m t) + Ai e ji t
Plot the discriminator output d(t)/dt with Am = 5, f m = 1,

f i = 3, and various values of Ai
Ai = 0.005, 30
fi = 3
20
Am = = 5,
10
fm = 1
!1
!0.5
!10
Ai = 0.5,
fi = 3
Am = = 5,
fm = 1
0.5
!1
!0.5
!10
!20
!20
!30
!30
20
!1
Ai = 0.1,
30
fi = 3
20
Am = = 5,
10
fm = 1
d(t)/dt
!0.5
!20
!40
!60
!80
0.5
d(t)/dt
d(t)/dt
0.5
d(t)/dt
!1
!0.5
0.5
!100
Ai = 0.9,
fi = 3
Am = = 5,
fm = 1
!200
!300
!400
Discriminator outputs as Ai approaches Ac with single tone FM = 5
The Use of Preemphasis in FM

We have seen that when Ai is small compared to Ac the interference level in the case of FM demodulation is proportional
to f i
The generalization from a single tone interferer to background
noise (text Chapter 6), shows a similar behavior, that is wide
3-79
bandwidth noise entering the receiver along with the desired

FM signal creates noise in the discriminator output that has
amplitude proportional with frequency (noise power proportional to the square of the frequency)
In FM radio broadcasting a preemphasis boosts the high frequency content of the message signal to overcome the increased
noise background level at higher frequencies, with a deemphasis filter used at the discriminator output to gain equalize/flatten the end-to-end transfer function for the modulation
m(t)
Discriminator Output
with Interference/Noise
No preemphasis
With preemphasis
Message Bandwidth
0
f1
FM
Mod
r
HP(f)
f2
r
Discrim
C
Hd(f)
|Hd(f)|
|Hp(f)|
f1
f1
FM broadcast preemphasis and deemphasis filtering
The time constant for these filters is RC = 75 s ( f 1 =

1/(2 RC) = 2.1 kHz ), with a high end cutoff of about f 2 =
30 kHz
3-80
3.4. FEEDBACK DEMODULATORS
3.4
Feedback Demodulators
The discriminator as described earlier first converts and FM

signal to and AM signal and then demodulates the AM
The phase-locked loop (PLL) offer a direct way to demodulate
FM and is considered a basic building block by communication
system engineers
3.4.1
Phase-Locked Loops for FM Demodulation
The PLL has many uses and many different configurations,

both analog and DSP based
We will start with a basic configuration for demodulation of
FM
Kd
Phase
Detector
xr(t)
ed(t)
eo(t)
Loop
Filter
Loop
Amplifier
ev(t)
VCO
xr(t)
-eo(t)
Sinusoidal
phase detector
with inverting
input
Basic PLL block diagram

3-81
Let
xr (t) = Ac cos c t + (t)
eo (t) = Av sin c t + (t)
Note: Frequency error may be included in (t) (t)

Assume a sinusoidal phase detector with an inverting operation
is included, then we can further write
ed (t) =
1
Ac Av K d sin (t) (t)
2
In the above we have assumed that the double frequency

term is removed (e.g., by the loop filter eventually)
Note that for the voltage controlled oscillator (VCO) we have
the following relationship
ev(t)
VCO
Kv
o + d
dt
but
d (t)
= K v ev (t) rad/s
dt
t
(t) = K v
ev () d
In its present form the PLL is a nonlinear feedback control
system
3-82
(t)
(t)
ed(t)
sin( )
Loop
nonlinearity
f(t)
Loop filter
impulse response
(t)
ev(t)
Nonlinear feedback control model
To shown tracking we first consider the loop filter to have impulse response (t) (a straight through connection or unity gain
amplifier)
The loop gain is now defined as
1
K t = Ac Av K d K v rad/s
2
The VCO output is

(t) = K t
or
sin[() ()] d
d(t)
= K t sin[(t) (t)]
dt
Let (t) = (t) (t) and apply an input frequency step ,

i.e.,
d(t)
= u(t)
dt
Now,
d(t)
d(t)
=
= K t sin (t), t 0
dt
dt
3-83
We can now plot d/dt versus , which is known as a phase

plane plot
+ Kt
d(t)/dt
- Kt
Stable
lock point
> 0
(t)
ss
Phase plane plot (1st-order PLL)
(t)
+ K t sin (t) = u(t)
dt
At t = 0 the operating point is at B
d
> 0 d is positive
dt
d
Since dt is positive if
< 0 d is negative
dt
Since dt is positive if
therefore the steady-state operating point is at A

The frequency error is always zero in steady-state
The steady-state phase error is ss
Note that for locking to take place, the phase plane curve
must cross the d/dt = 0 axis
3-84
The maximum steady-state value of the loop can handle is

thus K t
The total lock range is then
c K t c + K t 2K t
For a first-order loop the lock range and the hold-range

are identical
For a given the value of ss can be made small by increasing the loop gain, i.e.,
ss = sin1
Kt
Thus for large K t the in-lock operation of the loop can be modeled with a fully linear model since (t) (t) is small, i.e.,
sin[(t) (t)] (t) (t)
The s-domain linear PLL model is the following

(s)
(s)
+
F(s)
AcAvKd/2
Ev(s)
(s)
Kv/s
Linear PLL model
Solving for (s) we have
or
Kt
(s) =
(s) (s) F(s)
s
Kt
Kt
(s) 1 +
F(s) = (s)F(s))
s
s
3-85
Finally, the closed-loop transfer function is

K
t
F(s)
(s)
K t F(s)
s
H (s) =
=
=
(s) 1 + Ks t F(s) s + K t F(s)
First-Order PLL
Let F(s) = 1, then we have
H (s) =
Kt
Kt + s
Consider the loop response to a frequency step, that is for FM,

we assume m(t) = Au(t), then
t
(t) = Ak f
u() d
so
(s) =
Ak f
s2
The VCO phase output is

(s) =
Ak f K t
s 2(K t + s)
The VCO control voltage should be closely related to the applied FM message
To see this write
E v (s) =
3-86
Ak f
s
Kt
(s) =
Kv
K v s(s + K t )
Partial fraction expanding yields,
Ak f 1
1
E v (s) =
Kv s s + Kt
thus
Ak f
K t t
ev (t) =
1e
u(t)
Kv
m(t)
1st-Order PLL frequency step response at VCO input K v ev (t)/k f
In general,
(s) =
so
E v (s) =
k f M(s)
s
k f M(s) s
kf
Kt
Kt
M(s)
s
Kv s + Kt
Kv s + Kt
Now if the bandwidth of m(t) is W K t , then

E v (s)
kf
kf
M(s) ev (t)
m(t)
Kv
Kv
The first-order PLL has limited lock range and always has a
nonzero steady-state phase error when the input frequency is
offset from the quiescent VCO frequency
3-87
Increasing the loop gain appears to help, but the loop bandwidth becomes large as well, which allows more noise to enter
the loop
Spurious time constants which are always present, but not a
problem with low loop gains, are also a problem with high
gain first-order PLLs
Example 3.17: First-Order PLL Simulation Example

Tool such as MATLAB, MATLAB with Simulink, VisSim/Comm,
and others provide an ideal environment for simulating PLLs
at the system level
Circuit level simulation of PLLs is very challenging due to the
need to simulate every cycle of the VCO
The most realistic simulation method is to use the actual bandpass signals, but since the carrier frequency must be kept low
to minimize the simulation time, we have difficulties removing
the double frequency term from the phase detector output
By simulating at baseband, using the nonlinear loop model,
many PLL aspects can be modeled without worrying about
how to remove the double frequency term
A complex baseband simulation allows further capability,
but will not be discussed at his time
The most challenging aspect of the simulation is dealing with
the integrator found in the VCO block (K v /s)
3-88
We consider a discrete-time simulation where all continuoustime waveforms are replaced by their discrete-time counterparts, i.e., x[n] = x(nT ) = x(n/ f s), where f s is the sample
frequency and T = 1/ f s is the sampling period
The input/output relationship of an integration block can be
approximated via the trapezoidal rule
T
y[n] = y[n 1] +
x[n] + x[n 1]
2
function [theta,ev,phi_error] = PLL1(phi,fs,loop_type,Kv,fn,zeta)

% [theta, ev, error, t] = PLL1(phi,fs,loop_type,Kv,fn,zeta)
%
%
T = 1/fs;
Kv = 2*pi*Kv; % convert Kv in Hz/v to rad/s/v
if loop_type == 1
% First-order loop parameters
Kt = 2*pi*fn; % loop natural frequency in rad/s
elseif loop_type == 2
% Second-order loop parameters
Kt = 4*pi*zeta*fn; % loop natural frequency in rad/s
a = pi*fn/zeta;
else
error(Loop type must be 1 or 2);
end
% Initialize integration approximation filters
filt_in_last = 0; filt_out_last = 0;
vco_in_last = 0; vco_out = 0; vco_out_last = 0;
% Initialize working and final output vectors
n = 0:length(phi)-1;
theta = zeros(size(phi));
ev = zeros(size(phi));
phi_error = zeros(size(phi));
% Begin the simulation loop
3-89
for k = 1:length(n)
phi_error(k) = phi(k) - vco_out;
% sinusoidal phase detector
pd_out = sin(phi_error(k));
% Loop gain
gain_out = Kt/Kv*pd_out; % apply VCO gain at VCO
% Loop filter
if loop_type == 2
filt_in = a*gain_out;
filt_out = filt_out_last + T/2*(filt_in + filt_in_last);
filt_in_last = filt_in;
filt_out_last = filt_out;
filt_out = filt_out + gain_out;
else
filt_out = gain_out;
end
% VCO
vco_in = filt_out;
vco_out = vco_out_last + T/2*(vco_in + vco_in_last);
vco_in_last = vco_in;
vco_out_last = vco_out;
vco_out = Kv*vco_out; % apply Kv
% Measured loop signals
ev(k) = vco_in;
theta(k) = vco_out;
end
To simulate a frequency step we input a phase ramp

Consider an 8 Hz frequency step turning on at 0.5 s and a -12
Hz frequency step turning on at 1.5 s
(t) = 2 8(t 0.5)u(t 0.5) 12(t 1.5)u(t 1.5)

>>
>>
>>
>>
>>
>>
>>
>>
3-90
t = 0:1/1000:2.5;
idx1 = find(t>= 0.5);
idx2 = find(t>= 1.5);
phi1(idx1) =2*pi* 8*(t(idx1)-0.5).*ones(size(idx1));
phi2(idx2) = 2*pi*12*(t(idx2)-1.5).*ones(size(idx2));
phi = phi1 - phi2;
[theta, ev, phi_error] = PLL1(phi,1000,1,1,10,0.707);
plot(t,phi_error); % phase error in radians
Phase Error, (t) (t), (rad)
0.927
With Kt = 2(10) and

Kv = 2(1) rad/s/v, we
know that with the 8
Hz step ev(t) = 8, so
working backwards,
sin( - ) = 8/10 = 0.8
and - = 0.927 rad.
0.5
0.5
-0.412
0
0.5
Time (s)
1.5
2.5
Phase error for input within lock range
In the above plot we see the finite rise-time due to the loop gain
being 2(10)
This is a first-order lowpass step response
The loop stays in lock since the frequency swing either side of
zero is within the 10 Hz lock range
Suppose now that a single positive frequency step of 12 Hz is
applied, the loop unlocks and cycle slips indefinitely; why?
>>
>>
>>
>>
>>
>>
phi = 12/8*phi1; % scale frequency step from 8 Hz to 12 Hz

subplot(211)
plot(t,phi_error)
subplot(212)
plot(t,sin(phi_error))
3-91
Phase Error sin((t) (t))
Phase Error ((t) (t))
100
le
Cyc
50
0.5
0.5
Time (s)
slips
1.5
2.5
1.5
2.5
1
0.5
0
0.5
1
Time (s)
Phase error for input exceeding lock range by 2 Hz
By plotting the true phase detector output, sin[(t) (t)], we

see that the error voltage is simply not large enough to pull the
VCO frequency to match the input which is offset by 12 Hz
In the phase plane plot shown earlier, this scenario corresponds
to the trajectory never crossing zero
3-92
Second-Order Type II PLL

To mitigate some of the problems of the first-order PLL, we
can include a second integrator in the open-loop transfer function
A common loop filter for building a second-order PLL is an
integrator with lead compensation
s+a
F(s) =
s
The resulting PLL is sometimes called a perfect second-order
PLL since two integrators are now in the transfer function
In text Problem 3.52 you analyze the lead-lag loop filter
s+a
F(s) =
s+
which creates an imperfect, or finite gain integrator, secondorder PLL
Returning to the integrator with phase lead loop filter, the closedloop transfer function is
H (s) =
K t F(s)
K t (s + a)
= 2
s + K t F(s) s + K t s + K t a
The transfer function from the input phase to the phase error
(t) is
(s) (s) (s)
=
(s)
(s)
s2
1 H (s) = 2
s + Kt s + Kt a
3-93
In standard second-order system notation we can write the denominator of 1 H (s) as

s 2 + K t s + K t a = s 2 + 2 n s + n2
where
K t a = natural frequency in rad/s
1 Kt
=
= damping factor
2 a
n =
For an input frequency step the steady-state phase error is zero

Note the hold-in range is infinite, in theory, since the integrator contained in the loop filter has infinite DC gain
To verify this we can use the final value theorem
s
ss = lim s
s0
s2 s2 + Kt s + Kt a
s
= lim 2
=0
s0 s + K t s + K t a
In exact terms we can find (t) by inverse Laplace transforming
(s) = 2
s + 2 n s + n2
The result for < 1 is
3-94
n t
2
(t) =
e
sin n 1 t u(t)
2
n 1
Example 3.18: Second-Order PLL Simulation Example

As a simulation example consider a loop designed with f n =
10 Hz and = 0.707
K t = 2 n = 2 0.707 2 10 = 88.84
n
2 10
a=
=
= 44.43
2
2 0.707
The simulation code of Example 3.17 includes the needed loop
filter via a software switch
The integrator that is part of the loop filter is implemented using the same trapezoidal formula as used in the VCO
We input a 40 Hz frequency step and observe the VCO control
voltage (ev (t)) as the loop first slips cycles, gradually pulls in,
tracks the input signal offset by 40 Hz
The VCO gain K v = 1 v/Hz or 2 rad/s, so ev (t) effectively
corresponds to the VCO frequency deviation in Hz
>>
>>
>>
>>
>>
>>
t = 0:1/1000:2.5;
idx1 = find(t>= 0.5);
phi(idx1) = 2*pi*40*(t(idx1)-0.5).*ones(size(idx1));
plot(t,ev)
axis([0.4 0.8 -10 50])
3-95
VCO Control Voltage ev(t) (Kv = 1 Hz/v)
50
Cycle slipping, but

pulling in to match
40 Hz frequency step
40
30
Cycle slipping stops,

and the loop settles
20
10
0
10
0.4
0.45
0.5
0.55
0.6
Time (s)
0.65
0.7
0.75
0.8
VCO control voltage for a 40 Hz frequency step
Example 3.19: Bandpass Simulation of FM Demodulation

Baseband PLL simulations are very useful and easy to implement, but sometimes a full bandpass level simulation is required
The MATLAB simulation file PLL1.m is modified to allow
passband simulation via the function file PLL2.m
The phase detector is a multiplier followed by a lowpass filter
to remove the double frequency term
function [theta, ev, phi_error] = PLL2(xr,fs,loop_type,Kv,fn,zeta)
% [theta, ev, error, t] = PLL2(xr,fs,loop_type,Kv,fn,zeta)
%
3-96
%
T = 1/fs;
% Set the VCO quiescent frequency in Hz
fc = fs/4;
% Design a lowpass filter to remove the double freq term
[b,a] = butter(5,2*1/8);
fstate = zeros(1,5); % LPF state vector
Kv = 2*pi*Kv; % convert Kv in Hz/v to rad/s/v
if loop_type == 1
% First-order loop parameters
Kt = 2*pi*fn; % loop natural frequency in rad/s
elseif loop_type == 2
% Second-order loop parameters
Kt = 4*pi*zeta*fn; % loop natural frequency in rad/s
a = pi*fn/zeta;
else
error(Loop type musy be 1 or 2);
end
% Initialize integration approximation filters
filt_in_last = 0; filt_out_last = 0;
vco_in_last = 0; vco_out = 0; vco_out_last = 0;
% Initialize working and final output vectors
n = 0:length(xr)-1;
theta = zeros(size(xr));
ev = zeros(size(xr));
phi_error = zeros(size(xr));
% Begin the simulation loop
for k = 1:length(n)
% Sinusoidal phase detector (simple multiplier)
phi_error(k) = 2*xr(k)*vco_out;
% LPF to remove double frequency term
[phi_error(k),fstate] = filter(b,a,phi_error(k),fstate);
pd_out = phi_error(k);
% Loop gain
gain_out = Kt/Kv*pd_out; % apply VCO gain at VCO
% Loop filter
if loop_type == 2
filt_in = a*gain_out;
filt_out = filt_out_last + T/2*(filt_in + filt_in_last);
3-97
filt_in_last = filt_in;
filt_out_last = filt_out;
filt_out = filt_out + gain_out;
else
filt_out = gain_out;
end
% VCO
vco_in = filt_out + fc/(Kv/(2*pi)); % bias to quiescent freq.
vco_out = vco_out_last + T/2*(vco_in + vco_in_last);
vco_in_last = vco_in;
vco_out_last = vco_out;
vco_out = Kv*vco_out; % apply Kv;
vco_out = sin(vco_out); % sin() for bandpass signal
% Measured loop signals
ev(k) = filt_out;
theta(k) = vco_out;
end
Note that the carrier frequency is fixed at f s /4 and the lowpass

filter cutoff frequency is fixed at f s /8
The double frequency components out of the phase detector
are removed with a fifth-order Butterworth lowpass filter
The VCO is modified to include a bias that shifts the quiescent
frequency to f c = f s /4
The VCO output is not simply a phase deviation, but rather a
sinusoid with argument the VCO output phase
We will test the PLL using a single tone FM signal
>>
>>
>>
>>
>>
>>
>>
>>
3-98
t = 0:1/4000:5;
xr = cos(2*pi*1000*t+2*sin(2*pi*10*t));
psd(xr,214,4000)
axis([900 1100 -40 30])
% Process signal through PLL
[theta, ev, phi_error] = PLL2(xr,4000,1,1,50,0.707);
plot(t,ev)
axis([0 1 -25 25])
30
Power Spectrum of xr(t) (dB)
20
10
0
10
20
30
40
900
920
940
960
980 1000 1020

Frequency (Hz)
1040
1060
1080
1100
Single tone FM input spectrum having f m = 10 Hz and f = 20 Hz
VCO Control Voltage ev(t) (Kv = 1 Hz/v)
25
20
15
10
5
0
5
10
15
20
25
0.1
0.2
0.3
0.4
0.5
0.6
Time (s)
0.7
0.8
0.9
Recovered modulation at VCO input, ev (t)
3-99
3.4.2
PLL Frequency Synthesizers
A frequency synthesizer is used to generate a stable, yet programmable frequency source

A frequency synthesizer is often used to allow digital tuning of
the local oscillator in a communications receiver
One common frequency synthesis type is known as indirect
synthesis
With indirect synthesis a PLL is used to create a stable frequency source
The basic block diagram of an indirect frequency synthesizer
is the following
fref
1
M
fref
Freq Div M
Phase
Detector
Loop
Filter
fout
N
VCO
fout
1
N
Freq Div
Indirect frequency synthesis using a PLL
When locked the frequency error is zero, thus

f out =
3-100
N
f ref
M
Example 3.20: A PLL Synthesizer for Broadcast FM

In this example the synthesizer will provide the local oscillator
signal for frequency converting the FM broadcast band from
88.1 to 107.9 MHz down to an IF of 10.7 MHz
The minimum channel spacing should be 200 kHz
We will choose high-side tuning for the LO, thus
88.1 + 10.7 f LO 107.9 + 10.7 MHz
98.8 f LO 118.6 MHz
The step size must be 200 kHz so the frequency must be
no larger than 200 kHz
To reduce the maximum frequency into the divide by counter
a frequency offset scheme will be employed
The synthesizer with offset oscillator is the following
fref
Freq Div
1
M
Phase
Detector
Loop
Filter
fref
M
= 200 kHz
fmix
N
1
N
VCO
fout
fmix
Difference
Freq Div Frequency
foffset
FM broadcast band synthesizer producing f LO for f IF = 10.7 MHz

3-101
Choose f offset < f out then f mix = f out f offset, and for locking
f ref
f mix
N f ref
=
f out =
+ f offset
M
N
M
Note that Fmix = N f ref/M and f out = f mix + f offset, by

virtue of the low side tuning assumption for the offset oscillator
Let f ref/M = 200 kHz and f offset = 98.0 MHz, then
Nmax =
118.6 98.0
= 103
0.2
and
Nmin =
98.8 98.0
=4
0.2
To program the LO such that the receiver tunes all FM stations

step N from 4, 5, 6, . . . , 102, 103
3-102
Example 3.21: Simple PLL Frequency Multiplication

A scheme for multiplication by three is shown below:
Input at fc
t
Hard limit
sinusoidal
input if
needed
Phase
Detector
Input Spectrum
Loop Filt.
& Ampl.
VCO
Centered at 3fc
xVCO = Acos[2(3fc)t]
fc
3fc
PLL as a Frequency Multiplier
3-103
Example 3.22: Simple PLL Frequency Division

A scheme for divide by two is shown below:
VCO Output
Phase
Detector
Input at fc
t
2T0
VCO Output Spectrum
Loop Filt.
& Ampl.
VCO
Centered at fc/2
Lowpass
Filter
Keep the
Fundamental
xLPF = Acos[2(fc/2)t]
fc/2
PLL as a Frequency Divider
3.4.3
Frequency-Compressive Feedback
xr(t)
ed(t)
BPF
eo(t)
x(t)
Discrim
VCO
ev(t)
Demod.
Output
Frequency compressive feedback PLL

3-104
If we place a discriminator inside the PLL loop a compressing

action occurs
Assume that
xr (t) = Ac cos[c t + (t)]
and
t
ev (t) = Av sin (c o )t + K v
ev () d
Then,
blocked by BPF
1
ed (t) = Ac Av sin (2c o )t + other terms
2
t
sin[o t + (t) K v
ev () d]
passed by BPF
so
1
x(t) = Ac Av sin o t + (t) K v
2
ev () d
Assuming an ideal discriminator
1
d(t)
ev (t) =
KD
K v ev (t)
2
dt
or
Kv K D
K D d(t)
ev (t) 1 +
=
2
2
dt
3-105
For FM d(t)/dt = 2 f d m(t), so

ev (t) =
K D fd
m(t)
1 + K v K D /(2)
which is the original modulation scaled by a constant

The discriminator input must be
1
1
x(t) = Ac Ad sin o t +
(t)
2
1 + K v K D /(2)
Assuming that K v K D /(2) 1 we conclude that the discriminator input has been converted to a narrowband FM signal,
which is justifies the name frequency compressive feedback
3.4.4
Coherent Carrier Recovery for DSB Demodulation
Recall that a DSB signal is of the form

xr (t) = m(t) cos c t
A PLL can be used to obtain a coherent carrier reference directly from xr (t)
Here we will consider the squaring loop and the Costas loop
3-106
m(t)cos(ct + )
xr(t)
LPF
Am2(t)cos(2ct + 2)
Loop
Filter
( )2
Bsin(2ct + 2)
cos(ct + )
VCO
static
phase
error
-90o
x2
m(t)cos()
0o
Squaring Loop
m(t)cos()
LPF
xr(t)
cos(ct + )
sin(ct + )
1 2
m (t)sin2
2
0o
Loop
Filter
ksin(2)
VCO
-90o
m(t)sin()
LPF
Costas Loop
Note: For both of the above loops m 2(t) must contain a DC

component
The Costas loop or a variation of it, is often used for carrier
recovery in digital modulation
Binary phase-shift keying (BPSK), for example, can be viewed
as DSB where
m(t) =
dn p(t nT )
n=
3-107
where dn = 1 represents random data bits and p(t) is a pulse

shaping function, say
1, 0 t T
p(t) =
0, otherwise
Note that in this case m 2(t) = 1, so there is a strong DC value
present
1
0.5
!0.5
!1
1
m(t)
10
t/T
m(t)cos(ct)
0.5
10
t/T
!0.5
!1
BPSK modulation
Digital signal processing techniques are particularly useful for

building PLLs
In the discrete-time domain, digital communication waveforms
are usually processed at complex baseband following some
form of I-Q demodulation
3-108
LPF
A/D
Sampling
fs clock
cos[2fcLt + L]
fs
xIF(t)
rI(t)
-90o
LPF
rQ(t)
A/D
DiscreteTime
r[n] = rI[n] + jrQ[n]
IF to discrete-time complex baseband conversion

y[n]
To Symbol Synch
x[n]
From
Matched
Filter
( )M 2M 2 1
j
[n]
e[n]
v[n] Error Generation
[n]
LUT
Im( )
z 1
kp
NCO
z 1
ka
Loop Filter
Mth-power digital PLL (DPLL) carrier phase tracking loop

From
Matched
Filter
L-Tap
Delay
x[n]
To Symbol Synch
y[n]
[n]
F( )
Rect.
to
Polar [n]
[n]
L-Tap
MA FIR
1
arg()
M
e j( )
e j( )
Non-Data Aided (NDA) feedforward carrier phase tracking

3-109
3.5
Sampling Theory
We now return to text Chapter 2, Section 8, for an introduction/review of sampling theory

Consider the representation of continuous-time signal x(t) by
the sampled waveform

x (t) = x(t)
(t nTs ) =
x(nTs )(t nTs )
n=
n=
x(t)
x(t)
Sampling
-Ts
Ts 2Ts 3Ts 4Ts 5Ts
How is Ts selected so that x(t) can be recovered from x (t)?

Uniform Sampling Theorem for Lowpass Signals
Given
then choose
F{x(t)} = X ( f ) = 0,
Ts <
1
2W
or
for f > W
f s > 2W
( f s = 1/Ts )
to reconstruct x(t) from x (t) and pass x (t) through an ideal

LPF with cutoff frequency W < B < f s W
2W = Nyquist frequency
f s /2 = folding frequency
3-110
proof:
X( f ) = X ( f )
fs
n=
( f n f s )
but X ( f ) ( f n f s ) = X ( f n f s ), so
X ( f ) = fs
n=
X(f)
X0
-W
Lowpass
reconstruction
filter
X ( f n fs )
Guard band
= fs - 2W
X(f)
X0 fs
...
...
fs > 2W
-fs
-W
-2fs
-fs
fs-W
fs
Aliasing
X0 fs
fs < 2W
...
...
0
fs
2fs
Spectra before and after sampling at rate f s
As long as f s W > W or f s > 2W there is no aliasing

(spectral overlap)
3-111
To recover x(t) from x (t) all we need to do is lowpass filter

the sampled signal with an ideal lowpass filter having cutoff
frequency W < f cutoff < f s W
In simple terms we set the lowpass bandwidth to the folding
frequency, f s /2
Suppose the reconstruction filter is of the form

f
H ( f ) = H0
e j2 f t0
2B
we then choose W < B < f s W
For input X ( f ), the output spectrum is
Y ( f ) = f s H0 X ( f )e j2 f t0
and in the time domain
y(t) = f s H0 x(t t0)
If the reconstruction filter is not ideal we then have to design
the filter in such a way that minimal desired signal energy is removed, yet also minimizing the contributions from the spectral
translates either side of the n = 0 translate
The reconstruction operation can also be viewed as interpolating signal values between the available sample values
Suppose that the reconstruction filter has impulse response h(t),
3-112
then
y(t) =
n=
x(nTs )h(t nTs )
= 2B H0
n=
x(nTs )sinc[2B(t t0 nTs )]
where in the last lines we invoked the ideal filter described

earlier
Uniform Sampling Theorem for Bandpass Signals
If x(t) has a single-sided bandwidth of W Hz and
F{x(t)} = 0
for
f > fu
then we may choose
2 fu
m
where

fu
m=
,
W
which is the greatest integer less than or equal to f u /W
fs =
Example 3.23: Bandpass signal sampling

1
0.8
0.6
0.4
0.2
!4
!2
X(f)
Input signal spectrum

3-113
In the above signal spectrum we see that

W = 2,
fu = 4
f u /W = 2 m = 2
so
fs =
will work
2(4)
=4
2
The sampled signal spectrum is

X( f ) = 4
Recover with
bandpass filter
4
3
2
1
!15
-3fs
!10
-2fs
!5
-fs
n=
X ( f n fs )
X(f)
fs
2fs
10
3fs
15
Spectrum after sampling
3-114
3.6. ANALOG PULSE MODULATION
3.6
Analog Pulse Modulation
The message signal m(t) is sampled at rate f s = 1/Ts

A characteristic of the transmitted pulse is made to vary in a
one-to-one correspondence with samples of the message signal
A digital variation is to allow the pulse attribute to take on
values from a finite set of allowable values
3.6.1
Pulse-Amplitude Modulation (PAM)
PAM produces a sequence of flat-topped pulses whose amplitude varies in proportion to samples of the message signal
Start with a message signal, m(t), that has been uniformly sampled
m (t) =
m(nTs )(t nTs )
n=
The PAM signal is
t (nTs + /2)
m c (t) =
m(nTs )
n=
m(t)
mc(t)
Ts
2Ts
3Ts
4Ts
PAM waveform
3-115
It is possible to create m c (t) directly from m (t) using a zeroorder hold filter, which has impulse response
t /2
h(t) =
and frequency response
H ( f ) = sinc( f )e j f
m(t)
mc(t)
h(t)
How does h(t) change the recovery operation from the case of
ideal sampling?
If Ts we can get by with just a lowpass reconstruction filter having cutoff frequency at f s /2 = 2/Ts
In general, there may be a need for equalization if tau is
on the order of Ts /4 to Ts /2
Lowpass
reconstruction
filter
sinc() function
envelope
-fs
mc(t)
-W
Lowpass
fs
m(t)
Recovery of m(t) from m c (t)

3-116
3.6. ANALOG PULSE MODULATION
3.6.2
Pulse-Width Modulation (PWM)
A PWM waveform consists of pulses with width proportional

to the sampled analog waveform
For bipolar m(t) signals we may choose a pulse width of Ts /2
to correspond to m(t) = 0
The biggest application for PWM is in motor control
It is also used in class D audio power amplifiers
A lowpass filter applied to a PWM waveform recovers the
modulation m(t)
PWM Signal
1
0.5
!20
!10
Analog input m(t)
!0.5
!1
10
20
Example PWM signal
3.6.3
Pulse-Position Modulation
With PPM the displacement in time of each pulse, with respect to a reference time, is proportional to the sampled analog
waveform
The time axis may be slotted into a discrete number of pulse
positions, then m(t) would be quantized
Digital modulation that employs M slots, using nonoverlapping pulses, is a form of M-ary orthogonal communications
3-117
PPM of this type is finding application in ultra-wideband

communications
PPMSignal
1
0.5
!20
!10
Analog input m(t)
10
!0.5
!1
20
Example PPM signal
3.7
Delta Modulation and PCM
This section considers two pure digital pulse modulation schemes

Pure digital means that the output of the modulator is a binary
waveform taking on only discrete values
3.7.1
Delta Modulation (DM)
The message signal m(t) is encoded into a binary sequence

which corresponds to changes in m(t) relative to reference
waveform m s (t)
DM gets its name from the fact that only the difference from
sample-to-sample is encoded
The sampling rate in combination with the step size are the two
primary controlling modulator design parameters
3-118
3.7. DELTA MODULATION AND PCM
m(t)
d(t)
xc(t)
(t)
-1
Pulse Modulator
ms(t) =
Control the
step size
Delta modulator with step size parameter 0

Start-up transient
m(t) and ms(t)
m(t) (blue)
ms(t) (red)
0 = 0.15
0.5
0
Slope
overload
0.5
1
0
0.005
0.01
0.015
0.02
0.025 0.03
Time (s)
0.035
0.04
0.045
0.05
0.005
0.01
0.015
0.02
0.025 0.03
Time (s)
0.035
0.04
0.045
0.05
1
xc(t)
0.5
0
0.5
1
Delta modulator waveforms
The maximum slope that can be followed is 0/Ts

3-119
A MATLAB DM simulation function is given below

function [t_o,x,ms] = DeltaMod(m,fs,delta_0,L)
% [t,x,ms] = DeltaMod(m,fs,delta_0,L)
%
n = 0:(L*length(m))-1;
t_o = n/(L*fs);
ms = zeros(size(m));
x = zeros(size(m));
ms_old = 0; % zero initial condition
for k=1:length(m)
x(k) = sign(m(k) - ms_old);
ms(k) = ms_old + x(k)*delta_0;
ms_old = ms(k);
end
x = [x; zeros(L-1,length(m))];
x = reshape(x,1,L*length(m));
The message m(t) can be recovered from xc (t) by integrating

and then lowpass filter to remove the stair step edges (lowpass
filtering directly is a simplification)
Slope overload can be dealt with through an adaptive scheme
If m(t) is nearly constant keep the step size 0 small
If m(t) has large variations, a larger step size is needed
With adaptive DM the step size is controlled via a variable gain
amplifier, where the gain is controlled by square-law detecting
the output of a lowpass filter acting on xc (t)
3-120
m(t)
d(t)
ms(t)
xc(t)
(t)
-1
Pulse Modulator
VGA
( )2
LPF
Means to obtain a variable step size DM
3.7.2
Pulse-Code Modulation (PCM)
Each sample of m(t) is mapped to a binary word by

1. Sampling
2. Quantizing
3. Encoding
m(t)
Equivalent
Views
m(t)
Sampler
Quantizer
Sample
&
Hold
Analog to
Digital
Converter n
Encoder
PCM
Output
Parallel
to Serial
Converter
Serial
Data
3-121
Quant. Encoded
Level
Output
7
111
6
110
5
101
4
100
3
011
2
010
1
001
0
000
0
Quantizer Bits: n = 3, q = 2n = 8
m(t)
Ts
2Ts
3Ts
4Ts
5Ts
6Ts
7Ts
Encoded Serial PCM Data: 001 100 110 111 110 100 010 010 ...
3-Bit PCM encoding
Assume that m(t) has bandwidth W Hz, then

Choose f s > 2W
Choose n bits per sample (q = 2n quantization levels)
2nW binary digits per second must be transmitted

Each pulse has width no more than
1
,
2nW
so using the fact that the lowpass bandwidth of a single pulse
is about 1/(2 ) Hz, we have that the lowpass transmission
bandwidth for PCM is approximately
( )max =
B kW n
where k is a proportionality constant
When located on a carrier the required bandwidth is doubled
3-122
Binary phase-shift keying (BPSK), mentioned earlier, is a popular scheme for transmitting PCM using an RF carrier
Many other digital modulation schemes are possible
The number of quantization levels, q = log2 n, controls the
quantization error, assuming m(t) lies within the full-scale range
of the quantizer
Increasing q reduces the quantization error, but also increases
the transmission bandwidth
The error between m(kTs ) and the quantized value Q[m(kTs )],
denoted e(n), is the quantization error
If n = 16, for example, the ratio of signal power in the samples
of m(t), to noise power in e(n), is about 95 dB (assuming m(t)
stays within the quantizer dynamic range)
Example 3.24: Compact Disk Digital Audio

CD audio quality audio is obtained by sampling a stereo source
at 44.1 kHz
PCM digitizing produces 16 bits per sample per L/R audio
channel
3-123
0.163 mm
One Frame of 12 Audio Samples

Synch Sub
(27 bits) Code
(8 bits)
Data (96 bits)
Parity
(32 bits)
Data (96 bits)
Parity
(32 bits)
CD recoding frame format
The source bit rate is thus 2 16 44.1ksps = 1.4112 Msps

Data framing and error protection bits are added to bring the
total bit count per frame to 588 bits and a serial bit rate of
4.3218 Mbps
3.8
Multiplexing
It is quite common to have multiple information sources located at the same point within a communication system
To simultaneously transmit these signals we need to use some
form of multiplexing
3-124
3.8. MULTIPLEXING
There is more than one form of multiplexing available to the

communications engineer
3.8.1
Frequency-Division Multiplexing (FDM)
With FDM the idea is to locate a group of messages on different subcarriers and then sum then together to form a new
baseband signal which can then be modulated onto the carrier
m1(t)
Mod
#1
Lower bound on the

composite signal bandwidth
fsc1
m2(t)
Mod
#2
RF
Mod
fsc2
fc
...
Composite
baseband
mN(t)
Mod
#N
xc(t)
fscN
FDM transmitter
At the receiver we first demodulate the composite signal, then

separate into subcarrier channels using bandpass filters, then
demodulate the messages from each subcarrier
3-125
RF
Demod
BPF
fsc1
Sub Car.
Demod #1
yD1(t)
BPF
fsc2
Sub Car.
Demod #2
yD2(t)
...
...
...
BPF
fscN
Sub Car.
Demod #N
yDN(t)
FDM receiver/demodulator
The best spectral efficiency is obtained with SSB subcarrier

modulation and no guard bands
At one time this was the dominant means of routing calls in the
public switched telephone network (PSTN)
In some applications the subcarrier modulation may be combinations both analog and digital schemes
The analog schemes may be combinations of amplitude modulation (AM/DSM/SSB) and angle modulation (FM/PM)
3-126
3.8. MULTIPLEXING
Example 3.25: FM Stereo

l(t) + r(t)
l(t)
+
+
r(t)
l(t) - r(t)
xb(t)
+
x2
Freq. Mult
19 kHz
Pilot
38 kHz
19 kHz
pilot
Pilot
Carrier
Xb(f)
15
19
FM
Mod
xc(t)
fc
Other subcarrier
services can occupy
this region
23
38
53
f (kHz)
FM stereo transmitter
xr(t)
FM
Discrim
xb(t)
BPF
fc = 19
kHz
x 2 Freq
Mult
LPF
W = 15
kHz
LPF
W = 15
kHz
Mono
output
l(t) + r(t)
l(t)
l(t) - r(t)
r(t)
Coherent demod
of DSB on 38
kHz subcarrier
FM stereo receiver
3-127
3.8.2
Quadrature Multiplexing (QM)

Accosct
2cosct
xc(t)
m2(t)
Acsinct
Channel
m1(t)
xr(t)
d1(t)
d2(t)
LPF
yD1(t)
LPF
yD2(t)
2sinct
QM modulation and demodulation
With QM quadrature (sin/cos) carrier are used to send independent message sources
The transmitted signal is
xc (t) = Ac m 1(t) cos c t + m 2(t) sin c t
If we assume an imperfect reference at the receiver, i.e., 2 cos(c t+

), we have
d1(t) = Ac m 1(t) cos m 2(t) sin
+ m 1(t) cos(2c t + ) + m 2(t) sin(2c t + )
LPF removes these terms
y D1(t) = Ac m 1(t) cos + m 2(t) sin

The second term in y D1(t) is termed crosstalk, and is due to
the static phase error
3-128
3.8. MULTIPLEXING
Similarly
y D2(t) = Ac m 2(t) cos m 1(t) sin

Note that QM acheives a bandwidth efficiency similar to that
of SSB using adjacent two subcarriers or USSB and LSSB together on the same subcarrier
3.8.3
Time-Division Multiplexing (TDM)
Time division multiplexing can be applied to sampled analog

signals directly or accomplished at the bit level
We assume that all sources are sample at or above the Nyquist
rate
Both schemes are similar in that the bandwidth or data rate of
the sources being combined needs to be taken into account to
properly maintain real-time information flow from the source
to user
For message sources with harmonically related bandwidths we
can interleave samples such that the wideband sources are sampled more often
To begin with consider equal bandwidth sources
3-129
Info.
Source 1
Info.
Source 2
Synchronization
Required
Info.
User 2
Channel
...
...
Info.
Source N
Info.
User 1
Commutators
Info.
User N
For equal bandwidth: s1s2s3 s1s2s3 s1s2s3 s1s2s3 s1s2s3 s1s2s3 s1s2s3 ....
Analog TDM (equal bandwidth sources)
Suppose that m 1(t) has bandwidth 3W and sources m 2(t), m 3(t),

and m 4(t) each have bandwidth W , we could send the samples
as
s1 s2 s1 s3 s1 s4 s1 s2 s1 . . .
with the commutator rate being f s > 2W Hz
The equivalent transmission bandwidth for multiplexed signals
can be obtained as follows
Each channel requires greater than 2Wi samples/s
The total number of samples, n s , over N channels in T s
is thus
N
ns =
2Wi T
i=1
An equivalent signal channel of bandwidth B would produce 2BT = n s samples in T s, thus the equivalent base3-130
3.8. MULTIPLEXING
band signal bandwidth is

B=
Wi Hz
i=1
which is the same minimum bandwidth required for FDM

using SSB
Pure digital multiplexing behaves similarly to analog multiplexing, except now the number of bits per sample, which
takes into account the sample precision, must be included
The earlier PCM example for CD audio this was taken
into account when we said that left and right audio channels each sampled at 44.1 ksps with 16-bit quantizers,
multiplex up to
2 16 44, 100 = 1.4112 Msps
3-131
Example 3.26: Digital Telephone System

The North American digital TDM hierarchy is based on single
voice signal sampled at 8000 samples per second using an 7-bit
quantizer plus one signaling bit
The serial bit-rate per voice channel is 64 kbps
North American Digital TDM Hierarchy)
Digital
No. of 64 kbps
Signal
Bit Rate
PCM VF
Sys. Number R (Mb/s)
Channels
DS-0
0.064
1
T1 DS-1
1.544
24
T1C DS-1C
3.152
48
T2 DS-2
6.312
96
T3 DS-3
44.736
672
DS-3C
90.254
1344
DS-4E
139.264
2016
T4 DS-4
274.176
4032
DS-432
432.00
6048
T5 DS-5
560.160
8064
Transmission
Media Used
Wire pairs
Wire pairs
Wire pairs
Wire pairs
Coax, radio, fiber
Radio, fiber
Radio, fiber, coax
Coax, fiber
Fiber
Coax, fiber
Consider the T1 channel which contains 24 voice signals

Eight total bits are sent per voice channel at a sampling rate of
8000 Hz
The 24 channels are multiplexed into a T1 frame with an extra
bit for frame synchronization, thus there are 24 8 + 1 = 193
bits per frame
3-132
3.9. GENERAL PERFORMANCE OF MODULATION SYSTEMS IN NOISE
Frame period is 1/8000 = 0.125 ms, so the serial bit rate is

193 8000 = 1.544 Mbps
Four T1 channels are multiplexed into a T2 channel (96 voice
channels)
Seven T2 channels are multiplexed into a T3 channel (672
voice channels)
Six T3 channels are multiplexed into a T4 channel (4032 voice
channels)
3.9
General Performance of Modulation

Systems in Noise
Regardless of the modulation scheme, the received signal xr (t),

is generally perturbed by additive noise of some sort, i.e.,
xr (t) = xc (t) + n(t)
where n(t) is a noise process
The pre- and post-detection signal-to-noise ratio (SNR) is used
a figure or merit
3-133
xr(t)
Pre-Det.
Filter
Demod/
Detector
P
(SNR)T = T
<n2(t)>
yD(t)
(SNR)D =
Common to
all systems
(SNR)D
PCM
q = 256
PCM
q = 64
FM
FM
,D
1
D=
=
,D
FM
=2
<m2(t)>
<n2(t)>
5
Nonlinear modulation systems
have a distinct
threshold in noise
B
DS
Q
B, mod
S
S
e
B, nt D
S
D ere
h
Co
(SNR)T
General modulation performance in noise
3-134
Appendix
Physical Noise Sources

Contents
A.1 Physical Noise Sources . . . . . . . . . . . . . . . . . . A-3
A.1.1 Thermal Noise . . . . . . . . . . . . . . . . . . A-4
A.1.2 Nyquists Formula . . . . . . . . . . . . . . . . A-6
A.1.3 Shot Noise . . . . . . . . . . . . . . . . . . . . A-11
A.1.4 Other Noise Sources . . . . . . . . . . . . . . . A-12
A.1.5 Available Power . . . . . . . . . . . . . . . . . A-13
A.1.6 Frequency Dependence . . . . . . . . . . . . . . A-15
A.1.7 Quantum Noise . . . . . . . . . . . . . . . . . . A-15
A.2 Characterization of Noise in Systems . . . . . . . . . A-16
A.2.1 Noise Figure of a System . . . . . . . . . . . . . A-16
A.2.2 Measurement of Noise Figure . . . . . . . . . . A-18
A.2.3 Noise Temperature . . . . . . . . . . . . . . . . A-20
A.2.4 Effective Noise Temperature . . . . . . . . . . . A-21
A.2.5 Cascade of Subsystems . . . . . . . . . . . . . . A-22
A.2.6 Attenuator Noise Temperature and Noise Figure
A-23
A.3 Free-Space Propagation Channel . . . . . . . . . . . . A-28
A-1
APPENDIX A. PHYSICAL NOISE SOURCES
A-2
A.1. PHYSICAL NOISE SOURCES
A.1
Physical Noise Sources
In communication systems noise can come from both internal

and external sources
Internal noise sources include
Active electronic devices such as amplifiers and oscillators
Passive circuitry
Internal noise is primarily due to the random motion of charge
carriers within devices and circuits
The focus of this chapter is modeling and analysis associated
with internal noise sources
External sources include
Atmospheric, solar, and cosmic noise
Man-made sources such as intentional or unintentional
jamming
To analyze system performance due to external noise location
can be very important
Understanding the impact on system performance will require
on-site measurements
A-3
A.1.1
Thermal Noise
Thermal noise is due to the random motion of charge carriers

Nyquists Theorem: States that the noise voltage across a resistor is
2
v rms
= v n2(t) = 4kT R B v2
where
k
T
R
B
= Boltzmanns constant = 1.38 1023 J/K

= Temperature in Kelvin
= resistance in ohms
= measurement bandwidth
R
vrms = (4KTRB)1/2
irms = (4KTGB)1/2
noiseless
G = 1/R
noiseless
Equivalent noise circuits: voltage and current
A-4
Consider the following resistor network

R2
R1
R3
v22
R1
R2
vi2 = 4KTRiB
i = 1, 2, 3
v12
vo
R3
vo
v32
Noise analysis for a resistor network
Since the noise sources are independent, the total noise voltage, v o can be found by summing the square of the voltage due
to each noise source (powers due to independent sources add)
2
2
2
v o2 = v o1
+ v o2
+ v o3
The noise voltages, v o1, v o2, v o3, can be found using superposition
A-5
A.1.2
Nyquists Formula
R, L, C
Network
vrms
Z(f)
Nyquists formula for passive networks
Consider a one-port R, L , C network with input impedance in

the frequency domain given by Z ( f )
Nyquists theorem states that
2
v rms
where
v n2
= 2kT
R( f ) d f
R( f ) = Re Z ( f )
For a pure resistor network Nyquists formula reduces to

B
v n2 = 2kT
Req d f = 4kT Req B
B
In the previous example involving three resistors

Req = R3||(R1 + R2)
Example A.1: Circuit simulation for noise characterization

Spice and Spice-like circuit simulators, e.g. Qucs, have the
ability to perform noise analysis on circuit models
A-6
The analysis is included as part of an AC simulation (in Qucs

for example it is turned off by default)
When passive components are involved the analysis follows
from Nyquists formula
The voltage that AC noise analysis returns is of the form
v rms
= 4kT R( f )
Hz
where the B value has been moved to the left side, making the
noise voltage a spectral density like quantity
When active components are involved more modeling information is required
Consider the following resistor circuit
measure vrms here
T = 300oK
Req
Pure resistor circuit

A-7
To apply Nyquists formula we need Req

Req = 100K||(10 + 5 + 20)K
100 35
=
K = 25.93 K
100 + 35
In Nyquists formula the rms noise voltage normalized by B is
v rms
= 4kT 25.93 103
Hz
8
= 2.072 10 v/ Hz
assuming T = 300 K
Circuit simulation results are shown below
Resistor circuit RMS noise voltage (v rms / Hz)
Circuit simulation becomes particularly useful when reactive

elements are included
A-8
To demonstrate this we modify the resistor circuit by placing a

10 nf capacitor in shunt with the 5 K resistor
vrms
T = 300oK
v rms / Hz for a simple passive RC circuit
The input impedance of this circuit is
R4 C1 s
1
+ R2 + R5 R3
R4 + C1 s
1
Z (s) =
1
R4 C s
1
+ R2 + R5 + R3
R + 1
4
C1 s
Here the noise voltage/v rms/ Hz takes on two limiting values

depending upon whether the capacitor acts as an open circuit
or a short circuit
To get the actual rms noise voltage as
measured by an AC voltmeter, we need to integrate the vrms/ Hz quantity, which can
be accomplished with a true rms measuring instrument

2
v rms
= 4kT
Re{Z ( f )} d f
0
A-9
Example A.2: Active circuit modeling

For Op-Amp based circuits noise model information is usually
available from the data sheet1
Circuit simulators include noise voltage and current sources
just for this purpose
741 Noise Data
Op Amp Noise Model
inn
inp
en
Noiseless
Op Amp
Op amp noise model with 741 data sheet noise information
Consider an inverting amplifier with a gain of 10 using a 741

op-amp
This classic op amp, has about a 1MHz gain-bandwidth product, so with a gain of 10, the 3 dB cutoff frequency of the
amplifier is at about 100 kHz
The noise roll-off is at the same frequency
1 Ron
Mancini, editor, Op Amps for Everyone: Design Reference, Texas Instruments Advanced
Analog Products, Literature number SLOD006, September 2000.
A-10
The rms noise as v/ Hz plotted below, is a function of the

op amp noise model and the resistors used to configure the
amplifier gain
With relatively low impedance configured at the inputs to the
op amp, the noise voltage en dominates, allowing the noise
currents to be neglected
vrms
741
T = 300oK
Gain = 10 so fc is at
about 100 kHz
Noise voltage at the op amp output
A.1.3
Shot Noise
Due to the discrete nature of current flow in electronic devices

Given an average current flow of Id A,
2
i rms
= i n2(t) = 2eId B A2
where e = 1.6 1019 is the charge on an electron

A-11
Special Case: For a PN junction diode
eV
I = Is exp
1 A
kT
where Is is the reverse saturation current
Assuming Is and Is exp(eV /kT ) to be independent sources in
terms of noise sources, then
eV
2
i rms,tot
= 2eIs exp
+ 2eIs B
kT
= 2e I + Is B A2
For I Is the diode differential conductance is
go =
dI
eI
=
,
dV
kT
thus
i rms,tot 2eI B = 2kT go B
which is half the noise due to a pure resistance
A.1.4
Other Noise Sources
Generation-Recombination Noise: Results from generated free

carriers recombining in a semiconductor (like shot noise)
Temperature-Fluctuation Noise: Results from fluctuating heat
exchange between devices and the environment
Flicker Noise: Has a spectral density of the form 1/ f 1/ f ,
also known as pink noise; the physics is not well understood
A-12
A.1.5
Available Power
R
vrms
RL = R
irms
(a)
GL = G
(b)
Noise analysis is often focused around receiver circuitry where

maximum power transfer is implemented, i.e., match the load
and sources resistances
Under these conditions the power delivered to the load is the
available power Pa
2
1
2
i
2 rms
i rms
(a) Pa =
=
R
4R
2
1
2
i
2 rms
i rms
b Pa =
=
G
4G
For a noisy resistor
2
v rms
= 4kT R B,
so
Pa,R =
4kT R B
= kT B W
4R
A-13
Example A.3: Fundamental Example

Consider room temperature to be To = 290 K, then the thermal
noise power density is
Pa,R
= 4.002 1021 W/Hz
B
For communication system analysis a popular measurement
unit for both signal and nois epower levels, is the power ratio in decibels (dB) referenced to
(i)
1 W 0 dBW
= 10 log10
(ii)
1 mW 0dBm
= 10 log10
PWatts
; PWatt = 1
1 Watt
PmW
; PmW = 1 mW
1 mW
In dB units thermal noise power spectral density under maximum power transfer is
4.002 1021
Pwr/Hz (dBW) = 10 log10
204 dBW/Hz
1W
4.002 1021
Pwr/Hz (dBm) = 10 log10
174 dBm/Hz
1 mW
A-14
A.1.6
Frequency Dependence
If frequency dependence is included, then the available power

spectral density is
Sa ( f ) =
where
hf
Pa

=
W/Hz
hf
B
exp kT 1
h = Plancks constant = 6.6254 1034 J-sec

Noise Spectrum (dBM)
-170
-175
-180
-185
-190
-195
hf
290 K
29 K
2.9 K
-200
-205
10
100
1000
10000
f (GHz)
100000.
Infrared
Thermal noise spectral density, including quantum noise
A.1.7
Quantum Noise
To account for quantum noise the term h f must be added

Thermal noise dominates for most applications (i.e., < 20 GHz),
except in optical systems and some millimeter wave systems
A-15
A.2
Characterization of Noise in Systems
In communication system modeling we wish to consider how

the noise introduced by each subsystem enters into the overall
noise level delivered to the demodulator
In RF/microwave systems the concept of representing a system
as a cascade of subsystems is particularly appropriate, since all
connections between subsystems is done at a constant impedance
level of say 50 ohms
R0
)NS )
Subsys
1
)NS )
Subsys
2
)NS )
)NS )
Subsys
N
)NS )
N-1
N -subsystem cascade analysis
A.2.1
Noise Figure of a System

Rl-1, Ts
es,l-1
es,l
Subsys
l
Rl
lth subsystem model
For the lth subsystem define the noise figure, Fl , as

S
1 S
=
N l
Fl N l1
A-16
A.2. CHARACTERIZATION OF NOISE IN SYSTEMS
Ideally, Fl = 1, in practice Fl > 1, meaning that each subsystems generates some noise of its own
In dB the noise figure (NF) is
FdB = 10 log10 Fl
Assuming the subsystem input and put impedances (resistances)

are matched, then our analysis may be done in terms of the
available signal power and available noise power
For the lth subsystem the available signal power at the input is
Psa,l1 =
2
es,l1
4Rl1
Assuming thermal noise only, the available noise power is

Pna,l1 = kTs B
where Ts denotes the source temperature

Assuming that the lth subsystem (device) has power gain G a ,
it follows that
Psa,l = G a Psa,l1
where we have also assumed the system is linear
We can now write that

S
Psa,l
1 Psa,l1
1 S
=
=
=
N l
Pna,l
Fl Pna,l1
Fl N l1
which implies that
Fl =
Psa,l1
Pna,l
Pna,l
=
Pna,l1
Psa,l
G a Pna,l1

G a Psa,l1
kTs B
A-17
Now
Pna,l = G a Pna,l1 + Pint,l
where Pint,l is internally generated noise

Finally we can write that
Pint,l
G a kTs B
Note that if G a 1 Fl 1, assuming that G a is
independent of Pint,l
Fl = 1 +
As a standard, NF is normally given with Ts = T0 = 290 K, so

Fl = 1 +
A.2.2
Pint,l
G a kT0 B
Measurement of Noise Figure
In practice NF is measured using one or two calibrated noise

sources
Method #1
A source can be constructed using a saturated diode which produces noise current
in2 = 2eId B A2
The current passing through the diode is adjusted until the
noise power at the output of the devide under test (DUT) is
double the amount obtained without the diode, then we obtain
eId Rs
F=
2kT0
A-18
where Rs is the diode series resistance and Id is the diode current

Method #2
The so-called Y -factor method requires hot; and cold calibrated noise sources and a precision variable attenuator
Noise
Source
Thot
Device
Under Test
Te, G, B
Noise
Source
Tcold
Calibrated
Attenuator
Power
Meter
Y factor determination of NF
From noise power measurements taken with the hot and cold
sources we form the ratio
Ph
k(Thot + Te )BG
Thot + Te
=Y =
=
Pc
k(Tcold + Te )BG
Tcold + Te
Solving for Te
Te =
Thot Y Tcold
Y 1
The Y value is obtained by noting the attenuator setting change,

A dB, needed to maintain Pc = Ph and calculating Y =
10A/10
A-19
A.2.3
Noise Temperature
The equivalent noise temperature of a subsystem/device, is defined as

Pn,max
Tn =
kB
with Pn,max being the maximum noise power of the source into
bandwidth B
Example A.4: Resistors in series and parallel

Find Tn for two resistors in series
R2, T2
R2 + R1
vn
R1, T1
and
therefore
v n2 = 4k B R1 T1 + 4k B R2 T2
v n2
4k(T1 R1 + T2 R2)B
Pna =
=
4(R1 + R2)
4(R1 + R2)
Tn =
Pna
T1 R1 + T2 R2
=
kB
R1 + R2
Find Tn for two resistors in parallel

R1, T1
A-20
R2, T2
in
R1 || R2 = G1 + G2
i n2 = 4k BG 1 T1 + 4k BG 2 T2
and
therefore
i n2
4k(T1 G 1 + T2 G 2)B
Pna =
=
4(G 1 + G 2)
4(G 1 + G 2)
Tn =
A.2.4
T1 R2 + T2 R1
T1 G 1 + T2 G 2
=
G1 + G2
R1 + R2
Effective Noise Temperature
Recall the expression for NF at stage l

Fl = 1 +
Pint,l
Te
=1+
G kT B
T0
a 0
internal noise
Note: Pint,l /(G a k B) has dimensions of temperature

Define
Pint,l
= effective noise temp.,
Gak B
which is a measure of the system noisiness
Te =
Next we use Te to determine the noise power at the output of

the lth subsystem
Recall that
Pna,l = G a Pna,l1 + Pint,l
= G a kTs B + G a kTe B
= G a k(Ts + Te )B
A-21
This references all of the noise to the subsystem input by virtue

of the G a term
A.2.5
Cascade of Subsystems
Consider two systems in cascade and the resulting output noise

contributions
Ts
The noise here

is due to the
following
1. Amplified source noise = G a1 G a2 kTs B
2. Internal noise from amplifier 1 = G a1 G a2 kTe1 B

3. Internal noise from amplifier 2 = G a2 kTe2 B
Thus
Te
Pna,2 = G a1 G a2 k Ts + Te1 + 2
G a1
which implies that
Te = Te1 +
Te2
G a1
and since F = 1 + Te /T0
Te1
Te2
F =1+
+
T0
G a1 T0
= F1 +
1+
Te2
T0
G a1
F2 1
= F1 +
G a1
A-22
In general for an arbitrary number of stages (Friis formula

F3 1
F2 1
+
+
G a1
G a1 G a2
Te
Te3
Te = Te1 + 2 +
+
G a1 G a1 G a2
F = F1 +
A.2.6
Attenuator Noise Temperature and Noise

Figure
Atten
L
Ts
Pa,out =
Pa,in
L
Resistive network at
temperature Ts
Attenuator model
Since the attenuator is resistive, we know that the impedances

are matched and
Pna,out = kTs B (independent of Rs or L)
Let the equivalent temperature of the attenuator be Te , then
Pna,out = G a k(Ts + Te )B
1
= k(Ts + Te )B
L
looks like Pan,in
also
Thus since Pan,out = kTs B, it follows that

1
(Ts + Te ) = Ts
L
A-23
or
Te = (1 L)Ts
Now since
F =1+
Te
(L 1)Ts
=1+
T0
T0
with Ts = T0 (i.e., attenuator at room temperature)

Fattn = 1 + L 1 = L
Example A.5: 6 dB attenuator

The attenuator analysis means that a 6 dB attenuator has a
noise figure of 6 dB
Example A.6: Receiver system
Attn
RF
Amplifier
Feedline
Loss
L = 1.5 dB
G2 = 20 dB
F1 = 1.5 dB F2 = 7 dB
Mixer
IF
Amplifier
G3 = 8 dB
F3 = 10 dB
G4 = 60 dB
F4 = 6 dB
Receiver front-end
A-24
We need to convert from dB back to ratios to use Friis formula

G1
G2
G3
G4
1
= 101.5/10 = 1.41
= 1020/10 = 100
= 108/10 = 6.3
= 1060/10 = 106
F1
F2
F3
F4
= 101.5/10 = 1.41
= 107/10 = 5.01,
= 10
= 3.98
The system NF is
5.01 1
10 1
3.98 1
+
+
1/1.41
100/1.41 (100)(6.3)/1.41
= 7.19 or 8.57 dB
F = 1.41 +
The effective noise temperature is

Te = T0(F 1) = 290(7.19 1)
= 1796.3 K
To reduce the noise figure (i.e., to improve system performance)
interchange the cable and RF preamp
In practice this may mean locating an RF preamp on the back
of the receive antenna, as in a satellite TV receiver
With the system of this example,
1.41 1
10 1
3.98 1
+
+
100
100/1.41 (100)(6.3)/1.41
= 5.15 or 7.12 dB
Te = 1202.9 K
F = 5.01 +
Note: If the first component has a high gain then its noise figure
dominates in the cascade connection
A-25
Note: The antenna noise temperature has been omitted, but

could be very important
Example A.7: Receiver system with antenna noise temperature
Ts = 400 K
Attn
RF
Amplifier
Feedline
Loss
L = 1.5 dB
G2 = 20 dB
F1 = 1.5 dB F2 = 7 dB
Mixer
IF
Amplifier
G3 = 8 dB
F3 = 10 dB
G4 = 60 dB
F4 = 6 dB
F = 7.19 or FdB = 8.57 dB, Te = 1796.3 K
Rework the previous example, except now we calculate available noise power and signal power with additional assumptions
about the receiving antenna
Suppose the antenna has an effective noise temperature of Ts =
400 K and the system bandwidth is B = 100 kHz
What is the maximum available output noise power in dBm?
Since
Ts + Te
Pna = G a k(Ts + Te )B = (G a )(kT0)
(B)
T0
A-26
where
G a,dB = 1.5 + 20 + 8 + 60 = 86.5 dB
kT0 = 174 dBm/Hz, T0 = 290 K
we can write in dB that
Pna,dB
400 + 1796.3
= 86.5 174 + 10 log
+ 10 log10 105
290
= 28.71 dBm
What must the received signal power at the antenna terminals

be for a system output SNR of 20 dB?
Let the received power be Ps or in dBm Ps,dB
G a Ps
10 log10
= 20
Pna
Solving for Ps in dbm
Ps,dB = 20 + Pna,dB G a , dB
= 20 + (28.71) 86.5 = 95.21 dBm
A-27
A.3
Free-Space Propagation Channel
A practical application of the noise analysis is in calculating

the link budget for a free-space communications link
This sort of analysis applies to satellite communications
Relay
Satellite
Downlink
Uplink
Ground
Station
Rec.
User
Earth
Satellite link scenario
Consider an isotropic radiator which is an ideal omnidirectional antenna
Power density
at distance d
from the
transmitter
Power PT is radiated uniformly

in all directions (a point source)
Omni antenna and received flux density
The power density at distance d from the source (antenna) is

PT
2
pt =
W/m
4d 2
A-28
A.3. FREE-SPACE PROPAGATION CHANNEL
An antenna with directivity (more power radiated in a particular direction), is described by a power gain, G T , over an
isotropic antenna
For an aperture-type antenna, e.g., a parabolic dish antenna,
with aperture area, A T , such that
A T 2
with the transmit wavelength, G T is given by
GT =
4 A T
2
Assuming a receiver antenna with aperture area, A R , it follows

that the received power is
PT G T
Ar
4 d 2
PT G T G R 2
=
(4 d)2
PR = pt A R =
since A R = G R 2/(4)
For system analysis purposes modify the PR expression to include a fudge factor called the system loss factor, L 0, then we
can write
2 PT G T G R
PR =
4 d
L0

Free space loss
A-29
In dB (actually dBW or dBm) we have

PR,dB = 10 log10 PR
= 20 log10
4 d
+ 10 log10 PT + 10 log10 G T
EIRP
+ 10 log10 G R 10 log10 L 0
where EIRP denotes the effective isotropic radiated power
Example A.8: Free-Space Propagation

Consider a free-space link (satellite communications) where
Trans. EIRP = (28 + 10) = 38 dBW
Trans. Freq = 400 MHz
The receiver parameters are:
Rec. noise temp. = Ts + Te = 1000 K
Rec. ant. gain = 0 dB
Rec. system loss L 0) = 3 dB
Rec. bandwidth = 2 kHz
Path length d = 41, 000 Km
Find the output SNR in the 2 kHz receiver bandwidth
A-30
A.3. FREE-SPACE PROPAGATION CHANNEL
The received signal power is
3 108/4 108
PR,dB = 20 log10
+ 38 dBW + 0 3
4 41, 000 103
= 176.74 + 38 3 = 141.74 dBW
= 111.74 dBm
Note: = c/ f = 3 108/400 106
The receiver output noise power is
Pna,dB = 10 log10(kT0) + 10 log10
= 174 + 5.38 + 33
= 135.62 dBm
Hence
SNRo, dB
Te
+ 10 log10 B
T0
PR
= 10 log10
Pna
= 111.74 (135.62)
= 23.88 dB
A-31
A-32

N5625

Uploaded by

Document Information

Copyright

Available Formats

Share this document

Share or Embed Document

Sharing Options

Did you find this document useful?

Is this content inappropriate?

Copyright:

Available Formats

N5625

Uploaded by

Copyright:

Available Formats

Communication

Noise and distortion

Where are we in the Curriculum? . . . . . . . . . . .

Where are we (cont)? . . . . . . . . . . . . . . . . . .

Communication Lab Connection . . . . . . . . . . . .

Comm I/Comm II Course Sequence . . . . . . . . . . 1-10

Course Introduction and Overview . . . . . . . . . . . 1-11

1.10 A Block Diagram . . . . . . . . . . . . . . . . . . . . . 1-12

CHAPTER 1. COURSE INTRODUCTION/OVERVIEW

ECE 5625 Communication Systems I

Where are we in the ugrad and grad curriculum?

ECE 5625 Communication Systems I

Rapid Prototype, FPGA

CHAPTER 1. COURSE INTRODUCTION/OVERVIEW

Where are we in the Curriculum?

ECE 5625 Communication Systems I

1.3. WHERE ARE WE (CONT)?

Where are we (cont)?

Courses Offered According to Demand

ECE 5625 Communication Systems I

CHAPTER 1. COURSE INTRODUCTION/OVERVIEW

1GOTGU! "+>?(&+!V($*%K&! <%+B! "%)>R%&3! <%+B! 1GOTGU! .0WJ! "%)>R%&3! ;0WJ

ECE 5625 Communication Systems I

1.5. INSTRUCTOR POLICIES

Homework papers are due at the start of class

ECE 5625 Communication Systems I

CHAPTER 1. COURSE INTRODUCTION/OVERVIEW

Communication Lab Connection

ECE 5625 Communication Systems I

1.7. SOFTWARE TOOLS

ECE 5625 Communication Systems I

CHAPTER 1. COURSE INTRODUCTION/OVERVIEW

Comm I/Comm II Course Sequence

ECE 5625 Communication Systems I

1.9. COURSE INTRODUCTION AND OVERVIEW

Course Introduction and Overview

The theory of systems for the conveyance of information

Transcontinental telephone line completed

ECE 5625 Communication Systems I

CHAPTER 1. COURSE INTRODUCTION/OVERVIEW

A a high level communication systems are typically described

Noise and distortion

There is an information source as the input and an information

ECE 5625 Communication Systems I

1.11. CHANNEL TYPES

Electromagnetic-wave (EM-wave) propagation

When you think wireless communications this is the channel

CHAPTER 1. COURSE INTRODUCTION/OVERVIEW

ECE 5625 Communication Systems I

1.11. CHANNEL TYPES

Examples of public (commercial) and government (military

There is a hierarchy of organizations that regulate how the

CHAPTER 1. COURSE INTRODUCTION/OVERVIEW

At frequencies above 12 GHz oxygen and water vapor absorb

ECE 5625 Communication Systems I

1.11. CHANNEL TYPES

Guided EM-wave propagation

Communication using transmission lines such as twisted-pair

Magnetic recording channel

Disk drives, fixed (at one time flexible too)

ECE 5625 Communication Systems I

CHAPTER 1. COURSE INTRODUCTION/OVERVIEW

Example 1.1: Distortion in a Sat-Comm Channel

Wideband Sat-Comm simulation model