JOURNAL

OF

APPLIED

PHYSICS

VOLUME

36,

NUMBER

JANUARY

1965

A Stability Function for Explicit Evaluation of the Mullins-Sekerka

Interface Stability Criterion
R. F.

SEKERKA.

Westinghouse Research Laboratories, Pittsburgiz, Pennsylmnia

(Received 23 January 1964; in final form 3 August 1964)

.\ stability function S for explicit evaluation of the Mullins-Sekerka interface stability criterion is introduced and tabulated. Their criterion is then written in terms of S and compared with the constitutional
supercooling criterion for interface stability. From these results, experimental data can be analyzed and a
conclusive test of the stability theory can be made.

a previous paper by Mullins and Sekerka (called

I NM-S),1
it was shown that during the unidirectional
solidification of a dilute binary alloy at constant velocity, a planar solid-liquid interface is stable when
(1)

and unstable when the inequality is reversed. The notation here is the same as used bv 1\1 ullins and Sekerka;
it is summarized in Appendix i. We shall refer to (1)
as the M-S stability criterion; h is given by the expression
h= Imaxf(w) I,

We thus confine attention to the case for which A < 1.

Let us introduce a stability function S defined by the
equation
(4)

From the above considerations, it follows that

(5)

Then (1) becomes, for stability (note reversal of the inequality caused by multiplication by -1)

(2)

where

(6)

Introducing the dimensionless variables

y=(TMr/mGc)w2~O and tJ=.J-kU

(3)

Examination of Eqs. (2) and (3) shows that the determination of h by straightforward application of the
calculus involves the solution of a cubic equation in w.
But due to the cumbersome form of the analytic solution of a cubic equation, it is difficult to assess the M-S
criterion. It is the purpose of this paper to develop explicit expressions for h and to define and tabulate a related quantity S as a function of certain dimensionless
parameters. In this way, the predictions of the M-S
theory can be readily evaluated and compared with
other theories and with experiment; the use of dimensionless parameters alleviates the need to specify constants characteristic of a given material (often poorly
known) in order to give a complete theoretical analysis.

and defining a function (y) by the equation

A:(y) =

few)

2k

mC;,

(1 +tJy)!-l +2k'

---= y+-------

it follows that "c(y) has a minimum which obeys the

inequality
o~ [min(y)J~ 1
(8)
and that

s= l-[min(y)].

(9)

To find the value y= y", where "c(y) has its minimum

value we set

8(y)/

---

8y

INTRODUCTION OF A STABILITY FUNCTION S

=0
y~ljm

This condition yields

It was shown in M-S that for w~O

{}k

(1) f(w)~O,

(1+tJYm)l=~---_----.

[(1+tJYm)I-1 + 2kJ2

(2) O~ Imaxf(w) I ~mGc (note mGc~O),

(3) few) has one and only one maximum,

(4) for A ~ 1, where A is the dimensionless parameter,

k2

(7)

rv

TilT

rv

TM V

- - - - - - - - - - = k--- - - ,

(1-k) D (-mk"

Since (1+tJYm)L1+2k>O (for k>O) one can take the

square root of both sides of (10) without ambiguity of
sign. Introducing the substitution r= (1 +tJYm)t leads
readily to the following cubic equation for r:

D mGcD

r~+ (2k-l)r-

h = mG c and instability is impossible.

(10)

(2k/.ll) = O.

(11)

Writing (11) in the form

-----

W. W. Mullins and R. F. Sekerka, J. Appl. Phys. 35, 444

(1964).
1

264

r3= (2k/ A 1)+(1- 2k)r,

(12)

]\[ F L L I 1'\ S - S EKE R K A

I)J" T

E !{ F ACE S L<\ B r LIT Y C R I T E RIO N

one can plot the left and right sides of Eq. (12) as we
have done for three representative cases in Fig. 1. Xote
that the straight line (2k.'.1 i)+(1-2k)r always has a
positive intercept on the ordinate for positive A and k
while its slope may be positive or negative and depends
only on k. Hence, corresponding to k ~ 0, there exists
one and only one root r>O of Eq. (11); it is this positive
root which corresponds to positive w. Henceforth in this
paper, we shall refer to r as the real positive root of (11).
Obviously, from (11), r is a function of two dimensionless variables, A and 1<, and since
y",=(r L

(13)

ll(A/4k),

FIG.

1. Plot of

Efj. (11) as a function of r for (a) case

1-1 positin root, 2

conjugate imaginary
roots, (b) case II-l
positive root, 2 equal
negative roots, and
Ic) case III-l posi
tive root, 2 unequal
negative roots.

--

it follows from (9) that S is also a function of only "1

and k. Using (7), (9), (10), and (11) we readily find
.1

3Al

S(A,k)= 1+- - ---r 4k

2
EVALUATION OF

~+(1-2k)r
A'12

Roots

.4(1-2k)
---~r2.

(14)

4k
,~(A,k)

t1. Using (1-1-) and

Before treating the case of general A and k, we shall

present three approximate analytic expressions for
SeA ,k) corresponding to: (a) the limiting case A --> 0,
(b) the limiting case k --> 0, and (c) the special case
k=!. We consider these cases in turn.
Case (a). For verv small A (such that 2k/ A 11)
it is clear from Oi) that r1 and, in particular,
r3(2k-1)r. A useful approximation amounts to neglecting the linear term in (11) to get

(2k)1/3
(15)

r~--

A-+ll

265

A 1 If,

and using (14)

(1-2k)

,\)(.1,k) ~ 1-t(2k.1)!----(2kA)i+A ...O

4k
41,

(16)

or

SeA ,k) ~ I-H2kA)t,

(17)

4 ... 0

where (17) is the leading term of (16).

Case (b). In the mathematical limit 1?=O, we have
r=l; accordingly for kl we set r=l+~, where ~1
and proceed to do a simple perturbation calculation to
first order in small quantities. Thus (11) becomes
approxima tel y
(18)

S(A,k)

(19) then gives finally

~
k.... O

(1+A-2.1t)(I-k).

(20)

Case (c). For k=!, the linear term in (11) is zero so

r(A,!)=A-1I6. Then (14) readily yields

S(A,!)= 1-!A 1+..1/2.

(21)

Note that (17) agrees with the leading term of (21) for

1?=!, while (16) reduces exactly to (21) in that case.

For general A and k it is expedient to program the
calculations for computation by an IBM 7090 computer. Since only the positive root of (11) is required for
substitution into (14) and since (11) does not contain
a quadratic tern1, it is easier to make use of a straightforward application of the cubic formula than to use a
standard program for the three roots of a general cubic
and then select the positive root. Three cases arise,
depending on the relative sizes of A and k; the resulting
fornlUlas for r are given in Appendix II for reference .
The program was run for 16 values of k and for A
ranging from 10- 10 to 1. Using these results, Figs. 2 and
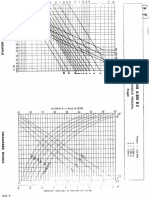
3 were constructed; in Fig. 2, S is plotted as a function
of A. for various k, while in Fig. 3 S is plotted against
log A. Together the plots cover the range of .1 where S
is substantially different from or 1.

THE M-S STABILITY CRITERION IN

TERMS OF S (A,k)

According to Eq. (6), stability obtains when

from which

(g'+g)/2mG c > SeA ,k).

~~k(~-l)+k~(~-~-!),
o AI
A! 2.1

(19)

Using the formulas 1

k ...

where we have selected the root of (18) which makes

(6)

K
c",(k-l) L
DkG c

--(g'-g)

(22)

266

R. F. SEKERKA
of material constants which are specified by a choice of
base material and solute and contains all other parameters except the above three variables of operation.
Within the approximation of dilute solutions, the material constant.s are independent of the kind and amount
of solute. "'ith the preceding classification of parameters, let us consider all of the material constants to be
fixed and suppress their explicit appearance in the
stability uiterion. Accordingly, we define a test function ,(G/V,c,,) by the equation

0.9
0.8
0.7

/Sfable
Unstoble

Proceeding t.o suppress the explicit appearance of the

material constants, we call
0.2

0.3

0.6

0.7

0.8

s( VI coo) = SeA ,k),

0.9

FIG. 2. Plot of the stability function S versus the dimensionless

stability parameter A for several values of the solute partition
coefficient k. A smooth interface is stable if the test function 'I'
fans above the appropriate curve.

and the definitions of ~J' and g, (22) can be written in

terms of experimentally measurable quantities as

k [L
GJ--->S(A,k).
D
--+--

2KL

~---

Ks+Kdl-k) 2KL

(25)

where we continue to use the symbol S without ambiguity because the left side of (25) is a function of
only one variable, the ratio (Vic",). Then for stability,
we need the test function to be greater than the stabilit:-" function, i.e.,
,(G/ V,c",) > s( V/ c",,).

(26)

For extremely small values of A where S -+ lone obtains

(23)

V (-mk"

'l(G/V,c",)

> 1,

(27)

A~()

It is interesting to divide the parameters of this

problem into two classes. The first class consists of the
three variables of operation, G, V, CoO' which can be
varied independently of the base material and kind (but
not amount) of solute, while the second class consists

0.9

O.B
0.7
0.6

0.5
0.4
Unstoble

0.3
0.2

dS
J1
> -2KL
- - [LV
--+G --G

0.1

910

which is the modified constitutional supercooling criterion of lVI-So It is very important to note that Eq. (26)
contains three independent variables of operation (constructed from the three fundamental variables, G, V, CoO,
while Eq. (27), as well as the constitutional supercooling
criterion of Tiller et al./ 3 depends on only two independent variables of operation. Indeed, to get the constitutional supercooling criterion for stability, one sets
KL=K,~ and L=O in (24) and uses (27). Thus, the inclusion of capillarity (S= 1 without capillarity) breaks
the ratio G/V, so to speak, and makes G, V, c'" individually important. It is for this reason that one can
have stability despite the presence of constitutional
supercooling, as pointed out by lVI-So
Let us cast Eq. (23) in still another form where it can
be easily compared with the constitutional supercooling
criterion. Using the notation 4 "gradient of constitutional supercooling," dS/dx=mGc-G, along with Eq.
(22) and reversing the sense of the inequality in (23)
we find that the :M-S theory predicts instability when

-9

-8

-7

-6

-5

-4

-3

Log,oA
FIG. 3. Plot of the ~tability function S versus logA for several
values of k. A smooth interface is stable if the test function 'I' falls
above the appropriate curve.

lix

K 8 +K L 2KL

(28)

2 W. A. Tiller, K. A. Jackson, J. W. Rutter, and B. Chalmers,

Acta Met. 1, 428 (1953).
3 J. W. Rutter and B. Chalmers, Can. J. Phys. 31, 15 (1953).
4 W. A. Tiller, J. App!. Phys. 33,3106 (1962).

1\1 U L LIN S- S EKE R K A

1 NT E R FA C EST A B I LIT Y

or

(29)

whereas the constitutional supercooling criterion predicts instability when

(30)

dS/dx>O.

Equations (29) and (30) show that for instability to

occur, not only must constitutional supercooling exist
but a definite gradient of constitutional supercooling must
exist. Indeed, as $ ----> 0, the amount of constitutional
supercooling needed for instability increases, finally
becoming infinite at $=0 which is the onset of the
absolute stability considered by 1\1-S.
CONCLUSIONS

We have explicitly evaluated the M-S stability criterion in terms of a stability function S and have compared the M-S theory with the theory of constitutional
supercooling. We have seen that the theories are somewhat similar for the case S~l but differ appreciably for
S substantially different from 1. We shall not attempt at
this time to make a detailed comparison with experiment. However, let us note that most experiments to
date have apparently been conducted in the range where
A1, and consequently [see Eq. (17)J S-1. The usual
procedure is then to plot G/V vs Coo and, according to
(24) and (27), get a straight line whose slope is related
to the diffusion coefficient D. Hence, since diffusion coefficients of liquid metals are often poorly known, it may
be useful to begin experiments in the region of low velocities and high solute content so that A --j- 0 and from
the slope of a straight line plot of G/V and c"" determine
D. Then one can proceed to higher velocities and lower
concentrations and use the determined value of D to
evaluate A.
ACKNOWLEDGMENTS

This work was partially supported by the U. S. Air

Force Office of Scientific Research under Contract
AF 49(638)-1029. The author would like to thank Dr.
W. W. Mullins, Department of Metallurgical Engineering, Carnegie Institute of Technology, and Dr. W. A.
Tiller, Crystallogenics Section, Westinghouse Research
Laboratories, for their many helpful suggestions and
for their help in preparing the manuscript.

eRr T E RIO N

267

TjJ = melting point of the pure solvent (OK)

L=latenl heat of fusion per unit volume of the pure
sol ven t (erg/ cm 3)
K L= thermal conductivity of the liquid (erg/cmsec-deg)
K 8= thermal conductivity of the solid (ergs/ cm-sec-deg)
K=(K L +K s )/2=average thermal conductivity of
the system (ergs/cm-sec-deg)
g=G(KL/K)=generalized gradient in the liquid
(deg/cml
g'=Gs(KsiK)=generalized gradient in the solid
(degcm)
Coo = concentration of solute in the liquid far from the
interface (wt.%)
1<= partition coefficient of solute in solven t (dimensionless)
m= slope of liquidus line on phase diagram (deg/wt.%)
D= diffusion coefficient in the liquid (cm2/sec)
Gc =average 5 solute gradient in the liquicl (wt.%/cm)
'Y=solid-liquid surface free energy/unit area (erg/
cm2)
1'= '}'/L = capillarity constant (cm)
w= 27r per wavelength of sinusoidal perturbation of
interface (em-I)

k 2 rv TM
rv 1'11'1 V
A=--------=k--(1-k) D (-m)c",
D mGeD

= stability parameter (dimensionless),

APPENDIX II

A straightforward application of the cuhic formula 6

leads to the following expression for r, the positive root
of (11):
(Al)
r=a+l1,
where a and f3 are given below for the three cases which
occur. Define

k2

(2k-l)3

27

F=-+---.

(A2)

Then Case (1)

If F?;O and (F)!~k/A~,

a= [ kl + (F)!]t
."4 '

(A3a)

APPENDIX I

(A3b)

v = average" velocity of freezing

(em/sec)
temperature gradient III the liquid

G=average 5
(deg/cml
Gs =average 5 temperature
(deg/cm)

gradient

In

the

solid

" Means an li\erage O\er a cross section of the sample at the

interface.
6Handbook 0/ Chemistry and Physics (Chemical Rubber
Company, Cleyeland, Ohio, 1961), 43rd ed., p. 318.