.

Maxima and Minima

.
Definition. Let R be any region on the xy-plane, a function f (x, y) attains its
absolute or global, maximum value M on R at the point (a, b) of R if
(i) f (x, y) M for all points (x, y) in R, and
. M = f (a, b).
(ii)

Similarly, we can define the global minimum as well.

.
Function f (x, y) attains the absolute or global, minimum value m on R of at the
point (a, b) of R if
(i) f (x, y) m for all points (x, y) in R, and
.(ii) m = f (a, b).

. . . . . .

Matb 210/Math200 in 2014-2015

.
Example. Prove that the function f (x, y) = x + y attains a maximum value 2
and
. minimum value 0 on the square R = { (x, y) | 0 x 1, and 0 y 1 }.

Proof. For any point P(x, y) in R, one has 0 x 1 and 0 y 1, so it follows

that
0 = 0 + 0 x + y 1 + 1 = 2.
So 0 f (x, y) 2, which satisfies the condition (i). Moreover
f (0, 0) = 0 + 0 = 0, and f (1, 1) = 1 + 1 = 2 such that (0, 0) and (1, 1) are in R,
in which the condition (ii) holds.

. . . . . .

Matb 210/Math200 in 2014-2015

. Local Extreme Values
.
Definition. Let f (x) be a function defined in a domain D of Rn (n = 2, 3), and a
point x0 D. Function f is said to attain its local maximum at x0 , if there exists
. > 0 such that f (x0 ) f (x) for all x B(x0 , ) D.
Remarks. (i) In general, a function can have many local maxima, and can have
no local maxima in its domain.
(ii) The concept of local minimum is similarly defined.
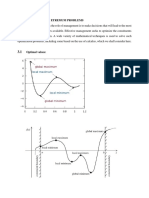
xz-cross section z = fm (x, y) = (x2 + y2 )2 + mx

xz-cross section
z = fm (x, y) = (x2 + y2 )2 + mx

. . . . . .

Matb 210/Math200 in 2014-2015

. Existence Theorem of Global Extremum
.
Theorem. A continuous function always attains its global maximum and global
minimum
. values, if its domain is closed and bounded.

Remarks. (a) One can replace the condition on the domain by a simple but
more restrictive one, such as, the domain consists of the points on and within a
simple closed curve.
(b) The proof of this theorem requires Heine-Borel cover theorem.
.
Definition. A simple closed curve is a parameterized continuous curve r(t) for
t [a, b], such that (i) r(a) = r(b), and the vectors r(t) are different from each
.other except when t = a and t = b.
.
Let D be consist of points on and within a simple and closed curve. One can
prove that (i) the points in D that are not on the curve are interior points; and
.(ii) those that are on the curve called boundary points.

. . . . . .

Matb 210/Math200 in 2014-2015

.
Example Let f (x, y) = x2 + y2 on the region R = { (x, y) | x2 + y2 1 }.
Determine
. the absolute minimum of f on R.

Solution. As R is closed and bounded region in R2 , so f attains its absolute

minimum. As the square root is non-negative, so f (x, y) 0 = f (0, 0) for all
(x, y) in R.The minimum of the function f on R is given by f (0, 0) = 0. However,
f (x, 0) = x2 + 02 = |x|, which is not differentiable at x = 0, and hence fx
does not exist at (0, 0).
Remark. It is an example that the absolute minimum occurs at which f (x, y)

does not have partial derivatives.

. . . . . .

Matb 210/Math200 in 2014-2015

.
Necessary Conditions for Local Extremum
.
Theorem. Suppose that f (x, y) is a continuous on region D in plane. If
(i) f (x, y) attains a local maximum value at an interior point (a, b) in D, and
(ii) both the partial derivatives fx (a, b) and fy (a, b) exist,
Then
. fx (a, b) = fy (a, b) = 0.

The theorem gives only a necessary condition for existence of a local extreme
point provided that all the first order partial derivatives exist. It can happen that
at a local extreme point, some of the first partial derivatives do not exist.
.
Definition. A point P in the domain of f is called a critical point of f , if (i) all first
order partial derivatives of f at P exist and are equal to 0, or (ii) at least a first
.order partial derivatives of f does not exist.

. . . . . .

Matb 210/Math200 in 2014-2015

.
Types of Absolute Extremum
.
Theorem. Suppose that f is continuous on the plane region R consisting of the
points on and within a simple closed curve C. If f (a, b) is either the absolute
maximum or the absolute minimum value of f (x, y) on R, then (a, b) is either
1. An interior point of R at which f (a, b) = f (a, b) = 0,
x y
2. An interior point of R where not both partial derivatives exist, or
3. A point of the boundary curve C of R.
.
.
Definition. A point which satisfies the above conditions (1) or (2) is called a
.critical point of the function f .
.
Proposition. Any extreme value of the continuous function f on the plane
region R, bounded by a simple closed curve, must occur at an interior critical
point
. or at a boundary point.

. . . . . .

Matb 210/Math200 in 2014-2015

.
Notation. For any given f , one write f (x, y) = fx (x, y)i + fy (x, y)j = (fx , fy ) at
.point (x, y).
.
If f has 1st order partial derivatives on its domain, then
(a, b) is a critical point of f f (a, b) = (0, 0).
So one can think of this condition as a set of equations to determine the
possible
. interior critical points.

. . . . . .

Matb 210/Math200 in 2014-2015

.
Notation. For any given f , one write f (x, y) = fx (x, y)i + fy (x, y)j = (fx , fy ) at
.point (x, y).
.
If f has 1st order partial derivatives on its domain, then
(a, b) is a critical point of f f (a, b) = (0, 0).
So one can think of this condition as a set of equations to determine the
possible
. interior critical points.
.
Example. Define f (x, y) = x2 + y2 on R2 . It is easy to see that the partial
derivatives fx and fy exist only for all (x, y) = (0, 0). Moreover,

f (h,0)f (0,0) h2 |h|
h = h = h which is equal to 1 if h > 0, and equal to 1 if h < 0.
f (h,0)f (0,0)
So the limit lim h does not exist, i.e. fx (0, 0) does not exist.
h0
However, the function f attains the global minimum value at (x, y) = (0, 0), so
.the theorem fails to apply to apply as the condition is not satisfied.

. . . . . .

Matb 210/Math200 in 2014-2015

.
Example. Find the maximum and minimum values by the function
f (x, y) = xy x y + 3 at the points of the triangular region R in the xy-plane
with
. vertices at O(0, 0), A(2, 0) and B(0, 4).

Solution. (Existence) As R is a closed and bounded set in R2 , so one knows

that the continuous function f must attains extremum values at some points in
R together with the boundary of AOB.
(Interior Critical Points) As f is a polynomial, so both fx and fy exist at any
interior points of R. According to the theorem above, to search for the interior
extremum point of f , one needs to determine the interior critical points of f in
AOB. Then f (x, y) = (fx (x, y), fy (x, y)) = (y 1, x 1), so (x, y) = (1, 1) is
the only critical point of f .
So one needs to consider the boundary points of R as well.

. . . . . .

Matb 210/Math200 in 2014-2015

.
Example. Find the maximum and minimum values by the function
f (x, y) = xy x y + 3 at the points of the triangular region R in the xy-plane
with
. vertices at O(0, 0), A(2, 0) and B(0, 4).

Solution. (Boundary Points) Consider the bound-

ary points of R, i.e. points on the boundary of
AOB.
AO : g(x) = f (x, 0) = x + 3 for 0 x 2.
max g = 3, min g = 1.
BO : h(y) = f (0, y) = y + 3 for 0 y 4.
max h = 3, min h = 1.
AB : Parameterize segment AB by


r(t) = OA + tAB = (2, 0) + t(2, 4) = (2 2t, 4t) for 0 t 1.
AB : k(t) = f (2 2t, 4t) = (2 2t)(4t) (2 2t) 4t + 3 = 8t2 + 6t + 1 for
0 t 1. k (t) = 16t + 6, so t = 6/16 = 3/8 is a critical point for k.
max k = max{k(0), k(1), k(3/8)} = max{1, 1, 17/8} = 17/8, and
min k = min{k(0), k(1), k(3/8)} = 1. Finally, on the region R we have
max f = max{17/8, f (1, 1) = 2, 3} = 3, and min f = 1. . . . . . .

Matb 210/Math200 in 2014-2015

.
Example. Find the maximum and minimum values of the function
f (x, y) = xy x y + 3 for the point on the unit disc
. = { (x, y) | x + y 1 }.
D 2 2

Solution. As f is a polynomial, it follows from the law of limits that its first order
partial derivatives exist on R2 . For interior critical point, we have
f (x, y) = (0, 0) if and only if (0, 0) = (fx (x, y), fy (x, y)) = (y 1, x 1), i.e.
(x, y) = (1, 1). In this case, the point (1, 1) does not lie in the disc D. So both
maximum and minimum values occur at the boundary points of D, which is the
unit circle C. Then we parameterize C : r(t) = (cos t, sin t) for 0 t 2.
Define the function g(t) = f r(t) = f (cos t, sin t) = sin t cos t sin t cos t + 3,
which is a differentiable function of one variable on the closed interval [0, 2 ].
One can use derivative test of one variable to find the maximum and minimum
value of g, and hence that of f .
Remark. Here we skip the details for the sake of time. We will work out this
problem again in Lagrange multiplier.

. . . . . .

Matb 210/Math200 in 2014-2015

. Differentiable Functions
Let f be a function of single variable y = f (x), an increment x of input x
means x 7 x + x, then there is an increment in output y defined as
y = f (x + x) f (x).
Since derivative of f at x, exists, we adjust further by linear approximation term
f (x)x, then we have
y = f (x + x) f (x) = f (x)x + (x) x,
f (x + x) f (x) f (x)x
where (x) = denotes a small quantity, in which
x
one expects that limit procedure will kill this term as x 0, that is
lim (x) = 0.
x0

. . . . . .

Matb 210/Math200 in 2014-2015

In view of the definition of y = f (x + x) f (x) = f (x)x + (x) x, and
f (x + x) f (x) f (x)x
the condition lim (x) = lim = 0, we introduce
x0 x0 x
the concept of differential dx, dy as mathematical object to represent the
relationship of this increment relation,
dy = f (x)dx,
in which dx and dy can be interpreted as linear increments geometrically.

. . . . . .

Matb 210/Math200 in 2014-2015

Let z = f (x, y) be a function defined on domain D, and P(a, b) is a point in D.
Define the increment f = f (a + x, b + y) f (a, b) at P(a, b), which depends
only on (x, y). Like the one variable case, we subtract the linear part from
increment, and then divide by x2 + y2 to obtain
f (a + x, b + y) f (a, b)fx (a, b)x fy (a, b)y
(x, y) = , which is a new
x2 + y2
function depending on (x, y) only.
.
Definition. Let z = f (x, y) be a function defined on domain D, and P(a, b) is a
point in D. f is called differentiable at a point P(a, b), if
lim (x, y) = 0.
.(x,y)(0,0)
.
Definition. f is differentiable on its domain D, if f is differentiable at every point
. D.
in
.
Proposition. If f is a differentiable function, then all 1st order partial derivatives
. f exist. However, the converse does not hold.
of
. . . . . .

Matb 210/Math200 in 2014-2015

. Differentiable Functions of n varibles
.
Definition. The definition of differentiability of a function at a point can be
generalized to for function of more than 2 variables. Moreover, we assume that
f has 1st order partial derivatives in D.
Suppose that f = f (x) is a function of n variables x = (x1 , , xn ), defined on
the domain D Rn . Let a = (a1 , , an ) be a fixed point in D instead of
(a, b) R2 , and h = (h1 , , hn ) instead (x, y).
Define the following scalar function which only depends only h as follows
f (a + h) f (a) f (a) h
(h) = . Then we f called differentiable at a, if
h
lim (h) = 0.
.h0
.
Remark. In general, it is very difficult to verify that a given function of
multi-variables
. is differentiable.

. . . . . .

Matb 210/Math200 in 2014-2015

. Differential of a scalar function of n variables
.
Definition. Let f = f (x1 , , xn ) be a differentiable function (or least 1st oder
the partial derivatives of f exist) on D Rn , then the differential of f , denoted
by df , which can be reduced to the differentials of the coordinate functions
defined on D as well:
n
df (a) = f (a) dx = fxi (a)dxi .
. i=1

.
Remark. Though we can not give a very concise definition of differential of a
scalar function f in this course, but one should compare it with the linear
approximation of f in the later section. In this case, the local variation of f can
.be described linearly in terms of variation dxi of position changes.

. . . . . .

Matb 210/Math200 in 2014-2015

.
Proposition. (i) If f is a polynomial function, then f is differentiable;
(ii) If f and g are differentiable functions defined on D, such that then the
following functions s(x) = f (x) + g(x), d(x) = f (x) g(x) , p(x) = f (x) g(x)
f (x)
and q(x) = g(x) are differentiable on D, provided g(x) = 0 for all x in D.
(iii) In particular, a rational function is a differentiable at every point in the
.domain D.
.
Proposition. Let f be a scalar differentiable function defined in a domain D of
Rn with range R, and g is a scalar differentiable function defined on the set R,
f g
i.e. D R R. Then the composite function g f is a scalar differentiable
.function defined on D.
.
Remark. In fact, all the elementary functions are differentiable on their domain,
which it follows from the two propositions above that we have a large class of
differentiable
. functions.

. . . . . .

Matb 210/Math200 in 2014-2015

.
x2 y2
Example. Let f (x, y) = x2 +y2
for all (x, y) = (0, 0), and f (0, 0) = 0. Prove that f
.is differentiable on R2 .
Solution. From the proposition above, one knows that f is differentiable on
R2 \ {(0, 0)}. It remains to show that f is differentiable at P(0, 0). For this, one
has to check that the first partial derivative exist. Indeed
fx (0, 0) = lim
f (0+h,0)f (0,0)
h = lim 0h 0 = 0, and similarly fy (0, 0) = 0. Now we
h0 h0  
 f (0+x,0+y)f (0,0)fx (0,0)xfy (0,0)y 
need to check that |((x, y)| =   
(x)2 +(y)2 
 
 (x)2 (y)2 
 ( (x)2 +(y)2 )3/2 = (x)2 + (y)2 .
2 2 2
=  (x)2 +(y)2 1
(x)2 +(y)2  4( (x) +(y) )
( )2
In fact, the inequality is due to AM-GM inequality ab a+2 b .
Then it follows from the sandwich theorem of limit that
lim (x, y) = 0.
(x,y)(0,0)

. . . . . .

Matb 210/Math200 in 2014-2015

.
Definition. For any differentiable f and a point P(a, b) in its domain, let

L(x, y) = f (a, b) + fx (a, b)(x a) + fy (a, b)(y b)

= f (a, b) + f (a, b) (x a, y b)

.be the linear approximation of f at the point P(a, b).

Remark. For any fixed P(a, b), the function L(x, y) associated to a function f at
P(a, b) has a graph z = L(x, y) which is the tangent plane.
.
Example. Approximate the number (3.2 2 2
) + (3.9) using the linear
2 2
.approximation to the function f (x, y) = x + y at (3, 4).
Solution. f (x, y) = ( y
x
, ), and f (3, 4) = (3/5, 4/5), so the
x2 +y2 x2 +y2
linear approximation of f (x, y) at (3, 4) is given by
L(x, y) = f (3, 4) + f (3, 4) (x 3, y 4)
= 5 + 53 (x 3) + 45 (y 4). Then the number (3.2)2 + (3.9)2 can be
approximated by L(3.2, 3.9) = 5 + 53 0.2 45 0.1 = 5 + 25
3
25
2
= 5.04.

. . . . . .

Matb 210/Math200 in 2014-2015

.
Definition. In general, if f is a function defined in a domain D in Rn (n = 2, 3),
and P(x0 ) is a point in D, then the linear approximation of f at P is given by

L(x) = f (x0 ) + f (x0 ) (x x0 ),

f f f
= f (x0 ) + x1 (x0 ) (x1 a1 ) + x2 (x0 ) (x2 a2 ) + + xn (x0 ) (xn an ),
f f f
where f (x0 ) = ( x (x0 ), x (x0 ), , xn (x0 ) ), x0 = (a1 , , an ), and
1 2
x. = (x1 , , xn ).
.
Example. The function f (x, y) = 6x2 2x3 + y3 + 3y2 has n critical points, then
.n = .

Solution. f (x, y) = (12x 6x2 , 3y2 + 6y), f (x, y) = (0, 0) if and only
0 = 6x(x + 2) and 0 = 2y(y + 2), it follows that
(x, y) = (0, 0), (2, 0), (0, 2), (2, 2) are the critical points of f . Then n = 4.

. . . . . .

Matb 210/Math200 in 2014-2015

.
Chain Rule I
.
If w = f (x, y) has continuous first-order partial derivatives and that
r(t) = (x(t), y(t)) is a differentiable curve in the domain of f , then
(i) the composite function F(t) = w r(t) = f (x(t), y(t)) is a differentiable
function of t, and (ii) its derivative is given by
dF w dx w dy
= + = f (r(t)) r (t).
.dt x dt y dt
z

T P(x, y, z)

3 x

Remark. In the figure, we draw a straight line instead a curve in the xy-plane.
. . . . . .

Matb 210/Math200 in 2014-2015

.
dz
Example. Use the chain rule to find at t = 1 if
dt
dx
z = arctan(yx2 ), x = x(t), y(t) = t2 , and (1) = x(1) = 1.
. dt
z 1 2xy z x2
Solution. First = (yx2 ) = , and =
x 1 + (yx ) x
2 2 2
1 + (yx ) 2 y 1 + (yx2 )2
dz z dx y dy 2xy dx x2
= + = + 2t. When t = 1, we
dt x dt y dt 2 2
1 + (yx ) dt 1 + (yx2 )2
have x(1) = x (1) = 1, y(1) = 1, and y (1) = 2. Then
dz  2 1
 = 1 + 2 = 1 + 1 = 2.
dt t=1 2 2

Remark. Read the examples in your text!

. . . . . .

Matb 210/Math200 in 2014-2015

.
Chain Rule II
.
Theorem. Suppose that w = f (x, y, z) is a differentiable function, where
x = x(u, v), y = y(u, v), z = z(u, v), where the coordinate functions are
parameterized by differentiable functions. Then the composite function
w(u, v) = f ( x(u, v), y(u, v), z(u, v) ) is a differentiable function in u and v,
such that the partial functions are given by
w w x w y w z
= + + ;
u x u y u z u
w w x w y w z
= + + .
. v x v y v z v
.
Example. Let f (x, y, z) = x3 + y2 + z, and x = x(u, v) = uv, y = y(u, v) = u + v,
z = z(u, v) = u/v. Evaluate the partial derivatives of
. (u, v) = f (x(u, v), y(u, v), z(u, v)) with respect to u and v by two methods.
S

Solution. (i) S(u, v) = f (uv, u + v, u/v) = u3 v3 + (u + v)2 + u/v, then

S S
u = 3u v + 2(u + v) + v , and v = 3u v + 2(u + v) v2 .
2 3 1 3 2 u

S S x S y S z
(ii) u = x u + y u + z u
= 3x2 v + 2y 1 + 1 v1 = 3(uv)2 v + 2(u + v) 1 + 1 1v .
. . . . . .

Matb 210/Math200 in 2014-2015

.
Example. Suppose that w = f (x, y) has continuous first-order partial
derivatives and that the coordinates (x, y) are functions of the other variables
r, such as in polar coordinates, i.e x(r, ) = r cos , and y(r, ) = r sin .

By means of the new coordinates, w becomes a function in the variables r, ,

Namely, by means of composition, we have w(r, ) = w(x(r, ), y(r, )), for
example f (r cos , r sin ) in terms of polar coordinates.

The partial derivative w

r can be evaluated by treating the variable as a fixed
constant, so it follows from the chain rule stated above that
w w x w y
= + .
. r x r y r

. . . . . .

Matb 210/Math200 in 2014-2015