Professional Documents
Culture Documents
F (T) 1 F (T)
Uploaded by
洪子翔0 ratings0% found this document useful (0 votes)
28 views7 pagesThe document presents 4 problems related to economics and optimization. Problem 1 covers constant hazard rates, life annuities, and expected costs. Problem 2 examines a war of attrition game. Problem 3 analyzes an n-firm oligopoly with market dynamics. Problem 4 considers a monopoly engaging in cost reduction R&D to maximize present value profit over time.
Original Description:
s17ex1 (1)s17ex1 (1)
Original Title
s17ex1 (1)
Copyright
© © All Rights Reserved
Available Formats
PDF, TXT or read online from Scribd
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentThe document presents 4 problems related to economics and optimization. Problem 1 covers constant hazard rates, life annuities, and expected costs. Problem 2 examines a war of attrition game. Problem 3 analyzes an n-firm oligopoly with market dynamics. Problem 4 considers a monopoly engaging in cost reduction R&D to maximize present value profit over time.
Copyright:
© All Rights Reserved
Available Formats
Download as PDF, TXT or read online from Scribd
0 ratings0% found this document useful (0 votes)
28 views7 pagesF (T) 1 F (T)
Uploaded by
洪子翔The document presents 4 problems related to economics and optimization. Problem 1 covers constant hazard rates, life annuities, and expected costs. Problem 2 examines a war of attrition game. Problem 3 analyzes an n-firm oligopoly with market dynamics. Problem 4 considers a monopoly engaging in cost reduction R&D to maximize present value profit over time.
Copyright:
© All Rights Reserved
Available Formats
Download as PDF, TXT or read online from Scribd
You are on page 1of 7
Midterm (take-home exam) May 10, 2017
1. Let F (t) be the distribution function of the length
of an individuals life in a group of population. The
F (t)
hazard rate () at time t is h(t) 1F (t) .
(a) Find the distribution function for the
constant hazard rate case h(t) = . (Hint: F (t)
satisfies a LCCDE. It is also a separable variable
DE. The initial condition is F (0) = 0.)
Consider a life annuity () that pays $ 1 per
unit of time to the recipient beginning at age t0 .
The present value (PV) at t0 of the payment if the
Rt r (tt )
recipeint lives to age t is t0 e r ( t0 ) d = 1e r 0 .
(b) Calculate the expected cost to provide such
R r (tt ) F (t)
an annuity t0 1e r 0 1F (t0 ) dt. (In this case
the conditional distrbution of the remaining life is
independent of the age.)
(c) Find the distribution function for the case
h(t) = (1 t)1, 0 t 1. (Hint: F (t) is a
LDE as well as a separable variable DE.)
(d) Let = 2. Calculate the expected cost at t0
to provide the life annuity described above. if the
life annuity begins at age t0 :
R 1 1e r (tt0 ) F (t)
t0 r 1F (t0 ) dt.
2. In the war of attrition game, let the hazard rate of
F () 1
the distribution be 1F () = (1 ) , 0 1.
(a) Solve FOC to find the symmetric equilibrium.
(b) Is the 2nd order condition for player 1s
optimization problem satisfied?
3. Consider the dynamic n-firm oligopoly game:
market dynamics: p = a q1 . . . qn p
cost function: Ci (qi ) = 12 qi2
R
Profit function: i = 0 e rt [pqi C (qi )]
State variable: p Control variables: q1, ..., qn
(a) Find the DE of (p, m) for the symmetric
open-loop equilirium.
(b) Solve the problem to find the path of p(t)
and q(t).
(c) Calculate the HJB equation of Vi (p) and the
FOC for a feedback equilibrium.
(d) Guess V = A bp + c2 p 2 in a symmetrical
equilibrium. Find b and c.
(e) Find the closed-loop strategy qi as a function
of p.
(f) Derive the DE for the equilibrium path of
p(t) and find the limit pf = limt p(t).
(h) Calculate limn pf and explain.
4. (HW 19.2) (Monopoly and cost reduction R&D)
Consider an infinitely lived monopoly. The profit at
moment t is given by [1 c(t)]2 where c(t) is unit
production cost at t. (e.g., it has a static demand
function given by q(t) = 4(1 p(t)).) The
monopoly is engaged in cost reduction R&D. At
each moment t, the expenditure on R&D is given
by 0.5c(t)2 . Let the discount rate be r . Given the
time path of the unit production cost c(t) 0,
0 t < , the present value of the monopoly
profit stream
Z is n o
rt 2 2
e [1 c(t)] 0.5c(t) dt.
0
Given c(0), an optimal solution is characterized by a
time T such that c(t) > 0 for t < T and c(t) = 0
for t T . The problem of the monopoly becomes
to find a T to maximize a fixed time calculus of
variation problem:
Z T n o
rt 2 2
max e [1 c(t)] 0.5c(t) dt+e rT /r .
T ,c(t) 0
A transversality condition states that at T ,
c(T ) = 0. (Of course, by definition, c(T ) = 0.)
(a) Let r = 3. Derive the Euler equation for the
calculus of variation problem.
(b) Let c(0) = 0.25. Make use of the results of
problem 17.4 to solve the Euler equation to
obtain the cost path c(t), 0 t T .
(c) What can you say if c(0) = 1?
(d) Let r = 2. Given c(0) = 1, solve the
problem.
(e) Explain the difference between the results of
(b), (c), and (d).
You might also like
- Ece45 HW2Document5 pagesEce45 HW2PedNo ratings yet
- From Binomial Trees To The Black-Scholes Option Pricing FormulasDocument6 pagesFrom Binomial Trees To The Black-Scholes Option Pricing FormulasowltbigNo ratings yet
- Problem Weight Score 15 18 16 15 17 20 18 16 19 16 20 15 Total 100Document6 pagesProblem Weight Score 15 18 16 15 17 20 18 16 19 16 20 15 Total 100bbb bbbxNo ratings yet
- Ma Kai-Kuang (Tutorial+Lectures)Document157 pagesMa Kai-Kuang (Tutorial+Lectures)Ang KhengNo ratings yet
- sns 2022 중간Document2 pagessns 2022 중간juyeons0204No ratings yet
- HW 5Document2 pagesHW 5Kuann CNo ratings yet
- 4.1 Introduction To Angle ModulationDocument39 pages4.1 Introduction To Angle Modulation120200421003nNo ratings yet
- The Zero-State Response Sums of InputsDocument4 pagesThe Zero-State Response Sums of Inputsbaruaeee100% (1)
- Assignment 4 SolutionsDocument5 pagesAssignment 4 SolutionsHIGH DARBHANGANo ratings yet
- 2A1G Partial Differential EquationsDocument6 pages2A1G Partial Differential EquationsJohn HowardNo ratings yet
- CT A1Document3 pagesCT A1TtNo ratings yet
- Interest Rate Models 19.1 Basic Elements in A Bond Market: T T T U TDocument4 pagesInterest Rate Models 19.1 Basic Elements in A Bond Market: T T T U TowltbigNo ratings yet
- Solution of Ordinary Differential Equations: 1 General TheoryDocument3 pagesSolution of Ordinary Differential Equations: 1 General TheoryvlukovychNo ratings yet
- Lab Script Exp 3 (Fourier Synthesis)Document12 pagesLab Script Exp 3 (Fourier Synthesis)mouazam KhalidNo ratings yet
- B Splines PDFDocument7 pagesB Splines PDFhello worldNo ratings yet
- Topic 04: Complex Integration: MA201 Mathematics IIIDocument41 pagesTopic 04: Complex Integration: MA201 Mathematics IIIhaNo ratings yet
- Signals and Systems - CMP 271 Homework 7: Must NOTDocument2 pagesSignals and Systems - CMP 271 Homework 7: Must NOTsaad aliNo ratings yet
- Section 13.2 Derivatives and Integrals of Vector FunctionsDocument3 pagesSection 13.2 Derivatives and Integrals of Vector FunctionsAlvin AdityaNo ratings yet
- DSP4 Fourier Series - UnlockedDocument46 pagesDSP4 Fourier Series - UnlockedluisperikoNo ratings yet
- Fourier Series and Fourier Transforms: EECS2 (6.082), MIT Fall 2006 Lectures 2 and 3Document18 pagesFourier Series and Fourier Transforms: EECS2 (6.082), MIT Fall 2006 Lectures 2 and 3Uzmah JavedNo ratings yet
- ELEC221 HW04 Winter2023-1Document16 pagesELEC221 HW04 Winter2023-1Isha ShuklaNo ratings yet
- Ecuaciones Tarea 2Document5 pagesEcuaciones Tarea 2Luis SantibañezNo ratings yet
- MCQ 18ce310 Fourier Series and Partial Differential EquationsDocument8 pagesMCQ 18ce310 Fourier Series and Partial Differential EquationsGnanarajNo ratings yet
- Oil and Gas PricesDocument15 pagesOil and Gas Prices3revosNo ratings yet
- 10 Function Spaces: 10.1 Ordinary Linear Differential EquationsDocument15 pages10 Function Spaces: 10.1 Ordinary Linear Differential EquationsBruno PretoNo ratings yet
- CA2019 Topic 04 PDFDocument72 pagesCA2019 Topic 04 PDFDeepanshu RewariaNo ratings yet
- Space Curves 1Document12 pagesSpace Curves 1John KimaniNo ratings yet
- Pde1 PDFDocument11 pagesPde1 PDFkeith mushiningaNo ratings yet
- Modern Approaches To Stochastic Volatility CalibrationDocument43 pagesModern Approaches To Stochastic Volatility Calibrationhsch345No ratings yet
- 2017optimalcontrol Solution AprilDocument4 pages2017optimalcontrol Solution Aprilenrico.michelatoNo ratings yet
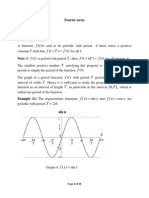
- Fourier SeriesDocument29 pagesFourier SeriesAngelo Toledo TamboongNo ratings yet
- Spring Term Instructor: Ahmet Ademoglu, PHDDocument2 pagesSpring Term Instructor: Ahmet Ademoglu, PHDferdi tayfunNo ratings yet
- Optimal Gradual Liquidation of Equity From A Risky Asset: Nikolai DokuchaevDocument8 pagesOptimal Gradual Liquidation of Equity From A Risky Asset: Nikolai DokuchaevndokuchNo ratings yet
- Module-2: Tensor Calculus: Lecture-16: The Time Derivative and Some Integral TheoremsDocument7 pagesModule-2: Tensor Calculus: Lecture-16: The Time Derivative and Some Integral TheoremsHamza SiddiquiNo ratings yet
- Metodo de HeunDocument6 pagesMetodo de HeunNilton Isaias Mariños HerreraNo ratings yet
- Fourier Series NOTESDocument67 pagesFourier Series NOTESAzue RamliNo ratings yet
- Math Transform Methods: Dr. P Adraig KirwanDocument57 pagesMath Transform Methods: Dr. P Adraig KirwanXavimVXSNo ratings yet
- Fourier Series Notes Corrected PDFDocument39 pagesFourier Series Notes Corrected PDFProma ChakrabortyNo ratings yet
- Fourier Series Notes (New)Document46 pagesFourier Series Notes (New)Shashank SinghNo ratings yet
- Exponential Distribution: Most Widely Used Probability Distribution in Reliability AssessmentDocument5 pagesExponential Distribution: Most Widely Used Probability Distribution in Reliability AssessmentKrishna Kumar AlagarNo ratings yet
- ME311 Autumn2021 T4Document2 pagesME311 Autumn2021 T4Varun PathakNo ratings yet
- Assignment 1Document16 pagesAssignment 1secidih495No ratings yet
- Problem Set 3: More On The Ramsey Model: Problem 1 - Social Planner ProblemDocument11 pagesProblem Set 3: More On The Ramsey Model: Problem 1 - Social Planner ProblemDaniel GNo ratings yet
- Differential OperatorsDocument4 pagesDifferential OperatorsErick SuparmanNo ratings yet
- HW - 2 Solutions (Draft)Document6 pagesHW - 2 Solutions (Draft)Hamid RasulNo ratings yet
- Problem Set 02: Harif University of TechnologyDocument4 pagesProblem Set 02: Harif University of TechnologyParsa AseminiaNo ratings yet
- EEE 303 HW # 1 SolutionsDocument22 pagesEEE 303 HW # 1 SolutionsDhirendra Kumar SinghNo ratings yet
- Equivalenceof StateModelsDocument7 pagesEquivalenceof StateModelsSn ProfNo ratings yet
- Fourier FullDocument41 pagesFourier FullIraqi for infoNo ratings yet
- Fourier Series NotesDocument39 pagesFourier Series NotestanmayeeNo ratings yet
- Principles of Communication Systems Homework 1Document3 pagesPrinciples of Communication Systems Homework 1NITYA SATHISHNo ratings yet
- Introduction To Frequency Domain ProcessingDocument55 pagesIntroduction To Frequency Domain Processingसुमित नेमाNo ratings yet
- Linear Time-Invariant SystemsDocument30 pagesLinear Time-Invariant SystemsJoseph IbrahimNo ratings yet
- 5 Ordinary Differential Equations: 5.1 GeneralitiesDocument16 pages5 Ordinary Differential Equations: 5.1 GeneralitiesYanira EspinozaNo ratings yet
- MA322 Past PaperDocument5 pagesMA322 Past PaperWenxiaoNo ratings yet
- 6 Fourier SeriesDocument43 pages6 Fourier SeriesutpNo ratings yet
- Midterm Solutions 2013Document12 pagesMidterm Solutions 2013Nonitus OctingentiNo ratings yet
- Chapter 4Document20 pagesChapter 4EricBSNo ratings yet
- hw2 SolDocument7 pageshw2 Solpriyankakaswan19No ratings yet
- Computational Engineering: Tackling Turbulence With (Super) ComputersDocument30 pagesComputational Engineering: Tackling Turbulence With (Super) ComputersCarlos Aparisi CanteroNo ratings yet
- Teori Idw Dari ArcgisDocument2 pagesTeori Idw Dari ArcgisrivaldiNo ratings yet
- Practical Journal (To All Department)Document71 pagesPractical Journal (To All Department)Israr AhmedNo ratings yet
- How To Find The Variance of Grouped Data (With ExDocument1 pageHow To Find The Variance of Grouped Data (With ExMakigh RigobertNo ratings yet
- Statistics Project - Final DraftDocument10 pagesStatistics Project - Final DraftShaurya ParnamiNo ratings yet
- Review 1 - Limits - Continuity (Pcalc+ To AP Calc)Document19 pagesReview 1 - Limits - Continuity (Pcalc+ To AP Calc)Titser LaarniNo ratings yet
- Data Mining For Business in Python DeckDocument93 pagesData Mining For Business in Python DeckCloudzoneNo ratings yet
- MA (Improper Integrals & Comparison Test For Improper Integrals)Document5 pagesMA (Improper Integrals & Comparison Test For Improper Integrals)John ManciaNo ratings yet
- SaadDocument460 pagesSaadsasanNo ratings yet
- Singularities ResiduesDocument7 pagesSingularities ResiduesLakshmanan SakthivelNo ratings yet
- Soal Tugas 1 Meh - Gasal - 2018-2019Document3 pagesSoal Tugas 1 Meh - Gasal - 2018-2019Archita Tandhi100% (2)
- Introduction To Complex NumbersDocument10 pagesIntroduction To Complex NumbersGANAPATHY.SNo ratings yet
- QM10 Tif Ch09Document24 pagesQM10 Tif Ch09Lour RaganitNo ratings yet
- The Logistic Regression Analysis in Spss - Statistics Solutions PDFDocument2 pagesThe Logistic Regression Analysis in Spss - Statistics Solutions PDFSajjad HossainNo ratings yet
- Laplace TableDocument2 pagesLaplace TableArdi Beskom GambargraphyNo ratings yet
- Name: Ahmed Abd Almagieed Bujbara Number: 211519205 Group: 1Document8 pagesName: Ahmed Abd Almagieed Bujbara Number: 211519205 Group: 1Amer HussainNo ratings yet
- 15ma207 Probability & Queueing Theory Maths 4th Semester Question Bank All Unit Question Paper 2017.v.srm - Ramapuram PDFDocument15 pages15ma207 Probability & Queueing Theory Maths 4th Semester Question Bank All Unit Question Paper 2017.v.srm - Ramapuram PDFUttam NeelapureddyNo ratings yet
- Additional Mathematics - Chapter 2: Quadratic EquationsDocument28 pagesAdditional Mathematics - Chapter 2: Quadratic EquationsnurazrreenNo ratings yet
- FP2C7 Maclaurin and Taylor SeriesDocument2 pagesFP2C7 Maclaurin and Taylor SeriesLoh Jun XianNo ratings yet
- Track BucklingDocument11 pagesTrack BucklingsennabiaaNo ratings yet
- Higher Order Sliding Mode Control: Capital University of Science and Technology, IslamabadDocument14 pagesHigher Order Sliding Mode Control: Capital University of Science and Technology, IslamabadOmar Zeb KhanNo ratings yet
- Statistical Inferences Assignment-2Document3 pagesStatistical Inferences Assignment-2NOORI KhanaNo ratings yet
- Calculus - Module 2.1 of Week 3 PDFDocument4 pagesCalculus - Module 2.1 of Week 3 PDFJimbo J. AntipoloNo ratings yet
- Complex Integration PDFDocument12 pagesComplex Integration PDFjayroldparcede100% (2)
- Ch.9 DifferentiationDocument1 pageCh.9 DifferentiationNikitha SomaratneNo ratings yet
- Integration by PartsDocument9 pagesIntegration by PartsMaria Jose de las mercedes Costa AzulNo ratings yet
- Pima Indians Diabetes Database Analysis - KaggleDocument37 pagesPima Indians Diabetes Database Analysis - KaggleAbhinav DegaNo ratings yet
- (1997) Normal-Boundary Intersection A New Method For Generating The Pareto Surface in Nonlinear Multicriteria Optimization ProblemsDocument27 pages(1997) Normal-Boundary Intersection A New Method For Generating The Pareto Surface in Nonlinear Multicriteria Optimization ProblemsJONATHAN JUSTINO APOS CASSIMIRONo ratings yet
- Impact of Organizational Culture On Employee Motivation WithDocument11 pagesImpact of Organizational Culture On Employee Motivation WithMohammad ElabedNo ratings yet
- Literature Review Process MappingDocument6 pagesLiterature Review Process Mappingelrurbrif100% (1)