Professional Documents
Culture Documents
Kinematics of CM 11 Convected Coordinates Rates
Uploaded by
sujayan2005Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Kinematics of CM 11 Convected Coordinates Rates
Uploaded by
sujayan2005Copyright:
Available Formats
Section 2.
11
Convected Coordinates: Time Rates of Change
In this section, the time derivatives of kinematic tensors described in §2.4-2.6 are now
described using convected coordinates.
2.11.1 Deformation Rates
Time Derivatives of the Base Vectors and the Deformation Gradient
First, the material time derivatives of the deformed base vectors are, from 2.10.8,
g& i = F& G i = F& F −1g i = −FF& −1g i
(2.11.1)
g i = F& −T G i = F& −T F T g i = −F −T F& T g i
with, again from 2.10.8,
F& = g& i ⊗ G i
F& −1 = G i ⊗ g& i
(2.11.2)
F& −T = g& i ⊗ G i
F& T = G i ⊗ g& i
The Velocity Gradient
The velocity gradient is defined by 2.5.2, l = grad v , so that, using 1.16.5,
∂v ∂v ∂v ∂Θ j ∂v
l= = i ⊗ ei = ⊗ ei = ⊗gj (2.11.3)
∂x ∂x ∂Θ ∂x
j i
∂Θ j
Also, from 1.16.3,
∂x& ∂v
g& i = = (2.11.4)
∂Θ i
∂Θ i
so that, as an alternative to 2.11.3,
l = g& i ⊗ g i (2.11.5)
This is consistent with Eqn. 2.5.4, F& = lF , which gives, with 1.11.2a and 2.10.8b,
( )( )
l = F& F −1 = g& i ⊗ G i G j ⊗ g j = g& i ⊗ g i (2.11.6)
Solid Mechanics Part III 296 Kelly
Section 2.11
The components of the spatial velocity gradient are
l ij = g i lg j = g i ⋅ g& j
l⋅ij = g i lg j = g i ⋅ g& j
(2.11.7)
l i⋅ j = g i lg j = g mj g i ⋅ g& m = g i ⋅ g& j
l ij = g i lg j = g i ⋅ g& j
Further, from 2.11.1, 2.11.2 and 2.11.5,
g& i = lg i g& i = −l T g i
(2.11.8)
= gilT = −g i l
Contracting the first of these with dΘ i leads to
g& i dΘ i = lg i dΘ i (2.11.9)
which is equivalent to 2.5.1, dv = ldx .
The Rate of Deformation and Spin Tensors
From 2.5.6, l = d + w . The covariant components of the rate of deformation and spin are
1 ⋅
2
( T
) 2
( m m
&
2
)
d ij = g i l + l g j = g i g m ⊗ g + g ⊗ g m g j = (g i ⋅ g j + g i ⋅ g j ) = g i ⋅ g j
1 1
&
1
& &
2
1
2
( ) 1
2
( 1
2
)
wij = g i l − l T g j = g i g& m ⊗ g m − g m ⊗ g& m g j = (g i ⋅ g& j − g& i ⋅ g j )
(2.11.10)
Solid Mechanics Part III 297 Kelly
You might also like
- Kuliah11 (No Baru) PDFDocument10 pagesKuliah11 (No Baru) PDFRIZALNo ratings yet
- Fractional ConvolutionDocument9 pagesFractional ConvolutionМаша МашаNo ratings yet
- 2 - Lattice GF For FCC-JournalDocument11 pages2 - Lattice GF For FCC-Journaljasad68No ratings yet
- Solutions Manual: VibrationsDocument19 pagesSolutions Manual: VibrationsanleNo ratings yet
- Interpolating PolynomialsDocument6 pagesInterpolating PolynomialsVarunKanaujiaNo ratings yet
- CH 10Document71 pagesCH 10Ipshita Ranjana100% (1)
- Solutions To Chapter 10 ProblemsDocument40 pagesSolutions To Chapter 10 ProblemsCarlos Alfredo H ChNo ratings yet
- Introduction To Binary SistemsDocument17 pagesIntroduction To Binary SistemsSergio NuñezNo ratings yet
- General Relativity: Theory of Gravity: Sarthak DuaryDocument16 pagesGeneral Relativity: Theory of Gravity: Sarthak DuarySarthakNo ratings yet
- 2.1 Principle of Virtual WorkDocument36 pages2.1 Principle of Virtual Workmohamed ahmedNo ratings yet
- CH 33 - Total SolutionsDocument26 pagesCH 33 - Total SolutionsyangxxxiiiNo ratings yet
- Settlement Response of Granular Fill Sof PDFDocument7 pagesSettlement Response of Granular Fill Sof PDFJuan Camilo PinedaNo ratings yet
- Dwnload Full Modern Physics For Scientists and Engineers 4th Edition Thornton Solutions Manual PDFDocument35 pagesDwnload Full Modern Physics For Scientists and Engineers 4th Edition Thornton Solutions Manual PDFamandawrightrwfdcombka100% (11)
- CH 11Document34 pagesCH 11Rebeca CremonezNo ratings yet
- Location of Interface Bose-Einstein Condensate Mixtures in Semi-Infinite Space Under Neumann Boundary ConditionDocument6 pagesLocation of Interface Bose-Einstein Condensate Mixtures in Semi-Infinite Space Under Neumann Boundary ConditionTiến Đạt TrầnNo ratings yet
- Boundary Dynamics of JT GravityDocument27 pagesBoundary Dynamics of JT GravityEmilio CuarteroNo ratings yet
- Optical Fiber Communications 4th Edition Keiser Solutions ManualDocument8 pagesOptical Fiber Communications 4th Edition Keiser Solutions Manualdrtonyberrykzqemfsabg100% (22)
- Modern Physics For Scientists and Engineers 4th Edition Thornton Solutions ManualDocument35 pagesModern Physics For Scientists and Engineers 4th Edition Thornton Solutions Manualvespersroyalist.mjdj100% (22)
- Course: B.Tech-II Subject: Engineering Mathematics II Unit-2 Rai University, AhmedabadDocument14 pagesCourse: B.Tech-II Subject: Engineering Mathematics II Unit-2 Rai University, AhmedabadSameer A.ANo ratings yet
- Dynamic Analysis of Manipulators: Newtonian Approach: Berke GürDocument30 pagesDynamic Analysis of Manipulators: Newtonian Approach: Berke GürOmar Seraj Ed-DeenNo ratings yet
- Shear Modulus of Soils under Cyclic LoadingDocument9 pagesShear Modulus of Soils under Cyclic LoadingCescyle CostaNo ratings yet
- Recrangular Pulse FTDocument21 pagesRecrangular Pulse FTSarbagya BuddhacharyaNo ratings yet
- MCE 366 System Dynamics, Spring 2010 Problem Set 1Document8 pagesMCE 366 System Dynamics, Spring 2010 Problem Set 1MartinRodriguezNo ratings yet
- On The Gauss-Newton Method: Ioannis K. ArgyrosDocument14 pagesOn The Gauss-Newton Method: Ioannis K. ArgyrosMárcioBarbozaNo ratings yet
- Chapter 2. Electrostatic II: NotesDocument29 pagesChapter 2. Electrostatic II: NotesreflectiondarkNo ratings yet
- Solution Manual Modern General Relativity by Guidry PDFDocument125 pagesSolution Manual Modern General Relativity by Guidry PDFEzz Hassan100% (3)
- Ballistic ConductionDocument13 pagesBallistic ConductionAnkan Das RoyNo ratings yet
- Phys2 Week2 Error AnalysisDocument9 pagesPhys2 Week2 Error AnalysisSahirNo ratings yet
- Preprints202211 0152 v1Document11 pagesPreprints202211 0152 v1Ayse KocmazNo ratings yet
- Chain RuleDocument8 pagesChain RuletxungoNo ratings yet
- Conservation Equations For Mass Momentum and EnergyDocument12 pagesConservation Equations For Mass Momentum and Energypuja kochNo ratings yet
- Conservation Equations For Mass Momentum and EnergyDocument12 pagesConservation Equations For Mass Momentum and Energypuja kochNo ratings yet
- Effect of Rotation on Buoyancy Driven ConvectionDocument7 pagesEffect of Rotation on Buoyancy Driven Convectiondeepti chanderNo ratings yet
- 2003 CILAMCE On The Visualization of Domain Results Boundary Element AnalysisDocument15 pages2003 CILAMCE On The Visualization of Domain Results Boundary Element AnalysisRemo Magalhães de SouzaNo ratings yet
- Assignment 4 1 The Brachistochrone Problem 2 Pendulum With Changing LengthDocument7 pagesAssignment 4 1 The Brachistochrone Problem 2 Pendulum With Changing LengthNian Ibne NazrulNo ratings yet
- Full Paper Pre1128actDocument7 pagesFull Paper Pre1128actlhphong021191No ratings yet
- Chemical Kinetics: Click Togoto The Table of ContentsDocument39 pagesChemical Kinetics: Click Togoto The Table of ContentsRivaldi Di CaprioNo ratings yet
- 1.2.3 The Fundamental Theorem of Calculus: A F B F X F DX X FDocument8 pages1.2.3 The Fundamental Theorem of Calculus: A F B F X F DX X FEverything What U WantNo ratings yet
- Griffiths Problems 07.17Document3 pagesGriffiths Problems 07.17Luis Alejandro García MoraNo ratings yet
- Web Appendix A.3: A.3 Solutions To Differential EquationsDocument3 pagesWeb Appendix A.3: A.3 Solutions To Differential EquationsMayaNo ratings yet
- Problem 3.29 PDFDocument1 pageProblem 3.29 PDFKauê BrittoNo ratings yet
- Chapter 2Document34 pagesChapter 2Hamza HussineNo ratings yet
- Welfare EconomicsDocument26 pagesWelfare EconomicsHimanshu RajNo ratings yet
- Chapter 2 - Gamma FunctionDocument9 pagesChapter 2 - Gamma FunctionHamza HussineNo ratings yet
- Strauss PDEch 2 S 4 P 2Document8 pagesStrauss PDEch 2 S 4 P 2Rudi JuliantoNo ratings yet
- Economics 712 Steven N. Durlauf Fall 2010Document13 pagesEconomics 712 Steven N. Durlauf Fall 2010dummy2011No ratings yet
- Laboratory 02Document12 pagesLaboratory 02JoJoMoNo ratings yet
- Mathematical Methods of Physics II: Solutions and Hints To Selected ExercisesDocument136 pagesMathematical Methods of Physics II: Solutions and Hints To Selected ExercisesaaaaaaaaaaaaaaaaaaaNo ratings yet
- Piv Ann3Document6 pagesPiv Ann3pipul36No ratings yet
- Gokce N 1996Document24 pagesGokce N 1996YEFERSON RAMIREZ OSCCONo ratings yet
- Chapter-2-REPRESENTATION OF CONTROL COMPONENTSDocument38 pagesChapter-2-REPRESENTATION OF CONTROL COMPONENTSMuhammad FadilNo ratings yet
- Chapters 1-11 Heat Transfer Numerical SolutionsDocument155 pagesChapters 1-11 Heat Transfer Numerical SolutionsAyush DeoreNo ratings yet
- Group Permutations Part 1Document3 pagesGroup Permutations Part 1mjhiraparaNo ratings yet
- General Mathematics: First Quarter-Module 5B Representing Real-Life Situations Using Exponential FunctionsDocument7 pagesGeneral Mathematics: First Quarter-Module 5B Representing Real-Life Situations Using Exponential FunctionsMae Kyla DaclesNo ratings yet
- 2009 SISC SD-transportDocument24 pages2009 SISC SD-transportDanail VassilevNo ratings yet
- Cini 1978Document3 pagesCini 1978XintingNo ratings yet
- Complex Moduli of Viscoelastic Composites-II. Fiber Reinforced MaterialsDocument11 pagesComplex Moduli of Viscoelastic Composites-II. Fiber Reinforced MaterialsKomal ChawlaNo ratings yet
- Tables of Coefficients for the Analysis of Triple Angular Correlations of Gamma-Rays from Aligned NucleiFrom EverandTables of Coefficients for the Analysis of Triple Angular Correlations of Gamma-Rays from Aligned NucleiNo ratings yet
- The Quick Access ToolbarDocument81 pagesThe Quick Access Toolbarsujayan2005No ratings yet
- A Guide To Writing Your First CFD Solver: Mark Owkes Mark - Owkes@montana - Edu June 2, 2017Document11 pagesA Guide To Writing Your First CFD Solver: Mark Owkes Mark - Owkes@montana - Edu June 2, 2017lefriyekh achrafNo ratings yet
- lec5Document5 pageslec5sujayan2005No ratings yet
- KumarasambhavaCantosI Vii SanskritCommentaryEnglishTranslationNotes MrKale1917Document385 pagesKumarasambhavaCantosI Vii SanskritCommentaryEnglishTranslationNotes MrKale1917tonyvinayakNo ratings yet
- Introduction To LabVIEWDocument118 pagesIntroduction To LabVIEWHerman HerklotzNo ratings yet
- C++ Basic Input-OutputDocument3 pagesC++ Basic Input-Outputsujayan2005No ratings yet
- IMSL Fortran Library User's Guide MATH/LIBRARY Volume 1 of 2Document947 pagesIMSL Fortran Library User's Guide MATH/LIBRARY Volume 1 of 2sujayan2005No ratings yet
- Heat Transfer Enhancement in a Tube with Double V-Ribbed Twisted-TapesDocument11 pagesHeat Transfer Enhancement in a Tube with Double V-Ribbed Twisted-TapesDavid QuevedoNo ratings yet
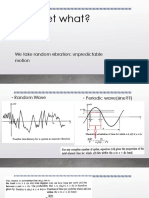
- Wavelet What?: We Take Random Vibration: Unpredictable MotionDocument18 pagesWavelet What?: We Take Random Vibration: Unpredictable Motionsujayan2005No ratings yet
- Schubert 2013-c GuideDocument10 pagesSchubert 2013-c Guidesujayan2005No ratings yet
- Fem NotesDocument205 pagesFem NotesYogesh ThakurNo ratings yet
- C++ Date and TimeDocument3 pagesC++ Date and Timesujayan2005No ratings yet
- Recent Comments: Home 01 Neet - Aipmt - Jee Main Mcqs Jee Main, Aipmt Mcqs Set 21Document4 pagesRecent Comments: Home 01 Neet - Aipmt - Jee Main Mcqs Jee Main, Aipmt Mcqs Set 21sujayan2005No ratings yet
- Titanium To Ss JointDocument5 pagesTitanium To Ss Jointsujayan2005100% (1)
- GOST 4543 71 Page 1 To 24Document26 pagesGOST 4543 71 Page 1 To 24JAFFER100% (1)
- Recent Comments: Home 01 Neet - Aipmt - Jee Main Mcqs Jee Main, Aipmt Mcqs Set 21Document4 pagesRecent Comments: Home 01 Neet - Aipmt - Jee Main Mcqs Jee Main, Aipmt Mcqs Set 21sujayan2005No ratings yet
- C++ Loop TypesDocument2 pagesC++ Loop Typessujayan2005No ratings yet
- 020Document5 pages020sujayan2005No ratings yet
- Microsoft Vs 2015 KeysDocument5 pagesMicrosoft Vs 2015 Keyssujayan2005No ratings yet
- PH36010 Numerical Methods: Solving Differential Equations Using MATHCADDocument32 pagesPH36010 Numerical Methods: Solving Differential Equations Using MATHCADbashasvuceNo ratings yet
- Recent Comments: Home 01 Neet - Aipmt - Jee Main Mcqs Jee Main, Neet Mcqs Set 20Document5 pagesRecent Comments: Home 01 Neet - Aipmt - Jee Main Mcqs Jee Main, Neet Mcqs Set 20sujayan2005No ratings yet
- Recent Comments: Home 01 Neet - Aipmt - Jee Main Mcqs Jee Main, Neet Mcqs Set 20Document5 pagesRecent Comments: Home 01 Neet - Aipmt - Jee Main Mcqs Jee Main, Neet Mcqs Set 20sujayan2005No ratings yet
- Delhi: Toxic Formalin Being Used To Preserve Fish: Follow Email AuthorDocument4 pagesDelhi: Toxic Formalin Being Used To Preserve Fish: Follow Email Authorsujayan2005No ratings yet
- UPCh 13Document34 pagesUPCh 13Alonso CamargoNo ratings yet
- Physics Question 4Document2 pagesPhysics Question 4sujayan2005No ratings yet
- Neutron Diffusion Theory - 2Document15 pagesNeutron Diffusion Theory - 2mehrsaNo ratings yet
- Ragheb-Neutron Cross Sections-2011 PDFDocument26 pagesRagheb-Neutron Cross Sections-2011 PDFsujayan2005No ratings yet
- Upch 14Document67 pagesUpch 14sujayan2005No ratings yet
- One Group Reactor Theory - 2Document28 pagesOne Group Reactor Theory - 2mehrsaNo ratings yet
- Multidimensional Reactor Systems in Diffusion Theory PDFDocument19 pagesMultidimensional Reactor Systems in Diffusion Theory PDFsujayan2005No ratings yet
- Chapter 8 The D and F Block ElementsDocument25 pagesChapter 8 The D and F Block Elementspriyanka kNo ratings yet
- Vigilohm IM10, IM20 User Manual PDFDocument60 pagesVigilohm IM10, IM20 User Manual PDFTomuta StefanNo ratings yet
- Anti InfectiveDocument9 pagesAnti InfectiveMae DoctoleroNo ratings yet
- Hytera SmartOne-1Document4 pagesHytera SmartOne-1KPP SPUTNo ratings yet
- TDS EU G-Energy X Hydro Bio EngDocument2 pagesTDS EU G-Energy X Hydro Bio EngАлексей ДэконNo ratings yet
- Notes On Cargo Work by Capt. Kyaw Mya OoDocument333 pagesNotes On Cargo Work by Capt. Kyaw Mya OoKyaw Mya Oo100% (1)
- Descriptive Text Purpose:: ( (: The Use of Adjectives and Compound AdjectivesDocument3 pagesDescriptive Text Purpose:: ( (: The Use of Adjectives and Compound AdjectivesEka Nur Laela Mar'atus SholikhaNo ratings yet
- Codigos HondaDocument25 pagesCodigos Hondamarquin84No ratings yet
- CisplatinDocument3 pagesCisplatinRicey MelegritoNo ratings yet
- Unit Ii BVPDocument24 pagesUnit Ii BVPCurious ManNo ratings yet
- Standard Data Formats For Analytical Systems: Status and ChallengesDocument1 pageStandard Data Formats For Analytical Systems: Status and ChallengeschatNo ratings yet
- Typhidot AssayDocument16 pagesTyphidot Assaychocoholic potchiNo ratings yet
- 3-XLTC Manual 16-12-2019Document24 pages3-XLTC Manual 16-12-2019Paulo BeltranNo ratings yet
- Miconium Ctac29: Quaternary Ammonium SaltDocument1 pageMiconium Ctac29: Quaternary Ammonium Saltanon_993394650No ratings yet
- Converting Metric Mass UnitsDocument9 pagesConverting Metric Mass UnitsAnonymous EvbW4o1U7No ratings yet
- Acrow GASS Aluminium Product GuideDocument8 pagesAcrow GASS Aluminium Product GuideTrần AlanNo ratings yet
- Kultura at Tradisyon NG Mga HAPONDocument1 pageKultura at Tradisyon NG Mga HAPONJullianMarkNo ratings yet
- Manual Ingersoll Rand 7 - 5 HPDocument188 pagesManual Ingersoll Rand 7 - 5 HPedgarescalante78100% (4)
- 10th Grade Vocabulary Matching ExerciseDocument2 pages10th Grade Vocabulary Matching ExerciseDinara İbrahim QızıNo ratings yet
- High Performance Epoxy Tile GroutDocument3 pagesHigh Performance Epoxy Tile GroutShaik J MohamedNo ratings yet
- Art Appreciation ReviewerDocument14 pagesArt Appreciation ReviewerRon RealinNo ratings yet
- Bubble Wrap Manufacturing ProcessDocument13 pagesBubble Wrap Manufacturing ProcessAnonymous a8rdyKOCNo ratings yet
- QAQC Objective & Key Career AchievementsDocument3 pagesQAQC Objective & Key Career Achievementssaffririzal4237100% (2)
- Jamaica Kincaid NotesDocument16 pagesJamaica Kincaid NotesDaniela Gomez RiveraNo ratings yet
- 3-What Causes WindDocument22 pages3-What Causes WindMadalina JogararuNo ratings yet
- 13 HD 120Document4 pages13 HD 120văn hiếu phanNo ratings yet
- Spare Parts List RieterDocument1 pageSpare Parts List RieterMd. Bulbul AhmedNo ratings yet
- English Class A1 + Present Simple Present Continuous Unit 1Document5 pagesEnglish Class A1 + Present Simple Present Continuous Unit 1agnieszka.bejsterNo ratings yet
- PCR COVID Test ReportDocument1 pagePCR COVID Test ReportBilly Jean BanucaNo ratings yet
- L-7 From Shelters To Village Settlements LPDocument29 pagesL-7 From Shelters To Village Settlements LPAvril FernandesNo ratings yet