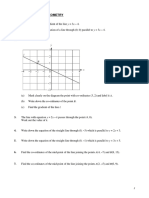
Relations, Functions and Graphs

Straight-line graphs

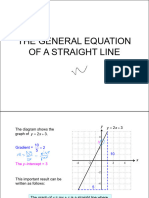
Graphs of the form y  mx  c

The equation of any straight-line graph can always be written in the form y  mx  c, where m is the
gradient and c is the y-intercept.
Line a has a gradient of _​ 2 ​ 2 (so m  2), and a y-intercept of 4.
4
y

Therefore its equation is y  2x  4. 4

Line b has a gradient of  ​ _4 ​  ​ _2 ​(so m   ​ _2 ​), and a y-intercept of 4.
2 1 1 b
3
Therefore its equation is y   ​ _ ​x  4.
1
2 a 4
2
Graphs of the form ax  by  c
1
The graph of 3x  4y  12 can be arranged to give y   ​ _4 ​x  3,
3

showing that it is a straight line with gradient  ​ _4 ​and y-intercept

3
x
–2 4
at 3. To sketch the graph of 3x  4y  12, substitute x  0, to get
the y-intercept of 3, and substitute y  0 to get the x-intercept of 4.

Other graphs

These graphs are often used to model real-life situations.

Quadratic graphs y  ax2  bx  c Solution of 0  ax2  bx  c
Parabolas y
y y Roots are
a>0 a<0 x � p or
y � ax 2 � bx � c
x�q

p q x
x x
a
Cubic graphs y  ax3  bx2  cx  d Reciprocal graphs y  ___
​   ​
x
y y y y
a>0 a<0
a>0 a<0

x x x x

Distance/Speed time graphs

Distance–time graphs
Gradient of slope  speed
A B
10
Velocity
Distance (m)

10
Gradient OA  ___
​   ​  5 m/s
2
0
Gradient AB  ​ __  ​ 0 m/s C
4 O 2 6 11
10
Gradient BC   ​ ___ ​  2 m/s Time (s)
5

Relations, Functions and Graphs 1

 Speed–time graphs
Gradient of slope  acceleration
Area under graph  distance travelled
Acceleration A B
10
10
Gradient OA  ___
​   ​  5 m/s2 (speeding up)
2

Speed (m/s)
0
Gradient AB  __
​   ​   0 m/s2 (constant speed)
3
10 C
Gradient BC   ​ ___ ​  2.5 m/s2 (slowing down) O 2 5 9
4
Time (s)
Average speed
_ 1
​ 2 ​ (3  9)  10
distance travelled _______________
Average speed  _______________  6​ _3 ​ m/s
2
​   ​
      ​   ​
    
time 9

Simultaneous equations

To solve simultaneous equations graphically

• Draw the graphs for both equations on one set of axes.
• The solution is at the intersection points of the graphs.
• If the graphs don’t intersect, there is no solution.
• If the graphs are the same, there are an infinite number of solutions.
Solve the simultaneous equations y
2x – y � 0
x  y  6, 2x  y  0 6

Solution is x  2, y  4. 4 Solution point, x � 2, y � 4

x�y�6

2 6 x
0

Simultaneous inequalities

Inequalities can be shown graphically by shading regions to identify solutions in unshaded regions.
Solve the inequalities x  0, y  0, x  y  3 and y < 2 by drawing suitable lines (solid or broken) and
shading unwanted regions.
The solid line means that solutions
can lie on the line (x � y � 3)
y

3
y�2
2
The broken line means
that the solution cannot
Solutions lie on the line (y < 2)
in this x
region 0 3
x�y�3

2 Relations, Functions and Graphs

Linear programming

Linear programming involves taking linear inequalities describing a problem and finding the ‘best’
solution. This is done by graphing the inequalities to find the region on the x-y plane that satisfies the
inequalities, then finding the ‘best’ solution which is at or near a vertex of this region.
Example 1.
Kalisa has two crops, A and B, to plant in a 6 hectare field. A takes 1 hour per hectare to plant, B takes
2 hours per hectare to plant and the planting must take no longer than 8 hours.
The profit from A is $3000 per hectare, while the profit from B is $4000 per hectare.
What is Kalisa’s maximum profit?
Let x be the number of hectares of A planted, x > 0. y
8
Let y be the number of hectares of B planted, y > 0.
7
The field is 6 acres ⇒ x 1 y < 6
6
x hectares of A takes x hours to plant. x�y�6
5
y hectares of B takes 2y hours to plant.
4
Only 8 hours are available ⇒ x 1 2y < 8
3
These inequalities are shown on the graph where the solution
2
set is un-shaded. x � 2y � 8
1
The profit is given by 3000x 1 4000y.
The maximum profit will occur at a vertex of the solution set. –1 0 1 2 3 4 5 6 7 8 x
–1
These vertices are (0, 0), (0, 4), (4, 2), (6, 0)
Substituting these values shows that (4, 2) gives the maximum profit of $20 000
So Kalisa should plant 4 hectares of A and 2 hectares of B to give a profit of $20 000
Example 2.
A company has to move 16 large crates. A van can take 1 crate, while a lorry can take 4 crates. There are
8 drivers available. The cost of using a van is $300 while the cost of using a lorry is $1400. What is the
minimum cost of moving the crates?
Let x be the number of vans used, x > 0 y
Let y be the number of lorries used, y > 0 12

The number of drivers available is 8 ⇒ x 1 y < 8

x vans will move x crates. 10
y lorries will move 4y crates.
16 crates must be moved ⇒ x 1 4y > 16 8
These inequalities are shown on the graph where x�y�8
the solution set is un-shaded. 6
The cost is given by 300x 1 1400y
Because x and y must both be integers, the minimum 4
cost will occur at or near a vertex of the solution set.
x � 4y � 16
These points are (0, 4), (0, 8), (4, 3), (5, 3) 2
Substituting these values shows that (4, 3) gives the
minimum cost of $54 000. 0 2 4 6 8 10 12 x
So the firm should use 4 vans and 3 lorries at a cost
of $54 000.

Relations, Functions and Graphs 3

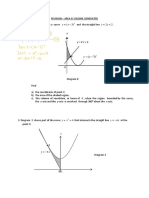
 Graphs

Solution of equations
• To solve simultaneous equations graphically, draw both graphs on one set of axes.
The co-ordinates of the intersection points are the solutions of the simultaneous equations.
To find roots of ... Draw graphs ... Roots are intersection points ...
d  ax2  bx  c y  ax2  bx  c y
yd

p 0 q x

x � p or q

x  d  ax2  bx  c y  ax2  bx  c y
yxd

p 0 x
q

x � p or q

cx  d  ax3  bx2 y  ax3  bx y

y  cx  d
p q
0 r x

x � p, q or r

Gradients of curves

Estimating gradients of curves

The gradient of a curve at a point P can be estimated by drawing the best-fitting y
tangent to the curve by eye, then finding the gradient of this line, using
‘rise’ P
Gradient  _____
​    ​ rise
‘run’
run

0 x

4 Relations, Functions and Graphs

 Relations

Sets are often related to each other. The relationship can be shown in many ways:
a A headed table b A mapping diagram using sets

Child Father Nathan Grant

Nathan Kavi Wilma Calvin
Puteri Calvin
Maisie Elton
Maisie Elton
Child Father

c A table d Ordered pairs

22 0 (22, 0), (21, 1), (0, 2), (1, 3)

21 1
0 2
1 3

e A mapping diagram using number lines f A graph

�3 �2 �1 0 1 2 3
y
5
4

�3 �2 �1 0 1 2 3 3
y�x�2
2
1

�3 �2 �1 0 1 2 3 x
�1
�2

g A box diagram h An algebraic relationship

x x�2
Add 2 to input
y5x12

Relationships can be of different types.

�3

�2 0 �2
Fish 0 0
�1 1 �1
Dog 1 1
0 2 Amber 0
Bird 2 4
1 3 Max Jodie 1
Cat 3 9
2 4 Lara Deval 2
Human 4
x x�2 Otis 3
Animal Number
of legs Child Parent x x

‘one to one’ ‘many to one’ ‘many to many’ ‘one to many’

Relations, Functions and Graphs 5

 Functions

‘One to one’ and ‘many to one’ relations are called functions.

If a vertical line placed anywhere on a graph of a relationship intersects the graph at only one point
then the relationship is a function.
y y
4 4

y
3 3 2

2 2 1

1 1 x
–1 0 1 2 3

x x –1
–1 0 1 2 3 –1 0 1 2 3

–1 –1 –2
Function Function Not a function
• The domain of a function is the set of numbers the function can use.
1
The domain of f(x)  __​   ​  is all real numbers except zero.
x

Range
(Division by zero is not allowed.)

Domain

y � 1x

• The range of a function is the set of numbers produced by the function.

The range of the function f(x)  x2 is {y: y  0, y a real number}. Range
(Any number squared is always positive.)
• The inverse function f1(x), undoes whatever the function has done.
The inverse of f(x)  x  3 is f1(x)  x  3. Domain

To find the inverse function: y � x2

Write the function as y  ...
Change any x to y and any y to x. y

Make y the subject, giving the inverse function. y�x

• gf(x) is a composite function. gf(x) means

3
‘do f followed by g’.
f �1 (x) � x � 3
If f(x)  x2 and g(x)  x  2, then
gf(x)  x2  2 (do f first then g) 0 x
2
fg(x)  (x  2) (do g first then f) f (x) � x � 3
• Inverse of a composite functions. (gf)1  f1g1.
�3

If f(x)  f1(x) then the functions are self inverse.

6 Relations, Functions and Graphs