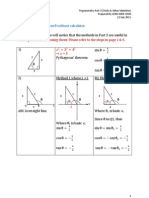
Trigonometry Part 4 (Solution of Triangle) Prepared by LENG KIEN YUEN 12 July 2011

Solution of Triangle Concepts below and Basic ratios in Part 1 are widely used (Especially Physics, Vector & 3D questions)! Please make sure you can understand them very well! Sine Rule
A

in

in

in

Notice that the ratio consists of sides and opposite angle. Normally it is used in pair. Find an opposite angle when 2 sides with a oppo ite are given. Find a ide when 2 oppo ite with a ide are given. It can be proven by dividing the triangle into 2 right triangle and use in . Try it!! It has a weakness. Let find it out!

Cosine Rule
A

2
C

co

C i alway the oppo ite of ide c. While ide a and b are adjacent to C. Find an when 3 sides are given Find a ide when 2 ide and an are given. Does this formula look familiar?

Note: The e 2 rule are u ed to olve interior and ide problem in TRIANGLE.

Trigonometry Part 4 (Solution of Triangle) Prepared by LENG KIEN YUEN 12 July 2011

Question ABC is a triangle. AB = 12 units, AC = 8 units, and BC = 7 unit . ABC 39.838. Find ACB. Strategy
A

12

Find

39.838 7 C

Sine Rule? or Cosine Rule? Sine Rule We have 2 sides and a opposite angle OK Cosine Rule We have 3 ide OK However, Co ine Rule formula i more complicated or longer. I personally prefer Sine Rule because it is simple. For practice purpose, we use both rules.

Solution Sine Rule 8 in 39.838 in ACB 2 in ACB 2 8 in 39.838

Cosine Rule 2 8 2 8 2 8 2 8 8 co ACB

co ACB

in ACB 0.960929 ACB 73.93

co ACB .2 ACB 106.07

The answer for both rules should be the same. What is wrong? Hints : 1. Observing the value of in ACB and co ACB. Which quarter does ACB belongs? Refer to ASTC in Part 2. 2. Observing the ACB result from both rules. What is the relationship between them? (Add them together) 3. Do we miss something when computing ACB from in ACB? 4. What is the actual diagram of this triangle?

Trigonometry Part 4 (Solution of Triangle) Prepared by LENG KIEN YUEN 12 July 2011

Note: It is the weakness of Sine Rule as it may give 2 different solutions to triangle. Since in > , then the i in Q and Q2. You have to determine which i correct! How? While Cosine rule always gives correct solution. Which rule is better in finding an when 3 ide are given? Question ABC i a triangle. AB 2 unit and AC 8 unit . ABC ACB. (It is SSA case!)(Without BC = 7 units) Strategy
A

39.838. Find

12

Find

39.838 C

Sine Rule? or Cosine Rule? Sine Rule We have 2 sides and a opposite angle OK Cosine Rule We have 2 ide po ible by using it twice. (Difficult) Try it yourself! It should have the same solution as Sine Rule.

Solution Sine Rule 8 in 39.838 in ACB 2 in ACB 2 8 in 39.838

When ACB 106.07 BAC 34.092 BC = 7

A 66.232 34.092 12 8 39.838 B 7 106.07 C 11.43 73.93 C 8

in ACB 0.960929 ACB 73.93 or 106.07 When ACB 73.93 BAC 66.232 BC = 11.43

Trigonometry Part 4 (Solution of Triangle) Prepared by LENG KIEN YUEN 12 July 2011

Ambiguous Triangle (Cause of Ambiguous Cases of Sin Rule)

A

b a in ABC

Given a triangle ABC, all of the following conditions will need to be fulfilled for the case to be ambiguous (2 possible solutions for Sine Rule): Only ABC and the sides a and b are known or given. ABC < 90 a>b b > a in ABC Area of Triangle
A

Area We are looking from C Height Ba e b in C a where in C

= ab in C
B a C

Then we look from A and B and group all of them, then we have following equation. Area ab in C ac in B bc in A Notice that each formula contain a, b and c while the angle use is always between 2 sides.

Little Knowledge Formula above can be used to prove Sine Rule. Just multiply and divide with something. Try it!! In circular measures, does r in look similar?