Kyle Brunner, Kari Cook, Sarah Purcell, Dr. Larry Baxter, Dr. William Hecker, and Dr.

Vincent Wilding

Linear versus Nonlinear Regression

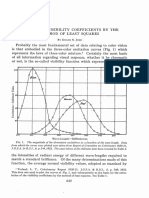
Introduction: A comparative analysis of linear and nonlinear regression of Arrhenius kinetic data with ko of 1019 s-1 and Ea/R of 17600 K. Data error was simulated using 2% noise. Linear Regression
46 44 42

Confidence Region

Equation:

Ea 1 ln(k ) = ln(k o ) + R T

40 ln(k0) ln(1/s))

Confidence Regions of Linear and Nonlinear Analysis for Comparison

Confidence Regions of Linear and Nonlinear Analysis for Comparison:

An Example with Optimal Experimental Design

38

36

Minimized:

(ln(k ) ln(k ))
i

34 32

i2

30 1.30E+04 1.40E+04 1.50E+04 1.60E+04 1.70E+04 1.80E+04

E/R (K)

A comparative analysis of linear and nonlinear regression of Arrhenius kinetic data with ko of 1019 s-1 and Ea/R of 17620 K. Data error was simulated using 2.3% noise.
8E+19
k0 (1/s) 7E+18 5E+18 3E+18 1E+18

Independent Variable:

1 T
95% CI (+/-) 3.632 1350 Parameter Value 2.782*1016 15630 Actual Value

The figure above shows the elliptical confidence region from the linear regression ln(ko) vs. EA/R. This confidence region was modified below to be ko vs. EA/R.
7E+18

6E+19

4.5E+19

k 0 (1 /s ))

Regressed Regressed Parameter Form Value

-1E+18 14000

15000

16000 E/R (K)

17000

18000

4E+19 3.5E+19 3E+19

4E+19

k0 (1/s)

k0 (s-1) EA/R (K)

ln(k0)

37.865 15630

1019 17600

5E+18 3E+18 1E+18 -1E+18 14000

k0 (1/s)

EA/R

2E+19
2.5E+19 2E+19 1.5E+19 1E+19

For several reasons, using the traditional linear regression biases data towards low temperatures.

0
15000 16000 E/R (K) 17000 18000

-2E+19 1.60E+04 1.65E+04 1.70E+04 1.75E+04 1.80E+04 1.85E+04

5E+18 16000

E/R (K)

1.60E+04 1.65E+04 1.70E+04 1.75E+04 1.80E+04 1.85E+04 1.90E+04 1.95E+04 2.00E+04 2.05E+04 2.10E+04

Nonlinear Regression
Equation:

E/R (K)

Ea k = ko exp R T

Confidence Region
The figure above illustrates two main points:
8E+19

Minimized:

(k k )
i

The figure above illustrates three main points: Optimal design reduces linearization bias. The confidence region for the nonlinear regression (red region) is much smaller than that of the linear regression (blue region). Approximate confidence intervals (shaded boxes) give an over simplified representation of the reasonable range of values for a given parameter. The majority of the areas covered by the confidence intervals for both the linear and nonlinear regressions lie outside of the respective confidence regions.

i2

6E+19

The confidence region for the linear regression (red region) barely overlaps that of the nonlinear regression (black region). Neither of the regressions confidence regions include the best estimate of the parameters for the other analysis (shown as the red and blue points). Note: The difference of 3 orders of magnitude between the ko best estimates makes the confidence region of the linear regression smaller. The relative size, normalized to the magnitude of the parameter estimate, is larger.

Independent Variable: Regressed Form

T
Regressed Value 1.282*1019 17700 Actual Value 1019 17600

k 0 (1/s))

4E+19

2E+19

Parameter

-2E+19 1.60E+04 1.65E+04 1.70E+04 1.75E+04 1.80E+04 1.85E+04 E/R (K)

k0 (s-1) EA/R (K)

k0 EA/R

Summary and Conclusions: The results from linear and nonlinear regression are different. The linear regression introduces biases into the analysis and ignores the interactions between the parameters. As a result, the parameter estimates can be orders of magnitude off. Using nonlinear regression is a sure way to get reasonable parameter best estimates and confidence regions.