UNIDAD # II: DERIVACIN EN EL CAMPO COMPLEJO

DEFINICIN DE DERIVADA. Sea f una funcin cuyo dominio contiene un entorno Z0 , la derivada
de f(z) se define como:
z
z
z z
z f z f
Lim z f

) ( ) (
) (
0
FUNCIONES ANALTICAS.
Si la derivada ) (z f
existe en todo punto Z de una regin , entonces decimos que f(z) es
analtica en . Una funcin f(z) es analtica en un punto Z0 , si existe una vecindad
0
Z Z
< , tal
que en cada punto de ella ) (z f
exista.
ECUACIN DE CAUCHY RIEMANN.
Una condicin necesaria para que w = f(z) = u(x,y) + iv(x,y) sea analtica en una regin es
decir, en u y v satisfacen las ec. de Cauchy Riemann


y
v
x
u

;
x
v
y
u

y x
v u
;
x y
v u
Ec. 1
Si las derivadas anteriores son continuas en , entonces las ec. de Cauchy Riemann son
condiciones suficientes para que f(z) sea analtica en . Las funciones u(x,y) y v(x,y) son llamadas
algunas veces funciones conjugadas.
Teorema: Supongamos que f(z) = u(x,y) + iv(x,y) y que f(z) existe en un punto z0 . Entonces las
primeras derivadas parciales de u y v deben existir en ese punto y debe satisfacer en l las ec. de
Cauchy Riemann.
y x
v u
;
x y
v u

Condiciones suficientes: El que las ec. de Cauchy Riemann se satisfagan en un punto z0 no basta para
asegurar la existencia de la derivada de una funcin f(z) en ese punto. Pero con ciertos requisitos de
continuidad se tiene el siguiente teorema:
Sea la funcin f(z) = u(x,y) + iv(x,y) definida en algn entorno de un punto Z0 = x0 + y0.
Supongamos que las derivadas parciales satisfacen la ec. de de Cauchy Riemann.
y x
v u
;
x y
v u
, en ( x0 + y0 ) la derivada de f(z) existe.
FUNCIONES ARMNICAS.
Si las segundas derivadas de u y v con respecto a x y y , existen y son continuas en una regin
, entonces deducimos de la ec. 1 que:
0
2
2
2
2

y
u
x
u
;
0
2
2
2
2

y
v
x
v
Ec. de Laplace
Funciones tales como u(x,y) y v(x,y) las cuales satisfacen la ec. de Laplace en una regin ,
son llamadas funciones armnicas de
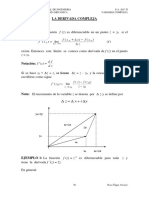
INTERPRETACIN GEOMTRICA DE LA DERIVADA.
Sea Z0 un punto en el plano Z y sea w0 su imagen P en el plano w bajo la transformacin
w = f(z) . Ya que suponemos f(z) unvoca , el punto Z0 es aplicado slo en un punto w0.
PLANO Z PLANO W
Q
y v
Q
w = f(z0 + z) f(z0)
x0 +z z
P P
x0 w0 = f(z0)
x u
Figura N 1 Figura N 2
Si incrementamos Z0 en z obtenemos el punto Q de la fig N 1. Este punto tiene como imagen a Q
en el plano W. En la fig N 2 vemos que PQ representa el numero complejo w = f(z0 + z) f(z0) .
Se deduce que la derivada en Z0 esta dada por:
QP
P Q
Lim
z f z f
Lim
P Q
z
z
z
' ' ) ( ) (
0 0
0

+


W0 + w = f( z0
+ z)
DIFERENCIALES. Sea la funcin f definida en el campo complejo, se dice que f es diferenciable
en Z0 cuando existe su derivada en dicho punto.
REGLAS DE DIFERENCIACIN.
Si f(z) , g(z) y h(z) son funciones analticas de Z , las siguiente reglas de diferenciacin son
validas.
1.- [ ] ) ( ) ( ) ( ) ( z g z f z g z f Dx t t
2.- [ ] ) ( . ) ( . z f C z f C Dx , C = constantes
3.- [ ] ) ( ). ( ) ( ). ( ) ( ). ( z f z g z g z f z g z f Dx +
4.-
( )
2
) (
) ( ). ( ) ( ). (
) (
) (
z g
z g z f z f z g
z g
z f
Dx

1
]
1

, g(z) 0
5.- Regla de la cadena para diferenciacin de funciones compuestas.
w = f(z) y W = g(w) de modo que W = F(z) , entonces
dz
dw
dw
dW
dz
dW
.
OPERADORES DIFERENCIALES COMPLEJOS.
Consideremos F(x,y) como una funcin real continuamente diferenciable de x y y , mientras
) , ( ) , ( ) , ( y x iQ y x P y x A + es una funcin compleja continuamente diferenciable de x y y.
(vectorial). En trminos de las coordenadas conjugadas:
) , (
2
,
2
) , ( Z Z G
i
Z Z Z Z
F y x F

,
_ +
y ) , ( ) ( Z Z B Z A
El operador nos lleva a definir las siguientes operaciones:
1. Gradiente: Definimos e gradiente de una funcin real F (escalar) por:

y
F
i
x
F
F gradF

Similarmente, el gradiente de una funcin compleja A = P + iQ (vectorial) esta definida por:

,
_

x
Q
y
P
i
y
Q
x
P
A gradA
en particular si B es una funcin analtica de Z , el = 0
2. Divergencia : Definimos la divergencia de una funcin compleja (vectorial) por:

y
Q
x
P
A divA

.
La divergencia de una funcin real o compleja (escalar o vectorial) es siempre una funcin real
(escalar)
3. Rotacional:
y
P
x
Q
xA RotA

4. Laplaciano: Esta definida como el producto escalar de consigo mismo, es decir:

z z y x

.
4 .
2
2
2
2
2
2
. Si A es analtica,
0 .
2
A
as que
0
2
P
y
0
2
Q , es decir P y Q son armnicas
Algunas identidades donde intervienen gradiente, rotacional y divergencia.
Las siguientes identidades son validad si A1 , A2 y A son funciones diferenciales:
( )
2 1 2 1
A A A A + +
( )
2 1 2 1
divA divA A A div + +
( )
2 1 2 1
RotA RotA A A Rot + +
( )
2 1 2 1 2 1
. . . A A A A A A +
0 ) ( A Rot , si A es real, es decir Im(A) es armnica
0 ) ( A div , si A es imaginaria, es decir Re(A) es armnica