Chapter 11

Frequency Response
Analysis
Overall Course Objectives
Develop the skills necessary to function as
an industrial process control engineer.
Skills
Tuning loops
Control loop design
Control loop troubleshooting
Command of the terminology
Fundamental understanding
Process dynamics
Feedback control
Frequency Response Analysis
Is the response of a process to a sinusoidal
input
Considers the effect of the time scale of the
input.
Important for understanding the propagation
of variability through a process.
Important for terminology of the process
control field.
But it is NOT normally used for tuning or
design of industrial controllers.
Process Exposed to a Sinusoidal
Input
c(t)
y
s
(t)
G
p
(s)
Key Components of Frequency
Response Analysis
Time
a
c
a
y
y
s
c
A
t
p
360
2

A
= =
t
e
|
p
c
y
r
t
a
a
A
Effect of Frequency on A
r
and |
Time
c
y
s
A
t
p
Time
c
A
t
p
Bode Plot: A Convenient Means
of Presenting A
r
and | versus e
0.01
0.1
1
10
0.01 0.1 1 10 100
e
A
r
Ways to Generate Bode Plot
Direct excitation of process.
Combine transfer function of the process
with sinusoidal input.
Substitute s=i e into G
p
(s) and convert into
real and imaginary components which yield
A
r
(e) and |(e).
Apply a pulse test.
Developing a Bode Plot from the
Transfer Function
( )
(

=
+ =
+ =

) (
) (
tan ) (
) ( ) ( ) (
) ( ) (
1
2 2
e
e
e |
e e e
e e e
R
I
I R A
I i R i G
r
p
Derivation of the Bode Plot for a
First Order Process
) ( tan ) (
1
1
) (
1 1
) (
ation rationaliz After
1
) (
1
) (
1
2 2
2 2
2 2 2 2
2 2 2 2
p
p
p
p
p p p
r
p
p p
p
p
p
p
p
p
p
p
p
K
K K
A
K
i
K
i G
i
K
i G
s
K
s G
et e |
t e
t e
t e
e
t e
t e
t e
e
et
e
t
=
+
=
+
+
=
+

+
=
+
=
+
=

Properties of Bode Plots

) ( ) ( ) ( ) ( ) (
) ( ln ) ( ln ) ( ln ) ( ln )] ( ln[
or
) ( ) (
) ( ) (
) ( ) (
) ( ) (
) ( : Consider
e e e e e |
e e e e e
i G i G i G i G
i G i G i G i G A
s G s G
s G s G
A
s G s G
s G s G
s G
d c b a
d c b a r
d c
b a
r
d c
b a
p
Z Z Z + Z =
+ =
=
=
Bode Plot of Complex Transfer
Functions
Break transfer function into a product of
simple transfer functions.
Identify A
r
(e) and |(e) of each simple
transfer function from Table 8.1.
Combine to get A
r
(e) and |(e) for complex
transfer function according to properties.
Plot results as a function of e.

Example of a Bode Plot of a
Complex Transfer Function
| |
( ) ( )
(
(

=
+
=
(
(

+ +
= =
(

+
+ +
=

2 2
1
2
2
2 2
2 2
2 2
1
2
tan
2 1
1 2
2
360
1
1
1
1 2
) (
p
p
p p
p
r
p p
p
r
s
I
c
p p
s
p
p
K
A
s s
K
A e
s
K
s s
e K
s G
t e
, et
|
, et t e
, t t
t
e u |
t , t t
u
u
Example Continued
( ) ( )
(

+
(
(

+
|
.
|

\
|
=
+
+
=
|
|
.
|

\
|

= + =
(

|
|
.
|

\
|
+

I p
p
I
p p
c p
r
I I
c r
I
c
K K
A
K A
s
K
t e t e
, t e
t
e u |
t e
, t e t e
t e
|
t e t
1
tan
1
2
tan
2
360
1
1
2 1
: process overall For
1
tan
1
1
1
1
1
2 2
1
2 2
2
2
2 2
1
2 2
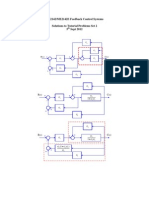
Bode Stability Criterion
Y
sp
(s)
Y(s)
G
p
(s)
Y
s
(s)
G
c
(s) G
a
(s)
-
+
G
s
(s)
Y
sp
(s)
Y(s)
G
p
(s)
Y
s
(s)
G
c
(s) G
a
(s)
-
+
G
s
(s)
Bode Stability Criterion
A system is stable if A
r
is less than 1.0 at the
critical frequency (i.e., e that corresponds
to |=-180)
Closed loop stability of a system can be
analyzed by applying the Bode Stability
Criterion to the product of the transfer
functions of the controller and the process,
i.e., G
c
(s)G
p
(s).
Gain Margin
0.01
0.1
1
10
0.01 0.1 1 10 100
e
A
r
M
Gain Margin
Gain Margin = 1/A
r
*
Where A
r
* is the amplitude ratio at the critical
frequency.
Controllers are typically designed with gain
margins in the range of 1.4 to 1.8 which implies
that A
r
at the critical frequency varies between
0.7 and 0.55, respectively.
Phase Margin
0.0001
0.001
0.01
0.1
1
10
0.01 0.1 1 10 100
e
A
r
eco
Phase Margin
PM = |- (180)
Where |* is | at the crossover frequency.
Controllers are typically designed with a PM
between 30 to 45.
Tuning a Control from the Gain
Margin
r
1
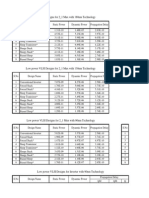
Problem: Determine for a gain margin equal 1.7 for a FOPDT
process ( 2, 3, 1.5).
Solution: From Table 8.1, one can determine A
and . First, determine such that 180
180 tan ( 3 ) 85.9
By trail and error,
c
p p p
K
K t u
| e |
e e
e

= = =
=
=

r
* 2
r
1.218 radians per unit time
Rearranging the equation for A ,
A 9 1
1.12
2
c
K
e
=
+
= =
Tuning a Control from the Phase
Margin
Phase margin determines the phase angle at
the crossover frequency.
The amplitude ratio at the crossover
frequency is one; therefore, the controller
gain can be calculated from the equation for
the amplitude ratio.
Example of a Pulse Test
y
s
c
Time
Developing a Process Transfer
Function from a Pulse Test
(

=
+ =
+

=
+
+
=
'
=
'
=
'
=
'
=

} }
} }
) (
) (
tan ) (
) ( ) ( ) (
) ( ) (
) ( ) ( ) ( ) (
) (
) ( ) (
) ( ) ( ) ( ) (
) (
sin ) ( ) ( cos ) ( ) (
sin ) ( ) ( cos ) ( ) (
1
2 2
2 2
2 2
0 0
0 0
e
e
e |
e e e
e e
e e e e
e
e e
e e e e
e
e e e e
e e e e
R
I
I R A
D C
C B D A
I
D C
D B C A
R
dt t t c D dt t t c C
dt t t y B dt t t y A
r
s s
Limitations of Transfer Functions
Developed from Pulse Tests
They require an open loop time constant to
complete.
Disturbances can corrupt the results.
Bode plots developed from pulse tests tend
to be noisy near the crossover frequency
which affects GM and PM calculations.
Nyquist Diagram
Real Axis
I
m
a
g
i
n
a
r
y

A
x
i
s |
A
r
Nyquist Diagram
(Complex Plane Plot)
( ) cos
( ) sin
Therefore, you can use the same
equations used to develop a Bode
plot to make a Nyquist diagram.
r
r
R A
I A
e |
e |
=
=
Nyquist Stabilty Criterion
Real Axis
I
m
a
g
i
n
a
r
y

A
x
i
s
0
0
2
2
-2
-2
(-1,0)
.
unstable
stable
Closed Loop Frequency
Response
Y
sp
(s)
Y(s)
G
p
(s)
Y
s
(s)
D(s)
+
+
G
c
(s) G
a
(s)
-
+
G
s
(s)
G
d
(s)
Example of a Closed Loop Bode
Plot
0
0.4
0.8
1.2
0.01 0.1 1 10 100
e
A
r
e
pf
Analysis of Closed Loop Bode
Plot
At low frequencies, the controller has time to
reject the disturbances, i.e., A
r
is small.
At high frequencies, the process filters
(averages) out the variations and A
r
is small.
At intermediate frequencies, the controlled
system is most sensitive to disturbances.
Peak Frequency of a Controller
The peak frequency indicates the frequency
for which a controller is most sensitive.
Overview
Understanding how the frequency of inputs
affects control performance and control
loop stability is important.
The analytical aspects of frequency
response analysis are rarely used
industrially.