Professional Documents
Culture Documents
Slides Prepared by John S. Loucks St. Edward's University: 1 Slide © 2003 Thomson/South-Western
Uploaded by
HRish BhimberOriginal Description:
Original Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Slides Prepared by John S. Loucks St. Edward's University: 1 Slide © 2003 Thomson/South-Western
Uploaded by
HRish BhimberCopyright:
Available Formats
Slides Prepared by JOHN S. LOUCKS St.
Edwards University
2003 Thomson/South-Western
Slide 1
Chapter 6 Continuous Probability Distributions
Uniform Probability Distribution Normal Probability Distribution Exponential Probability Distribution f(x)
2003 Thomson/South-Western
Slide 2
Continuous Probability Distributions
A continuous random variable can assume any value in an interval on the real line or in a collection of intervals. It is not possible to talk about the probability of the random variable assuming a particular value. Instead, we talk about the probability of the random variable assuming a value within a given interval. The probability of the random variable assuming a value within some given interval from x1 to x2 is defined to be the area under the graph of the probability density function between x1 and x2.
2003 Thomson/South-Western
Slide 3
Uniform Probability Distribution
A random variable is uniformly distributed whenever the probability is proportional to the intervals length. Uniform Probability Density Function f(x) = 1/(b - a) for a < x < b =0 elsewhere where: a = smallest value the variable can assume b = largest value the variable can assume
2003 Thomson/South-Western
Slide 4
Uniform Probability Distribution
Expected Value of x
E(x) = (a + b)/2
Variance of x Var(x) = (b - a)2/12 where: a = smallest value the variable can assume b = largest value the variable can assume
2003 Thomson/South-Western
Slide 5
Example: Slater's Buffet
Uniform Probability Distribution Slater customers are charged for the amount of salad they take. Sampling suggests that the amount of salad taken is uniformly distributed between 5 ounces and 15 ounces. The probability density function is f(x) = 1/10 for 5 < x < 15 =0 elsewhere where: x = salad plate filling weight
2003 Thomson/South-Western
Slide 6
Example: Slater's Buffet
Uniform Probability Distribution for Salad Plate Filling Weight f(x)
1/10 x 5 10 15 Salad Weight (oz.)
2003 Thomson/South-Western
Slide 7
Example: Slater's Buffet
Uniform Probability Distribution What is the probability that a customer will take between 12 and 15 ounces of salad? f(x) P(12 < x < 15) = 1/10(3) = .3 1/10 x 5 10 12 15 Salad Weight (oz.)
2003 Thomson/South-Western
Slide 8
Example: Slater's Buffet
Expected Value of x E(x) = (a + b)/2 = (5 + 15)/2 = 10 Variance of x Var(x) = (b - a)2/12 = (15 5)2/12 = 8.33
2003 Thomson/South-Western
Slide 9
Normal Probability Distribution
The normal probability distribution is the most important distribution for describing a continuous random variable. It has been used in a wide variety of applications: Heights and weights of people Test scores Scientific measurements Amounts of rainfall It is widely used in statistical inference
2003 Thomson/South-Western
Slide 10
Normal Probability Distribution
Normal Probability Density Function
1 ( x )2 / 2 2 f ( x) e 2
where:
= mean = standard deviation = 3.14159
e = 2.71828
2003 Thomson/South-Western
Slide 11
Normal Probability Distribution
Graph of the Normal Probability Density Function f(x)
2003 Thomson/South-Western
Slide 12
Normal Probability Distribution
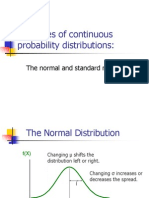
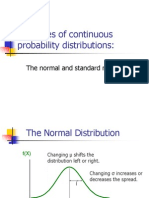
Characteristics of the Normal Probability Distribution The distribution is symmetric, and is often illustrated as a bell-shaped curve. Two parameters, (mean) and (standard deviation), determine the location and shape of the distribution. The highest point on the normal curve is at the mean, which is also the median and mode. The mean can be any numerical value: negative, zero, or positive. continued
Slide 13
2003 Thomson/South-Western
Normal Probability Distribution
Characteristics of the Normal Probability Distribution The standard deviation determines the width of the curve: larger values result in wider, flatter curves. = 10
= 50
2003 Thomson/South-Western
Slide 14
Normal Probability Distribution
Characteristics of the Normal Probability Distribution The total area under the curve is 1 (.5 to the left of the mean and .5 to the right). Probabilities for the normal random variable are given by areas under the curve.
2003 Thomson/South-Western
Slide 15
Normal Probability Distribution
Characteristics of the Normal Probability Distribution 68.26% of values of a normal random variable are within +/- 1 standard deviation of its mean. 95.44% of values of a normal random variable are within +/- 2 standard deviations of its mean. 99.72% of values of a normal random variable are within +/- 3 standard deviations of its mean.
2003 Thomson/South-Western
Slide 16
Standard Normal Probability Distribution
A random variable that has a normal distribution with a mean of zero and a standard deviation of one is said to have a standard normal probability distribution. The letter z is commonly used to designate this normal random variable. Converting to the Standard Normal Distribution
We can think of z as a measure of the number of standard deviations x is from .
Slide 17
2003 Thomson/South-Western
Example: Pep Zone
Standard Normal Probability Distribution Pep Zone sells auto parts and supplies including a popular multi-grade motor oil. When the stock of this oil drops to 20 gallons, a replenishment order is placed. The store manager is concerned that sales are being lost due to stockouts while waiting for an order. It has been determined that leadtime demand is normally distributed with a mean of 15 gallons and a standard deviation of 6 gallons. The manager would like to know the probability of a stockout, P(x > 20).
2003 Thomson/South-Western Slide 18
Example: Pep Zone
Standard Normal Probability Distribution The Standard Normal table shows an area of .2967 for the region between the z = 0 and z = .83 lines below. The shaded tail area is .5 - .2967 = .2033. The probability of a stockout is .2033. z = (x - )/ = (20 - 15)/6 = .83 Area = .2967 Area = .5 - .2967 = .2033 Area = .5 0 .83 z
Slide 19
2003 Thomson/South-Western
Example: Pep Zone
Using the Standard Normal Probability Table
.00 .01 .02 .03 .04 .05 .06 .07 .08 .09
.0 .0000 .0040 .0080 .0120 .0160 .0199 .0239 .0279 .0319 .0359 .1 .0398 .0438 .0478 .0517 .0557 .0596 .0636 .0675 .0714 .0753 .2 .0793 .0832 .0871 .0910 .0948 .0987 .1026 .1064 .1103 .1141 .3 .1179 .1217 .1255 .1293 .1331 .1368 .1406 .1443 .1480 .1517 .4 .5 .6 .7 .8 .9 .1554 .1591 .1628 .1664 .1700 .1736 .1772 .1808 .1844 .1879 .1915 .1950 .1985 .2019 .2054 .2088 .2123 .2157 .2190 .2224 .2257 .2291 .2324 .2357 .2389 .2422 .2454 .2486 .2518 .2549 .2580 .2612 .2642 .2673 .2704 .2734 .2764 .2794 .2823 .2852 .2881 .2910 .2939 .2967 .2995 .3023 .3051 .3078 .3106 .3133 .3159 .3186 .3212 .3238 .3264 .3289 .3315 .3340 .3365 .3389
Slide 20
2003 Thomson/South-Western
Example: Pep Zone
Standard Normal Probability Distribution If the manager of Pep Zone wants the probability of a stockout to be no more than .05, what should the reorder point be?
Area = .05 Area = .5 Area = .45 z.05 0 Let z.05 represent the z value cutting the .05 tail area.
2003 Thomson/South-Western Slide 21
Example: Pep Zone
Using the Standard Normal Probability Table We now look-up the .4500 area in the Standard Normal Probability table to find the corresponding z.05 value.
z . .00 . .01 . .02 . .03 . .04 . .05 . .06 . .07 . .08 . .09 .
1.5 .4332 .4345 .4357 .4370 .4382 .4394 .4406 .4418 .4429 .4441 1.6 .4452 .4463 .4474 .4484 .4495 .4505 .4515 .4525 .4535 .4545 1.7 .4554 .4564 .4573 .4582 .4591 .4599 .4608 .4616 .4625 .4633 1.8 .4641 .4649 .4656 .4664 .4671 .4678 .4686 .4693 .4699 .4706 1.9 .4713 .4719 .4726 .4732 .4738 .4744 .4750 .4756 .4761 .4767 . . . . . . . . . . .
z.05 = 1.645 is a reasonable estimate.
2003 Thomson/South-Western Slide 22
Example: Pep Zone
Standard Normal Probability Distribution The corresponding value of x is given by x = + z.05 = 15 + 1.645(6) = 24.87 A reorder point of 24.87 gallons will place the probability of a stockout during leadtime at .05. Perhaps Pep Zone should set the reorder point at 25 gallons to keep the probability under .05.
2003 Thomson/South-Western
Slide 23
Exponential Probability Distribution
The exponential probability distribution is useful in describing the time it takes to complete a task. The exponential random variables can be used to describe: Time between vehicle arrivals at a toll booth Time required to complete a questionnaire Distance between major defects in a highway
2003 Thomson/South-Western
Slide 24
Exponential Probability Distribution
Exponential Probability Density Function
f ( x)
e x / for x > 0, > 0
where:
= mean
e = 2.71828
2003 Thomson/South-Western
Slide 25
Exponential Probability Distribution
Cumulative Exponential Distribution Function
P ( x x0 ) 1 e xo /
where: x0 = some specific value of x
2003 Thomson/South-Western
Slide 26
Example: Als Carwash
Exponential Probability Distribution The time between arrivals of cars at Als Carwash follows an exponential probability distribution with a mean time between arrivals of 3 minutes. Al would like to know the probability that the time between two successive arrivals will be 2 minutes or less. P(x < 2) = 1 - 2.71828-2/3 = 1 - .5134 = .4866
2003 Thomson/South-Western
Slide 27
Example: Als Carwash
Graph of the Probability Density Function
f(x) .4
.3 .2 P(x < 2) = area = .4866
.1
x 1 2 3 4 5 6 7 8 9 10
Time Between Successive Arrivals (mins.)
2003 Thomson/South-Western
Slide 28
Relationship between the Poisson and Exponential Distributions
(If) the Poisson distribution provides an appropriate description of the number of occurrences per interval
(If) the exponential distribution provides an appropriate description of the length of the interval between occurrences
2003 Thomson/South-Western Slide 29
End of Chapter 6
2003 Thomson/South-Western
Slide 30
You might also like
- CHAPTER3 Continuous Probability DistributionDocument56 pagesCHAPTER3 Continuous Probability DistributionMari Parian ÜNo ratings yet
- Statistics For Business and Economics: Bab 6Document26 pagesStatistics For Business and Economics: Bab 6baloNo ratings yet
- Uniform Probability Distribution Normal Probability Distribution Exponential Probability DistributionDocument29 pagesUniform Probability Distribution Normal Probability Distribution Exponential Probability DistributionHuseynov AliNo ratings yet
- Continuous Probability DistributionsDocument48 pagesContinuous Probability DistributionsDaniel Tri RamadhaniNo ratings yet
- Week 4 UNIT IDocument25 pagesWeek 4 UNIT IJatin MehraNo ratings yet
- Slides Prepared by John S. Loucks St. Edward's University: 1 Slide © 2003 Thomson/South-WesternDocument34 pagesSlides Prepared by John S. Loucks St. Edward's University: 1 Slide © 2003 Thomson/South-WesternHRish BhimberNo ratings yet
- Normal DistributionDocument38 pagesNormal DistributionkenechidukorNo ratings yet
- Ch06.continous Probability DistributionsDocument26 pagesCh06.continous Probability DistributionsGladys Oryz BerlianNo ratings yet
- Probability and Statistics Mat 271EDocument50 pagesProbability and Statistics Mat 271Egio100% (1)
- Normal Probability DistributionsDocument8 pagesNormal Probability DistributionsCharmaine Reyes FabellaNo ratings yet
- Topic 2 Part III PDFDocument30 pagesTopic 2 Part III PDFChris MastersNo ratings yet
- Session 13 &14 Continuous Probability DistributionDocument50 pagesSession 13 &14 Continuous Probability DistributionRajneesh SarojNo ratings yet
- Normal Distribution and Probability: Mate14 - Design and Analysis of Experiments in Materials EngineeringDocument23 pagesNormal Distribution and Probability: Mate14 - Design and Analysis of Experiments in Materials EngineeringsajeerNo ratings yet
- 5 Normal DistributionDocument34 pages5 Normal DistributionLa JeNo ratings yet
- Slides Prepared by John S. Loucks St. Edward's University: 1 Slide © 2003 Thomson/South-WesternDocument36 pagesSlides Prepared by John S. Loucks St. Edward's University: 1 Slide © 2003 Thomson/South-WesternHRish BhimberNo ratings yet
- CH 6 Continuous Probability Distributions: 6.1 Uniform Distribution 6.2 Normal DistributionDocument38 pagesCH 6 Continuous Probability Distributions: 6.1 Uniform Distribution 6.2 Normal Distributionkaran79No ratings yet
- Decision Making in Operations ManagementDocument52 pagesDecision Making in Operations ManagementTin Keiiy0% (1)
- Properties of A Normal DistributionDocument8 pagesProperties of A Normal DistributionCarmelle BahadeNo ratings yet
- Slides Prepared by John S. Loucks St. Edward's University: 1 Slide © 2003 Thomson/South-WesternDocument54 pagesSlides Prepared by John S. Loucks St. Edward's University: 1 Slide © 2003 Thomson/South-WesternHRish BhimberNo ratings yet
- CHAPTER 1 Part 2 StudentDocument4 pagesCHAPTER 1 Part 2 StudentNasuha MutalibNo ratings yet
- Normal Distribn TheoryDocument16 pagesNormal Distribn TheoryGuru Ballur0% (1)
- Chapter2-New (Compatibility Mode)Document52 pagesChapter2-New (Compatibility Mode)Hafiz SuhaimiNo ratings yet
- Chapter 3 Part B: Probability DistributionDocument42 pagesChapter 3 Part B: Probability Distributionalexbell2k12No ratings yet
- CH7 - Continuous Probability DistributionDocument50 pagesCH7 - Continuous Probability Distributionlaelafitrya0% (1)
- Probility DistributionDocument41 pagesProbility Distributionnitindhiman30No ratings yet
- 4.3 Normal Probability Distributions: The Most Important Probability Distribution in StatisticsDocument37 pages4.3 Normal Probability Distributions: The Most Important Probability Distribution in StatisticsNelson ChambiNo ratings yet
- John S. Loucks: Slides Prepared byDocument58 pagesJohn S. Loucks: Slides Prepared bythemoonzoneNo ratings yet
- Chapter 5Document104 pagesChapter 5July ZergNo ratings yet
- Chapter 5Document23 pagesChapter 5Doug BezerediNo ratings yet
- Normal Distribution StanfordDocument43 pagesNormal Distribution Stanfordapi-204699162100% (1)
- Statistics - Discrete Probability DistributionsDocument36 pagesStatistics - Discrete Probability DistributionsDr Rushen SinghNo ratings yet
- Normal Distribution CollectionDocument40 pagesNormal Distribution CollectionVivek ParulekarNo ratings yet
- Freq Dist S 13 SlidesDocument112 pagesFreq Dist S 13 SlidestranthevutNo ratings yet
- Examples of Continuous Probability Distributions:: The Normal and Standard NormalDocument57 pagesExamples of Continuous Probability Distributions:: The Normal and Standard NormalPawan JajuNo ratings yet
- Slides Prepared by John S. Loucks St. Edward's University: 1 Slide © 2003 Thomson/South-WesternDocument34 pagesSlides Prepared by John S. Loucks St. Edward's University: 1 Slide © 2003 Thomson/South-WesternHRish BhimberNo ratings yet
- Newton-Raphson MethodDocument32 pagesNewton-Raphson MethodDave ImpresoNo ratings yet
- The Newton Raphson MethodDocument39 pagesThe Newton Raphson MethodElisa LaseNo ratings yet
- Ken Black QA ch06Document37 pagesKen Black QA ch06Rushabh VoraNo ratings yet
- Essentials of Modern Business StatisticsDocument32 pagesEssentials of Modern Business StatisticsWaqar ZulfiqarNo ratings yet
- Introduction To Continuous Probability Distributions: Prepared By: Renna MagdalenaDocument46 pagesIntroduction To Continuous Probability Distributions: Prepared By: Renna Magdalenarenna_magdalenaNo ratings yet
- 39 2 Norm Approx Bin PDFDocument8 pages39 2 Norm Approx Bin PDFsound05No ratings yet
- Ch3c Random Variables ContinuousDocument80 pagesCh3c Random Variables Continuouskhawla2789No ratings yet
- The Normal Distribution 5: Elementary StatisticsDocument34 pagesThe Normal Distribution 5: Elementary StatisticsNoor HafizahNo ratings yet
- CH 02Document53 pagesCH 02K60 Ngô Thị Cẩm NhungNo ratings yet
- Chapter6 IPS14eDocument23 pagesChapter6 IPS14eSamantha Cruz BlancoNo ratings yet
- Q3 Module 3 - by PairDocument12 pagesQ3 Module 3 - by Pairdwyanesisneros19No ratings yet
- Chapter 6 Continuous Probability DistributionsDocument10 pagesChapter 6 Continuous Probability DistributionsAnastasiaNo ratings yet
- P1.T2. Quantitative Analysis Bionic Turtle FRM Practice Questions Reading 13Document12 pagesP1.T2. Quantitative Analysis Bionic Turtle FRM Practice Questions Reading 13Ravi Chandra0% (1)
- 2 Random Variables and Probability DistributionsDocument36 pages2 Random Variables and Probability Distributionsminh tranNo ratings yet
- Sampling Distributions LectureDocument51 pagesSampling Distributions LectureajayNo ratings yet
- Examples of Continuous Probability Distributions:: The Normal and Standard NormalDocument57 pagesExamples of Continuous Probability Distributions:: The Normal and Standard NormalAkshay VetalNo ratings yet
- QTM Cycle 7 Session 4Document79 pagesQTM Cycle 7 Session 4OttilieNo ratings yet
- Stat Chapter 6 BDocument25 pagesStat Chapter 6 BMohamed Abd El-MoniemNo ratings yet
- Sampling Distribution WebDocument11 pagesSampling Distribution WebAbdul QadeerNo ratings yet
- 37 2Document20 pages37 2Mayar ZoNo ratings yet
- Tutorial Questions 1 SolutionsDocument5 pagesTutorial Questions 1 SolutionsayariseifallahNo ratings yet
- Rcom Abridged 2012-13Document96 pagesRcom Abridged 2012-13Jason RobertsonNo ratings yet
- India's Telecommunication Network Is The Second Largest in TheDocument7 pagesIndia's Telecommunication Network Is The Second Largest in TheHRish BhimberNo ratings yet
- 13525module 1Document252 pages13525module 1DrVikram NaiduNo ratings yet
- Summer InternshipDocument5 pagesSummer InternshipHRish BhimberNo ratings yet
- Specific OrderDocument12 pagesSpecific OrderHRish BhimberNo ratings yet
- Detailed Cost StructureDocument7 pagesDetailed Cost StructureHRish BhimberNo ratings yet
- Credit RatingDocument18 pagesCredit RatingAmanjyot SinghNo ratings yet
- At05 Pp01 Conventional SignsDocument18 pagesAt05 Pp01 Conventional SignsHRish BhimberNo ratings yet
- EntrepreneurshipDocument75 pagesEntrepreneurshipHRish BhimberNo ratings yet
- MDocument4 pagesMHRish BhimberNo ratings yet
- Conventional Signs: and Further Information To The Swiss Topographic MapsDocument7 pagesConventional Signs: and Further Information To The Swiss Topographic MapsHRish BhimberNo ratings yet
- LeasingDocument9 pagesLeasingHRish BhimberNo ratings yet
- Capital Budgeting MethodsDocument17 pagesCapital Budgeting MethodsHRish BhimberNo ratings yet
- Explain The Importance of Purchasing in A Manufacturing OrganizationDocument14 pagesExplain The Importance of Purchasing in A Manufacturing OrganizationHRish BhimberNo ratings yet
- Slides Prepared by John S. Loucks St. Edward's University: 1 Slide © 2003 Thomson/South-WesternDocument51 pagesSlides Prepared by John S. Loucks St. Edward's University: 1 Slide © 2003 Thomson/South-WesternHRish BhimberNo ratings yet
- Case Study 4 February 2000-Narmada ProjectDocument14 pagesCase Study 4 February 2000-Narmada ProjectHRish BhimberNo ratings yet
- Slides Prepared by John S. Loucks St. Edward's University: 1 Slide © 2003 Thomson/South-WesternDocument44 pagesSlides Prepared by John S. Loucks St. Edward's University: 1 Slide © 2003 Thomson/South-WesternHRish BhimberNo ratings yet
- Slides Prepared by John S. Loucks St. Edward's University: 1 Slide © 2003 Thomson/South-WesternDocument36 pagesSlides Prepared by John S. Loucks St. Edward's University: 1 Slide © 2003 Thomson/South-WesternHRish BhimberNo ratings yet
- Slides Prepared by John S. Loucks St. Edward's University: 1 Slide © 2003 Thomson/South-WesternDocument54 pagesSlides Prepared by John S. Loucks St. Edward's University: 1 Slide © 2003 Thomson/South-WesternHRish BhimberNo ratings yet
- Capital Budgeting MethodsDocument17 pagesCapital Budgeting MethodsHRish BhimberNo ratings yet
- Slides Prepared by John S. Loucks St. Edward's University: 1 Slide © 2003 Thomson/South-WesternDocument54 pagesSlides Prepared by John S. Loucks St. Edward's University: 1 Slide © 2003 Thomson/South-WesternHRish BhimberNo ratings yet
- Slides Prepared by John S. Loucks St. Edward's University: 1 Slide © 2003 Thomson/South-WesternDocument34 pagesSlides Prepared by John S. Loucks St. Edward's University: 1 Slide © 2003 Thomson/South-WesternHRish BhimberNo ratings yet
- Slides Prepared by John S. Loucks St. Edward's University: 1 Slide © 2003 Thomson/South-WesternDocument34 pagesSlides Prepared by John S. Loucks St. Edward's University: 1 Slide © 2003 Thomson/South-WesternHRish BhimberNo ratings yet
- Slides Prepared by John S. Loucks St. Edward's University: 1 Slide © 2003 Thomson/South-WesternDocument28 pagesSlides Prepared by John S. Loucks St. Edward's University: 1 Slide © 2003 Thomson/South-WesternHRish BhimberNo ratings yet
- Accounting StandardDocument6 pagesAccounting StandardHRish BhimberNo ratings yet
- Overview of An Organization Chart in PowerpointDocument3 pagesOverview of An Organization Chart in PowerpointHRish BhimberNo ratings yet
- Statistics Full BookDocument135 pagesStatistics Full BookHRish BhimberNo ratings yet
- Slides Prepared by John S. Loucks St. Edward's University: 1 Slide © 2003 Thomson/South-WesternDocument34 pagesSlides Prepared by John S. Loucks St. Edward's University: 1 Slide © 2003 Thomson/South-WesternHRish BhimberNo ratings yet
- LeasingDocument9 pagesLeasingHRish BhimberNo ratings yet
- Market AnomaliesDocument8 pagesMarket AnomaliesUsman KashifNo ratings yet
- Dependent T TestDocument38 pagesDependent T TestRatna Monika SariNo ratings yet
- Stat Quiz BallDocument85 pagesStat Quiz BallMa. Jessa Dane NgohoNo ratings yet
- Assignment 1 AnswersDocument5 pagesAssignment 1 AnswerspellaraNo ratings yet
- Standard Costing Variance AnalysisDocument4 pagesStandard Costing Variance AnalysisAntonette Eve CelomineNo ratings yet
- Q3 Module 18 CLMD4ASTAT&PROB 225-237Document13 pagesQ3 Module 18 CLMD4ASTAT&PROB 225-237KyotieNo ratings yet
- Student's T TestDocument56 pagesStudent's T TestmelprvnNo ratings yet
- Co1 StatDocument25 pagesCo1 StatEleonor SandinoNo ratings yet
- MSQ 03 Standard Costs and Variance Analysis BrylDocument13 pagesMSQ 03 Standard Costs and Variance Analysis BrylDavid DavidNo ratings yet
- 3 Materials Mix and Yield Variances F5 ACCA Technical Article PDFDocument5 pages3 Materials Mix and Yield Variances F5 ACCA Technical Article PDFSamuel AbebawNo ratings yet
- SPSS Activity 3Document8 pagesSPSS Activity 3Carmel YparraguirreNo ratings yet
- 4SSMN902 May 2022Document10 pages4SSMN902 May 2022MattNo ratings yet
- Distance MBA Master of Business Administrator Syllabus by KSOUDocument11 pagesDistance MBA Master of Business Administrator Syllabus by KSOUSunil JhaNo ratings yet
- The Value Premium FFDocument20 pagesThe Value Premium FFbeatrizvasconcelos.2001No ratings yet
- BORRADAILE 2003 - Statistics of Earth Science Data LB 6029 PDFDocument371 pagesBORRADAILE 2003 - Statistics of Earth Science Data LB 6029 PDFEduardo100% (1)
- Research Answers 1Document42 pagesResearch Answers 1Mig TigNo ratings yet
- Calvo, Ernesto. The Eye of The BeholderDocument25 pagesCalvo, Ernesto. The Eye of The Beholderaguirregermanr_53039No ratings yet
- Advanced Topics in Introductory ProbabilityDocument275 pagesAdvanced Topics in Introductory ProbabilityMusfirah AamirNo ratings yet
- Rice Lake IQ6200 6500Document41 pagesRice Lake IQ6200 6500Ana Gabriela OjedaNo ratings yet
- Psych Math NotesDocument3 pagesPsych Math NotesHannah MondillaNo ratings yet
- Cornerstones of Cost Management Ch09Document45 pagesCornerstones of Cost Management Ch09Bobby Patel0% (1)
- Test Bank For Basic Statistics For The Behavioral Sciences 7th EditionDocument24 pagesTest Bank For Basic Statistics For The Behavioral Sciences 7th EditionNicoleJohnsongobe100% (46)
- ExpandedDocument3 pagesExpandedno oneNo ratings yet
- Binomialnegativaheterogenea PDFDocument6 pagesBinomialnegativaheterogenea PDFRamonfebreroNo ratings yet
- Answer All The QuestionsDocument5 pagesAnswer All The QuestionsSayapPutihNo ratings yet
- Employee AbsenteeismDocument88 pagesEmployee AbsenteeismRajesh Khatkar100% (4)
- Leary 2001 Introduction To Behavioral Research Methods - Cap 8 - 9Document59 pagesLeary 2001 Introduction To Behavioral Research Methods - Cap 8 - 9raverokkNo ratings yet
- Black LittermanDocument51 pagesBlack LittermanHeshmat SeyyediNo ratings yet