Professional Documents
Culture Documents
New Quantum Lower Bound Method, With Applications To Direct Product Theorems
Uploaded by
gabrieldevotoOriginal Description:
Original Title
Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
New Quantum Lower Bound Method, With Applications To Direct Product Theorems
Uploaded by
gabrieldevotoCopyright:
Available Formats
New quantum lower bound
method, with applications to
direct product theorems
Andris Ambainis, U. Waterloo
Robert Spalek, CWI, Amsterdam
Ronald de Wolf, CWI, Amsterdam
Query model
Input x
1
, , x
N
accessed by queries.
Complexity = the number of queries.
0 1 0 0
...
x
1
x
2
x
N
x
3
i
0
i
x
i
Grover's search
Is there i such that x
i
=1?
Queries: ask i, get x
i
.
Classically, N queries required.
Quantum: O(\N) queries [Grover, 1996].
Speeds up any search problem.
0 1 0 0
...
x
1
x
2
x
N
x
3
Quantum counting [Boyer et
al., 1998]
Is the fraction of i:x
i
=1 more than +c or
less than -c ?
Classical: queries.
Quantum: queries.
0 1 0 0
...
x
1
x
2
x
N
x
3
|
.
|
\
|
O
2
1
c
|
.
|
\
|
c
1
O
Element distinctness
Are there i, j such that i=j but x
i
=x
j
?
Classically: N queries.
Quantum: O(N
2/3
).
3 1 17 5
...
x
1
x
2
x
N
x
3
Lower bounds
Search requires O(\N) queries [Bennett
et al., 1997].
Counting: O(1/c) [Nayak, Wu, 1999].
Element distinctness: O (N
2/3
) [Shi,
2002].
Lower bound methods
Adversary: analyze algorithm, prove it is
incorrect on some input.
Polynomials: describe algorithm by low
degree polynomial.
Which method?
Problem Adversary Polynomials
Search Yes Yes
Counting Yes Yes
Element dist. ? Yes
Limits of adversary method
Certificate for f on input (x
1
, x
2
, , x
N
):
set of variables x
i
which determine
f(x
1
, x
2
, , x
N
).
Search: is there i:x
i
=1?
0 1 0 0
...
x
1
x
2
x
N
x
3
Limits of adversary method
Certificate for f on input (x
1
, x
2
, , x
N
):
set of variables x
i
which determine
f(x
1
, x
2
, , x
N
).
Search: is there i:x
i
=1?
0 0 0 0
...
x
1
x
2
x
N
x
3
Certificate complexity
C
x
(f): the size of the smallest certificate
for f on the input x.
) ( max ) (
0 ) ( : 0
f C f C
x x f x =
=
) ( max ) (
1 ) ( : 1
f C f C
x x f x =
=
Search: C
0
=N, C
1
=1.
Limits of adversary method
Theorem [Spalek, Szegedy, 2004]
Any quantum adversary lower bound is
at most
( ) N f C f C O - )) ( ), ( min(
1 0
Example:element distinctness
Are there i, j:x
i
= x
j
?
1-certificate: {i, j}, x
i
= x
j.
Adversary bound:
Actual complexity: O(N
2/3
).
( ) ( ) N O N O = - 2
3 1 17 5
...
x
1
x
2
x
N
x
3
Example: triangle finding
Graph G, specified by N
2
variables x
ij
:
x
ij
=1, if there is edge between i and j.
Does G contain a triangle?
1-certificate:{ij, jk, ik}, x
ij
= x
ik
= x
jk
=1.
Adversary lower bound: at most
The best algorithm: O(N
1.3
) [MSS 03].
( ) ( ) N O N O = -
2
3
Previous adversary method
Quantum query model
Fixed starting state.
U
0
, U
1
, , U
T
independent of x
1
, x
2
,
, x
N
.
Q queries.
Measuring final state gives the result.
U
0
Q Q
start
U
1
U
T
Queries
Basis states for algorithms workspace:
|i, z), ie{1, 2, , N}.
Query transformation:
Example:
|i, z)|i, z), if x
i
=0;
|i, z)-|i, z), if x
i
=1;
z Q i z i Q
i
x
= ,
| )
Adversary framework
Quantum
algorithm A
x
1
x
2
x
N
N x x N
x x x Q x x x
N
... ...
2 1 ... 2 1
1
Two registers: H
A
, H
I
.
Query Q:
Example:Grover search
Start state: |
start
)|
0
),
End state
( ) 1 ... 00 ... 0 ... 01 0 ... 10
1
0
+ + + =
N
( ) 1 ... 00 ... 0 ... 01 2 0 ... 10 1
1
N
N
+ + +
Density matrices
Measure H
A
, look at density matrix of H
I
|
|
|
|
|
|
|
.
|
\
|
=
N
N
N
end
1
0 0
0
1
0
0 0
1
o
|
|
|
|
|
|
|
.
|
\
|
=
N N N
N N N
N N N
start
1 1 1
1 1 1
1 1 1
o
Density matrices
Sum of off-diagonal entries.
N(N-1) entries.
Sum for starting state:
Sum for end state: 0.
Query changes the sym by at most 2\N.
O(\N) queries needed.
1
1
) 1 ( = N
N
N N
Limits of this approach
(o
end
)
x, y
measures the possibility of
distinguishing x from y.
If every (o
end
)
x, y
small, we can, given x,
y: f(x) =f(y), distinguish x from y.
Limits of this approach
It might be that:
Every x can be
distinguished from
every y;
There is no
measurement that
distinguishes all x from
all y.
f(x)=0 f(y)=1
Adversary method fails
quantum algorithm
New method
K-fold search
K items i:x
i
=1, find all of them.
O(\NK) queries: O(\N/K) for each item.
This is optimal.
0 1 0 0
...
x
1
x
2
x
N
x
3
Direct product theorem
Theorem [KSW 04] Solving K-fold
search with success probability c
-K
, c>1
requires c\NK queries.
Easy to prove for success probability c.
Difficult for probability c
-K
.
Why is this useful????
Application:sorting
Theorem [KSW04] A quantum algorithm
for sorting x
1
, x
2
, , x
N
with S qubits of
workspace must use
queries.
|
|
.
|
\
|
O
S
N
5 . 1
Proof
Divide algorithm into stages: first K
items sorted, next K items sorted,
Suffices to show each stage requires
O(\NK) queries.
Each stage reduces to K-fold search.
Proof
At the beginning of i
th
stage, we get S
qubits from the previous stage.
Theorem K-fold search requires O(\NK)
queries, even if we allow K/C qubits of
advice.
Proof
Theorem K-fold search requires O(\NK)
queries, even if we allow K/C qubits of
advice.
Proof Replace advice by completely
mixed state.
Success probability p with advice =>
Success probability p2
-K/C
, no advice.
Direct product theorem
Theorem Solving K-fold search with
success probability c
-K
, c>1 requires
c\NK queries.
[KSW 04]: proof by polynomials
method.
This talk: (new) adversary method.
Proof sketch
Know-0, Know-1, , Know-k
states.
Describe quantum state as
=
K
j
j
j Know p
0
" "
| )
Proof
Adversary framework
Start state for input:
= = K x i
N
i
x x x
| } 1 : { |
2 1
Quantum
algorithm A
x
1
x
2
x
N
Proof
State of H
I
if we know
Subspace T
j
spanned by all
= = =
= =
=
1 ...
| } 1 : { |
2 1 ...
1
1
j
i i
i
j
x x
K x i
N i i
x x x
1 ...
1
= = =
j
i i
x x
j
i i ...
1
Proof
T
0
_T
1
_ _ T
K
.
T
0
starting state.
T
K
entire H
I
.
T
0
T
1
. T
K
T
j
know at-most j subspace
Proof
S
j
=T
j
(T
j-1
)
.
T
0
T
1
T
K
Proof
S
j
=T
j
(T
j-1
)
.
T
0
S
1
S
K
S
j
is know-j subspace.
Proof
|+) - state of algorithm including the
input register |x
1
x
N
).
|+
j
) belongs to H
A
S
j
.
Probability of know-j:
,
0
=
+ = +
K
j
j
2
j j
p + =
Proof
Start state: p
0
=1, p
1
==p
K
=0.
Change in one query:
After c\NK queries, p
K/2+1
, , p
K
are
exponentially small.
Success probability exponentially small.
( )
1 1 1
'
+ + +
+ + s
j j j j
p p
N
K
c p p
Threshold functions
F(x
1
, x
2
, , x
N
)=1 if x
i
=1 for at least t
values ie{1, 2, , N}.
F(x
1
, x
2
, , x
N
)=0 if x
i
=1 for at most t-1
values ie{1, 2, , N}.
Query complexity: O(\Nt).
0 1 0 0
...
x
1
x
2
x
N
x
3
Threshold functions
F(x
1
, x
2
, , x
N
)=1 if x
i
=1 for at least t
values ie{1, 2, , N}.
F(x
1
, x
2
, , x
N
)=0 if x
i
=1 for at most t-1
values ie{1, 2, , N}.
Query complexity: O(\Nt).
0 1 0 0
...
x
1
x
2
x
N
x
3
Threshold functions
K instances of threshold function.
O(K\Nt) queries.
Theorem Solving all K instances with
probability at most c
-K
requires cK\Nt
queries.
Proof
K input registers.
Each input register initially ,
|
0
), |
1
) - uniform over |x
1
x
N
) with
t-1 and t values i:x
i
=1.
1 0
+
Algorithm
1 1
2
1
1 N
x x x
K
N
K K
x x x
2 1
Proof
For each instance, states solved,
know-0, know-1, know-(t-1).
For K instances, vector of K states.
Progress of a state:
solved progress t/2.
know-t/2, know-(t-1) progress t/2.
know-j, j<t/2 progress j.
Proof
If progress of final state less than tK/4, the
probability of getting all K correct answers is
c
-K
.
Decompose current state
Potential function
=
j
j
j progress p " " o
( ) ,
=
j
j
j
q p P o
tN
q
1
1+ =
Proof
Start state: P(o)=1.
For p
j
, j>tK/4 to be more than c
-K
,
One query increases P(o) by at most a
factor of
( )
=
j
j
j
q p P o
( )
K tK K
C q c P > >
4 /
o
|
.
|
\
|
+
tN
O
1
1
Proof
F(x
1
, x
2
, , x
N
)=0, know-j:
F(x
1
, x
2
, , x
N
)=1, know-j:
= = =
= =
=
1 ...
1 | } 1 : { |
2 1
0
1
. . .
1
j
i i
i
j
i i
x x
t x i
N
x x x
= = =
= =
=
1 ...
| } 1 : { |
2 1
1
1
. . .
1
j
i i
i
j
i i
x x
t x i
N
x x x
Proof
Starting state:
Solved:
Know-j
1 0
+
1 0
. . .
1
. . .
1 j
i i
j
i i
1 0
. . .
1
. . .
1 j
i i
j
i i
+
Application: testing linear
inequalities
a
ij
known, x
i
, b
j
accessed by queries.
Which inequalities are true?
> + + +
> + + +
N N NN N N
N N
b x a x a x a
b x a x a x a
2 2 1 1
1 1 2 12 1 11
Our result
Memory limited to S (qu)bits.
Classically: O(N
2
/S) queries.
Quantum: O(N
3/2
t
1/2
/S
1/2
) queries.
Lower bound follows from threshold function
lower bound.
> + + +
> + + +
N N NN N N
N N
b x a x a x a
b x a x a x a
2 2 1 1
1 1 2 12 1 11
Conclusion
New quantum lower bound method, by
eigenspace analysis.
Direct product theorems for K-fold
search and threshold functions.
Consequences for time-space tradeoffs.
More details
A. Ambainis. A new quantum lower
bound method, with application to
direct product theorem for search,
quant-ph/0508200.
A. Ambainis, R. Spalek, R. de Wolf,
Quantum direct product theorems for
symmetric functions and time-space
tradeoffs , quant-ph/0511200.
Open problems
AND-OR tree: best
lower bound O(\N),
N number of
variables.
Algorithm: O(N
.753
).
x
1
x
2
x
3
x
4
AND
OR OR
Adversary lower
bound for element
distinctness?
You might also like
- Multiple-Choice Questions: 1 A B C D EDocument6 pagesMultiple-Choice Questions: 1 A B C D EJohnNo ratings yet
- 04-Induction and RecursionDocument32 pages04-Induction and Recursionvietpvhe186335No ratings yet
- Induction and RecursionDocument34 pagesInduction and RecursionVĩ KhangNo ratings yet
- Induction and Recursion Quy nạp và Đệ quyDocument31 pagesInduction and Recursion Quy nạp và Đệ quyToan NgoNo ratings yet
- Introduction To Approximation Algorithms: Optimization Algorithms in Production ManagementDocument29 pagesIntroduction To Approximation Algorithms: Optimization Algorithms in Production Managementplasa88No ratings yet
- Algorithms AnalysisDocument25 pagesAlgorithms Analysislyhoangkhang831No ratings yet
- Applied Econometrics: Department of Economics Stern School of BusinessDocument27 pagesApplied Econometrics: Department of Economics Stern School of BusinesschatfieldlohrNo ratings yet
- Name: CS 495/MA 405: Analysis of Algorithms - Test 1 Problem 1-1: Answer: Problem 1-2: AnswerDocument6 pagesName: CS 495/MA 405: Analysis of Algorithms - Test 1 Problem 1-1: Answer: Problem 1-2: AnswerIvaj ZuckerbergNo ratings yet
- Successive Quadratic ProgrammingDocument33 pagesSuccessive Quadratic Programmingsathish22No ratings yet
- IMC 2010 (Day 2)Document4 pagesIMC 2010 (Day 2)Liu ShanlanNo ratings yet
- R x f ξ n+1 ! x−x: Taylorov red (Mac Laurinov red)Document13 pagesR x f ξ n+1 ! x−x: Taylorov red (Mac Laurinov red)Hinko FušNo ratings yet
- U 2Document20 pagesU 2ganeshrjNo ratings yet
- Advanced Algorithms Analysis and Design: by Dr. Nazir Ahmad ZafarDocument15 pagesAdvanced Algorithms Analysis and Design: by Dr. Nazir Ahmad Zafaraamir aliNo ratings yet
- Algorithms 1Document10 pagesAlgorithms 1reema alafifiNo ratings yet
- Tema5 Teoria-2830Document57 pagesTema5 Teoria-2830Luis Alejandro Sanchez SanchezNo ratings yet
- Number Theory Algorithms and Cryptography AlgorithmsDocument50 pagesNumber Theory Algorithms and Cryptography AlgorithmsimnomusNo ratings yet
- Spectral Expansion Solutions For Markov-Modulated Queues: Unbounded Queue in A Finite-State Markovian EnvironmentDocument19 pagesSpectral Expansion Solutions For Markov-Modulated Queues: Unbounded Queue in A Finite-State Markovian EnvironmentAbhilash SharmaNo ratings yet
- Quicksort: Quicksort (A, P, R) : Ifn 1:return Q Partition (A, P, R) Quicksort (A, P, q-1) Quicksort (A, q+1, R)Document6 pagesQuicksort: Quicksort (A, P, R) : Ifn 1:return Q Partition (A, P, R) Quicksort (A, P, q-1) Quicksort (A, q+1, R)Andrew LeeNo ratings yet
- Durbin LevinsonDocument7 pagesDurbin LevinsonNguyễn Thành AnNo ratings yet
- Strong Mathematical Induction: (Proving, Validation and Verification, ETC.)Document14 pagesStrong Mathematical Induction: (Proving, Validation and Verification, ETC.)feelNo ratings yet
- Design and Analysis of Algorithms Trial Exam: Ade Azurat - Fasilkom UI September 30, 2010Document13 pagesDesign and Analysis of Algorithms Trial Exam: Ade Azurat - Fasilkom UI September 30, 2010masChilmanNo ratings yet
- Weatherwax - Conte - Solution - Manual Capitulo 2 y 3Document59 pagesWeatherwax - Conte - Solution - Manual Capitulo 2 y 3Jorge EstebanNo ratings yet
- Experiment-5 Evaluating The Fourier Coefficients of Square WaveDocument25 pagesExperiment-5 Evaluating The Fourier Coefficients of Square WaveKartikNo ratings yet
- Dynamic ProgrammingDocument7 pagesDynamic ProgrammingGlenn GibbsNo ratings yet
- Final Exam - Question BookletDocument8 pagesFinal Exam - Question BookletShiva CharanNo ratings yet
- ProblemsDocument62 pagesProblemserad_5No ratings yet
- Lecture19 20 21Document14 pagesLecture19 20 21915431916No ratings yet
- Unit-1 DAA - NotesDocument25 pagesUnit-1 DAA - Notesshivam02774No ratings yet
- Mth1114 Induction Andrecursion MINEDocument30 pagesMth1114 Induction Andrecursion MINEgoo zong linNo ratings yet
- Factorization Reduced To Order FindingDocument4 pagesFactorization Reduced To Order FindingavnishNo ratings yet
- L5 Asmptotic NotationsDocument7 pagesL5 Asmptotic NotationsNama RahasiaNo ratings yet
- DAADocument62 pagesDAAanon_385854451No ratings yet
- Randomized Algorithms: Tutorial 3 Hints For Homework 2Document31 pagesRandomized Algorithms: Tutorial 3 Hints For Homework 2Shivprasad ShahapurkarNo ratings yet
- Sol 05Document8 pagesSol 05Minh TrươngNo ratings yet
- EE5130: Digital Signal ProcessingDocument3 pagesEE5130: Digital Signal ProcessingSHUBHAM ANAND VERMA EE20M540No ratings yet
- The Growth of Functions: Rosen 2.2Document36 pagesThe Growth of Functions: Rosen 2.2Luis LoredoNo ratings yet
- Lec7matrixnorm Part4Document13 pagesLec7matrixnorm Part4Somnath DasNo ratings yet
- Selecting The Right JobsDocument28 pagesSelecting The Right JobsIoannisNo ratings yet
- Tutorial: Quantum Algorithms: Julia KempeDocument16 pagesTutorial: Quantum Algorithms: Julia KempeSaif HassanNo ratings yet
- Atserias Oberwolfach2017Document103 pagesAtserias Oberwolfach2017Kevin MondragonNo ratings yet
- 3: Divide and Conquer: Fourier Transform: PolynomialDocument8 pages3: Divide and Conquer: Fourier Transform: PolynomialIrmak ErkolNo ratings yet
- 3: Divide and Conquer: Fourier Transform: PolynomialDocument8 pages3: Divide and Conquer: Fourier Transform: PolynomialCajun SefNo ratings yet
- 2016 - 2 - BlagoevgradDocument5 pages2016 - 2 - BlagoevgradCătălin BordeaNo ratings yet
- Module1 Lecture3Document18 pagesModule1 Lecture3Vivek GargNo ratings yet
- Solusi 4.18Document4 pagesSolusi 4.18MivTah Al BughisiyyahNo ratings yet
- Aaa 7Document36 pagesAaa 7Muhammad Khaleel AfzalNo ratings yet
- Unit 4Document28 pagesUnit 4Dr. Nageswara Rao EluriNo ratings yet
- Asymptotic Notation: Steven SkienaDocument17 pagesAsymptotic Notation: Steven SkienasatyabashaNo ratings yet
- Elec2600 Lecture Part III HDocument237 pagesElec2600 Lecture Part III HGhoshan JaganathamaniNo ratings yet
- 03-The Fundamentals - Algorithms - IntegersDocument54 pages03-The Fundamentals - Algorithms - Integerstungnt26999No ratings yet
- Midterm SolutionsDocument5 pagesMidterm SolutionsLinbailuBellaJiangNo ratings yet
- NP-hard Problems and Approximation Algorithms: 10.1 What Is The Class NP?Document29 pagesNP-hard Problems and Approximation Algorithms: 10.1 What Is The Class NP?Aleksandr TerranovaNo ratings yet
- Master's TheoremDocument13 pagesMaster's TheoremyashdhingraNo ratings yet
- Ahmadmj 3Document9 pagesAhmadmj 3Abdulhadi AhmadNo ratings yet
- Numerical Optimization: Unit 9: Penalty Method and Interior Point Method Unit 10: Filter Method and The Maratos EffectDocument24 pagesNumerical Optimization: Unit 9: Penalty Method and Interior Point Method Unit 10: Filter Method and The Maratos EffectkahvumidragaispeciNo ratings yet
- 8 QuickSortDocument29 pages8 QuickSortZeenat SiddiqNo ratings yet
- 2 Linear TransformationsDocument32 pages2 Linear TransformationsShanNo ratings yet
- CS174: Note12Document5 pagesCS174: Note12juggleninjaNo ratings yet
- Green's Function Estimates for Lattice Schrödinger Operators and Applications. (AM-158)From EverandGreen's Function Estimates for Lattice Schrödinger Operators and Applications. (AM-158)No ratings yet
- Jasper Reports Server CP Install GuideDocument82 pagesJasper Reports Server CP Install GuidegabrieldevotoNo ratings yet
- Matlab Ttutorial 2Document9 pagesMatlab Ttutorial 2Bizura SarumaNo ratings yet
- Covertura de BranchesDocument1 pageCovertura de BranchesgabrieldevotoNo ratings yet
- ConsultasDocument1 pageConsultasgabrieldevotoNo ratings yet
- PPSDocument94 pagesPPSaamirNo ratings yet
- (Boundary Elements 3) George T. Symm (auth.), Dr. Carlos A. Brebbia (eds.) - Boundary Element Methods_ Proceedings of the Third International Seminar, Irvine, California, July 1981-Springer-Verlag Ber.pdfDocument638 pages(Boundary Elements 3) George T. Symm (auth.), Dr. Carlos A. Brebbia (eds.) - Boundary Element Methods_ Proceedings of the Third International Seminar, Irvine, California, July 1981-Springer-Verlag Ber.pdfAnonymous hprsT3WlP100% (2)
- B.C.A. Semester - II BCA-203: Discrete Mathematics: Difference, D' Morgons Law, Subsets, Power Sets, Partitions SetsDocument2 pagesB.C.A. Semester - II BCA-203: Discrete Mathematics: Difference, D' Morgons Law, Subsets, Power Sets, Partitions SetsBenedictNo ratings yet
- Quantexpert Free Question Bank On EquationsDocument4 pagesQuantexpert Free Question Bank On EquationsutsavbathwalNo ratings yet
- Control Engineering Lec - 32Document25 pagesControl Engineering Lec - 32Sharath MunduriNo ratings yet
- Gauss Eliminasyon 4x4Document17 pagesGauss Eliminasyon 4x4Abdulvahap ÇakmakNo ratings yet
- Curve FittingDocument3 pagesCurve FittingDewaNo ratings yet
- 4 Trigonometric Transformation Trigonometric Substitution and RationalizingDocument10 pages4 Trigonometric Transformation Trigonometric Substitution and RationalizingTreesya EstradaNo ratings yet
- Timetable ILPDocument6 pagesTimetable ILPJimmy López PortilloNo ratings yet
- W3 Lesson 3 - Systems of Linear Equation - ModuleDocument11 pagesW3 Lesson 3 - Systems of Linear Equation - ModuleJitlee PapaNo ratings yet
- Gauss-Seidel Itration MethodDocument2 pagesGauss-Seidel Itration MethodNayli AthirahNo ratings yet
- Preboard MATH SetADocument10 pagesPreboard MATH SetAFritz FatigaNo ratings yet
- Stochastic Processes: 6.1 Poisson Process and Exponential Distribution 6.1.1 P P PDocument6 pagesStochastic Processes: 6.1 Poisson Process and Exponential Distribution 6.1.1 P P PGuilherme Vilas BoasNo ratings yet
- FM 3e SM Chap04Document77 pagesFM 3e SM Chap04SaAhRaNo ratings yet
- 1.3 Cycloid Vertical ConstructionDocument2 pages1.3 Cycloid Vertical ConstructionMartin De Boras PragashNo ratings yet
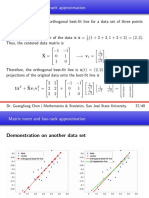
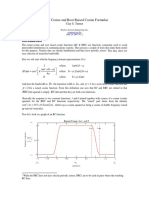
- Raised Cosine and Root Raised Cosine FormulaeDocument4 pagesRaised Cosine and Root Raised Cosine Formulaefaroo28No ratings yet
- B.Tech. Degree Examination Cse, Eee & It: (April-18) (EMA-208)Document2 pagesB.Tech. Degree Examination Cse, Eee & It: (April-18) (EMA-208)Dhanunjaya Reddy ManneNo ratings yet
- Ce304 - StabilityDocument2 pagesCe304 - StabilityTitin SundariNo ratings yet
- Linear Algebra Lecture NotesDocument50 pagesLinear Algebra Lecture NotesMichael SteeleNo ratings yet
- Pattern Recognition ExcerciseDocument30 pagesPattern Recognition ExcerciseMafrur RischanNo ratings yet
- Lecture 2: Roots of Equation: Dr. Nor Alafiza YunusDocument62 pagesLecture 2: Roots of Equation: Dr. Nor Alafiza YunusHaziq KhairiNo ratings yet
- Vector and Tensor Analysis 1950Document360 pagesVector and Tensor Analysis 1950Ray Minich89% (9)
- GurobiDocument16 pagesGurobiZewum KuNo ratings yet
- hw4 SolDocument5 pageshw4 SolrupadnNo ratings yet
- Probability and Statistics: Dr. K.W. Chow Mechanical EngineeringDocument113 pagesProbability and Statistics: Dr. K.W. Chow Mechanical EngineeringPriyaprasad PandaNo ratings yet
- 10CS661 Ia2 QBDocument3 pages10CS661 Ia2 QBpramelaNo ratings yet
- Chapter 3. Describing Data-Numerical MeasuresDocument24 pagesChapter 3. Describing Data-Numerical Measuressyed abdalNo ratings yet
- 24 Trig Identity ProblemsDocument4 pages24 Trig Identity ProblemsAldrean TinayaNo ratings yet
- M2V1 Chapter 6 Applications of Differentiation: Level 1 QuestionsDocument27 pagesM2V1 Chapter 6 Applications of Differentiation: Level 1 Questions15 15No ratings yet