Mechanical Properties, Structures

and Mechanical Analysis

Jing Wang

Electrical Engineering Department
University of South Florida
ENB 378, 4202 E. Fowler Avenue
Tampa, FL 33620
Tel: (813) 974-6011
e-mail: jingw@eng.usf.edu

Outline
As we discussed before, MEMS are made from mechanical
structures and we therefore need to understand how to
perform simple mechanical analysis to determine the
mechanical behavior of various MEMS devices.
The mechanical behavior depends not only on the size and
shape of the mechanical structure, but also on the material
used, the properties of that material, and how these
properties are affected by external effects such as
temperature and force.
So, in this series of lectures we will review the following:
Review of some relevant material properties
Review of basic relationships governing analysis of mechanical
systems under static conditions
Review of force-deflection behavior of some standard structures
Statics Review
The topic of statics deal with objects
or structures which are in
equilibrium, that is structures that
are at rest or in uniform, (non-
accelerated) motion. We will be
normally looking at structures which
are at rest.
For these structures we will be
interested in determining the forces
(loads and support reactions) acting
on the structure and forces acting
within members of the structure
(internal forces).
Draw Free Body Diagram
Apply the Conditions of Equilibrium

= 0
x
F

= 0
y
F

= 0
z
F

= 0
x
M

= 0
y
M

= 0
z
M
Normal Stress = Force per unit Area
H
W
A=WH
o = F / A = F / (WH)
Stress is a measurement of the intensity of the force in a
given material, over a specified cross-section.
Positive sign called tensile
Negative sign called compressive
Strain = fractional change in length
c = (L -L) / L = dL / L
Generalized Definition of Strain
More formal definition
Uniaxial strain:
(when cross-sectional area
not constant)






Microstrain = strain x10
-6

Can have strain along all
three directions.
c
x
=
u
x
(x + Ax) u
x
(x)
Ax
=
cu
x
cx
From: S. Senturia, Microsystem Design, Kluwer, 2000
x delta x
P
where u
x
is displacement in x-axis.
Poissons Ratio
Forces || to Surfaces Shear Stress
Normal and Shear Stress Components
for an Isotropic Solid
Isotropic = same elasticity in all directions
E
x
= E
y
= E
z
Add in off-axis strains from normal stresses in other directions
Important Special Case: Plane Stress
Plane Stress Case (cont.)
Linear Thermal Expansion
Many films deposited on Si or other substrates expand at different rates
as the temperature changes.
Many of these films are deposited at high temperatures, like LPCVD and
PECVD, but the devices are used at room temperature.
When the substrate is cooled down, some stress develops in the thin
film due to this mismatch in expansion/contraction
This can be understood and quantified by the Linear Thermal
Expansion Coefficient o, which is given by the ratio of the change in
strain to the change in temperature:


Note that as temperature changes strain builds up in the material, so:


o is sometime referred to as Coefficient of Thermal Expansion (CTE).
o
T
=
dc
x
dT
c
x
(T) =c
x
(T
0
)+o
T
AT
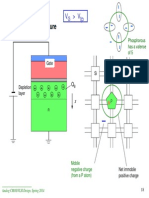
Thermal Stress
Ex.: Si/SiO
2
Mismatch Thermal Stress
From Microsystems Design, S. Senturia, Kluwer Publishing
Ex.: Si/SiO
2
Mismatch Thermal Stress
Given: o
Si
=2.810
-6
K
-1
,o
SiO2
= 0.710
-6
K
-1
,T
d
= 1200K,T
r
=300K, AT=300K


Strain: c
x
= -2.810
-6
K
-1
900K-(-0.710
-6
K
-1
900K) = -1.2610
-3

Stress: o
x
= E c
x
/ (1-v) = 69GPa

(-1.2610
-3
)

/(1-0.17)~-105MPa
Stress At the Ends Of A Patterned Layer
At the far end of the deposited thin film region, of course there is a
discontinuity because the forces to the left and right are not equal.
Therefore, shear forces develop that tend to pull the material back and
away from the edge, as shown below.
This could lead to delamination (i.e., peeling off) of the thin film from the
substrate if the adhesion of the thin film to the substrate is not very good.
Most films used in microfabrication have a good adhesion and seldom
delaminate, but sometimes the stresses could become quite large and
even with good adhesion could force the film to crack up and then
delaminate from the surface.
From Microsystems
Design, S. Senturia,
Kluwer Publishing
Residual Stresses in Thin Films
What is measured in a thin film (e.g., by the induced
substrate curvature) define as the residual stress

Thermal mismatch stress: well understood

What is not explained by thermal mismatch define as
the intrinsic (built-in) stress

Almost all thin films deposited on wafers to make MEMS
have some built-in stress. This stress could come from:

Deposition conditions: temperature, gas flows, compositions
Impurities and dopants causing defects in the material
Too much residue stress will
cause peeling of a thin film !!!
Even if the as-deposited film can
sustain the high residue stress,
after releasing the device might
buckle or crack !!!
~ 900 MPa compressive Stress
As-deposited
-Si Film (light)
The peel-off region
with exposed
substrate (dark)
The MEMS device crack after
releasing due to high stress
~ 600 MPa
Compressive
Stress
Problems Caused by Residual Stress
Measuring (Average) Residual Strain
Residual Strain Gradients
What to do About Stress?!
So, how can we fix stress problems in MEMS. We know there is stress
in the materials we use, and we know that many of the structures we
use are thin and long and so there is a high chance for buckling if we
use a bridge structure and the material has compressive stress.
Solutions:
Relieve the stress: the stress can be annealed out in many cases, or at
least be reduced. Sometimes, the stress can be reduced by changing of
process recipe (i.e. low-stress silicon-rich nitride). By reducing the stress, it
may be possible to avoid buckling and other stress related issues.
Combine films with opposite type of stress to compensate (OX/NITR/OX)
In choosing device dimensions, and designing the mechanical structures, we
have to account for the effects of stress, and so it is possible to make the
structures strong enough to tolerate some level of stress, and therefore not
buckle under the stress.
Or, we can use structures that because of their design allow the stress to be
relieved. We will discuss this further next.
Stress: Force per unit area acting on the surface of a differential
volume element of a solid body
Normal stress: forces perpendicular to a differential surface o
x
, o
y
, o
z

Shear stress: forces acting along the surface: t
xy
, t
yx
, t
yz
, t
zy
, t
xz
, t
zx
(note
that the first subscript identifies the face (surface perpendicular to the axis), and the
second subscript identifies the direction).

Static equilibrium (no net forces or torques)
Equal and opposite forces
Equal and opposite torques (shear)
t
xy
= t
yx
, t
yz
= t
zy,
t
xz
= t
zx

From: S. Senturia, Microsystem Design, Kluwer, 2000
Normal and Shear Stress Components of
An Infinitesimal Element & Its Equilibrium
Elastic Constants: Anisotropic Materials
Anisotropic materials like Si will not have the simple stress-strain relationships
discussed before. A more complex stress-strain relationship that depends on
orientation exists. This is described often in matrix form:








The C coefficients are called the stiffness coefficients.
It is also possible to define strain in terms of stress, in which case a matrix
inverse of C can be used and these are called compliance coefficients and are
typically referred to as S.
It is also possible to define strain in terms of stress, in which case the inverse of
matrix C can be used. This matrix is the S matrix and the coefficients are called
compliance coefficients. Therefore, again in short form, this can be written
as:



Note that the stiffness coefficients have the dimension of Youngs modulus
(Pascals), and the compliance coefficients have the dimensions of Pascals
-1
.
So, the above two relationships are completely mechanical relationships.
Note that these matrices have 36 entries, but only 21 independent components.
Things however, get easier for some of the materials, like Silicon, where many of
the entries become zero due to the specific symmetry of the material.
We will see that the same is true for Quartz, another crystalline material.

Elastic Constants: Anisotropic Materials
c
I
= S
IJ
o
J
J

Elastic Constants: Silicon

Fortunately because of the cubic symmetry of Si, this 6x6 matrix
simplifies to the following. Note that there are only three independent
quantities.
We will come back and visit this later on when we discuss piezo-
resistivity in Si.

Macro and Micro Suspensions
Springs in MEMS
Spring in MEMS (cont.)
Although there are many complex mechanical structures, there are a few that
are typically used most often in building MEMS.
Most commonly used structures are beams, bridges, and diaphragms.





It is not possible to present a detailed discussion of how to analyze and design
mechanical systems. We will only do a basic review of mechanics and discuss
only those cases that are of relevance to applications in MEMS.
If you need additional information, you should refer to introductory mechanics
books. Fortunately, much of the information that we will need to use in building
and analyzing MEMS is already available in standard forms and tabulated in
handbooks. For more detailed information one needs to take courses in
mechanical engineering.
Hookes Law
u=x
F=k.x
F= Applied Force
x = Distance traveled
k =Spring Constant
u= Displacement
F
u
x
Work Done
To move Spring
k
Spring is loaded down by a linear
force F
It moves by an amount u=x
Therefore, work has been done to
move the spring.
This work is equal to 1/2(F.x)
Axially-Loaded Beam
H
W
F
F
L
x
y
z

Axial Stress : o =
F
WH
Axial Strain : c =
o
E
=
F
EWH
oL =cL =
FL
EWH
But since:
F = kox
Spring Constant = k =
EWH
L
Force on the beam is axial, meaning the force is
applied along the long axis of the beam.
The stress and strain that the beam experiences
are shown on the right.
The beam will elongate upon application of the
force, and so it experiences positive strain.
Because of the strain, the beam also experiences
stress.
The stress is tensile stress.
If the force were applied in the opposite direction,
the strain would be negative and the stress would
be compressive.
Types of Support
Fixed Free
Fixed or clamped: The
beam cannot move vertically
or horizontally at the
support, and the slope of the
beam at the support is
always 0
Free: free to move
Pinned: The beam cannot
move vertically or
horizontally but the slope ca
be non-zero
Pinned on rollers: vertical
position is fixed, but
horizontal position and slope
can change.
Pinned Pinned on
Rollers
Fixed
Fixed
Types of Loads
Fixed Free
Pinned Pinned on
Rollers
q = Distributed load (uniform across
width of beam
L = length over which load is
distributed
P = pressure on beam
P = q*L
Width W
F = force per unit length of beam
W = Width of beam
F = total force acting at position x
F = F W
F
q
L
Forces and Moments
For equilibrium, zero total force
and moment on the beam.
Reaction force FR must be equal
and opposite the applied external
force.



Note that the moments and forces
can be calculated at any point x
along the beam:


We have external transverse
loads, shear forces, and moments
F
R
= F
M
Total
= M
R
F
R
L = 0
M
R
= FL = F
R
L

Shear Force V
x,r
= F =V
x,l
M
x,r
= F(L x) = M
x,l
From: S. Senturia, Microsystem Design, Kluwer, 2000
F is applied force
F
R
is reaction force
M
total
is total moment acting on the beam,
M
R
is reaction moment necessary to
assure zero rotation at the support
L is length of beam
V
x,r
is the shear force
A Cantilever Beam
Checking the Assumptions
Sign Conventions For Moments, Shear Forces

F
T
= qdx + (V + dV) V = 0 q =
dV
dx
M
T
= (M + dM) M (V + dV)dx
qdx
2
dx
If M
T
= 0 V =
dM
dx
The figure on the right explains
how loads, shear forces, and
moments are related, and their
sign conventions for a differential
beam element.
Positive moments cause the beam
element to bend upward with an
upward curvature.
Positive shear forces cause a
clockwise rotation.
The requirement for static
equilibrium requires that the total
force on the beam be zero:

Beam Segment in Pure Bending
Bending Moment M
z
Bending Strain and Beam Curvature
Curvature and Strain (cont.)
Flexural Rigidity (Moment of Inertia) I
z
Moment of Inertia
Note that for a thin, long, and relatively wide beam, of the type we will see often
in MEMS:
It is compliant (easy to bend) in the z direction, so I
z
is small
It is stiff and harder to bend in the y direction (so I
y
is larger)
Formulae for moment of inertia of different structures is available in standard
handbooks. See for example Roarks Formulas for Stress and Strain, by
Warren C. Young.
y
x
z
h
w
L

I
z
=
wh
3
12
I
y
=
hw
3
12
Boundary Conditions
The Cantilever with a Concentrated Load
Tip Deflection and Spring Constant
Types of Support
Fixed Free
Fixed or clamped: The
beam cannot move vertically
or horizontally at the
support, and the slope of the
beam at the support is
always 0
Free: free to move
Pinned: The beam cannot
move vertically or
horizontally but the slope ca
be non-zero
Pinned on rollers: vertical
position is fixed, but
horizontal position and slope
can change.
Pinned Pinned on
Rollers
Fixed
Fixed
Types of Loads
Fixed Free
Pinned Pinned on
Rollers
q = Distributed load (uniform across
width of beam
L = length over which load is
distributed
P = pressure on beam
P = q*L
Width W
F = force per unit length of beam
W = Width of beam
F = total force acting at position x
F = F W
F
q
L
Summary of Loading and Boundary Conditions
How to calculate spring constant
Series Combinations of Cantilevers
Parallel Combinations of Springs
Typical Support Springs/Beams
Cantilever: can relieve stress, is compliant, but is more susceptible to stiction, etc.
Bridge: very nice and strong support, takes a lot of area, susceptible to compressive stress
Crab Leg: it is a kind of bridge support, saves a lot of area over standard bridge, but still
susceptible to residual compressive stress
Folded Beam: relieves the stress, saves area, has a good stiffness to out of plane forces,
but is compliant lateral to surface.
Mass
Support
Beam
Support
Beam
Mass
Cantilever
Bridge
Mass
Crab Leg
Mass
Folded
Truss
Beams
Anchor
Folded-Flexure Suspension Variants
Folded Beams: Spring Constant
From William C. Tangs Ph.D. thesis, UC Berkeley
k
x
=
2Ehw
3
L
3
k
z
=
2Ewh
3
L
3
Stress is relieved through the
expansion/contraction of the quarter beam
sections.
The trusses are assumed stiff and do not
bend because they are wider.
There is not much deflection in the y direction
The ratio of the spring constants in the x and z
directions should be as large as possible

Need to make h >>w !!!
k
z
>> k
x
Forces and Moments
For equilibrium, zero total force
and moment on the beam.
Reaction force FR must be equal
and opposite the applied external
force.



Note that the moments and forces
can be calculated at any point x
along the beam:



We have external transverse
loads, shear forces, and moments
F
R
= F
M
Total
= M
R
F
R
L = 0
M
R
= FL = F
R
L
l x r x
l x r x
M x L F M
V F V
, ,
, ,
) (
: Force Shear
= =
= =
From: S. Senturia, Microsystem Design, Kluwer, 2000
F is applied force
F
R
is reaction force
M
total
is total moment acting on the beam,
M
R
is reaction moment necessary to
assure zero rotation at the support
L is length of beam
V
x,r
is the shear force
Elementary Solutions For Cantilever Beam
)
3
1 (
2
: result Final
0
0 ) 0 (
: conditions Boundary
) (
) (
2
) 0 (
2
2
L
x
x
EI
FL
w
dx
dw
w
x L
EI
F
dx
w d
x L F M
x
=
=
=
=
=
=
F
EI
LH H
x L
EI
F
L
EI
k
k
F
EI
L
w End
2 2
) (
1
: Strain
3
: Constant Spring
)
3
(
Beam at Deflection Max.
max
3
3
max
= =
=
=
=

We can determine the bending of a cantilever beam using the above equations
and for the specific boundary conditions, as shown below:

Force-Deflection Equations for Beams
From Micromachined Transducer
Sourcebook, G. Kovacs
F= Point Force
=Distributed Load
y=Deflection
x= position along
beam length
E= Youngs Modulus
I= Moment of Inertia
o=Stress
L= Beam Length
t= Beam Thickness
F
Comments
Detailed derivation of the solutions for the equation under different conditions is
provided in a number of different books.
Many of the standard conditions and structures we will face in MEMS systems
have been solved and standard equations for force-deflection and spring
constant of these microstructures are provided in standard mechanical
engineering handbooks. Some of these are provided at the end of the notes.
There are a few things to note about the discussion on previous pages:
The equation relating the radius of curvature and the moment is a simple and
fundamental relation that should be remembered.
To get deflection vs. moment, or force, the second order differential equation can be
solved with the boundary conditions shown. Note that at the fixed support, the beam
does not move, and its slope is zero.
We have ignored the effects of residual stress in this analysis. S. Senturia discusses
these in his book Microsystems Design, and you should review this carefully. It is
mostly a standard derivation and is not discussed here.
There are two parameters that one needs to know for any given mechanical structure:
the moment of inertia I, and the spring constant k. These have been derived for
most mechanical structures, such as beams, bridges, etc., and one can refer to
handbooks to obtain equations such as those used for a cantilever beam.
Residual stress is a very important and key parameter for many MEMS devices.
Typical Support Springs/Beams
Cantilever: can relieve stress, is compliant, but is more susceptible to stiction, etc.
Bridge: very nice and strong support, takes a lot of area, susceptible to compressive stress
Crab Leg: it is a kind of bridge support, saves a lot of area over standard bridge, but still
susceptible to residual compressive stress
Folded Beam: relieves the stress, saves area, has a good stiffness to out of plane forces,
but is compliant lateral to surface.
Mass
Support
Beam
Support
Beam
Mass
Cantilever
Bridge
Mass
Crab Leg
Mass
Folded
Truss
Beams
Anchor
Lateral Resonator Using Folded Beams (Top View)
From William C. Tangs Ph.D. thesis, UC Berkeley
Folded-beam Support
Suspended and Moving Shuttle Mass
Folded Beams: Spring Constant
From William C. Tangs Ph.D. thesis, UC Berkeley
k
x
=
2Ehw
3
L
3
k
z
=
2Ewh
3
L
3
Stress is relieved through the
expansion/contraction of the quarter beam
sections.
The trusses are assumed stiff and do not
bend because they are wider.
There is not much deflection in the y direction
The ratio of the spring constants in the x and z
directions should be as large as possible

Need to make h >>w !!!
k
z
>> k
x
Overall Spring Constant
Double-Folded Beam
It is possible to have a double folded beam in order to obtain even a larger compliance
in the x direction, as shown below. It is not important that you know how to do the
derivation, but you should have a basic understanding of the fact that indeed the beam
becomes more flexible in the x direction, since the overall length is larger, but that this
does not take up too much area since the beam has a double fold in it.
From William C. Tangs
Ph.D. thesis, UC Berkeley
GLASS SUBSTRATE
DRIVE COMB
ELECTRODES
ANCHOR TO SUBSTRATE &
LEAD TRANSFER FOR FRAME
SUPPORT BEAMS WITH METAL
LINES ON UNDERSIDE
SHUTTLE MASS WITH POLY
HEATER ON UNDERSIDE
METAL
INTERCONNECTS
PROBE TIP
OVERHANGING
THE GLASS SUBSTRATE
SILICON
SUBSTRATE
GOLD
POLYSILICON
THERMOCOUPLE
DIELECTRICS
TIP
METAL/DIELECTRIC
AIR BRIDGE
LEAD TRANSFER FOR
THERMOCOUPLE OR
POLY HEATER
Conductor 1
Insulator
Conductor 2
Thermocouple
Junction
Tip
SILICON
MICROMACHINED
THERMAL SENSOR
METAL
THERMAL SENSOR
Micromachined Scanning Thermal
Profilometer (STP)
Actuator
Temperature
Sensor
Resonant
Shuttle Mass
15m-Thick p++ Si-On-Glass
Integrated Thermopile For Temp. Sensor
Comb Resonators For Dithering Probe Tip
Spatial Resolution of ~3.3nm
NETD Of About 0.1 mHz
Electrostatic Comb Driven Resonators
15m-Thick p++ Si
Submicron Width
2m Capacitive Gaps
Surface Micromachined Lateral Resonators
Prof. Clark Nguyen, Univ. of Michigan
Selected Goals for Suspension Design