FOURIER

SERIES
FSTPi, UTHM
Fourier series were introduced by Joseph
Fourier (17681830) for the purpose of
solving the heat equation in a metal plate.

Fourier's idea was to model a complicated heat
source as a superposition (or linear combination)
of simple sine and cosine waves, and to write
the solution as a superposition of the
corresponding eigensolutions. This superposition
or linear combination is called the Fourier
series.
INTRODUCTION
FSTPi, UTHM
Although the original motivation was to solve the heat
equation, it later became obvious that the same
techniques could be applied to a wide array of
mathematical and physical problems, and especially those
involving linear differential equations with constant
coefficients, for which the eigensolutions are sinusoids. (wikipedia).
Concept
Given an infinite trigonometric series in form of
Fourier series enable us to represent a periodic function as
an infinite trigonometric series in sine and cosine terms.
0
1
1
( ) ( cos sin )
2
n n
n
f x a a nx b nx

=
= + +

We shall at first be concerned with the main question:

Given a function f, how do we calculate , and ?
0
a
n
a
n
b
FSTPi, UTHM
PERIODIC FUNCTIONS &
ODD AND EVEN FUNCTIONS
Fourier series can be used to represent very broad
classes of functions, but we will only focus for Fourier series
on periodic functions and how odd and even functions may
reduce the load of mathematical manipulation involved in
determining Fourier series.
Periodic function
A function f (x) is said to be periodic with period T if
( ) ( ) f x T f x + =
FSTPi, UTHM
-> odd function if f (x) and g (x) is different sign function.
Odd if f (-x) = - f (x) and the graph of f (x) symmetrical about
the origin
Odd and even function
Even if f (-x) = f (x) and the graph of f (x) symmetrical about
the y axis
Properties: products functions
For f (x) g (x), yields
-> even function if f (x) and g (x) both odd or both even
Example: Odd and Even
A function f (x) is said to be
Example: Odd and Even
FSTPi, UTHM
FOURIER SERIES FOR
PERIODIC FUNCTIONS
Periodic function 2l
Let a function f (x) is defined over the range l to l, i.e. has
a periodic interval 2l, then the Fourier series for f (x) is of the
form
0
1
1
( ) cos sin
2
n n
n
n x n x
f x a a b
l l
t t

=
| | | |
= + +
` | |
\ . \ . )

with
0
1
( ) ,
1
( ) cos , 1, 2,
1
( ) sin , 1, 2,
l
l
l
n
l
l
n
l
a f x dx
l
n x
a f x dx n
l l
n x
b f x dx n
l l
t
t

=
| |
= =
|
\ .
| |
= =
|
\ .
}
}
}
Fourier
coefficients
FSTPi, UTHM
f (x) is even function
Consider the Fourier series
for periodic function,
If f (x) is even function, then
the Fourier coefficient . 0
n
b =
Now, look at these case
f (x) is odd function
Consider the Fourier series
for periodic function,
If f (x) is odd function, then
the Fourier coefficients
and .
0
0 a =
0
n
a =
f (x) is neither odd nor even function
The Fourier series will contain ALL Fourier coefficients
Also known as Fourier sine
series.
Also known as Fourier cosine
series.
FSTPi, UTHM
How to find Fourier series?
Step 1
Sketch the graph of the given periodic function.
Step 2
Determine either the function is odd, even or neither
odd nor even.
Step 3
Find the Fourier coefficient(s)--> depends on type of
function.
Step 4
Substitute the Fourier coefficient(s) in Step 3 to get
Fourier series for the function.
Example: Fourier series for periodic function 1
Example: Fourier series for periodic function 2
FSTPi, UTHM
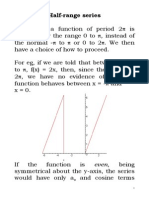
HALF-RANGE FOURIER SERIES
Sometimes a function is defined over the range 0 to l
that is half of the normal range -l to l. Fourier series
for f (x) may be expanded in a Fourier series for odd function,
even function or neither odd nor even.
The series produced is called half-range Fourier series.
The half-range Fourier series for f (x) is of the form
0
1
1
( ) cos sin
2
n n
n
n x n x
f x a a b
l l
t t

=
| | | |
= + +
` | |
\ . \ . )

with
0
0
0
0
2
( ) ,
2
( ) cos , 1, 2,
2
( ) sin , 1, 2,
l
l
n
l
n
a f x dx
l
n x
a f x dx n
l l
n x
b f x dx n
l l
t
t
=
| |
= =
|
\ .
| |
= =
|
\ .
}
}
}
FSTPi, UTHM
1
f (x) is expanded to odd function
--> Half range sine series
Consider these case
Consider the half-range Fourier series with the
Fourier coefficients and
0
n
a =
0
0 a =
2
f (x) is expanded to even function
--> Half range cosine series
Consider the half-range Fourier series with the Fourier
coefficients
0
n
b =
3
f (x) is expanded to neither odd or even function
Consider the ALL terms in half-range Fourier series
BUT the computation would be more difficult.
Example: Half-range Fourier series
FSTPi, UTHM
You try this!
Joseph Fourier (1768 1830)
Had crazy idea (1807) :
Any periodic function
can be written as sum
of sines and cosines of
different frequencies
Revision