Professional Documents
Culture Documents
Functions and Their Graphs
Uploaded by
ayadi_ezer6795Copyright
Available Formats
Share this document
Did you find this document useful?
Is this content inappropriate?
Report this DocumentCopyright:
Available Formats
Functions and Their Graphs
Uploaded by
ayadi_ezer6795Copyright:
Available Formats
The Cartesian Coordinate System
and Straight lines
Equations of Lines
Functions and Their Graphs
The Algebra of Functions
Linear Functions
Quadratic Functions
Functions and Mathematical Models
Functions and Their Graphs
2.1
The Cartesian Coordinate System
and Straight lines
1 1 2 2 3 3 4 4 5 5 6 6
(2, 5) (2, 5)
y y
x x
L L
A Ay y = = 4 4
A Ax x = 3 = 3
6 6
5 5
4 4
3 3
2 2
1 1
(5, 1) (5, 1)
4 3 2 1 0 1 2 3 4
We can represent real numbers geometrically by points on
a real number, or coordinate, line:
The Cartesian Coordinate System
The Cartesian Coordinate System
The Cartesian coordinate system extends this concept to a
plane (two dimensional space) by adding a vertical axis.
4 3 2 1 1 2 3 4
4
3
2
1
1
2
3
4
The Cartesian Coordinate System
The horizontal line is called the x-axis, and the vertical line is
called the y-axis.
4 3 2 1 1 2 3 4
4
3
2
1
1
2
3
4
x
y
The Cartesian Coordinate System
The point where these two lines intersect is called the origin.
4 3 2 1 1 2 3 4
4
3
2
1
1
2
3
4
x
y
Origin
The Cartesian Coordinate System
In the x-axis, positive numbers are to the right and negative
numbers are to the left of the origin.
4 3 2 1 1 2 3 4
4
3
2
1
1
2
3
4
x
y
Positive Direction Negative Direction
The Cartesian Coordinate System
In the y-axis, positive numbers are above and negative
numbers are below the origin.
4 3 2 1 1 2 3 4
4
3
2
1
1
2
3
4
x
y
P
o
s
i
t
i
v
e
D
i
r
e
c
t
i
o
n
N
e
g
a
t
i
v
e
D
i
r
e
c
t
i
o
n
(
2, 4)
(1,
2)
(4, 3)
The Cartesian Coordinate System
A point in the plane can now be represented uniquely in this
coordinate system by an ordered pair of numbers (x, y).
4 3 2 1 1 2 3 4
4
3
2
1
1
2
3
4
x
y
(3, 1)
The Cartesian Coordinate System
The axes divide the plane into four quadrants as shown below.
4 3 2 1 1 2 3 4
4
3
2
1
1
2
3
4
x
y
Quadrant I
(+, +)
Quadrant II
(, +)
Quadrant IV
(+, )
Quadrant III
(, )
Slope of a Vertical Line
Let L denote the unique straight line that passes through
the two distinct points (x
1
, y
1
) and (x
2
, y
2
).
If x
1
= x
2
, then L is a vertical line, and the slope is
undefined.
(x
1
, y
1
)
(x
2
, y
2
)
y
x
L
Slope of a Nonvertical Line
If (x
1
, y
1
) and (x
2
, y
2
) are two distinct points on a
nonvertical line L, then the slope m of L is given by
(x
1
, y
1
)
(x
2
, y
2
)
y
x
2 1
2 1
y y y
m
x x x
A
= =
A
L
y
2
y
1
= Ay
x
2
x
1
= Ax
Slope of a Nonvertical Line
If m > 0, the line slants upward from left to right.
x
L
Ay = 1
Ax = 1
m = 1
y
Slope of a Nonvertical Line
If m > 0, the line slants upward from left to right.
y
x
L
Ay = 2
Ax = 1
m = 2
m = 1
Slope of a Nonvertical Line
If m < 0, the line slants downward from left to right.
x
L
Ay = 1
Ax = 1
y
m = 2
Slope of a Nonvertical Line
If m < 0, the line slants downward from left to right.
y
x
L
Ay = 2
Ax = 1
1 2 3 4 5 6
(2, 5)
Examples
Sketch the straight line that passes through the point
(2, 5) and has slope 4/3.
Solution
1. Plot the point (2, 5).
2. A slope of 4/3 means
that if x increases by 3,
y decreases by 4.
3. Plot the resulting
point (5, 1).
4. Draw a line through
the two points.
y
x
L
Ay = 4
Ax = 3
6
5
4
3
2
1
(5, 1)
Examples
Find the slope m of the line that goes through the points
(1, 1) and (5, 3).
Solution
Choose (x
1
, y
1
) to be (1, 1) and (x
2
, y
2
) to be (5, 3).
With x
1
= 1, y
1
= 1, x
2
= 5, y
2
= 3, we find
2 1
2 1
3 1 2 1
5 ( 1) 6 3
y y
m
x x
= = = =
Examples
Find the slope m of the line that goes through the points
(2, 5) and (3, 5).
Solution
Choose (x
1
, y
1
) to be (2, 5) and (x
2
, y
2
) to be (3, 5).
With x
1
= 2, y
1
= 5, x
2
= 3, y
2
= 5, we find
2 1
2 1
5 5 0
0
3 ( 2) 5
y y
m
x x
= = = =
2 1 1 2 3 4
Examples
Find the slope m of the line that goes through the points
(2, 5) and (3, 5).
Solution
The slope of a horizontal line is zero:
y
x
L
6
4
3
2
1
(2, 5)
(3, 5)
m = 0
Parallel Lines
Two distinct lines are parallel if and only if their
slopes are equal or their slopes are undefined.
Example
Let L
1
be a line that passes through the points (2, 9) and
(1, 3), and let L
2
be the line that passes through the points
(
4, 10) and (3,
4).
Determine whether L
1
and L
2
are parallel.
Solution
The slope m
1
of L
1
is given by
The slope m
2
of L
2
is given by
Since m
1
= m
2
, the lines L
1
and L
2
are in fact parallel.
1
3 9
2
1 ( 2)
m
= =
2
4 10
2
3 ( 4)
m
= =
2.2
Equations of Lines
1 1 2 2 3 3 4 4 5 5 6 6
(0, (0, 3) 3)
y y
x x
L L
1 1
1 1
2 2
3 3
4 4
(4, 0) (4, 0)
Equations of Lines
Let L be a straight line
parallel to the y-axis.
Then L crosses the x-axis at
some point (a, 0) , with the
x-coordinate given by x = a,
where a is a real number.
Any other point on L has
the form (a, ), where
is an appropriate number.
The vertical line L can
therefore be described as
x = a
(a, )
y
x
L
(a, 0)
y y
y
Equations of Lines
Let L be a nonvertical line with a slope m.
Let (x
1
, y
1
) be a fixed point lying on L, and let (x, y) be a
variable point on L distinct from (x
1
, y
1
).
Using the slope formula by letting (x, y) = (x
2
, y
2
), we get
Multiplying both sides by x x
1
we get
1
1
y y
m
x x
1 1
( ) y y m x x =
Point-Slope Form
1 1
( ) y y m x x =
An equation of the line that has slope m and
passes through point (x
1
, y
1
) is given by
Examples
Find an equation of the line that passes through the point
(1, 3) and has slope 2.
Solution
Use the point-slope form
Substituting for point (1, 3) and slope m = 2, we obtain
Simplifying we get
1 1
( ) y y m x x =
3 2( 1) y x =
2 1 0 x y + =
Examples
Find an equation of the line that passes through the points
(3, 2) and (4, 1).
Solution
The slope is given by
Substituting in the point-slope form for point (4, 1) and
slope m = 3/7, we obtain
3
1 ( 4)
7
y x + =
3 7 5 0 x y + =
2 1
2 1
1 2 3
4 ( 3) 7
y y
m
x x
= = =
7 7 3 12 y x + = +
Perpendicular Lines
If L
1
and L
2
are two distinct nonvertical lines that
have slopes m
1
and m
2
, respectively, then L
1
is
perpendicular to L
2
(written L
1
L
2
) if and only if
1
2
1
m
m
=
Example
Find the equation of the line L
1
that passes through the
point (3, 1) and is perpendicular to the line L
2
described by
Solution
L
2
is described in point-slope form, so its slope is m
2
= 2.
Since the lines are perpendicular, the slope of L
1
must be
m
1
= 1/2
Using the point-slope form of the equation for L
1
we obtain
3 2( 1) y x =
1
1 ( 3)
2
2 2 3
2 5 0
y x
y x
x y
=
= +
+ =
(a, 0)
(0, b)
Crossing the Axis
A straight line L that is neither horizontal nor vertical
cuts the x-axis and the y-axis at, say, points (a, 0) and
(0, b), respectively.
The numbers a and b are called the x-intercept and
y-intercept, respectively, of L.
y
x
L
y-intercept
x-intercept
Slope-Intercept Form
An equation of the line that has slope m and
intersects the y-axis at the point (0, b) is given by
y = mx + b
Examples
Find the equation of the line that has slope 3 and
y-intercept of 4.
Solution
We substitute m = 3 and b = 4 into y = mx + b and get
y = 3x 4
Examples
Determine the slope and y-intercept of the line whose
equation is 3x 4y = 8.
Solution
Rewrite the given equation in the slope-intercept form.
Comparing to y = mx + b, we find that m = and b =
2.
So, the slope is and the y-intercept is
2.
3 4 8
4 8 3
3
2
4
x y
y x
y x
=
=
=
Applied Example
Suppose an art object purchased for $50,000 is expected to
appreciate in value at a constant rate of $5000 per year for
the next 5 years.
Write an equation predicting the value of the art object for
any given year.
What will be its value 3 years after the purchase?
Solution
Let x = time (in years) since the object was purchased
y = value of object (in dollars)
Then, y = 50,000 when x = 0, so the y-intercept is b = 50,000.
Every year the value rises by 5000, so the slope is m = 5000.
Thus, the equation must be y = 5000x + 50,000.
After 3 years the value of the object will be $65,000:
y = 5000(3) + 50,000 = 65,000
General Form of a Linear Equation
The equation
Ax + By + C = 0
where A, B, and C are constants and A and B
are not both zero, is called the general form
of a linear equation in the variables x and y.
General Form of a Linear Equation
An equation of a straight line is a linear
equation; conversely, every linear equation
represents a straight line.
Example
Sketch the straight line represented by the equation
3x 4y 12 = 0
Solution
Since every straight line is uniquely determined by two
distinct points, we need find only two such points through
which the line passes in order to sketch it.
For convenience, lets compute the x- and y-intercepts:
Setting y = 0, we find x = 4; so the x-intercept is 4.
Setting x = 0, we find y = 3; so the y-intercept is 3.
Thus, the line goes through the points (4, 0) and (0, 3).
Example
Sketch the straight line represented by the equation
3x 4y 12 = 0
Solution
Graph the line going through the points (4, 0) and (0, 3).
1 2 3 4 5 6
(0, 3)
y
x
L
1
1
2
3
4
(4, 0)
Equations of Straight Lines
Vertical line: x = a
Horizontal line: y = b
Point-slope form: y y
1
= m(x x
1
)
Slope-intercept form: y = mx + b
General Form: Ax + By + C = 0
2.3
Functions and Their Graphs
( ) f x x = ( )
f x x =
( ) f x x = ( )
f x x =
3 3 2 2 1 1 1 1 2 2 3 3
3 3
2 2
1 1
x x
y y
Functions
A function f is a rule that assigns to each element in a
set A one and only one element in a set B.
The set A is called the domain of the function.
It is customary to denote a function by a letter of the
alphabet, such as the letter f.
If x is an element in the domain of a function f, then the
element in B that f associates with x is written f(x) (read
f of x) and is called the value of f at x.
The set B comprising all the values assumed by y = f(x)
as x takes on all possible values in its domain is called
the range of the function f.
Example
Let the function f be defined by the rule
Find: f(1)
Solution:
( )
2
2 1 f x x x = +
( ) ( ) ( )
2
1 2 1 1 1 2 1 1 2 f = + = + =
Example
Let the function f be defined by the rule
Find: f( 2)
Solution:
( )
2
2 1 f x x x = +
( ) ( ) ( )
2
2 2 2 2 1 8 2 1 11 f = + = + + =
Example
Let the function f be defined by the rule
Find: f(a)
Solution:
( )
2
2 1 f x x x = +
( ) ( ) ( )
2
2
2 1 2 1 f a a a a a = + = +
Example
Let the function f be defined by the rule
Find: f(a + h)
Solution:
( )
2
2 1 f x x x = +
( ) ( ) ( )
2
2 2
2 1 2 4 2 1 f a h a h a h a ah h a h + = + + + = + + +
Applied Example
ThermoMaster manufactures an indoor-outdoor
thermometer at its Mexican subsidiary.
Management estimates that the profit (in dollars)
realizable by ThermoMaster in the manufacture and sale
of x thermometers per week is
Find ThermoMasters weekly profit if its level of
production is:
a. 1000 thermometers per week.
b. 2000 thermometers per week.
( )
2
0.001 8 5000 P x x x = +
Applied Example
Solution
We have
a. The weekly profit by producing 1000 thermometers is
or $2,000.
b. The weekly profit by producing 2000 thermometers is
or $7,000.
( ) ( ) ( )
2
1000 0.001 1000 8 1000 5000 2000 P = + = =
( ) ( ) ( )
2
2000 0.001 2000 8 2000 5000 7000 P = + = =
( )
2
0.001 8 5000 P x x x = +
Determining the Domain of a Function
Suppose we are given the function y = f(x).
Then, the variable x is called the independent variable.
The variable y, whose value depends on x, is called the
dependent variable.
To determine the domain of a function, we need to find
what restrictions, if any, are to be placed on the
independent variable x.
In many practical problems, the domain of a function is
dictated by the nature of the problem.
x
16 2x
Applied Example: Packaging
An open box is to be made from a rectangular piece of
cardboard 16 inches wide by cutting away identical
squares (x inches by x inches) from each corner and
folding up the resulting flaps.
10 10 2x
16
x
x x
Applied Example: Packaging
An open box is to be made from a rectangular piece of
cardboard 16 inches wide by cutting away identical
squares (x inches by x inches) from each corner and
folding up the resulting flaps.
a. Find the expression that gives the volume V of the box as
a function of x.
b. What is the domain of the function?
The dimensions of the
resulting box are:
x
16 2x
10 2x
x
16 2x
Applied Example: Packaging
Solution
a. The volume of the box is given by multiplying its
dimensions (length width height), so:
10 2x
( ) ( ) ( )
( )
2
3 2
16 2 10 2
160 52 4
4 52 160
V f x x x x
x x x
x x x
= =
= +
= +
Applied Example: Packaging
Solution
b. Since the length of each side of the box must be greater
than or equal to zero, we see that
must be satisfied simultaneously. Simplified:
All three are satisfied simultaneously provided that:
Thus, the domain of the function f is the interval [0, 5].
8 5 0 x x x s s > =
16 2 0 10 2 0 0 x x x > > >
0 5 x s s
More Examples
Find the domain of the function:
Solution
Since the square root of a negative number is undefined, it
is necessary that x 1 > 0.
Thus the domain of the function is [1,).
( )
1 f x x =
More Examples
Find the domain of the function:
Solution
Our only constraint is that you cannot divide by zero, so
Which means that
Or more specifically x 2 and x 2.
Thus the domain of f consists of the intervals (
, 2),
(2, 2), (2, ).
2
4 0 x =
( )
2
1
4
f x
x
=
( )( )
2
4 2 2 0 x x x = + =
More Examples
Find the domain of the function:
Solution
Here, any real number satisfies the equation, so the
domain of f is the set of all real numbers.
( )
2
3 f x x = +
Graphs of Functions
If f is a function with domain A, then corresponding to
each real number x in A there is precisely one real
number f(x).
Thus, a function f with domain A can also be defined as
the set of all ordered pairs (x, f(x)) where x belongs to A.
The graph of a function f is the set of all points (x, y) in
the xy-plane such that x is in the domain of f and y = f(x).
Example
The graph of a function f is shown below:
x
y
Domain
Range
x
y
(x, y)
Example
The graph of a function f is shown below:
What is the value of f(2)?
x
y
4
3
2
1
1
2
(2, 2)
1 2 3 4 5 6 7 8
Example
The graph of a function f is shown below:
What is the value of f(5)?
x
y
(5, 3)
4
3
2
1
1
2
1 2 3 4 5 6 7 8
Example
The graph of a function f is shown below:
What is the domain of f(x)?
x
y
4
3
2
1
1
2
Domain: [1,8]
1 2 3 4 5 6 7 8
Example
The graph of a function f is shown below:
What is the range of f(x)?
x
y
4
3
2
1
1
2
Range:
[2,4]
1 2 3 4 5 6 7 8
Example: Sketching a Graph
Sketch the graph of the function defined by the equation
y = x
2
+ 1
Solution
The domain of the function is the set of all real numbers.
Assign several values to the variable x and compute the
corresponding values for y:
x y
3 10
2 5
1 2
0 1
1 2
2 5
3 10
3 2 1 1 2 3
10
8
6
4
2
Example: Sketching a Graph
Sketch the graph of the function defined by the equation
y = x
2
+ 1
Solution
The domain of the function is the set of all real numbers.
Then plot these values in a graph:
x
y
x y
3 10
2 5
1 2
0 1
1 2
2 5
3 10
3 2 1 1 2 3
10
8
6
4
2
Example: Sketching a Graph
Sketch the graph of the function defined by the equation
y = x
2
+ 1
Solution
The domain of the function is the set of all real numbers.
And finally, connect the dots:
x
y
x y
3 10
2 5
1 2
0 1
1 2
2 5
3 10
Example: Sketching a Graph
Sketch the graph of the function defined by the equation
Solution
The function f is defined in a piecewise fashion on the set
of all real numbers.
In the subdomain ( , 0), the rule for f is given by
In the subdomain [0, ), the rule for f is given by
( )
if 0
if 0
x x
f x
x x
<
=
>
( )
f x x =
( )
f x x =
Example: Sketching a Graph
Sketch the graph of the function defined by the equation
Solution
Substituting negative values for x into , while
substituting zero and positive values into we get:
( )
if 0
if 0
x x
f x
x x
<
=
>
( )
f x x =
( )
f x x =
x y
3 3
2 2
1 1
0 0
1 1
2 1.41
3 1.73
Example: Sketching a Graph
Sketch the graph of the function defined by the equation
Solution
Plotting these data and graphing we get:
( )
if 0
if 0
x x
f x
x x
<
=
>
( )
f x x =
( )
f x x =
3 2 1 1 2 3
3
2
1
x
y
x y
3 3
2 2
1 1
0 0
1 1
2 1.41
3 1.73
The Vertical Line Test
A curve in the xy-plane is the graph of a function
y = f(x) if and only if each vertical line intersects it
in at most one point.
Examples
Determine if the curve in the graph is a function of x:
Solution
The curve is indeed a function of x, because there is one
and only one value of y for any given value of x.
x
y
Examples
Determine if the curve in the graph is a function of x:
Solution
The curve is not a function of x, because there is more than
one value of y for some values of x.
x
y
Examples
Determine if the curve in the graph is a function of x:
Solution
The curve is indeed a function of x, because there is one
and only one value of y for any given value of x.
x
y
2.4
The Algebra of Functions
1990 1990 1992 1992 1994 1994 1996 1996 1998 1998 2000 2000
2000 2000
1800 1800
1600 1600
1400 1400
1200 1200
1000 1000
t t
y y
B
i
l
l
i
o
n
s
o
f
D
o
l
l
a
r
s
B
i
l
l
i
o
n
s
o
f
D
o
l
l
a
r
s
Year Year
y y = = S S( (t t) )
y y = = R R( (t t) )
t t
R R( (t t) )
S S( (t t) )
The Sum, Difference, Product and Quotient
of Functions
Consider the graph below:
R(t) denotes the federal government revenue at any time t.
S(t) denotes the federal government spending at any time t.
1990 1992 1994 1996 1998 2000
2000
1800
1600
1400
1200
1000
t
y
B
i
l
l
i
o
n
s
o
f
D
o
l
l
a
r
s
Year
y = S(t)
y = R(t)
t
R(t)
S(t)
D(t) = R(t) S(t)
The Sum, Difference, Product and Quotient
of Functions
Consider the graph below:
The difference R(t) S(t) gives the budget deficit (if negative)
or surplus (if positive) in billions of dollars at any time t.
1990 1992 1994 1996 1998 2000
2000
1800
1600
1400
1200
1000
t
y
B
i
l
l
i
o
n
s
o
f
D
o
l
l
a
r
s
Year
y = S(t)
y = R(t)
t
R(t)
S(t)
The Sum, Difference, Product and Quotient
of Functions
The budget balance D(t) is shown below:
D(t) is also a function that denotes the federal government
deficit (surplus) at any time t.
This function is the difference of the two functions R and S.
D(t) has the same domain as R(t) and S(t).
1992 1994 1996 1998 2000
400
200
0
200
400
t
y
B
i
l
l
i
o
n
s
o
f
D
o
l
l
a
r
s
Year
t
D(t)
y = D(t)
The Sum, Difference, Product and Quotient
of Functions
Most functions are built up from other, generally
simpler functions.
For example, we may view the function f(x) = 2x + 4
as the sum of the two functions g(x) = 2x and h(x) = 4.
( )
( )
( )
f f x
x
g g x
| |
=
|
\ .
The Sum, Difference, Product and Quotient of Functions
Let f and g be functions with domains A and B, respectively.
The sum f + g, the difference f g, and the product fg of f
and g are functions with domain A B and rule given by
(f + g)(x) = f(x) + g(x) Sum
(f g)(x) = f(x) g(x) Difference
(fg)(x) = f(x)g(x) Product
The quotient f/g of f and g has domain A B excluding all
numbers x such that g(x) = 0 and rule given by
Quotient
Example
Let and g(x) = 2x + 1.
Find the sum s, the difference d, the product p, and the
quotient q of the functions f and g.
Solution
Since the domain of f is A = [1,) and the domain of g
is B = ( , ), we see that the domain of s, d, and p is
A B = [1,).
The rules are as follows:
( ) 1 f x x = +
( )
( ) ( )( ) ( ) ( ) 1 2 1
( ) ( )( ) ( ) ( ) 1 2 1
( ) ( )( ) ( ) ( ) 2 1 1
s x f g x f x g x x x
d x f g x f x g x x x
p x fg x f x g x x x
= + = + = + + +
= = = +
= = = + +
Example
Let and g(x) = 2x + 1.
Find the sum s, the difference d, the product p, and the
quotient q of the functions f and g.
Solution
The domain of the quotient function is [1,) together
with the restriction x
.
Thus, the domain is [1,
) Y (
,).
The rule is as follows:
( ) 1 f x x = +
( ) 1
( ) ( )
( ) 2 1
f f x x
q x x
g g x x
| | +
= = =
|
+
\ .
Applied Example: Cost Functions
Suppose Puritron, a manufacturer of water filters, has a
monthly fixed cost of $10,000 and a variable cost of
0.0001x
2
+ 10x (0 s x s 40,000)
dollars, where x denotes the number of filters
manufactured per month.
Find a function C that gives the total monthly cost
incurred by Puritron in the manufacture of x filters.
Applied Example: Cost Functions
Solution
Puritrons monthly fixed cost is always $10,000, so it can
be described by the constant function:
F(x) = 10,000
The variable cost can be described by the function:
V(x) =
0.0001x
2
+ 10x
The total cost is the sum of the fixed cost F and the
variable cost V:
C(x) = V(x) + F(x)
=
0.0001x
2
+ 10x + 10,000 (0 s x s 40,000)
Applied Example: Cost Functions
Lets now consider profits
Suppose that the total revenue R realized by Puritron from
the sale of x water filters is given by
R(x) =
0.0005x
2
+ 20x (0 x 40,000)
Find
a. The total profit function for Puritron.
b. The total profit when Puritron produces 10,000 filters per
month.
Applied Example: Cost Functions
Solution
a. The total profit P realized by the firm is the difference
between the total revenue R and the total cost C:
P(x) = R(x) C(x)
= (
0.0005x
2
+ 20x) (
0.0001x
2
+ 10x + 10,000)
=
0.0004x
2
+ 10x 10,000
b. The total profit realized by Puritron when producing 10,000
filters per month is
P(x) =
0.0004(10,000)
2
+ 10(10,000) 10,000
= 50,000
or $50,000 per month.
The Composition of Two Functions
Another way to build a function from other functions is
through a process known as the composition of functions.
Consider the functions f and g:
Evaluating the function g at the point f(x), we find that:
This is an entirely new function, which we could call h:
2
( ) 1 f x x = ( ) g x x =
( )
2
( ) ( ) 1 g f x f x x = =
2
( ) 1 h x x =
The Composition of Two Functions
Let f and g be functions.
Then the composition of g and f is the function
ggf (read g circle f ) defined by
(ggf )(x) = g(f(x))
The domain of ggf is the set of all x in the
domain of f such that f(x) lies in the domain of g.
Example
Let
Find:
a. The rule for the composite function ggf.
b. The rule for the composite function fgg.
Solution
To find ggf, evaluate the function g at f(x):
To find fgg, evaluate the function f at g(x):
2
( ) 1 ( ) 1 an d . f x x g x x = = +
2
( )( ) ( ( )) ( ) 1 1 1 g f x g f x f x x = = + = +
2 2
( )( ) ( ( )) ( ( )) 1 ( 1) 1
2 1 1 2
f g x f g x g x x
x x x x
= = = +
= + + = +
Applied Example: Automobile Pollution
An environmental impact study conducted for the city of
Oxnard indicates that, under existing environmental
protection laws, the level of carbon monoxide (CO)
present in the air due to pollution from automobile
exhaust will be 0.01x
2/3
parts per million when the
number of motor vehicles is x thousand.
A separate study conducted by a state government agency
estimates that t years from now the number of motor
vehicles in Oxnard will be 0.2t
2
+ 4t + 64 thousand.
Find:
a. An expression for the concentration of CO in the air due
to automobile exhaust t years from now.
b. The level of concentration 5 years from now.
Applied Example: Automobile Pollution
Solution
Part (a):
The level of CO is described by the function
g(x) = 0.01x
2/3
where x is the number (in thousands) of motor vehicles.
In turn, the number (in thousands) of motor vehicles is
described by the function
f(t) = 0.2t
2
+ 4t + 64
where t is the number of years from now.
Therefore, the concentration of CO due to automobile
exhaust t years from now is given by
(ggf )(t) = g(f(t)) = 0.01(0.2t
2
+ 4t + 64)
2/3
Applied Example: Automobile Pollution
Solution
Part (b):
The level of CO five years from now is:
(ggf )(5) = g(f(5)) = 0.01[0.2(5)
2
+ 4(5) + 64]
2/3
= (0.01)89
2/3
0.20
or approximately 0.20 parts per million.
2.5
Linear Functions
1 1 1 1 2 2 3 3 4 4 5 5
5 5
4 4
3 3
2 2
1 1
y y
x x
(1, 2) (1, 2)
L L
1 1
L L
2 2
Linear Function
The function f defined by
where m and b are constants, is called a linear
function.
( ) f x mx b = +
Applied Example: Linear Depreciation
A Web server has an original value of $10,000 and is to
be depreciated linearly over 5 years with a $3000 scrap
value.
Find an expression giving the book value at the end of
year t.
What will be the book value of the server at the end of
the second year?
What is the rate of depreciation of the server?
Applied Example: Linear Depreciation
Solution
Let V(t) denote the Web servers book value at the end of
the tth year. V is a linear function of t.
To find an equation of the straight line that represents the
depreciation, observe that V = 10,000 when t = 0; this tells
us that the line passes through the point (0, 10,000).
Similarly, the condition that V = 3000 when t = 5 says that
the line also passes through the point (5, 3000).
Thus, the slope of the line is given by
10, 000 3000 7000
1400
0 5 5
m
= = =
Applied Example: Linear Depreciation
Solution
Using the point-slope form of the equation of a line with
point (0, 10,000) and slope m = 1400, we obtain the
required expression
The book value at the end of the second year is given by
or $7200.
The rate of depreciation of the server is given by the
negative slope of the depreciation line m = 1400, so the
rate of depreciation is $1400 per year.
10, 000 1400( 0)
1400 10, 000
V t
V t
=
= +
(2) 1400(2) 10, 000 7200 V = + =
Applied Example: Linear Depreciation
Solution
The graph of V is:
1400 10,000 V t = +
1 2 3 4 5 6
(0, 10,000)
V
t
(5, 3000)
10,000
3000
Cost, Revenue, and Profit Functions
Let x denote the number of units of a product
manufactured or sold.
Then, the total cost function is
C(x) = Total cost of manufacturing x units
of the product
The revenue function is
R(x) = Total revenue realized from the sale
of x units of the product
The profit function is
P(x) = Total profit realized from
manufacturing and selling x units of
the product
Applied Example: Profit Function
Puritron, a manufacturer of water filters, has a monthly
fixed cost of $20,000, a production cost of $20 per unit, and
a selling price of $30 per unit.
Find the cost function, the revenue function, and the
profit function for Puritron.
Solution
Let x denote the number of units produced and sold.
Then,
( ) 20 20, 000 C x x = +
( ) 30 R x x =
( ) ( ) ( )
30 (20 20, 000)
10 20, 000
P x R x C x
x x
x
=
= +
=
Finding the Point of Intersection
Suppose we are given two straight lines L
1
and L
2
with
equations
y = m
1
x + b
1
and y = m
2
x + b
2
(where m
1
, b
1
, m
2
, and b
2
are constants) that intersect at the
point P(x
0
, y
0
).
The point P(x
0
, y
0
) lies on the line L
1
and so satisfies the
equation y = m
1
x + b
1
.
The point P(x
0
, y
0
) also lies on the line L
2
and so satisfies
y = m
2
x + b
2
as well.
Therefore, to find the point of intersection P(x
0
, y
0
) of the
lines L
1
and L
2
, we solve for x and y the system composed
of the two equations
y = m
1
x + b
1
and y = m
2
x + b
2
Example
Find the point of intersection of the straight lines that have
equations
y = x + 1 and y =
2x + 4
Solution
Substituting the value y as given in the first equation into
the second equation, we obtain
Substituting this value of x into either one of the given
equations yields y = 2.
Therefore, the required point of intersection is (1, 2).
1 2 4 x x + = +
3 3 x =
1 x =
1 1
2
3
4 5
5
4
3
2
1
Example
Find the point of intersection of the straight lines that have
equations
y = x + 1 and y =
2x + 4
Solution
The graph shows the point of intersection (1, 2) of the two
lines:
y
x
(1, 2)
L
1
L
2
Applied Example: Break-Even Level
Prescott manufactures its products at a cost of $4 per unit
and sells them for $10 per unit.
If the firms fixed cost is $12,000 per month, determine the
firms break-even point.
Solution
The revenue function R and the cost function C are given
respectively by
Setting R(x) = C(x), we obtain
( ) 10 ( ) 4 12, 000 d an . R x x C x x = = +
10 4 12, 000 x x = +
6 12, 000 x =
2000 x =
Applied Example: Break-Even Level
Prescott manufactures its products at a cost of $4 per unit
and sells them for $10 per unit.
If the firms fixed cost is $12,000 per month, determine the
firms break-even point.
Solution
Substituting x = 2000 into R(x) = 10x gives
So, Prescotts break-even point is 2000 units of the product,
resulting in a break-even revenue of $20,000 per month.
(2000) 10(2000) 20, 000 R = =
2.6
Quadratic Functions
1 1 1 1 2 2
1 1
1 1
2 2
x x
y y
2
( ) 2 5 2 f x x x = +
2
( ) 2 5 2 f x x x = +
Vertex Vertex
x x- -intercepts intercepts
1
2
1
2
5 9
,
4 8
| |
|
\ .
5 9
,
4 8
| |
|
\ .
y y- -intercept intercept
Quadratic Functions
A quadratic function is one of the form
where a, b, and c are constants and a 0.
For example, the function
is quadratic, with a = 2, b =
4, and c = 3.
2
( ) f x ax bx c = + +
2
( ) 2 4 3 f x x x = +
Quadratic Functions
Below is the graph of the quadratic function
The graph of a quadratic function is a curve called a
parabola that opens upward or downward.
2
( ) 2 4 3 f x x x = +
2
1 1 2 3 4
10
8
6
4
2
x
y
2
( ) 2 4 3 f x x x = +
Parabola
Quadratic Functions
The parabola is symmetric with respect to a vertical
line called the axis of symmetry.
The axis of symmetry also passes through the lowest or
highest point of the parabola, which is called the vertex
of the parabola.
2
1 1 2 3 4
10
8
6
4
2
x
y
Axis of
symmetry
Vertex (1, 1)
2
( ) 2 4 3 f x x x = +
Parabola
Quadratic Functions
We can use these properties to help us sketch the graph
of a quadratic function.
Suppose we want to sketch the graph of
If we complete the square in x, we obtain
Note that (x 1)
2
is nonnegative: it equals to zero when x = 1
and is greater than zero if x 1.
Thus, we see that f(x) >
2 for all values of x.
This tells us the vertex of the parabola is the point (1,
2).
2
( ) 3 6 1 f x x x = +
2
2 2
2
( ) 3( 2 ) 1
3[ 2 ( 1) ] 1 3
3( 1) 2
f x x x
x x
x
= +
= + +
=
Quadratic Functions
We know the vertex of the parabola is the point (1,
2) and
that it is the minimum point of the graph, since f(x) >
2 for
all values of x.
Thus, the graph of f(x) = 3x
2
6x +1 looks as follows:
2 2 4
4
2
2
x
y
2
( ) 3 6 1 f x x x = +
Vertex (1, 2)
Properties of Quadratic Functions
Given f(x) = ax
2
+ bx +c (a 0)
1. The domain of f is the set of all real numbers.
2. If a > 0, the parabola opens upward, and if a < 0,
it opens downward.
3. The vertex of the parabola is
4. The axis of symmetry of the parabola is
5. The x-intercepts (if any) are found by solving
f(x) = 0. The y-intercept is f(0) = c.
,
2 2
b b
f
a a
| |
| |
|
|
\ .
\ .
.
2
b
x
a
= .
Example
Given the quadratic function f(x) =
2x
2
+ 5x 2
a. Find the vertex of the parabola.
b. Find the x-intercepts (if any) of the parabola.
c. Sketch the parabola.
Solution
a. Here a =
2, b = 5, and c =
2. therefore, the x-coordinate
of the vertex of the parabola is
The y-coordinate of the vertex is therefore given by
Thus, the vertex of the parabola is the point
5 5
2 2( 2) 4
b
a
= =
2
5 5 5 9
2 5 2
4 4 4 8
f
| | | | | |
= + =
| | |
\ . \ . \ .
5 9
,
4 8
| |
|
\ .
.
Example
Given the quadratic function f(x) =
2x
2
+ 5x 2
a. Find the vertex of the parabola.
b. Find the x-intercepts (if any) of the parabola.
c. Sketch the parabola.
Solution
b. For the x-intercepts of the parabola, we solve the equation
using the quadratic formula with a =
2, b = 5, and c =
2.
We find
Thus, the x-intercepts of the parabola are 1/2 and 2.
2
2 5 2 0 x x + =
2
5 25 4( 2)( 2) 4 5 3
2 2( 2) 4
b b ac
x
a
= = =
Example
Given the quadratic function f(x) =
2x
2
+ 5x 2
a. Find the vertex of the parabola.
b. Find the x-intercepts (if any) of the parabola.
c. Sketch the parabola.
Solution
c. The sketch:
1 1 2
1
1
2
x
y
2
( ) 2 5 2 f x x x = +
Vertex
x-intercepts
1
2
5 9
,
4 8
| |
|
\ .
y-intercept
Some Economic Models
Peoples decision on how much to demand or purchase of a
given product depends on the price of the product:
The higher the price the less they want to buy of it.
A demand function p = d(x) can be used to describe this.
Some Economic Models
Similarly, firms decision on how much to supply or
produce of a product depends on the price of the product:
The higher the price, the more they want to produce of it.
A supply function p = s(x) can be used to describe this.
Some Economic Models
The interaction between demand and supply will ensure
the market settles to a market equilibrium:
This is the situation at which quantity demanded equals
quantity supplied.
Graphically, this situation occurs when the demand curve
and the supply curve intersect: where d(x) = s(x).
Applied Example: Supply and Demand
The demand function for a certain brand of bluetooth
wireless headset is given by
The corresponding supply function is given by
where p is the expressed in dollars and x is measured in
units of a thousand.
Find the equilibrium quantity and price.
2
( ) 0.025 0.5 60 p d x x x = = +
2
( ) 0.02 0.6 20 p s x x x = = + +
Applied Example: Supply and Demand
Solution
We solve the following system of equations:
Substituting the second equation into the first yields:
Thus, either x = 400/9 (but this is not possible), or x = 20.
So, the equilibrium quantity must be 20,000 headsets.
2
2
0.025 0.5 60
0.02 0.6 20
p x x
p x x
= +
= + +
( ) ( )
2 2
2
2
2
0.02 0.6 20 0.025 0.5 60
0.045 1.1 40 0
45 1100 40, 000 0
9 220 8, 000 0
9 400 20 0
x x x x
x x
x x
x x
x x
+ + = +
+ =
+ =
+ =
+ =
Applied Example: Supply and Demand
Solution
The equilibrium price is given by:
or $40 per headset.
( ) ( )
2
0.02 20 0.6 20 20 40 p = + + =
2.7
Functions and Mathematical Models
5 5 10 10 15 15 20 20 25 25 30 30
6 6
4 4
2 2
t t (years) (years)
y y ($trillion) ($trillion)
Mathematical Models
As we have seen, mathematics can be used to
solve real-world problems.
We will now discuss a few more examples of
real-world phenomena, such as:
The solvency of the U.S. Social Security
trust fund
Global warming
Mathematical Modeling
Regardless of the field from which the real-world problem
is drawn, the problem is analyzed using a process called
mathematical modeling.
The four steps in this process are:
Real-world problem
Mathematical
model
Solution of real-
world problem
Solution of
mathematical model
Formulate
Interpret
Solve
Test
Modeling With Polynomial Functions
A polynomial function of degree n is a function of the form
where n is a nonnegative integer and the numbers
a
0
, a
1
, . a
n
are constants called the coefficients of the
polynomial function.
Examples:
The function below is polynomial function of degree 5:
5 4 3 2
1
2
( ) 2 3 2 6 f x x x x x = + +
1 2
1 2 1 0
( ) ( 0)
n n
n n n
f x a x a x a x a x a a
= + + + + + =
Modeling With Polynomial Functions
A polynomial function of degree n is a function of the form
where n is a nonnegative integer and the numbers
a
0
, a
1
, . a
n
are constants called the coefficients of the
polynomial function.
Examples:
The function below is polynomial function of degree 3:
3 2
( ) 0.001 0.2 10 200 g x x x x = + +
1 2
1 2 1 0
( ) ( 0)
n n
n n n
f x a x a x a x a x a a
= + + + + + =
Applied Example: Global Warming
The increase in carbon dioxide (CO
2
) in the atmosphere is
a major cause of global warming.
Below is a table showing the average amount of CO
2
,
measured in parts per million volume (ppmv) for various
years from 1958 through 2007:
Year 1958 1970 1974 1978 1985 1991 1998 2003 2007
Amount 315 325 330 335 345 355 365 375 380
Applied Example: Global Warming
Below is a scatter plot associated with these data:
Year 1958 1970 1974 1978 1985 1991 1998 2003 2007
Amount 315 325 330 335 345 355 365 375 380
10 20 30 40 50
380
360
340
320
t (years)
y (ppmv)
Applied Example: Global Warming
A mathematical model giving the approximate amount of
CO
2
is given by:
Year 1958 1970 1974 1978 1985 1991 1998 2003 2007
Amount 315 325 330 335 345 355 365 375 380
10 20 30 40 50
380
360
340
320
t (years)
y (ppmv)
2
( ) 0.01076 0.8212 313.4 A t t t = + +
Applied Example: Global Warming
a. Use the model to estimate the average amount of atmospheric
CO
2
in 1980 (t = 23).
b. Assume that the trend continued and use the model to predict
the average amount of atmospheric CO
2
in 2010.
Year 1958 1970 1974 1978 1985 1991 1998 2003 2007
Amount 315 325 330 335 345 355 365 375 380
2
( ) 0.010716 0.8212 313.4 (1 50) A t t t t = + + s s
Applied Example: Global Warming
Solution
a. The average amount of atmospheric CO
2
in 1980 is given by
or approximately 338 ppmv.
b. Assuming that the trend will continue, the average amount of
atmospheric CO
2
in 2010 will be
Year 1958 1970 1974 1978 1985 1991 1998 2003 2007
Amount 315 325 330 335 345 355 365 375 380
( ) ( )
2
(23) 0.010716 23 0.8212 23 313.4 337.96 A = + + ~
( ) ( )
2
(53) 0.010716 53 0.8212 53 313.4 387.03 A = + + ~
2
( ) 0.010716 0.8212 313.4 (1 50) A t t t t = + + s s
Applied Example: Social Security Trust Fund
The projected assets of the Social Security trust fund (in
trillions of dollars) from 2008 through 2040 are given by:
The scatter plot associated with these data is:
Year 2008 2011 2014 2017 2020 2023 2026 2029 2032 2035 2038 2040
Assets 2.4 3.2 4.0 4.7 5.3 5.7 5.9 5.6 4.9 3.6 1.7 0
5 10 15 20 25 30
6
4
2
t (years)
y ($trillion)
The projected assets of the Social Security trust fund (in
trillions of dollars) from 2008 through 2040 are given by:
A mathematical model giving the approximate value of assets
in the trust fund (in trillions of dollars) is:
5 10 15 20 25 30
6
4
2
t (years)
y ($trillion)
4 3 2
( ) 0.00000324 0.000326 0.00342 0.254 2.4 A t t t t t = + + +
Year 2008 2011 2014 2017 2020 2023 2026 2029 2032 2035 2038 2040
Assets 2.4 3.2 4.0 4.7 5.3 5.7 5.9 5.6 4.9 3.6 1.7 0
Applied Example: Social Security Trust Fund
a. The first baby boomers will turn 65 in 2011. What will be the
assets of the Social Security trust fund at that time?
b. The last of the baby boomers will turn 65 in 2029. What will
the assets of the trust fund be at the time?
c. Use the graph of function A(t) to estimate the year in which
the current Social Security system will go broke.
4 3 2
( ) 0.00000324 0.000326 0.00342 0.254 2.4 A t t t t t = + + +
Year 2008 2011 2014 2017 2020 2023 2026 2029 2032 2035 2038 2040
Assets 2.4 3.2 4.0 4.7 5.3 5.7 5.9 5.6 4.9 3.6 1.7 0
Applied Example: Social Security Trust Fund
Solution
a. The assets of the Social Security fund in 2011 (t = 3) will be:
or approximately $3.18 trillion.
The assets of the Social Security fund in 2029 (t = 21) will be:
or approximately $5.59 trillion.
( ) ( ) ( ) ( )
4 3 2
(3) 0.00000324 3 0.000326 3 0.00342 3 0.254 3 2.4 3.18 A = + + + ~
( ) ( ) ( ) ( )
4 3 2
(21) 0.00000324 21 0.000326 21 0.00342 21 0.254 21 2.4 5.59 A = + + + ~
Year 2008 2011 2014 2017 2020 2023 2026 2029 2032 2035 2038 2040
Assets 2.4 3.2 4.0 4.7 5.3 5.7 5.9 5.6 4.9 3.6 1.7 0
4 3 2
( ) 0.00000324 0.000326 0.00342 0.254 2.4 A t t t t t = + + +
Applied Example: Social Security Trust Fund
Solution
b. The graph shows that function A crosses the t-axis at about
t = 32, suggesting the system will go broke by 2040:
5 10 15 20 25 30
6
4
2
y ($trillion)
Trust runs
out of funds
Year 2008 2011 2014 2017 2020 2023 2026 2029 2032 2035 2038 2040
Assets 2.4 3.2 4.0 4.7 5.3 5.7 5.9 5.6 4.9 3.6 1.7 0
4 3 2
( ) 0.00000324 0.000326 0.00342 0.254 2.4 A t t t t t = + + +
t (years)
Applied Example: Social Security Trust Fund
Rational and Power Functions
A rational function is simply the quotient of two
polynomials.
In general, a rational function has the form
where f(x) and g(x) are polynomial functions.
Since the division by zero is not allowed, we conclude that
the domain of a rational function is the set of all real
numbers except the zeros of g (the roots of the equation
g(x) = 0)
( )
( )
( )
f x
R x
g x
=
Rational and Power Functions
Examples of rational functions:
3 2
3 1
( )
2
x x x
F x
x
+ +
=
2
2
1
( )
1
x
G x
x
+
=
Rational and Power Functions
Functions of the form
where r is any real number, are called power functions.
We encountered examples of power functions earlier in
our work.
Examples of power functions:
1/2 2
2
1
( ) ( ) and f x x x g x x
x
= = = =
( )
r
f x x =
Rational and Power Functions
Many functions involve combinations of rational and
power functions.
Examples:
2
2
2
1/2
2 3/2
1
( )
1
( ) 3 4
1
( ) (1 2 )
( 2)
x
f x
x
g x x x
h x x
x
=
+
= +
= + +
+
Applied Example: Driving Costs
A study of driving costs based on a 2007 medium-sized
sedan found the following average costs (car payments,
gas, insurance, upkeep, and depreciation), measured in
cents per mile:
A mathematical model giving the average cost in cents per
mile is:
where x (in thousands) denotes the number of miles the car
is driven in 1 year.
Miles/year, x 5000 10,000 15,000 20,000
Cost/mile, y () 83.8 62.9 52.2 47.1
0.42
164.8
( ) C x
x
=
Applied Example: Driving Costs
Below is the scatter plot associated with this data:
0.42
164.8
( ) C x
x
=
5 10 15 20 25
140
120
100
80
60
40
20
x (1000 miles/year)
y ()
C(x)
Miles/year, x 5000 10,000 15,000 20,000
Cost/mile, y () 83.8 62.9 52.2 47.1
Applied Example: Driving Costs
Using this model, estimate the average cost of driving a
2007 medium-sized sedan 8,000 miles per year and 18,000
miles per year.
Solution
The average cost for driving a car 8,000 miles per year is
or approximately 68.8/mile.
0.42
164.8
( ) C x
x
=
( )
0.42
164.8
(8) 68.81
8
C = ~
Miles/year, x 5000 10,000 15,000 20,000
Cost/mile, y () 83.8 62.9 52.2 47.1
Applied Example: Driving Costs
Using this model, estimate the average cost of driving a
2007 medium-sized sedan 8,000 miles per year and 18,000
miles per year.
Solution
The average cost for driving a car 18,000 miles per year is
or approximately 48.95/mile.
0.42
164.8
( ) C x
x
=
( )
0.42
164.8
(18) 48.95
18
C = ~
Miles/year, x 5000 10,000 15,000 20,000
Cost/mile, y () 83.8 62.9 52.2 47.1
Constructing Mathematical Models
Some mathematical models can be constructed using
elementary geometric and algebraic arguments.
Guidelines for constructing mathematical models:
1. Assign a letter to each variable mentioned in the
problem. If appropriate, draw and label a figure.
2. Find an expression for the quantity sought.
3. Use the conditions given in the problem to write
the quantity sought as a function f of one variable.
Note any restrictions to be placed on the domain
of f by the nature of the problem.
Applied Example: Enclosing an Area
The owner of the Rancho Los Feliz has 3000 yards of
fencing with which to enclose a rectangular piece of
grazing land along the straight portion of a river.
Fencing is not required along the river.
Letting x denote the width of the rectangle, find a function
f in the variable x giving the area of the grazing land if she
uses all of the fencing.
Applied Example: Enclosing an Area
Solution
This information was given:
The area of the rectangular grazing land is A = xy.
The amount of fencing is 2x + y which must equal 3000
(to use all the fencing), so:
2x + y = 3000
Solving for y we get:
y = 3000 2x
Substituting this value of y into the expression for A gives:
A = x(3000 2x) = 3000x 2x
2
Finally, x and y represent distances, so they must be
nonnegative, so x > 0 and y = 3000 2x > 0 (or x s 1500).
Thus, the required function is:
f(x) = 3000x 2x
2
(0 s x s 1500)
Applied Example: Charter-Flight Revenue
If exactly 200 people sign up for a charter flight, Leisure
World Travel Agency charges $300 per person.
However, if more than 200 people sign up for the flight
(assume this is the case), then each fare is reduced by $1
for each additional person.
Letting x denote the number of passengers above 200, find
a function giving the revenue realized by the company.
Applied Example: Charter-Flight Revenue
Solution
This information was given.
If there are x passengers above 200, then the number of
passengers signing up for the flight is 200 + x.
The fare will be (300 x) dollars per passenger.
The revenue will be
R = (200 + x)(300 x)
=
x
2
+ 100x + 60,000
The quantities must be positive, so x > 0 and 300 x > 0
(or x s 300).
So the required function is:
f(x) =
x
2
+ 100x + 60,000 (0 s x s 300)
End of
Chapter
You might also like
- Exponential and Logarithmic FunctionsDocument20 pagesExponential and Logarithmic FunctionsKen AguilaNo ratings yet
- 3.1 Exponential Functions: Homework - PG 384 (1-45 Multiples of 3)Document25 pages3.1 Exponential Functions: Homework - PG 384 (1-45 Multiples of 3)cg5466No ratings yet
- Precalculus: The Limit of A FunctionDocument151 pagesPrecalculus: The Limit of A FunctionMay AbadNo ratings yet
- 3.0 Conic Sections Ellipses FCIT CompatDocument29 pages3.0 Conic Sections Ellipses FCIT CompatMykhaela Louize Gumban100% (1)
- Lesson 5 Permutation and CombinationsDocument40 pagesLesson 5 Permutation and Combinationsgela tinNo ratings yet
- Virtual Manipulatives in Mathematics EducationDocument7 pagesVirtual Manipulatives in Mathematics EducationCrystal WongNo ratings yet
- Learning Activity Sheets-Pre Cal - (Week 1)Document2 pagesLearning Activity Sheets-Pre Cal - (Week 1)Dominic Dalton CalingNo ratings yet
- 3.3 Graphs of Inverse FunctionsDocument31 pages3.3 Graphs of Inverse FunctionsAthinaNo ratings yet
- Conic SectionsDocument35 pagesConic SectionsGina Fe S. LegaspiNo ratings yet
- Circles Worksheet Day #1: (Hint: Find The Coordinates of The Center First)Document5 pagesCircles Worksheet Day #1: (Hint: Find The Coordinates of The Center First)satyam seetaramNo ratings yet
- Mutually Exclusive Events: Mutually Exclusive: Can't Happen at The Same TimeDocument5 pagesMutually Exclusive Events: Mutually Exclusive: Can't Happen at The Same TimeReygie Fabriga100% (1)
- Conic Sections Project 2Document1 pageConic Sections Project 2Shunshun Watermelon YanNo ratings yet
- 1 - Limits of Functions - DefinitionDocument22 pages1 - Limits of Functions - DefinitionRamon Jonathan Sapalaran100% (1)
- Function 3 (Inverse and Composite Function)Document19 pagesFunction 3 (Inverse and Composite Function)Ilham ShoyoNo ratings yet
- 02 - Rational InequalitiesDocument2 pages02 - Rational InequalitiesMahmoud Abdel-SalamNo ratings yet
- Lesson 7 Division of PolynomialsDocument26 pagesLesson 7 Division of PolynomialsHazel QuilalaNo ratings yet
- Competencies: Redgie G. UbayDocument3 pagesCompetencies: Redgie G. UbayRed Zye UbayNo ratings yet
- Mathematics Essential Learning Competencies Teaching-Learning Resources General Mathematics (Grade 11)Document28 pagesMathematics Essential Learning Competencies Teaching-Learning Resources General Mathematics (Grade 11)Monalisa Garcia BasañesNo ratings yet
- I. Illustrate The Tangent Line To The Graph of A Function at A Given PointDocument5 pagesI. Illustrate The Tangent Line To The Graph of A Function at A Given Pointrandom potatoNo ratings yet
- Lesson 8 Graphing Rational FunctionsDocument40 pagesLesson 8 Graphing Rational FunctionsCarbon CopyNo ratings yet
- Grade 9 Linear Equations in Two Variables CADocument10 pagesGrade 9 Linear Equations in Two Variables CAkuta100% (1)
- Warm Up Lesson Presentation Lesson Quiz: Holt Mcdougal Algebra 2 Holt Algebra 2 Holt Mcdougal Algebra 2Document34 pagesWarm Up Lesson Presentation Lesson Quiz: Holt Mcdougal Algebra 2 Holt Algebra 2 Holt Mcdougal Algebra 2Janseen Datuin JunioNo ratings yet
- FS GM Lesson PlanDocument12 pagesFS GM Lesson PlancrisnaNo ratings yet
- Piecewise Evaluation of Function ExercisesDocument19 pagesPiecewise Evaluation of Function ExercisesRowellyn Ilagan MaasNo ratings yet
- Calculus 1Document101 pagesCalculus 1mgandeviaNo ratings yet
- 1.5 Functions - Concepts - PiecewiseDocument18 pages1.5 Functions - Concepts - PiecewiseKhent Mhar AlborNo ratings yet
- 8 Graphing Rational FunctionsDocument9 pages8 Graphing Rational Functionszin GuevarraNo ratings yet
- Sequences: Grade 10 MathematicsDocument18 pagesSequences: Grade 10 MathematicsRemalyn Quinay CasemNo ratings yet
- Systems of Linear Equation in Two VariablesDocument8 pagesSystems of Linear Equation in Two VariablesEden Hannah Rensulat AnsingNo ratings yet
- Rules of Derivative PDFDocument28 pagesRules of Derivative PDFAriel Clopino PiolNo ratings yet
- 5.2 Ellipse and HyperbolaDocument18 pages5.2 Ellipse and HyperbolaJessy OeungNo ratings yet
- Introduction To Quadratic FunctionsDocument41 pagesIntroduction To Quadratic FunctionsLeah Mae OrtizNo ratings yet
- Multiple Choice Exam ReviewDocument20 pagesMultiple Choice Exam ReviewLJames SacuezaNo ratings yet
- TrigonometryDocument28 pagesTrigonometryDexter AhamedNo ratings yet
- Basic Calculus Teachers GuideDocument328 pagesBasic Calculus Teachers GuideDarren CalabiaNo ratings yet
- Exponents Scientific NotationDocument10 pagesExponents Scientific NotationhevelascoNo ratings yet
- Trigonometry Project Information SheetDocument7 pagesTrigonometry Project Information Sheetapi-261139685No ratings yet
- Section 3.8-3.10 Domain and Range Practice WorksheetDocument3 pagesSection 3.8-3.10 Domain and Range Practice WorksheetRodion Romanovich RaskolnikovNo ratings yet
- Significant Figures and Scientific NotationDocument28 pagesSignificant Figures and Scientific NotationLance De VeraNo ratings yet
- Exponential FunctionDocument27 pagesExponential FunctionSheena SheenNo ratings yet
- 8) C2 Graphs of Trigonometric FunctionsDocument27 pages8) C2 Graphs of Trigonometric FunctionsAhmed KhalilNo ratings yet
- Math10 q1 Mod3 Geometric Sequence and Geometric Means Ricky Landocan Bgo v2Document19 pagesMath10 q1 Mod3 Geometric Sequence and Geometric Means Ricky Landocan Bgo v2Roger KhanNo ratings yet
- Lesson 13 - Exponential Functions, Equations &Document7 pagesLesson 13 - Exponential Functions, Equations &Fretchie Anne C. LauroNo ratings yet
- Domain, Range, CodomainDocument6 pagesDomain, Range, CodomainKez MaxNo ratings yet
- Multiple Choice: Read Each Item Carefully. Write The Letter of The Best Answer in The Blank Provided For Each ItemDocument2 pagesMultiple Choice: Read Each Item Carefully. Write The Letter of The Best Answer in The Blank Provided For Each ItemCher GlenNo ratings yet
- Division of PolynomialsDocument25 pagesDivision of Polynomialsaleli jumaquioNo ratings yet
- Systems of Nonlinear EquationsDocument15 pagesSystems of Nonlinear EquationsClain ManalastasNo ratings yet
- The Ellipse: Analytic Geometry Section 3.3Document28 pagesThe Ellipse: Analytic Geometry Section 3.3Mohamed AbdirahmanNo ratings yet
- Graphs of Rational FunctionsDocument27 pagesGraphs of Rational FunctionsJimmy MagundayaoNo ratings yet
- Chapter 6 - Ratio and ProportionDocument7 pagesChapter 6 - Ratio and ProportionnbhaNo ratings yet
- Circular Permutation: What Is A Permutation?Document3 pagesCircular Permutation: What Is A Permutation?Jomar PajilaNo ratings yet
- Ppt-Venn Diagram and Set Operations - Part 1Document28 pagesPpt-Venn Diagram and Set Operations - Part 1Jonjon Marcos100% (2)
- LESSON 2 - Solving Quadratic Equations by Extracting Square RootsDocument4 pagesLESSON 2 - Solving Quadratic Equations by Extracting Square RootsMark Anthony CarlosNo ratings yet
- Simple Interest Worksheet 2Document2 pagesSimple Interest Worksheet 2A.BensonNo ratings yet
- Polynomial FunctionDocument6 pagesPolynomial FunctionYanyan Lapasaran PalecNo ratings yet
- Composite Functions: General Mathematics (Cor 005)Document15 pagesComposite Functions: General Mathematics (Cor 005)Rinoa Caye Villa-abrilleNo ratings yet
- Grade 9 Module 1Document16 pagesGrade 9 Module 1Gwaps Gabi100% (2)
- Chapter 2Document148 pagesChapter 2ehsansphNo ratings yet
- Mathematics Short Note For Grade 10Document4 pagesMathematics Short Note For Grade 10darseziyad34No ratings yet
- Third Quarter ActivityDocument39 pagesThird Quarter Activityeunica_dolojanNo ratings yet
- What Drives Systemic Bank Risk in EuropeDocument23 pagesWhat Drives Systemic Bank Risk in Europeayadi_ezer6795No ratings yet
- Risk Generating Industries For European Stock MarketsDocument14 pagesRisk Generating Industries For European Stock Marketsayadi_ezer6795No ratings yet
- M01 Rejda 6117643 11 Rmi C01Document15 pagesM01 Rejda 6117643 11 Rmi C01ayadi_ezer6795No ratings yet
- Fin118 Unit 9Document25 pagesFin118 Unit 9ayadi_ezer6795No ratings yet
- Financial Mathematics Course FIN 118 Unit Course 10 Number Unit Ordinary Annuity Annuity Due Unit SubjectDocument26 pagesFinancial Mathematics Course FIN 118 Unit Course 10 Number Unit Ordinary Annuity Annuity Due Unit Subjectayadi_ezer6795No ratings yet
- FIN118 Unit 12Document22 pagesFIN118 Unit 12ayadi_ezer6795No ratings yet
- Financial Mathematics Course FIN 118 Unit Course 7 Number Unit Sequences & Series Unit SubjectDocument27 pagesFinancial Mathematics Course FIN 118 Unit Course 7 Number Unit Sequences & Series Unit Subjectayadi_ezer6795No ratings yet
- Financial Mathematics Course FIN 118 Unit Course 4 Number Unit Integral Calculus Unit SubjectDocument17 pagesFinancial Mathematics Course FIN 118 Unit Course 4 Number Unit Integral Calculus Unit Subjectayadi_ezer6795No ratings yet
- Financial Mathematics Course FIN 118 Unit Course 6 Number Unit Applications of Matrices Unit SubjectDocument21 pagesFinancial Mathematics Course FIN 118 Unit Course 6 Number Unit Applications of Matrices Unit Subjectayadi_ezer6795No ratings yet
- Fin118 Unit 3Document27 pagesFin118 Unit 3ayadi_ezer6795No ratings yet
- Financial Mathematics Course FIN 118 Unit Course 5 Number Unit Matrices Unit SubjectDocument26 pagesFinancial Mathematics Course FIN 118 Unit Course 5 Number Unit Matrices Unit Subjectayadi_ezer6795No ratings yet
- Financial Mathematics Course FIN 118 Unit Course 1 Number Unit Linear Equations Quadratic Equations Unit SubjectDocument16 pagesFinancial Mathematics Course FIN 118 Unit Course 1 Number Unit Linear Equations Quadratic Equations Unit Subjectayadi_ezer6795No ratings yet
- Financial Mathematics Course FIN 118 Unit Course 2 Number Unit Limits of Function Continuity of Function Unit SubjectDocument35 pagesFinancial Mathematics Course FIN 118 Unit Course 2 Number Unit Limits of Function Continuity of Function Unit Subjectayadi_ezer6795No ratings yet
- Financial Mathematics Course FIN 118 Unit Course 0 Number Unit Introduction To The Course Unit SubjectDocument23 pagesFinancial Mathematics Course FIN 118 Unit Course 0 Number Unit Introduction To The Course Unit Subjectayadi_ezer6795No ratings yet
- Linear Algebra & MatricesDocument20 pagesLinear Algebra & Matriceskamayani_prNo ratings yet
- Business Mathematics Syllabus For 1st SemesterDocument2 pagesBusiness Mathematics Syllabus For 1st SemesterTejas RajNo ratings yet
- Sarang Math ProjectDocument10 pagesSarang Math Projectsarangmasal.1212No ratings yet
- Linear Algebra & Analytical GeometryDocument1 pageLinear Algebra & Analytical GeometryHamza ShahNo ratings yet
- IntegersDocument83 pagesIntegersAanya BhatnagarNo ratings yet
- CoshxDocument4 pagesCoshxMirellea AndurayNo ratings yet
- Quantum Source of Entropy For Black Holes Bombelli 1986Document11 pagesQuantum Source of Entropy For Black Holes Bombelli 1986pline11691No ratings yet
- CHAP TWO Worked Example Engineering Mecha-IDocument12 pagesCHAP TWO Worked Example Engineering Mecha-InvnrevNo ratings yet
- Fishers LDADocument47 pagesFishers LDABinduNo ratings yet
- Binomial Theorem: Full Marks 50 Choose The Correct Option Q1. (A) - . (B) - . (C) - . Q2. Q3Document1 pageBinomial Theorem: Full Marks 50 Choose The Correct Option Q1. (A) - . (B) - . (C) - . Q2. Q3CHP TSTPSNo ratings yet
- Sasakian Geometry (1e, 2008,620p, Oxford Mathematical Monographs) C.P.boyer, K.galicki - 0198564959Document620 pagesSasakian Geometry (1e, 2008,620p, Oxford Mathematical Monographs) C.P.boyer, K.galicki - 0198564959geworfen2013No ratings yet
- CVX USer GuideDocument99 pagesCVX USer GuideNakul PadalkarNo ratings yet
- Q1 Week 6 Polynomials Long DivisionDocument19 pagesQ1 Week 6 Polynomials Long DivisionsemicolonNo ratings yet
- Partial DerivativesDocument15 pagesPartial DerivativesAien Nurul AinNo ratings yet
- CEIC3000 Process Modelling and Analysis Week 1 Session 1, 2012Document17 pagesCEIC3000 Process Modelling and Analysis Week 1 Session 1, 2012Ben TanNo ratings yet
- Trigo FunctionsDocument17 pagesTrigo FunctionsNorhapidah Mohd SaadNo ratings yet
- Chapter 3Document8 pagesChapter 3ridhuanNo ratings yet
- Basic Mathematics CPPDocument5 pagesBasic Mathematics CPPiWareNo ratings yet
- Class 8th Ncert Maths PDFDocument8 pagesClass 8th Ncert Maths PDFSanjay BiradarNo ratings yet
- Finalexam 5e PracticeDocument21 pagesFinalexam 5e Practiceodette_7thNo ratings yet
- VectorsDocument55 pagesVectorsGeofrey KanenoNo ratings yet
- MTH 252 Section 4.4 Exercise 24: Justin Drawbert June 29, 2010Document2 pagesMTH 252 Section 4.4 Exercise 24: Justin Drawbert June 29, 2010Justin DrawbertNo ratings yet
- Hobsonajjustthemaths20021296smcetp PDFDocument1,296 pagesHobsonajjustthemaths20021296smcetp PDFAIvan DCam G0% (1)
- TQ q1 Math10 Diagnostic TestDocument5 pagesTQ q1 Math10 Diagnostic TestCherry Mae D. GrafiaNo ratings yet
- 2.5 FINAL REVIEW ASSIGNMENT Quadratic Functions and EquationsDocument5 pages2.5 FINAL REVIEW ASSIGNMENT Quadratic Functions and EquationsJana KatochNo ratings yet
- Vector and ScalarDocument51 pagesVector and ScalarMusic LastNo ratings yet
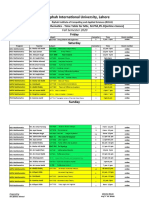
- Riphah International University, Lahore: Deparetment of Mathematics - Time Table For MSC, M.Phil, PH.D (Online Classes)Document2 pagesRiphah International University, Lahore: Deparetment of Mathematics - Time Table For MSC, M.Phil, PH.D (Online Classes)Anam BilqeesNo ratings yet
- 0 Arla18: 1Ä.B - 0 IblDocument7 pages0 Arla18: 1Ä.B - 0 IblNaman MishraNo ratings yet
- Tensor Calculus KayDocument238 pagesTensor Calculus KayNoa Noa Rey100% (9)